The Central Limit Theorem for Sample Means (Averages)

Suppose X is a random variable with a distribution that may be known or unknown (it can be any distribution). Using a subscript that matches the random variable, suppose:

If you draw random samples of size n, then as n increases, the random variable

\bar{X}

The central limit theorem for sample means says that if you keep drawing larger and larger samples (such as rolling one, two, five, and finally, ten dice) and calculating their means, the sample means form their own normal distribution (the sampling distribution). The normal distribution has the same mean as the original distribution and a variance that equals the original variance divided by the sample size. Standard deviation is the square root of variance, so the standard deviation of the sampling distribution is the standard deviation of the original distribution divided by the square root of n. The variable n is the number of values that are averaged together, not the number of times the experiment is done.

To put it more formally, if you draw random samples of size n, the distribution of the random variable

\bar{X}

, which consists of sample means, is called the sampling distribution of the mean. The sampling distribution of the mean approaches a normal distribution as n, the sample size, increases.

has a different z-score associated with it from that of the random variable X. The mean

\bar{x}

To find probabilities for means on the calculator, follow these steps.

2nd DISTR* * *

2:normalcdf

n o r m a l c d f (l o w e r v a l u e o f t h e a r e a, u p p e r v a l u e o f t h e a r e a, m e a n, \frac{s t a n d a r d d e v i a t i o n}{\sqrt{s a m p l e s i z e}})

where:

mean is the mean of the original distribution
standard deviation is the standard deviation of the original distribution
sample size = n

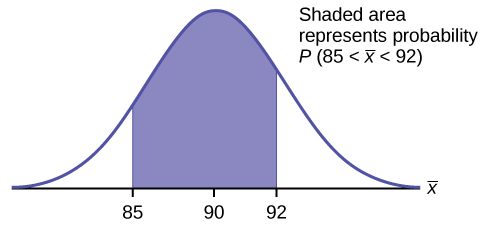
An unknown distribution has a mean of 90 and a standard deviation of 15. Samples of size n = 25 are drawn randomly from the population.

a. Find the probability that the sample mean is between 85 and 92.

a. Let X = one value from the original unknown population. The probability question asks you to find a probability for the sample mean.

Let $\bar{X}$

= the mean of a sample of size 25. Since μ_X = 90, σ_X = 15, and n = 25,

\bar{X}

~ N $(90, \frac{15}{\sqrt{25}})$

Find P(85 < $\bar{x}$

< 92). Draw a graph.

P(85 < $\bar{x}$

< 92) = 0.6997

The probability that the sample mean is between 85 and 92 is 0.6997.

This is a normal distribution curve. The peak of the curve coincides with the point 90 on the horizontal axis. The points 85 and 92 are labeled on the axis. Vertical lines are drawn from these points to the curve and the area between the lines is shaded. The shaded region represents the probability that 85 < x < 92. {:}

normalcdf(lower value, upper value, mean, standard error of the mean)

The parameter list is abbreviated (lower value, upper value, μ, $\frac{σ}{\sqrt{n}}$

)

normalcdf(85,92,90, $\frac{15}{\sqrt{25}}$

) = 0.6997

b. Find the value that is two standard deviations above the expected value, 90, of the sample mean.

b. To find the value that is two standard deviations above the expected value 90, use the formula:

value = μ_x + (#ofTSDEVs) $(\frac{σ_{x}}{\sqrt{n}})$

value = 90 + 2 $(\frac{15}{\sqrt{25}})$

= 96

The value that is two standard deviations above the expected value is 96.

The standard error of the mean is $\frac{σ x}{\sqrt{n}}$

= $\frac{15}{\sqrt{25}}$

= 3. Recall that the standard error of the mean is a description of how far (on average) that the sample mean will be from the population mean in repeated simple random samples of size n.

The length of time, in hours, it takes an “over 40” group of people to play one soccer match is normally distributed with a mean of two hours and a standard deviation of 0.5 hours. A sample of size n = 50 is drawn randomly from the population. Find the probability that the sample mean is between 1.8 hours and 2.3 hours.

Let X = the time, in hours, it takes to play one soccer match.

The probability question asks you to find a probability for the sample mean time, in hours, it takes to play one soccer match.

Let $\bar{X}$

= the mean time, in hours, it takes to play one soccer match.

If μ_X = _________, σ_X = __________, and n = ___________, then X ~ N(______, ______) by the central limit theorem for means.

μ_X = 2, σ_X = 0.5, n = 50, and X ~ N $(2, \frac{0.5}{\sqrt{50}})$

Find P(1.8 < $\bar{x}$

< 2.3). Draw a graph.

P(1.8 < $\bar{x}$

< 2.3) = 0.9977

normalcdf $(1. 8,2 .3,2, \frac{.5}{\sqrt{50}})$

= 0.9977

The probability that the mean time is between 1.8 hours and 2.3 hours is 0.9977.

To find percentiles for means on the calculator, follow these steps.

2^nd DIStR * * *

3:invNorm

k = invNorm $(area to the left of k, mean, \frac{s t a n d a r d d e v i a t i o n}{\sqrt{s a m p l e s i z e}})$

where:

k = the k^th percentile
mean is the mean of the original distribution
standard deviation is the standard deviation of the original distribution
sample size = n

In a recent study reported Oct. 29, 2012 on the Flurry Blog, the mean age of tablet users is 34 years. Suppose the standard deviation is 15 years. Take a sample of size n = 100.

What are the mean and standard deviation for the sample mean ages of tablet users?
What does the distribution look like?
Find the probability that the sample mean age is more than 30 years (the reported mean age of tablet users in this particular study).
Find the 95^th percentile for the sample mean age (to one decimal place).

Since the sample mean tends to target the population mean, we have μ_χ = μ = 34. The sample standard deviation is given by σ_χ = $\frac{σ}{\sqrt{n}}$
=
$\frac{15}{\sqrt{100}}$
=
$\frac{15}{10}$
= 1.5
The central limit theorem states that for large sample sizes(n), the sampling distribution will be approximately normal.
The probability that the sample mean age is more than 30 is given by P(Χ > 30) = normalcdf(30,E99,34,1.5) = 0.9962
Let k = the 95^th percentile.

k = invNorm
$(0. 95,34, \frac{15}{\sqrt{100}})$
= 36.5

Try It

In an article on Flurry Blog, a gaming marketing gap for men between the ages of 30 and 40 is identified. You are researching a startup game targeted at the 35-year-old demographic. Your idea is to develop a strategy game that can be played by men from their late 20s through their late 30s. Based on the article’s data, industry research shows that the average strategy player is 28 years old with a standard deviation of 4.8 years. You take a sample of 100 randomly selected gamers. If your target market is 29- to 35-year-olds, should you continue with your development strategy?

References

Baran, Daya. “20 Percent of Americans Have Never Used Email.”WebGuild, 2010. Available online at http://www.webguild.org/20080519/20-percent-of-americans-have-never-used-email (accessed May 17, 2013).

Data from The Flurry Blog, 2013. Available online at http://blog.flurry.com (accessed May 17, 2013).

Chapter Review

In a population whose distribution may be known or unknown, if the size (n) of samples is sufficiently large, the distribution of the sample means will be approximately normal. The mean of the sample means will equal the population mean. The standard deviation of the distribution of the sample means, called the standard error of the mean, is equal to the population standard deviation divided by the square root of the sample size (n).

Formula Review

Central Limit Theorem for Sample Means z-score and standard error of the mean:

z = \frac{\bar{x} - μ_{x}}{(\frac{σ_{x}}{\sqrt{n}})}

Use the following information to answer the next six exercises: Yoonie is a personnel manager in a large corporation. Each month she must review 16 of the employees. From past experience, she has found that the reviews take her approximately four hours each to do with a population standard deviation of 1.2 hours. Let Χ be the random variable representing the time it takes her to complete one review. Assume Χ is normally distributed. Let $\bar{X}$

be the random variable representing the mean time to complete the 16 reviews. Assume that the 16 reviews represent a random set of reviews.

What is the mean, standard deviation, and sample size?

mean = 4 hours; standard deviation = 1.2 hours; sample size = 16

Complete the distributions.

X ~ \_\_\_\_\_(\_\_\_\_\_,\_\_\_\_\_)
$\bar{X}$
~ \_\_\_\_\_(\_\_\_\_\_,\_\_\_\_\_)

Find the probability that one review will take Yoonie from 3.5 to 4.25 hours. Sketch the graph, labeling and scaling the horizontal axis. Shade the region corresponding to the probability.

{:}
P(________ < x < ________) = _______

a. Check student’s solution.* * *

b. 3.5, 4.25, 0.2441

Find the probability that the mean of a month’s reviews will take Yoonie from 3.5 to 4.25 hrs. Sketch the graph, labeling and scaling the horizontal axis. Shade the region corresponding to the probability.

{:}
P(\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_) = \_\_\_\_\_\_\_

What causes the probabilities in [link] and [link] to be different?

The fact that the two distributions are different accounts for the different probabilities.

Find the 95^th percentile for the mean time to complete one month's reviews. Sketch the graph.

{:}
The 95^th Percentile =\_\_\_\_\_\_\_\_\_\_\_\_

Homework

Previously, De Anza statistics students estimated that the amount of change daytime statistics students carry is exponentially distributed with a mean of $0.88. Suppose that we randomly pick 25 daytime statistics students.

In words, Χ = ____________
Χ ~ _____(_____,_____)
In words, $\bar{X}$
= ____________
$\bar{X}$
~ ______ (______, ______)
Find the probability that an individual had between $0.80 and $1.00. Graph the situation, and shade in the area to be determined.
Find the probability that the average of the 25 students was between $0.80 and $1.00. Graph the situation, and shade in the area to be determined.
Explain why there is a difference in part e and part f.

Χ = amount of change students carry
Χ ~ E(0.88, 0.88)
$\bar{X}$
= average amount of change carried by a sample of 25 sstudents.
$\bar{X}$
~ N(0.88, 0.176)
0.0819
0.1882
The distributions are different. Part a is exponential and part b is normal.

Suppose that the distance of fly balls hit to the outfield (in baseball) is normally distributed with a mean of 250 feet and a standard deviation of 50 feet. We randomly sample 49 fly balls.

If $\bar{X}$
= average distance in feet for 49 fly balls, then
$\bar{X}$
~ \_\_\_\_\_\_\_(\_\_\_\_\_\_\_,\_\_\_\_\_\_\_)
What is the probability that the 49 balls traveled an average of less than 240 feet? Sketch the graph. Scale the horizontal axis for $\bar{X}$
. Shade the region corresponding to the probability. Find the probability.
Find the 80^th percentile of the distribution of the average of 49 fly balls.

According to the Internal Revenue Service, the average length of time for an individual to complete (keep records for, learn, prepare, copy, assemble, and send) IRS Form 1040 is 10.53 hours (without any attached schedules). The distribution is unknown. Let us assume that the standard deviation is two hours. Suppose we randomly sample 36 taxpayers.

In words, Χ = _____________
In words, $\bar{X}$
= _____________
$\bar{X}$
~ _____(_____,_____)
Would you be surprised if the 36 taxpayers finished their Form 1040s in an average of more than 12 hours? Explain why or why not in complete sentences.
Would you be surprised if one taxpayer finished his or her Form 1040 in more than 12 hours? In a complete sentence, explain why.

length of time for an individual to complete IRS form 1040, in hours.
mean length of time for a sample of 36 taxpayers to complete IRS form 1040, in hours.
N $(10 .53, \frac{1}{3})$
Yes. I would be surprised, because the probability is almost 0.
No. I would not be totally surprised because the probability is 0.2312

Suppose that a category of world-class runners are known to run a marathon (26 miles) in an average of 145 minutes with a standard deviation of 14 minutes. Consider 49 of the races. Let $\bar{X}$

the average of the 49 races.

$\bar{X}$
~ \_\_\_\_\_(\_\_\_\_\_,\_\_\_\_\_)
Find the probability that the runner will average between 142 and 146 minutes in these 49 marathons.
Find the 80^th percentile for the average of these 49 marathons.
Find the median of the average running times.

The length of songs in a collector’s iTunes album collection is uniformly distributed from two to 3.5 minutes. Suppose we randomly pick five albums from the collection. There are a total of 43 songs on the five albums.

In words, Χ = _________
Χ ~ _____________
In words, $\bar{X}$
= _____________
$\bar{X}$
~ _____(_____,_____)
Find the first quartile for the average song length, $\bar{X}$
.
The IQR (interquartile range) for the average song length, $\bar{X}$
, is from ___ - ___.

the length of a song, in minutes, in the collection
U(2, 3.5)
the average length, in minutes, of the songs from a sample of five albums from the collection
N(2.75, 0.0660)
2.71 minutes
0.09 minutes

Determine which of the following are true and which are false. Then, in complete sentences, justify your answers.

When the sample size is large, the mean of $\bar{X}$
is approximately equal to the mean of Χ.
When the sample size is large, $\bar{X}$
is approximately normally distributed.
When the sample size is large, the standard deviation of $\bar{X}$
is approximately the same as the standard deviation of Χ.

True. The mean of a sampling distribution of the means is approximately the mean of the data distribution.
True. According to the Central Limit Theorem, the larger the sample, the closer the sampling distribution of the means becomes normal.
The standard deviation of the sampling distribution of the means will decrease making it approximately the same as the standard deviation of X as the sample size increases.

The percent of fat calories that a person in America consumes each day is normally distributed with a mean of about 36 and a standard deviation of about ten. Suppose that 16 individuals are randomly chosen. Let $\bar{X}$

= average percent of fat calories.

$\bar{X}$
~ \_\_\_\_\_\_(\_\_\_\_\_\_, \_\_\_\_\_\_)
For the group of 16, find the probability that the average percent of fat calories consumed is more than five. Graph the situation and shade in the area to be determined.
Find the first quartile for the average percent of fat calories.

The distribution of income in some Third World countries is considered wedge shaped (many very poor people, very few middle income people, and even fewer wealthy people). Suppose we pick a country with a wedge shaped distribution. Let the average salary be $2,000 per year with a standard deviation of $8,000. We randomly survey 1,000 residents of that country.

In words, Χ = _____________
In words, $\bar{X}$
= _____________
$\bar{X}$
~ _____(_____,_____)
How is it possible for the standard deviation to be greater than the average?
Why is it more likely that the average of the 1,000 residents will be from $2,000 to $2,100 than from $2,100 to $2,200?

X = the yearly income of someone in a third world country
the average salary from samples of 1,000 residents of a third world country
$\bar{X}$
∼ N
$(2000, \frac{8000}{\sqrt{1000}})$
Very wide differences in data values can have averages smaller than standard deviations.
The distribution of the sample mean will have higher probabilities closer to the population mean.

P(2000 <
$\bar{X}$
< 2100) = 0.1537

P(2100 <
$\bar{X}$
< 2200) = 0.1317

The cost of unleaded gasoline in the Bay Area once followed an unknown distribution with a mean of $4.59 and a standard deviation of $0.10. Sixteen gas stations from the Bay Area are randomly chosen. We are interested in the average cost of gasoline for the 16 gas stations. The distribution to use for the average cost of gasoline for the 16 gas stations is:

$\bar{X}$
~ N(4.59, 0.10)
$\bar{X}$
~ N
$(4 .59, \frac{0.10}{\sqrt{16}})$
$\bar{X}$
~ N
$(4 .59, \frac{16}{0.10})$
$\bar{X}$
~ N
$(4 .59, \frac{\sqrt{16}}{0.10})$

Glossary

Average: a number that describes the central tendency of the data; there are a number of specialized averages, including the arithmetic mean, weighted mean, median, mode, and geometric mean.

Central Limit Theorem

Given a random variable (RV) with known mean μ and known standard deviation, σ, we are sampling with size n, and we are interested in two new RVs: the sample mean,

\bar{X}

, and the sample sum, ΣΧ. If the size (n) of the sample is sufficiently large, then

\bar{X}

~ N(μ,

\frac{σ}{\sqrt{n}}

) and ΣΧ ~ N(nμ, (

\sqrt{n}

)(σ)). If the size (n) of the sample is sufficiently large, then the distribution of the sample means and the distribution of the sample sums will approximate a normal distributions regardless of the shape of the population. The mean of the sample means will equal the population mean, and the mean of the sample sums will equal n times the population mean. The standard deviation of the distribution of the sample means,

\frac{σ}{\sqrt{n}}

, is called the standard error of the mean.

Normal Distribution: a continuous random variable (RV) with pdf $f (x) = \frac{1}{σ \sqrt{2 π}} e^{\frac{- {(x - μ)}^{2}}{2 σ^{2}}}$
, where μ is the mean of the distribution and σ is the standard deviation; notation: Χ ~ N(μ, σ). If μ = 0 and σ = 1, the RV is called a standard normal distribution.

Standard Error of the Mean: the standard deviation of the distribution of the sample means, or $\frac{σ}{\sqrt{n}}$
.