Poisson Distribution · Statistics

The average number of loaves of bread put on a shelf in a bakery in a half-hour period is 12. Of interest is the number of loaves of bread put on the shelf in five minutes. The time interval of interest is five minutes. What is the probability that the number of loaves, selected randomly, put on the shelf in five minutes is three?

Let X = the number of loaves of bread put on the shelf in five minutes. If the average number of loaves put on the shelf in 30 minutes (half-hour) is 12, then the average number of loaves put on the shelf in five minutes is $(\frac{5}{30})$

(12) = 2 loaves of bread.

The probability question asks you to find P(x = 3).

A bank expects to receive six bad checks per day, on average. What is the probability of the bank getting fewer than five bad checks on any given day? Of interest is the number of checks the bank receives in one day, so the time interval of interest is one day. Let X = the number of bad checks the bank receives in one day. If the bank expects to receive six bad checks per day then the average is six checks per day. Write a mathematical statement for the probability question.

P(x < 5)

You notice that a news reporter says "uh," on average, two times per broadcast. What is the probability that the news reporter says "uh" more than two times per broadcast.

This is a Poisson problem because you are interested in knowing the number of times the news reporter says "uh" during a broadcast.* * *

a. What is the interval of interest?

a. one broadcast* * *

b. What is the average number of times the news reporter says “uh” during one broadcast?

b. 2* * *

c. Let X = ____________. What values does X take on?

c. Let X = the number of times the news reporter says “uh” during one broadcast. * * *

x = 0, 1, 2, 3, …* * *

d. The probability question is P(______).

d. P(x > 2)

Notation for the Poisson: P = Poisson Probability Distribution Function

Read this as "X is a random variable with a Poisson distribution." The parameter is μ (or λ); μ (or λ) = the mean for the interval of interest.

Leah's answering machine receives about six telephone calls between 8 a.m. and 10 a.m. What is the probability that Leah receives more than one call in the next 15 minutes?

Let X = the number of calls Leah receives in 15 minutes. (The interval of interest is 15 minutes or $\frac{1}{4}$

hour.)

x = 0, 1, 2, 3, …

If Leah receives, on the average, six telephone calls in two hours, and there are eight 15 minute intervals in two hours, then Leah receives

(\frac{1}{8})

(6) = 0.75 calls in 15 minutes, on average. So, μ = 0.75 for this problem.

X ~ P(0.75)

Find P(x > 1). P(x > 1) = 0.1734 (calculator or computer)

Press 1 – and then press 2^nd DISTR.
Arrow down to poissoncdf. Press ENTER.
Enter (.75,1).
The result is P(x > 1) = 0.1734.

Note

The TI calculators use λ (lambda) for the mean.

The probability that Leah receives more than one telephone call in the next 15 minutes is about 0.1734: * * *

P(x > 1) = 1 − poissoncdf(0.75, 1).

The graph of X ~ P(0.75) is:

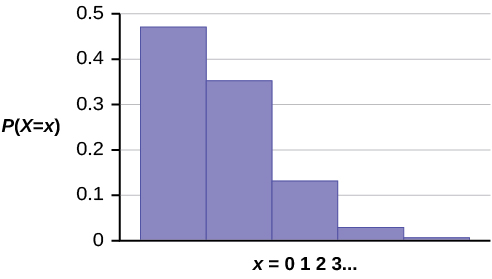This graphs shows a poisson probability distribution. It has 5 bars that decrease in height from left to right. The x-axis shows values in increments of 1 starting with 0, representing the number of calls Leah receives within 15 minutes. The y-axis ranges from 0 to 0.5 in increments of 0.1. {:}

The y-axis contains the probability of x where X = the number of calls in 15 minutes.

According to Baydin, an email management company, an email user gets, on average, 147 emails per day. Let X = the number of emails an email user receives per day. The discrete random variable X takes on the values x = 0, 1, 2 …. The random variable X has a Poisson distribution: X ~ P(147). The mean is 147 emails.

What is the probability that an email user receives exactly 160 emails per day?
What is the probability that an email user receives at most 160 emails per day?
What is the standard deviation?

P(x = 160) = poissonpdf(147, 160) ≈ 0.0180
P(x ≤ 160) = poissoncdf(147, 160) ≈ 0.8666
Standard Deviation = $σ = \sqrt{μ} = \sqrt{147} \approx 12.1244$

Try It

According to a recent poll by the Pew Internet Project, girls between the ages of 14 and 17 send an average of 187 text messages each day. Let X = the number of texts that a girl aged 14 to 17 sends per day. The discrete random variable X takes on the values x = 0, 1, 2 …. The random variable X has a Poisson distribution: X ~ P(187). The mean is 187 text messages.

What is the probability that a teen girl sends exactly 175 texts per day?
What is the probability that a teen girl sends at most 150 texts per day?
What is the standard deviation?

Text message users receive or send an average of 41.5 text messages per day.

How many text messages does a text message user receive or send per hour?
What is the probability that a text message user receives or sends two messages per hour?
What is the probability that a text message user receives or sends more than two messages per hour?

Let X = the number of texts that a user sends or receives in one hour. The average number of texts received per hour is $\frac{41.5}{24}$
≈ 1.7292.
X ~ P(1.7292), so P(x = 2) = poissonpdf(1.7292, 2) ≈ 0.2653
P(x > 2) = 1 – P(x ≤ 2) = 1 – poissoncdf(1.7292, 2) ≈ 1 – 0.7495 = 0.2505

On May 13, 2013, starting at 4:30 PM, the probability of low seismic activity for the next 48 hours in Alaska was reported as about 1.02%. Use this information for the next 200 days to find the probability that there will be low seismic activity in ten of the next 200 days. Use both the binomial and Poisson distributions to calculate the probabilities. Are they close?

Let X = the number of days with low seismic activity.

Using the binomial distribution:

P(x = 10) = binompdf(200, .0102, 10) ≈ 0.000039

Using the Poisson distribution:

Calculate μ = np = 200(0.0102) ≈ 2.04
P(x = 10) = poissonpdf(2.04, 10) ≈ 0.000045

We expect the approximation to be good because n is large (greater than 20) and p is small (less than 0.05). The results are close—both probabilities reported are almost 0.

References

“ATL Fact Sheet,” Department of Aviation at the Hartsfield-Jackson Atlanta International Airport, 2013. Available online at http://www.atlanta-airport.com/Airport/ATL/ATL\_FactSheet.aspx (accessed May 15, 2013).

Center for Disease Control and Prevention. “Teen Drivers: Fact Sheet,” Injury Prevention & Control: Motor Vehicle Safety, October 2, 2012. Available online at http://www.cdc.gov/Motorvehiclesafety/Teen\_Drivers/teendrivers\_factsheet.html (accessed May 15, 2013).

“Children and Childrearing,” Ministry of Health, Labour, and Welfare. Available online at http://www.mhlw.go.jp/english/policy/children/children-childrearing/index.html (accessed May 15, 2013).

“Eating Disorder Statistics,” South Carolina Department of Mental Health, 2006. Available online at http://www.state.sc.us/dmh/anorexia/statistics.htm (accessed May 15, 2013).

“Giving Birth in Manila: The maternity ward at the Dr Jose Fabella Memorial Hospital in Manila, the busiest in the Philippines, where there is an average of 60 births a day,” theguardian, 2013. Available online at http://www.theguardian.com/world/gallery/2011/jun/08/philippines-health#/?picture=375471900&index=2 (accessed May 15, 2013).

“How Americans Use Text Messaging,” Pew Internet, 2013. Available online at http://pewinternet.org/Reports/2011/Cell-Phone-Texting-2011/Main-Report.aspx (accessed May 15, 2013).

Lenhart, Amanda. “Teens, Smartphones & Testing: Texting volum is up while the frequency of voice calling is down. About one in four teens say they own smartphones,” Pew Internet, 2012. Available online at http://www.pewinternet.org/~/media/Files/Reports/2012/PIP\_Teens\_Smartphones\_and\_Texting.pdf (accessed May 15, 2013).

“One born every minute: the maternity unit where mothers are THREE to a bed,” MailOnline. Available online at http://www.dailymail.co.uk/news/article-2001422/Busiest-maternity-ward-planet-averages-60-babies-day-mothers-bed.html (accessed May 15, 2013).

Vanderkam, Laura. “Stop Checking Your Email, Now.” CNNMoney, 2013. Available online at http://management.fortune.cnn.com/2012/10/08/stop-checking-your-email-now/ (accessed May 15, 2013).

“World Earthquakes: Live Earthquake News and Highlights,” World Earthquakes, 2012. http://www.world-earthquakes.com/index.php?option=ethq\_prediction (accessed May 15, 2013).

Chapter Review

A Poisson probability distribution of a discrete random variable gives the probability of a number of events occurring in a fixed interval of time or space, if these events happen at a known average rate and independently of the time since the last event. The Poisson distribution may be used to approximate the binomial, if the probability of success is "small" (less than or equal to 0.05) and the number of trials is "large" (greater than or equal to 20).

Formula Review

X ~ P(μ) means that X has a Poisson probability distribution where X = the number of occurrences in the interval of interest.

When P(μ) is used to approximate a binomial distribution, μ = np where n represents the number of independent trials and p represents the probability of success in a single trial.

Use the following information to answer the next six exercises: On average, a clothing store gets 120 customers per day.

Assume the event occurs independently in any given day. Define the random variable X.

What values does X take on?

0, 1, 2, 3, 4, …

What is the probability of getting 150 customers in one day?

What is the probability of getting 35 customers in the first four hours? Assume the store is open 12 hours each day.

0.0485

What is the probability that the store will have more than 12 customers in the first hour?

What is the probability that the store will have fewer than 12 customers in the first two hours?

0.0214

Which type of distribution can the Poisson model be used to approximate? When would you do this?

Use the following information to answer the next six exercises: On average, eight teens in the U.S. die from motor vehicle injuries per day. As a result, states across the country are debating raising the driving age.

Assume the event occurs independently in any given day. In words, define the random variable X.

X = the number of U.S. teens who die from motor vehicle injuries per day.

X ~ \_\_\_\_\_(\_\_\_\_\_,\_\_\_\_\_)

What values does X take on?

0, 1, 2, 3, 4, …

For the given values of the random variable X, fill in the corresponding probabilities.

Is it likely that there will be no teens killed from motor vehicle injuries on any given day in the U.S? Justify your answer numerically.

Is it likely that there will be more than 20 teens killed from motor vehicle injuries on any given day in the U.S.? Justify your answer numerically.

HOMEWORK

The switchboard in a Minneapolis law office gets an average of 5.5 incoming phone calls during the noon hour on Mondays. Experience shows that the existing staff can handle up to six calls in an hour. Let X = the number of calls received at noon.

Find the mean and standard deviation of X.
What is the probability that the office receives at most six calls at noon on Monday?
Find the probability that the law office receives six calls at noon. What does this mean to the law office staff who get, on average, 5.5 incoming phone calls at noon?
What is the probability that the office receives more than eight calls at noon?

X ~ P(5.5); μ = 5.5; $σ = \sqrt{5.5}$
≈ 2.3452
P(x ≤ 6) = poissoncdf(5.5, 6) ≈ 0.6860
There is a 15.7% probability that the law staff will receive more calls than they can handle.
P(x > 8) = 1 – P(x ≤ 8) = 1 – poissoncdf(5.5, 8) ≈ 1 – 0.8944 = 0.1056

The maternity ward at Dr. Jose Fabella Memorial Hospital in Manila in the Philippines is one of the busiest in the world with an average of 60 births per day. Let X = the number of births in an hour.

Find the mean and standard deviation of X.
Sketch a graph of the probability distribution of X.
What is the probability that the maternity ward will deliver three babies in one hour?
What is the probability that the maternity ward will deliver at most three babies in one hour?
What is the probability that the maternity ward will deliver more than five babies in one hour?

A manufacturer of Christmas tree light bulbs knows that 3% of its bulbs are defective. Find the probability that a string of 100 lights contains at most four defective bulbs using both the binomial and Poisson distributions.

Let X = the number of defective bulbs in a string.

Using the Poisson distribution:

μ = np = 100(0.03) = 3
X ~ P(3)
P(x ≤ 4) = poissoncdf(3, 4) ≈ 0.8153

Using the binomial distribution:

X ~ B(100, 0.03)
P(x ≤ 4) = binomcdf(100, 0.03, 4) ≈ 0.8179

The Poisson approximation is very good—the difference between the probabilities is only 0.0026.

The average number of children a Spanish woman has in her lifetime is 1.47. Suppose that one Spanish woman is randomly chosen.

In words, define the Random Variable X.
List the values that X may take on.
Give the distribution of X. X ~ _____(_____,_____)
Find the probability that she has no children.
Find the probability that she has fewer children than the Spanish average.
Find the probability that she has more children than the Spanish average .

X = the number of children for a Spanish woman
0, 1, 2, 3,…
X ~ P(1.47)
0.2299
0.5679
0.4321

Fertile, female cats produce an average of three litters per year. Suppose that one fertile, female cat is randomly chosen. In one year, find the probability she produces:

In words, define the random variable X.
List the values that X may take on.
Give the distribution of X. X ~ \_\_\_\_\_\_\_
Find the probability that she has no litters in one year.
Find the probability that she has at least two litters in one year.
Find the probability that she has exactly three litters in one year.

The chance of having an extra fortune in a fortune cookie is about 3%. Given a bag of 144 fortune cookies, we are interested in the number of cookies with an extra fortune. Two distributions may be used to solve this problem, but only use one distribution to solve the problem.

In words, define the random variable X.
List the values that X may take on.
Give the distribution of X. X ~ _____(_____,_____)
How many cookies do we expect to have an extra fortune?
Find the probability that none of the cookies have an extra fortune.
Find the probability that more than three have an extra fortune.
As n increases, what happens involving the probabilities using the two distributions? Explain in complete sentences.

X = the number of fortune cookies that have an extra fortune
0, 1, 2, 3,… 144
X ~ B(144, 0.03) or P(4.32)
4.32
0.0124 or 0.0133
0.6300 or 0.6264
As n gets larger, the probabilities get closer together.

According to the South Carolina Department of Mental Health web site, for every 200 U.S. women, the average number who suffer from anorexia is one. Out of a randomly chosen group of 600 U.S. women determine the following.

In words, define the random variable X.
List the values that X may take on.
Give the distribution ofX. X ~ \_\_\_\_\_(\_\_\_\_\_,\_\_\_\_\_)
How many are expected to suffer from anorexia?
Find the probability that no one suffers from anorexia.
Find the probability that more than four suffer from anorexia.

The chance of an IRS audit for a tax return with over $25,000 in income is about 2% per year. Suppose that 100 people with tax returns over $25,000 are randomly picked. We are interested in the number of people audited in one year. Use a Poisson distribution to anwer the following questions.

In words, define the random variable X.
List the values that X may take on.
Give the distribution of X. X ~ _____(_____,_____)
How many are expected to be audited?
Find the probability that no one was audited.
Find the probability that at least three were audited.

X = the number of people audited in one year
0, 1, 2, …, 100
X ~ P(2)
2
0.1353
0.3233

Approximately 8% of students at a local high school participate in after-school sports all four years of high school. A group of 60 seniors is randomly chosen. Of interest is the number that participated in after-school sports all four years of high school.

In words, define the random variable X.
List the values that X may take on.
Give the distribution of X. X ~ \_\_\_\_\_(\_\_\_\_\_,\_\_\_\_\_)
How many seniors are expected to have participated in after-school sports all four years of high school?
Based on numerical values, would you be surprised if none of the seniors participated in after-school sports all four years of high school? Justify your answer numerically.
Based on numerical values, is it more likely that four or that five of the seniors participated in after-school sports all four years of high school? Justify your answer numerically.

On average, Pierre, an amateur chef, drops three pieces of egg shell into every two cake batters he makes. Suppose that you buy one of his cakes.

In words, define the random variable X.
List the values that X may take on.
Give the distribution of X. X ~ _____(_____,_____)
On average, how many pieces of egg shell do you expect to be in the cake?
What is the probability that there will not be any pieces of egg shell in the cake?
Let’s say that you buy one of Pierre’s cakes each week for six weeks. What is the probability that there will not be any egg shell in any of the cakes?
Based upon the average given for Pierre, is it possible for there to be seven pieces of shell in the cake? Why?

X = the number of shell pieces in one cake
0, 1, 2, 3,…
X ~ P(1.5)
1.5
0.2231
0.0001
Yes

Use the following information to answer the next two exercises: The average number of times per week that Mrs. Plum’s cats wake her up at night because they want to play is ten. We are interested in the number of times her cats wake her up each week.

Glossary

Poisson Probability Distribution

a discrete random variable (RV) that counts the number of times a certain event will occur in a specific interval; characteristics of the variable:

The probability that the event occurs in a given interval is the same for all intervals.
The events occur with a known mean and independently of the time since the last event.

The distribution is defined by the mean μ of the event in the interval. Notation: X ~ P(μ). The mean is μ = np. The standard deviation is

σ = \sqrt{μ}

. The probability of having exactly x successes in r trials is P(X = x ) =

(e^{- μ}) \frac{μ^{x}}{x!}

. The Poisson distribution is often used to approximate the binomial distribution, when n is “large” and p is “small” (a general rule is that n should be greater than or equal to 20 and p should be less than or equal to 0.05).