Finding Limits: Numerical and Graphical Approaches

In this section, you will:

Understand limit notation.
Find a limit using a graph.
Find a limit using a table.

Intuitively, we know what a limit is. A car can go only so fast and no faster. A trash can might hold 33 gallons and no more. It is natural for measured amounts to have limits. What, for instance, is the limit to the height of a woman? The tallest woman on record was Jinlian Zeng from China, who was 8 ft 1 in.¹ Is this the limit of the height to which women can grow? Perhaps not, but there is likely a limit that we might describe in inches if we were able to determine what it was.

To put it mathematically, the function whose input is a woman and whose output is a measured height in inches has a limit. In this section, we will examine numerical and graphical approaches to identifying limits.

Understanding Limit Notation

We have seen how a sequence can have a limit, a value that the sequence of terms moves toward as the nu mber of terms increases. For example, the terms of the sequence

1, \frac{1}{2}, \frac{1}{4}, \frac{1}{8} ...

gets closer and closer to 0. A sequence is one type of function, but functions that are not sequences can also have limits. We can describe the behavior of the function as the input values get close to a specific value. If the limit of a function $f (x) = L,$

then as the input $x$

gets closer and closer to $a,$

the output y-coordinate gets closer and closer to $L .$

We say that the output “approaches” $L .$

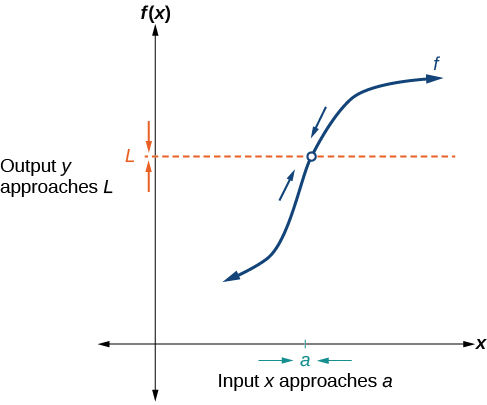
[link] provides a visual representation of the mathematical concept of limit. As the input value $x$

approaches $a,$

the output value $f (x)$

approaches $L .$

Graph representing how a function with a hole at (a, L) approaches a limit.

We write the equation of a limit as

\lim_{x \to a} f (x) = L .

This notation indicates that as $x$

approaches $a$

both from the left of $x = a$

and the right of $x = a,$

the output value approaches $L .$

Consider the function

f (x) = \frac{x^{2} - 6 x - 7}{x - 7} .

We can factor the function as shown.

\begin{array}{l} f (x) = \frac{(x - 7) (x + 1)}{x - 7} & Cancel like factors in numerator and denominator . \\ f (x) = x + 1, x \neq 7 & Simplify . \end{array}

Notice that $x$

cannot be 7, or we would be dividing by 0, so 7 is not in the domain of the original function. In order to avoid changing the function when we simplify, we set the same condition, $x \neq 7,$

for the simplified function. We can represent the function graphically as shown in [link].

Graph of an increasing function, f(x) = (x^2-6x-7)/(x-7), with a hole at (7, 8).

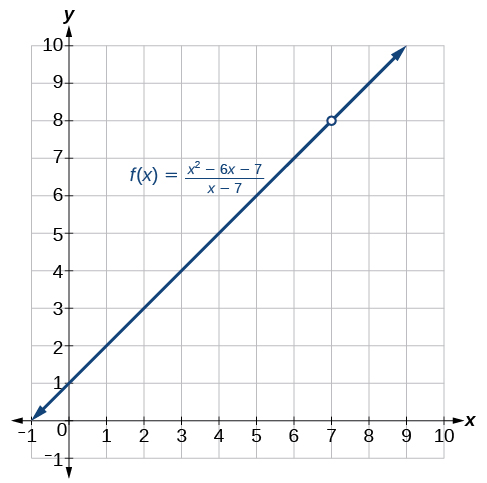
What happens at $x = 7$

is completely different from what happens at points close to $x = 7$

on either side. The notation

\lim_{x \to 7} f (x) = 8

indicates that as the input $x$

approaches 7 from either the left or the right, the output approaches 8. The output can get as close to 8 as we like if the input is sufficiently near 7.

What happens at $x = 7 ?$

When $x = 7,$

there is no corresponding output. We write this as

f (7) does not exist .

This notation indicates that 7 is not in the domain of the function. We had already indicated this when we wrote the function as

f (x) = x + 1, x \neq 7.

Notice that the limit of a function can exist even when $f (x)$

is not defined at $x = a .$

Much of our subsequent work will be determining limits of functions as $x$

nears $a,$

even though the output at $x = a$

does not exist.

The Limit of a Function

A quantity $L$

is the limit of a function $f (x)$

as $x$

approaches $a$

if, as the input values of $x$

approach $a$

(but do not equal $a),$

the corresponding output values of $f (x)$

get closer to $L .$

Note that the value of the limit is not affected by the output value of $f (x)$

at $a .$

Both $a$

and $L$

must be real numbers. We write it as

\lim_{x \to a} f (x) = L

Understanding the Limit of a Function

For the following limit, define $a, f (x),$

and $L .$

\lim_{x \to 2} (3 x + 5) = 11

First, we recognize the notation of a limit. If the limit exists, as $x$

approaches $a,$

we write

\lim_{x \to a} f (x) = L .

We are given

\lim_{x \to 2} (3 x + 5) = 11.

This means that $a = 2, f (x) = 3 x + 5, and L = 11.$

Analysis

Recall that $y = 3 x + 5$

is a line with no breaks. As the input values approach 2, the output values will get close to 11. This may be phrased with the equation $\lim_{x \to 2} (3 x + 5) = 11,$

which means that as $x$

nears 2 (but is not exactly 2), the output of the function $f (x) = 3 x + 5$

gets as close as we want to $3 (2) + 5,$

or 11, which is the limit $L,$

as we take values of $x$

sufficiently near 2 but not at $x = 2.$

For the following limit, define $a, f (x),$

and $L .$

\lim_{x \to 5} (2 x^{2} - 4) = 46

a = 5,

f (x) = 2 x^{2} - 4,

and $L = 46.$

Understanding Left-Hand Limits and Right-Hand Limits

We can approach the input of a function from either side of a value—from the left or the right. [link] shows the values of

f (x) = x + 1, x \neq 7

as described earlier and depicted in [link].

Table showing that f(x) approaches 8 from either side as x approaches 7 from either side.

Values described as “from the left” are less than the input value 7 and would therefore appear to the left of the value on a number line. The input values that approach 7 from the left in [link] are $6.9,$

6.99,

and $6.999.$

The corresponding outputs are $7.9, 7.99,$

and $7.999.$

These values are getting closer to 8. The limit of values of $f (x)$

as $x$

approaches from the left is known as the left-hand limit. For this function, 8 is the left-hand limit of the function $f (x) = x + 1, x \neq 7$

as $x$

approaches 7.

Values described as “from the right” are greater than the input value 7 and would therefore appear to the right of the value on a number line. The input values that approach 7 from the right in [link] are $7.1,$

7.01,

and $7.001.$

The corresponding outputs are $8.1,$

8.01,

and $8.001.$

These values are getting closer to 8. The limit of values of $f (x)$

as $x$

approaches from the right is known as the right-hand limit. For this function, 8 is also the right-hand limit of the function $f (x) = x + 1, x \neq 7$

as $x$

approaches 7.

[link] shows that we can get the output of the function within a distance of 0.1 from 8 by using an input within a distance of 0.1 from 7. In other words, we need an input $x$

within the interval $6.9 < x < 7.1$

to produce an output value of $f (x)$

within the interval $7.9 < f (x) < 8.1.$

We also see that we can get output values of $f (x)$

successively closer to 8 by selecting input values closer to 7. In fact, we can obtain output values within any specified interval if we choose appropriate input values.

[link] provides a visual representation of the left- and right-hand limits of the function. From the graph of $f (x),$

we observe the output can get infinitesimally close to $L = 8$

as $x$

approaches 7 from the left and as $x$

approaches 7 from the right.

To indicate the left-hand limit, we write

\lim_{x \to 7^{-}} f (x) = 8.

To indicate the right-hand limit, we write

\lim_{x \to 7^{+}} f (x) = 8.

Graph of the previous function explaining the function's limit at (7, 8)

Left- and Right-Hand Limits

The left-hand limit of a function $f (x)$

as $x$

approaches $a$

from the left is equal to $L,$

denoted by

\lim_{x \to a^{-}} f (x) = L .

The values of $f (x)$

can get as close to the limit $L$

as we like by taking values of $x$

sufficiently close to $a$

such that $x < a$

and $x \neq a .$

The right-hand limit of a function $f (x),$

as $x$

approaches $a$

from the right, is equal to $L,$

denoted by

\lim_{x \to a^{+}} f (x) = L .

The values of $f (x)$

can get as close to the limit $L$

as we like by taking values of $x$

sufficiently close to $a$

but greater than $a .$

Both $a$

and $L$

are real numbers.

Understanding Two-Sided Limits

In the previous example, the left-hand limit and right-hand limit as $x$

approaches $a$

are equal. If the left- and right-hand limits are equal, we say that the function $f (x)$

has a two-sided limit as $x$

approaches $a .$

More commonly, we simply refer to a two-sided limit as a limit. If the left-hand limit does not equal the right-hand limit, or if one of them does not exist, we say the limit does not exist.

The Two-Sided Limit of Function as *x* Approaches *a*

The limit of a function $f (x),$

as $x$

approaches $a,$

is equal to $L,$

that is,

\lim_{x \to a} f (x) = L

if and only if

\lim_{x \to a^{-}} f (x) = \lim_{x \to a^{+}} f (x) .

In other words, the left-hand limit of a function $f (x)$

as $x$

approaches $a$

is equal to the right-hand limit of the same function as $x$

approaches $a .$

If such a limit exists, we refer to the limit as a two-sided limit. Otherwise we say the limit does not exist.

Finding a Limit Using a Graph

To visually determine if a limit exists as $x$

approaches $a,$

we observe the graph of the function when $x$

is very near to $x = a .$

In [link] we observe the behavior of the graph on both sides of $a .$

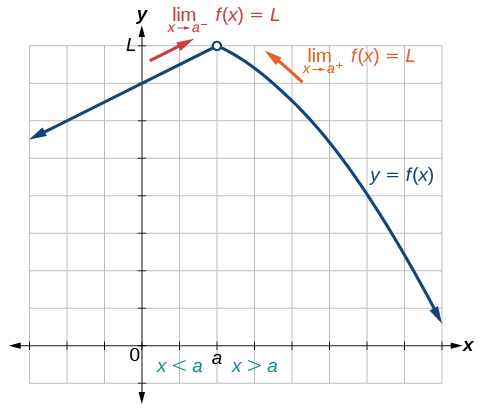
Graph of a function that explains the behavior of a limit at (a, L) where the function is increasing when x is less than a and decreasing when x is greater than a.

To determine if a left-hand limit exists, we observe the branch of the graph to the left of $x = a,$

but near $x = a .$

This is where $x < a .$

We see that the outputs are getting close to some real number $L$

so there is a left-hand limit.

To determine if a right-hand limit exists, observe the branch of the graph to the right of $x = a,$

but near $x = a .$

This is where $x > a .$

We see that the outputs are getting close to some real number $L,$

so there is a right-hand limit.

If the left-hand limit and the right-hand limit are the same, as they are in [link], then we know that the function has a two-sided limit. Normally, when we refer to a “limit,” we mean a two-sided limit, unless we call it a one-sided limit.

Finally, we can look for an output value for the function $f (x)$

when the input value $x$

is equal to $a .$

The coordinate pair of the point would be $(a, f (a)) .$

If such a point exists, then $f (a)$

has a value. If the point does not exist, as in [link], then we say that $f (a)$

does not exist.

Given a function

f( x ),

</math>use a graph to find the limits and a function value as

</math>approaches

</math></strong>

Examine the graph to determine whether a left-hand limit exists.
Examine the graph to determine whether a right-hand limit exists.
If the two one-sided limits exist and are equal, then there is a two-sided limit—what we normally call a “limit.”
If there is a point at $x = a,$
then
$f (a)$
is the corresponding function value.

Finding a Limit Using a Graph

Determine the following limits and function value for the function f
shown in [link].
1. $\lim_{x \to 2^{-}} f (x)$
2. $\lim_{x \to 2^{+}} f (x)$
3. $\lim_{x \to 2} f (x)$
4. $f (2)$
Determine the following limits and function value for the function f
shown in [link].
1. $\lim_{x \to 2^{-}} f (x)$
2. $\lim_{x \to 2^{+}} f (x)$
3. $\lim_{x \to 2} f (x)$
4. $f (2)$

Looking at [link]:
1. $\lim_{x \to 2^{-}} f (x) = 8;$
  when
  $x < 2,$
  but infinitesimally close to 2, the output values get close to
  $y = 8.$
2. $\lim_{x \to 2^{+}} f (x) = 3;$
  when
  $x > 2,$
  but infinitesimally close to 2, the output values approach
  $y = 3.$
3. $\lim_{x \to 2} f (x)$
  does not exist because
  $\lim_{x \to 2^{-}} f (x) \neq \lim_{x \to 2^{+}} f (x);$
  the left and right-hand limits are not equal.
4. $f (2) = 3$
  because the graph of the function
  $f$
  passes through the point
  $(2, f (2))$
  or
  $(2, 3) .$
Looking at [link]:
1. $\lim_{x \to 2^{-}} f (x) = 8;$
  when
  $x < 2$
  but infinitesimally close to 2, the output values approach
  $y = 8.$
2. $\lim_{x \to 2^{+}} f (x) = 8;$
  when
  $x > 2$
  but infinitesimally close to 2, the output values approach
  $y = 8.$
3. $\lim_{x \to 2} f (x) = 8$
  because
  $\lim_{x \to 2^{-}} f (x) = \lim_{x \to 2^{+}} f (x) = 8;$
  the left and right-hand limits are equal.
4. $f (2) = 4$
  because the graph of the function
  $f$
  passes through the point
  $(2, f (2))$
  or
  $(2, 4) .$

Using the graph of the function $y = f (x)$

shown in [link], estimate the following limits.

Graph of a piecewise function that has three segments: 1) negative infinity to 0, 2) 0 to 2, and 3) 2 to positive inifnity, which has a discontinuity at (4, 4)

a. 0; b. 2; c. does not exist; d. $- 2;$

e. 0; f. does not exist; g. 4; h. 4; i. 4

Finding a Limit Using a Table

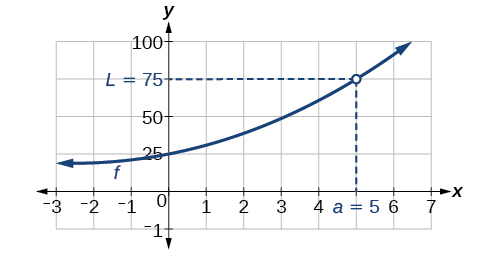
Creating a table is a way to determine limits using numeric information. We create a table of values in which the input values of $x$

approach $a$

from both sides. Then we determine if the output values get closer and closer to some real value, the limit $L .$

Let’s consider an example using the following function:

\lim_{x \to 5} (\frac{x^{3} - 125}{x - 5})

To create the table, we evaluate the function at values close to $x = 5.$

We use some input values less than 5 and some values greater than 5 as in [link]. The table values show that when $x > 5$

but nearing 5, the corresponding output gets close to 75. When $x > 5$

but nearing 5, the corresponding output also gets close to 75.

Table shows that as x values approach 5 from the positive or negative direction, f(x) gets very close to 75. But when x is equal to 5, y is undefined.

Because

\lim_{x \to 5^{-}} f (x) = 75 = \lim_{x \to 5^{+}} f (x),

then

\lim_{x \to 5} f (x) = 75.

Remember that $f (5)$

does not exist.

Given a function $f,$

use a table to find the limit as $x$

approaches $a$

and the value of $f (a),$

if it exists.

Choose several input values that approach $a$
from both the left and right. Record them in a table.
Evaluate the function at each input value. Record them in the table.
Determine if the table values indicate a left-hand limit and a right-hand limit.
If the left-hand and right-hand limits exist and are equal, there is a two-sided limit.
Replace $x$
with
$a$
to find the value of
$f (a) .$

Finding a Limit Using a Table

Numerically estimate the limit of the following expression by setting up a table of values on both sides of the limit.

\lim_{x \to 0} (\frac{5 \sin (x)}{3 x})

We can estimate the value of a limit, if it exists, by evaluating the function at values near $x = 0.$

We cannot find a function value for $x = 0$

directly because the result would have a denominator equal to 0, and thus would be undefined.

f (x) = \frac{5 \sin (x)}{3 x}

We create [link] by choosing several input values close to $x = 0,$

with half of them less than $x = 0$

and half of them greater than $x = 0.$

Note that we need to be sure we are using radian mode. We evaluate the function at each input value to complete the table.

The table values indicate that when $x < 0$

but approaching 0, the corresponding output nears $\frac{5}{3} .$

When $x > 0$

but approaching 0, the corresponding output also nears $\frac{5}{3} .$

Table shows that as x values approach 0 from the positive or negative direction, f(x) gets very close to 5 over 3. But when x is equal to 0, y is undefined.

Because

\lim_{x \to 0^{-}} f (x) = \frac{5}{3} = \lim_{x \to 0^{+}} f (x),

then

\lim_{x \to 0} f (x) = \frac{5}{3} .

Is it possible to check our answer using a graphing utility?

Yes. We previously used a table to find a limit of 75 for the function

f(x)= x 3 −125 x−5

</math>as

</math>approaches 5. To check, we graph the function on a viewing window as shown in [link]. A graphical check shows both branches of the graph of the function get close to the output 75 as

</math>nears 5. Furthermore, we can use the ‘trace’ feature of a graphing calculator. By appraoching

x=5

</math>we may numerically observe the corresponding outputs getting close to

75.

</math></em>

Graph of an increasing function with a discontinuity at (5, 75)

Numerically estimate the limit of the following function by making a table:

\lim_{x \to 0} (\frac{20 \sin (x)}{4 x})

\lim_{x \to 0} (\frac{20 \sin (x)}{4 x}) = 5

Table showing that f(x) approaches 5 from either side as x approaches 0 from either side.

Is one method for determining a limit better than the other?

No. Both methods have advantages. Graphing allows for quick inspection. Tables can be used when graphical utilities aren’t available, and they can be calculated to a higher precision than could be seen with an unaided eye inspecting a graph.

Using a Graphing Utility to Determine a Limit

With the use of a graphing utility, if possible, determine the left- and right-hand limits of the following function as $x$

approaches 0. If the function has a limit as $x$

approaches 0, state it. If not, discuss why there is no limit.

f (x) = 3 \sin (\frac{π}{x})

We can use a graphing utility to investigate the behavior of the graph close to $x = 0.$

Centering around $x = 0,$

we choose two viewing windows such that the second one is zoomed in closer to $x = 0$

than the first one. The result would resemble [link] for $[- 2, 2]$

by $[- 3, 3] .$

Graph of a sinusodial function zoomed in at [-2, 2] by [-3, 3].

The result would resemble [link] for $[−0.1, 0.1]$

by $[−3, 3] .$

Graph of the same sinusodial function as in the previous image zoomed in at [-0.1, 0.1] by [-3. 3].

The closer we get to 0, the greater the swings in the output values are. That is not the behavior of a function with either a left-hand limit or a right-hand limit. And if there is no left-hand limit or right-hand limit, there certainly is no limit to the function $f (x)$

as $x$

approaches 0.

We write

\lim_{x \to 0^{-}} (3 \sin (\frac{π}{x})) does not exist .

\lim_{x \to 0^{+}} (3 \sin (\frac{π}{x})) does not exist .

\lim_{x \to 0} (3 \sin (\frac{π}{x})) does not exist .

Numerically estimate the following limit: $\lim_{x \to 0} (\sin (\frac{2}{x})) .$

does not exist

Access these online resources for additional instruction and practice with finding limits.

Key Concepts

A function has a limit if the output values approach some value $L$
as the input values approach some quantity
$a .$
See [link].
A shorthand notation is used to describe the limit of a function according to the form $\lim_{x \to a} f (x) = L,$
which indicates that as
$x$
approaches
$a,$
both from the left of
$x = a$
and the right of
$x = a,$
the output value gets close to
$L .$
A function has a left-hand limit if $f (x)$
approaches
$L$
as
$x$
approaches
$a$
where
$x < a .$
A function has a right-hand limit if
$f (x)$
approaches
$L$
as
$x$
approaches
$a$
where
$x > a .$
A two-sided limit exists if the left-hand limit and the right-hand limit of a function are the same. A function is said to have a limit if it has a two-sided limit.
A graph provides a visual method of determining the limit of a function.
If the function has a limit as $x$
approaches
$a,$
the branches of the graph will approach the same
$y -$
coordinate near
$x = a$
from the left and the right. See [link].
A table can be used to determine if a function has a limit. The table should show input values that approach $a$
from both directions so that the resulting output values can be evaluated. If the output values approach some number, the function has a limit. See [link].
A graphing utility can also be used to find a limit. See [link].

Section Exercises

Verbal

Explain the difference between a value at $x = a$

and the limit as $x$

approaches $a .$

The value of the function, the output, at $x = a$

is $f (a) .$

When the $\lim_{x \to a} f (x)$

is taken, the values of $x$

get infinitely close to $a$

but never equal $a .$

As the values of $x$

approach $a$

from the left and right, the limit is the value that the function is approaching.

Explain why we say a function does not have a limit as $x$

approaches $a$

if, as $x$

approaches $a,$

the left-hand limit is not equal to the right-hand limit.

Graphical

For the following exercises, estimate the functional values and the limits from the graph of the function $f$

provided in [link].

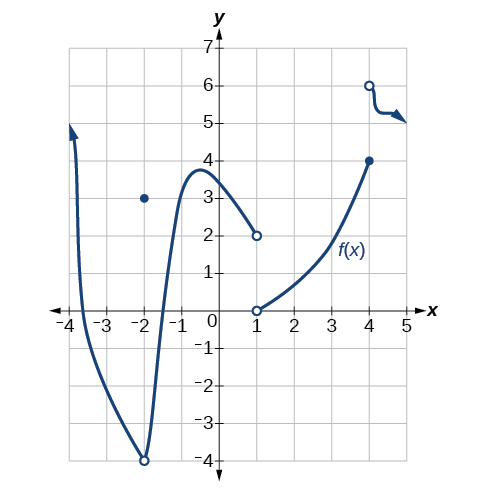
A piecewise function with discontinuities at x = -2, x = 1, and x = 4.

\lim_{x \to - 2^{-}} f (x)

–4

\lim_{x \to - 2^{+}} f (x)

\lim_{x \to - 2} f (x)

–4

f (−2)

\lim_{x \to - 1^{-}} f (x)

\lim_{x \to 1^{+}} f (x)

\lim_{x \to 1} f (x)

does not exist

f (1)

\lim_{x \to 4^{-}} f (x)

\lim_{x \to 4^{+}} f (x)

\lim_{x \to 4} f (x)

does not exist

f (4)

For the following exercises, draw the graph of a function from the functional values and limits provided.

\lim_{x \to 0^{-}} f (x) = 2, \lim_{x \to 0^{+}} f (x) = - 3, \lim_{x \to 2} f (x) = 2, f (0) = 4, f (2) = - 1, f (- 3) does not exist .

Answers will vary.

\lim_{x \to 2^{-}} f (x) = 0, \lim_{x \to 2^{+}} = - 2, \lim_{x \to 0} f (x) = 3, f (2) = 5, f (0)

Answers will vary.

\lim_{x \to 2^{-}} f (x) = 2, \lim_{x \to 2^{+}} f (x) = - 3, \lim_{x \to 0} f (x) = 5, f (0) = 1, f (1) = 0

Answers will vary.

\lim_{x \to 3^{-}} f (x) = 0, \lim_{x \to 3^{+}} f (x) = 5, \lim_{x \to 5} f (x) = 0, f (5) = 4, f (3) does not exist .

Answers will vary.

\lim_{x \to 4} f (x) = 6, \lim_{x \to 6^{+}} f (x) = - 1, \lim_{x \to 0} f (x) = 5, f (4) = 6, f (2) = 6

Answers will vary.

\lim_{x \to - 3} f (x) = 2, \lim_{x \to 1^{+}} f (x) = - 2, \lim_{x \to 3} f (x) = - 4, f (- 3) = 0, f (0) = 0

Answers will vary.

\lim_{x \to π} f (x) = π^{2}, \lim_{x \to - π} f (x) = \frac{π}{2}, \lim_{x \to 1^{-}} f (x) = 0, f (π) = \sqrt{2}, f (0) does not exist .

Answers will vary.

For the following exercises, use a graphing calculator to determine the limit to 5 decimal places as $x$

approaches 0.

f (x) = {(1 + x)}^{\frac{1}{x}}

g (x) = {(1 + x)}^{\frac{2}{x}}

7.38906

h (x) = {(1 + x)}^{\frac{3}{x}}

i (x) = {(1 + x)}^{\frac{4}{x}}

54.59815

j (x) = {(1 + x)}^{\frac{5}{x}}

Based on the pattern you observed in the exercises above, make a conjecture as to the limit of $f (x) = {(1 + x)}^{\frac{6}{x}},$

g (x) = {(1 + x)}^{\frac{7}{x}},

and h (x) = {(1 + x)}^{\frac{n}{x}} .

e^{6} \approx 403.428794,

e^{7} \approx 1096.633158,

e^{n}

For the following exercises, use a graphing utility to find graphical evidence to determine the left- and right-hand limits of the function given as $x$

approaches $a .$

If the function has a limit as $x$

approaches $a,$

state it. If not, discuss why there is no limit.

(x) = {\begin{array}{l} \| x \| - 1, & if x \neq 1 \\ x^{3}, & if x = 1 \end{array} a = 1

(x) = {\begin{array}{l} \frac{1}{x + 1}, & if x = - 2 \\ {(x + 1)}^{2}, & if x \neq - 2 \end{array} a = - 2

\lim_{x \to - 2} f (x) = 1

Numeric

For the following exercises, use numerical evidence to determine whether the limit exists at $x = a .$

If not, describe the behavior of the graph of the function near $x = a .$

Round answers to two decimal places.

f (x) = \frac{x^{2} - 4 x}{16 - x^{2}}; a = 4

f (x) = \frac{x^{2} - x - 6}{x^{2} - 9}; a = 3

\lim_{x \to 3} (\frac{x^{2} - x - 6}{x^{2} - 9}) = \frac{5}{6} \approx 0.83

f (x) = \frac{x^{2} - 6 x - 7}{x^{2} - 7 x}; a = 7

f (x) = \frac{x^{2} - 1}{x^{2} - 3 x + 2}; a = 1

\lim_{x \to 1} (\frac{x^{2} - 1}{x^{2} - 3 x + 2}) = - 2.00

f (x) = \frac{1 - x^{2}}{x^{2} - 3 x + 2}; a = 1

f (x) = \frac{10 - 10 x^{2}}{x^{2} - 3 x + 2}; a = 1

\lim_{x \to 1} (\frac{10 - 10 x^{2}}{x^{2} - 3 x + 2}) = 20.00

f (x) = \frac{x}{6 x^{2} - 5 x - 6}; a = \frac{3}{2}

f (x) = \frac{x}{4 x^{2} + 4 x + 1}; a = - \frac{1}{2}

\lim_{x \to \frac{- 1}{2}} (\frac{x}{4 x^{2} + 4 x + 1})

does not exist. Function values decrease without bound as $x$

approaches –0.5 from either left or right.

f (x) = \frac{2}{x - 4}; a = 4

For the following exercises, use a calculator to estimate the limit by preparing a table of values. If there is no limit, describe the behavior of the function as $x$

approaches the given value.

\lim_{x \to 0} \frac{7 \tan x}{3 x}

\lim_{x \to 0} \frac{7 \tan x}{3 x} = \frac{7}{3}

Table shows as the function approaches 0, the value is 7 over 3 but the function is undefined at 0.

\lim_{x \to 4} \frac{x^{2}}{x - 4}

![Table shows as the function approaches 4, the value does not exist since approaching the limit value from the left is negative infinity and approaching the limit value from the right is positive infinity.](/precalculus-book/resources/CNX_Precalc_Figure_12_01_203.jpg)

\lim_{x \to 0} \frac{2 \sin x}{4 \tan x}

\lim_{x \to 0} \frac{2 \sin x}{4 \tan x} = \frac{1}{2}

Table shows as the function approaches 0, the value is 1 over 2, but the function is undefined at 0.

For the following exercises, use a graphing utility to find numerical or graphical evidence to determine the left and right-hand limits of the function given as $x$

approaches $a .$

If the function has a limit as $x$

approaches $a,$

state it. If not, discuss why there is no limit.

\lim_{x \to 0} e^{e^{\frac{1}{x}}}

\lim_{x \to 0} e^{e^{- \frac{1}{x^{2}}}}

\lim_{x \to 0} e^{e^{- \frac{1}{x^{2}}}} = 1.0

\lim_{x \to 0} \frac{\| x \|}{x}

\lim_{x \to - 1} \frac{\| x + 1 \|}{x + 1}

\lim_{x \to - 1^{-}} \frac{\| x + 1 \|}{x + 1} = \frac{- (x + 1)}{(x + 1)} = - 1

and $\lim_{x \to - 1^{+}} \frac{\| x + 1 \|}{x + 1} = \frac{(x + 1)}{(x + 1)} = 1;$

since the right-hand limit does not equal the left-hand limit, $\lim_{x \to - 1} \frac{\| x + 1 \|}{x + 1}$

does not exist.

\lim_{x \to 5} \frac{\| x - 5 \|}{5 - x}

\lim_{x \to - 1} \frac{1}{{(x + 1)}^{2}}

\lim_{x \to - 1} \frac{1}{{(x + 1)}^{2}}

does not exist. The function increases without bound as $x$

approaches $- 1$

from either side.

\lim_{x \to 1} \frac{1}{{(x - 1)}^{3}}

\lim_{x \to 0} \frac{5}{1 - e^{\frac{2}{x}}}

\lim_{x \to 0} \frac{5}{1 - e^{\frac{2}{x}}}

does not exist. Function values approach 5 from the left and approach 0 from the right.

Use numerical and graphical evidence to compare and contrast the limits of two functions whose formulas appear similar: $f (x) = \| \frac{1 - x}{x} \|$

and $g (x) = \| \frac{1 + x}{x} \|$

as $x$

approaches 0. Use a graphing utility, if possible, to determine the left- and right-hand limits of the functions $f (x)$

and $g (x)$

as $x$

approaches 0. If the functions have a limit as $x$

approaches 0, state it. If not, discuss why there is no limit.

Extensions

According to the Theory of Relativity, the mass $m$

of a particle depends on its velocity $v$

. That is

m = \frac{m_{o}}{\sqrt{1 - (v^{2} / c^{2})}}

where $m_{o}$

is the mass when the particle is at rest and $c$

is the speed of light. Find the limit of the mass, $m,$

as $v$

approaches $c^{-} .$

Through examination of the postulates and an understanding of relativistic physics, as $v \to c,$

m \to \infty .

Take this one step further to the solution,

\lim_{v \to c^{-}} m = \lim_{v \to c^{-}} \frac{m_{o}}{\sqrt{1 - (v^{2} / c^{2})}} = \infty

Allow the speed of light, $c,$

to be equal to 1.0. If the mass, $m,$

is 1, what occurs to $m$

as $v \to c ?$

Using the values listed in [link], make a conjecture as to what the mass is as $v$

approaches 1.00.


$v$	$m$
0.5	1.15
0.9	2.29
0.95	3.20
0.99	7.09
0.999	22.36
0.99999	223.61

Footnotes

1 https://en.wikipedia.org/wiki/Human\_height and http://en.wikipedia.org/wiki/List\_of\_tallest\_people

Glossary

left-hand limit

the limit of values of

f (x)

x

approaches from

a

the left, denoted

\lim_{x \to a^{-}} f (x) = L .

The values of

f (x)

can get as close to the limit

L

as we like by taking values of

x

sufficiently close to

a

such that

x < a

and

x \neq a .

Both

a

and

L

are real numbers.

limit

when it exists, the value,

L,

that the output of a function

f (x)

approaches as the input

x

gets closer and closer to

a

but does not equal

a .

The value of the output,

f (x),

can get as close to

L

as we choose to make it by using input values of

x

sufficiently near to

x = a,

but not necessarily at

x = a .

Both

a

and

L

are real numbers, and

L

is denoted

\lim_{x \to a} f (x) = L .

right-hand limit

the limit of values of

f (x)

x

approaches

a

from the right, denoted

\lim_{x \to a^{+}} f (x) = L .

The values of

f (x)

can get as close to the limit

L

as we like by taking values of

x

sufficiently close to

a

where

x > a,

and

x \neq a .

Both

a

and

L

are real numbers.

two-sided limit

the limit of a function

f (x),

x

approaches

a,

is equal to

L,

that is,

\lim_{x \to a} f (x) = L

if and only if

\lim_{x \to a^{-}} f (x) = \lim_{x \to a^{+}} f (x) .

This work is licensed under a Creative Commons Attribution 4.0 International License.

You can also download for free at http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@8.1

Attribution:

For questions regarding this license, please contact partners@openstaxcollege.org.
If you use this textbook as a bibliographic reference, then you should cite it as follows: OpenStax College, Precalculus. OpenStax CNX. http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@8.1.
If you redistribute this textbook in a print format, then you must include on every physical page the following attribution: "Download for free at http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@8.1."
If you redistribute part of this textbook, then you must retain in every digital format page view (including but not limited to EPUB, PDF, and HTML) and on every physical printed page the following attribution: "Download for free at http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@8.1."