In this section, you will:

Most of us are familiar with orbital motion, such as the motion of a planet around the sun or an electron around an atomic nucleus. Within the planetary system, orbits of planets, asteroids, and comets around a larger celestial body are often elliptical. Comets, however, may take on a parabolic or hyperbolic orbit instead. And, in reality, the characteristics of the planets’ orbits may vary over time. Each orbit is tied to the location of the celestial body being orbited and the distance and direction of the planet or other object from that body. As a result, we tend to use polar coordinates to represent these orbits.
In an elliptical orbit, the periapsis is the point at which the two objects are closest, and the apoapsis is the point at which they are farthest apart. Generally, the velocity of the orbiting body tends to increase as it approaches the periapsis and decrease as it approaches the apoapsis. Some objects reach an escape velocity, which results in an infinite orbit. These bodies exhibit either a parabolic or a hyperbolic orbit about a body; the orbiting body breaks free of the celestial body’s gravitational pull and fires off into space. Each of these orbits can be modeled by a conic section in the polar coordinate system.
Any conic may be determined by three characteristics: a single focus, a fixed line called the directrix, and the ratio of the distances of each to a point on the graph. Consider the parabola
shown in [link].
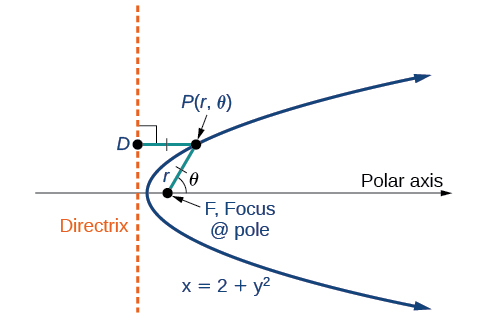
In The Parabola, we learned how a parabola is defined by the focus (a fixed point) and the directrix (a fixed line). In this section, we will learn how to define any conic in the polar coordinate system in terms of a fixed point, the focus
at the pole, and a line, the directrix, which is perpendicular to the polar axis.
If
is a fixed point, the focus, and
is a fixed line, the directrix, then we can let
be a fixed positive number, called the eccentricity, which we can define as the ratio of the distances from a point on the graph to the focus and the point on the graph to the directrix. Then the set of all points
such that
is a conic. In other words, we can define a conic as the set of all points
with the property that the ratio of the distance from
to
to the distance from
to
is equal to the constant
For a conic with eccentricity
the conic is an ellipse
the conic is a parabola
the conic is an hyperbola
With this definition, we may now define a conic in terms of the directrix,
the eccentricity
and the angle
Thus, each conic may be written as a polar equation, an equation written in terms of
and
For a conic with a focus at the origin, if the directrix is
where
is a positive real number, and the eccentricity is a positive real number
the conic has a polar equation
For a conic with a focus at the origin, if the directrix is
where
is a positive real number, and the eccentricity is a positive real number
the conic has a polar equation
Given the polar equation for a conic, identify the type of conic, the directrix, and the eccentricity.
as the coefficient of the trigonometric function in the denominator.
with 1 to determine the shape of the conic.
if cosine is in the denominator and
if sine is in the denominator. Set
equal to the numerator in standard form to solve for
or
For each of the following equations, identify the conic with focus at the origin, the directrix, and the eccentricity.
For each of the three conics, we will rewrite the equation in standard form. Standard form has a 1 as the constant in the denominator. Therefore, in all three parts, the first step will be to multiply the numerator and denominator by the reciprocal of the constant of the original equation,
where
is that constant.
Because
is in the denominator, the directrix is
Comparing to standard form, note that
Therefore, from the numerator,
Since
the conic is an ellipse. The eccentricity is
and the directrix is
Because
is in the denominator, the directrix is
Comparing to standard form,
Therefore, from the numerator,
Since
the conic is a hyperbola. The eccentricity is
and the directrix is
Because sine is in the denominator, the directrix is
Comparing to standard form,
Therefore, from the numerator,
Because
the conic is a parabola. The eccentricity is
and the directrix is
Identify the conic with focus at the origin, the directrix, and the eccentricity for
ellipse;
When graphing in Cartesian coordinates, each conic section has a unique equation. This is not the case when graphing in polar coordinates. We must use the eccentricity of a conic section to determine which type of curve to graph, and then determine its specific characteristics. The first step is to rewrite the conic in standard form as we have done in the previous example. In other words, we need to rewrite the equation so that the denominator begins with 1. This enables us to determine
and, therefore, the shape of the curve. The next step is to substitute values for
and solve for
to plot a few key points. Setting
equal to
and
provides the vertices so we can create a rough sketch of the graph.
Graph
First, we rewrite the conic in standard form by multiplying the numerator and denominator by the reciprocal of 3, which is
Because
we will graph a parabola with a focus at the origin. The function has a
and there is an addition sign in the denominator, so the directrix is
The directrix is
Plotting a few key points as in [link] will enable us to see the vertices. See [link].
| A | B | C | D | |
|---|---|---|---|---|
| undefined |
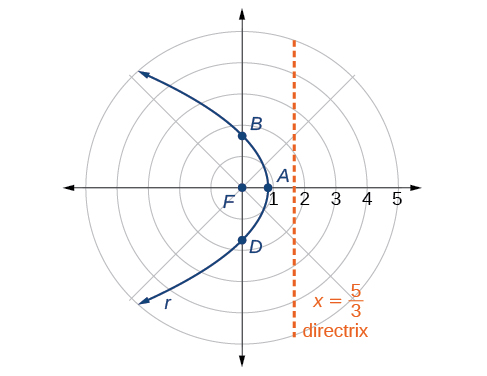
Graph
First, we rewrite the conic in standard form by multiplying the numerator and denominator by the reciprocal of 2, which is
Because
so we will graph a hyperbola with a focus at the origin. The function has a
term and there is a subtraction sign in the denominator, so the directrix is
The directrix is
Plotting a few key points as in [link] will enable us to see the vertices. See [link].
| A | B | C | D | |
|---|---|---|---|---|

Graph
First, we rewrite the conic in standard form by multiplying the numerator and denominator by the reciprocal of 5, which is
Because
so we will graph an ellipse with a focus at the origin. The function has a
and there is a subtraction sign in the denominator, so the directrix is
The directrix is
Plotting a few key points as in [link] will enable us to see the vertices. See [link].
| A | B | C | D | |
|---|---|---|---|---|

Graph
So far we have been using polar equations of conics to describe and graph the curve. Now we will work in reverse; we will use information about the origin, eccentricity, and directrix to determine the polar equation.
Given the focus, eccentricity, and directrix of a conic, determine the polar equation.
we use the general polar form in terms of sine. If the directrix is given in terms of
we use the general polar form in terms of cosine.
use subtraction. If
use addition.
in the numerator, and simplify the equation.
Find the polar form of the conic given a focus at the origin,
and directrix
The directrix is
so we know the trigonometric function in the denominator is sine.
Because
so we know there is a subtraction sign in the denominator. We use the standard form of
and
and
Therefore,
Find the polar form of a conic given a focus at the origin,
and directrix
Because the directrix is
we know the function in the denominator is cosine. Because
so we know there is an addition sign in the denominator. We use the standard form of
and
and
Therefore,
Find the polar form of the conic given a focus at the origin,
and directrix
Convert the conic
to rectangular form.
We will rearrange the formula to use the identities
Convert the conic
to rectangular form.
Access these online resources for additional instruction and practice with conics in polar coordinates.
Visit this website for additional practice questions from Learningpod.
at the pole, and a line, the directrix, which is perpendicular to the polar axis.
where eccentricity
is a positive real number. Each conic may be written in terms of its polar equation. See [link].
and
to convert the equation for a conic from polar to rectangular form. See [link].
Explain how eccentricity determines which conic section is given.
If eccentricity is less than 1, it is an ellipse. If eccentricity is equal to 1, it is a parabola. If eccentricity is greater than 1, it is a hyperbola.
If a conic section is written as a polar equation, what must be true of the denominator?
If a conic section is written as a polar equation, and the denominator involves
what conclusion can be drawn about the directrix?
The directrix will be parallel to the polar axis.
If the directrix of a conic section is perpendicular to the polar axis, what do we know about the equation of the graph?
What do we know about the focus/foci of a conic section if it is written as a polar equation?
One of the foci will be located at the origin.
For the following exercises, identify the conic with a focus at the origin, and then give the directrix and eccentricity.
Parabola with
and directrix
units below the pole.
Hyperbola with
and directrix
units above the pole.
Parabola with
and directrix
units to the right of the pole.
Ellipse with
and directrix
units to the right of the pole.
Hyperbola with
and directrix
units above the pole.
Hyperbola with
and directrix
units to the right of the pole.
For the following exercises, convert the polar equation of a conic section to a rectangular equation.
For the following exercises, graph the given conic section. If it is a parabola, label the vertex, focus, and directrix. If it is an ellipse, label the vertices and foci. If it is a hyperbola, label the vertices and foci.
For the following exercises, find the polar equation of the conic with focus at the origin and the given eccentricity and directrix.
Directrix:
Directrix:
Directrix:
Directrix:
Directrix:
Directrix:
Directrix:
Directrix:
Directrix:
Directrix:
Directrix:
Directrix:
Directrix:
Recall from Rotation of Axes that equations of conics with an
term have rotated graphs. For the following exercises, express each equation in polar form with
as a function of
For the following exercises, write the equation of the ellipse in standard form. Then identify the center, vertices, and foci.
center:
vertices:
foci:
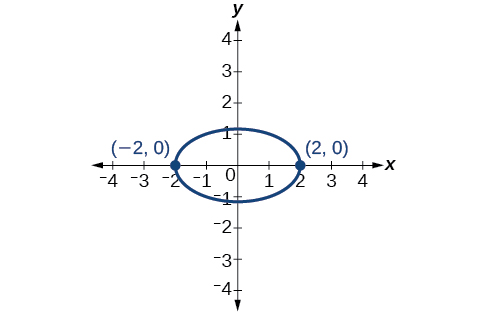
For the following exercises, graph the ellipse, noting center, vertices, and foci.
center:
vertices:
foci:
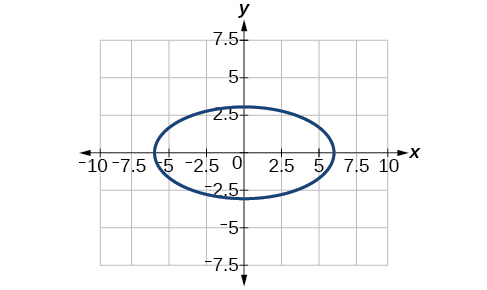
center:
vertices:
foci:
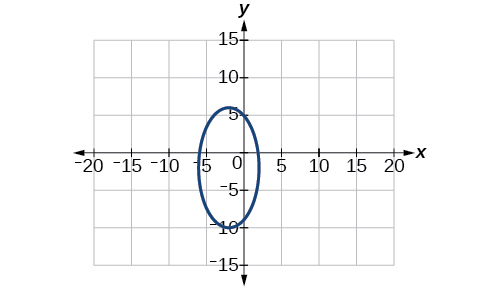
For the following exercises, use the given information to find the equation for the ellipse.
Center at
focus at
vertex at
Center at
vertex at
focus at
A whispering gallery is to be constructed such that the foci are located 35 feet from the center. If the length of the gallery is to be 100 feet, what should the height of the ceiling be?
Approximately 35.71 feet
For the following exercises, write the equation of the hyperbola in standard form. Then give the center, vertices, and foci.
center:
vertices:
foci:
center:
vertices:
foci:
For the following exercises, graph the hyperbola, labeling vertices and foci.
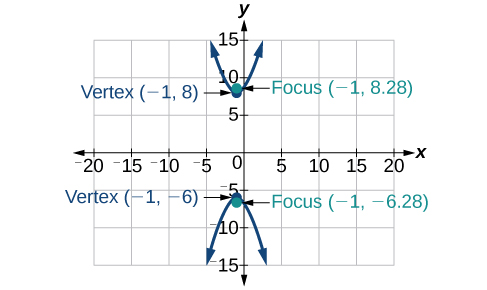
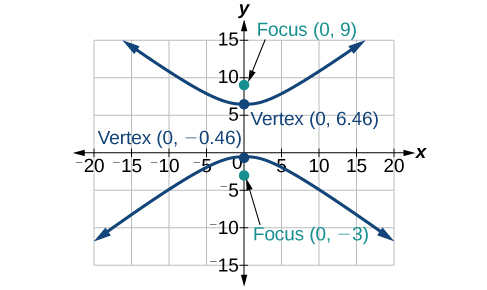
For the following exercises, find the equation of the hyperbola.
Center at
vertex at
focus at
Foci at
and
vertex at
For the following exercises, write the equation of the parabola in standard form. Then give the vertex, focus, and directrix.
vertex:
focus:
directrix:
vertex:
focus:
directrix:
For the following exercises, graph the parabola, labeling vertex, focus, and directrix.
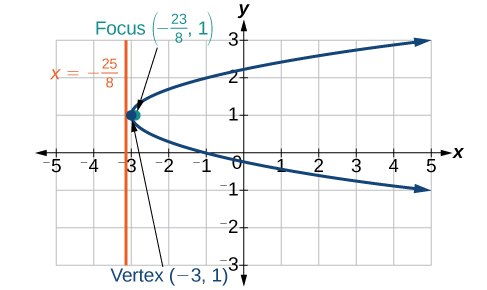
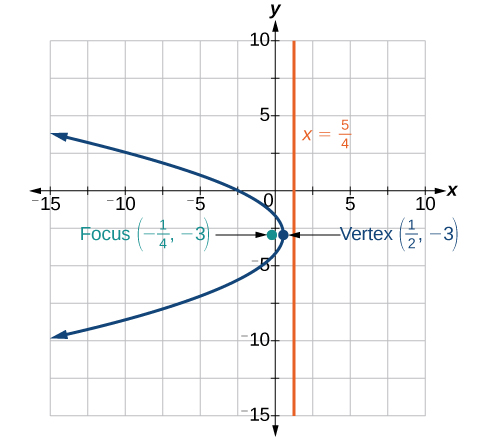
For the following exercises, write the equation of the parabola using the given information.
Focus at
directrix is
Focus at
directrix is
A cable TV receiving dish is the shape of a paraboloid of revolution. Find the location of the receiver, which is placed at the focus, if the dish is 5 feet across at its opening and 1.5 feet deep.
For the following exercises, determine which of the conic sections is represented.
parabola
ellipse
For the following exercises, determine the angle
that will eliminate the
term, and write the corresponding equation without the
term.
For the following exercises, graph the equation relative to the
system in which the equation has no
term.
For the following exercises, given the polar equation of the conic with focus at the origin, identify the eccentricity and directrix.
Hyperbola with
and directrix
units to the left of the pole.
Ellipse with
and directrix
unit above the pole.
For the following exercises, graph the conic given in polar form. If it is a parabola, label the vertex, focus, and directrix. If it is an ellipse or a hyperbola, label the vertices and foci.
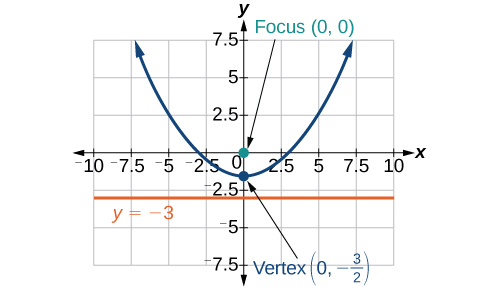

For the following exercises, given information about the graph of a conic with focus at the origin, find the equation in polar form.
Directrix is
and eccentricity
Directrix is
and eccentricity
For the following exercises, write the equation in standard form and state the center, vertices, and foci.
center:
vertices:
foci:
For the following exercises, sketch the graph, identifying the center, vertices, and foci.
center:
vertices:
foci:
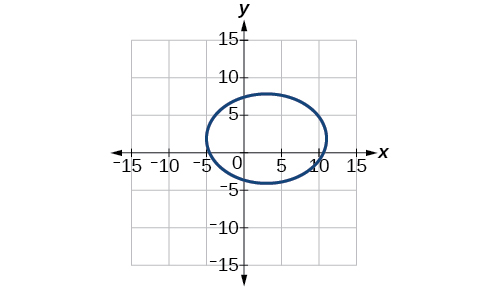
Write the standard form equation of an ellipse with a center at
vertex at
and focus at
A whispering gallery is to be constructed with a length of 150 feet. If the foci are to be located 20 feet away from the wall, how high should the ceiling be?
For the following exercises, write the equation of the hyperbola in standard form, and give the center, vertices, foci, and asymptotes.
center:
vertices
foci:
asymptotes:
For the following exercises, graph the hyperbola, noting its center, vertices, and foci. State the equations of the asymptotes.
center:
vertices:
foci:
asymptotes:
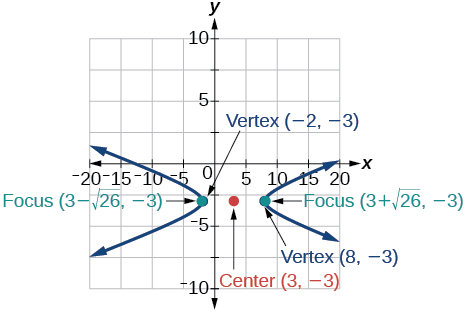
Write the standard form equation of a hyperbola with foci at
and
and a vertex at
For the following exercises, write the equation of the parabola in standard form, and give the vertex, focus, and equation of the directrix.
vertex:
focus:
directrix:
For the following exercises, graph the parabola, labeling the vertex, focus, and directrix.
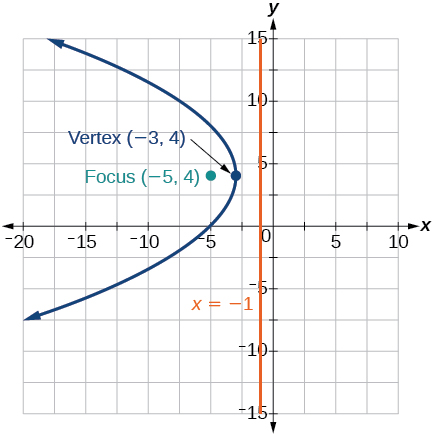
Write the equation of a parabola with a focus at
and directrix
A searchlight is shaped like a paraboloid of revolution. If the light source is located 1.5 feet from the base along the axis of symmetry, and the depth of the searchlight is 3 feet, what should the width of the opening be?
Approximately
feet
For the following exercises, determine which conic section is represented by the given equation, and then determine the angle
that will eliminate the
term.
parabola;
For the following exercises, rewrite in the
system without the
term, and graph the rotated graph.
For the following exercises, identify the conic with focus at the origin, and then give the directrix and eccentricity.
Hyperbola with
and directrix
units to the right of the pole.
For the following exercises, graph the given conic section. If it is a parabola, label vertex, focus, and directrix. If it is an ellipse or a hyperbola, label vertices and foci.
Find a polar equation of the conic with focus at the origin, eccentricity of
and directrix:
on the graph to the focus
and to the directrix
represented by
where
is a positive real number
and

You can also download for free at http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@8.1
Attribution: