In this section, you will:
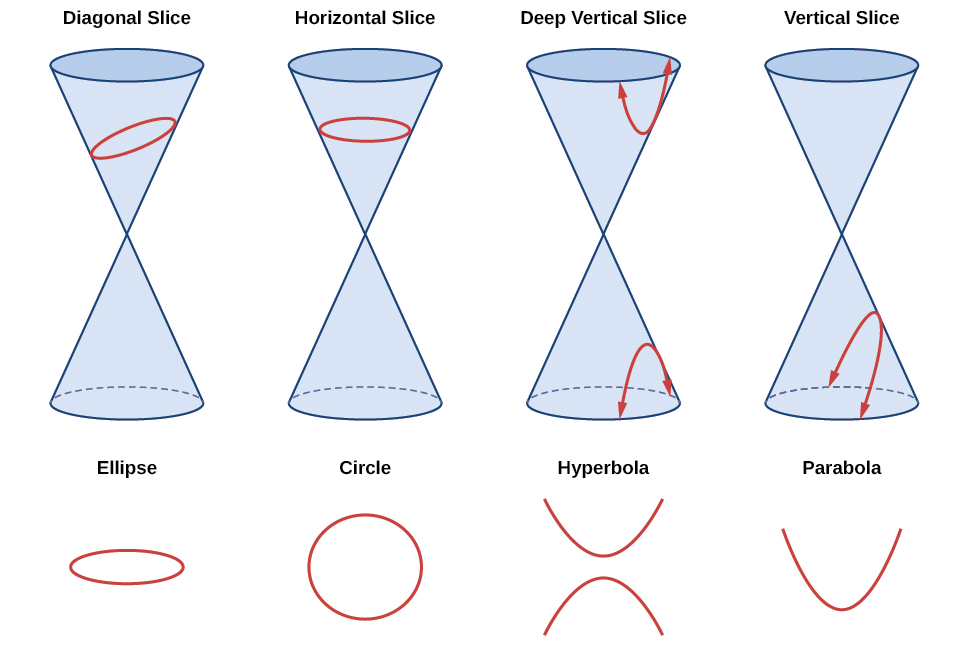
As we have seen, conic sections are formed when a plane intersects two right circular cones aligned tip to tip and extending infinitely far in opposite directions, which we also call a cone. The way in which we slice the cone will determine the type of conic section formed at the intersection. A circle is formed by slicing a cone with a plane perpendicular to the axis of symmetry of the cone. An ellipse is formed by slicing a single cone with a slanted plane not perpendicular to the axis of symmetry. A parabola is formed by slicing the plane through the top or bottom of the double-cone, whereas a hyperbola is formed when the plane slices both the top and bottom of the cone. See [link].

Ellipses, circles, hyperbolas, and parabolas are sometimes called the nondegenerate conic sections, in contrast to the degenerate conic sections, which are shown in [link]. A degenerate conic results when a plane intersects the double cone and passes through the apex. Depending on the angle of the plane, three types of degenerate conic sections are possible: a point, a line, or two intersecting lines.

In previous sections of this chapter, we have focused on the standard form equations for nondegenerate conic sections. In this section, we will shift our focus to the general form equation, which can be used for any conic. The general form is set equal to zero, and the terms and coefficients are given in a particular order, as shown below.
where
and
are not all zero. We can use the values of the coefficients to identify which type conic is represented by a given equation.
You may notice that the general form equation has an
term that we have not seen in any of the standard form equations. As we will discuss later, the
term rotates the conic whenever
is not equal to zero.
| Conic Sections | Example |
|---|---|
| ellipse |
| circle |
| hyperbola |
| parabola |
| one line |
| intersecting lines |
| parallel lines |
| a point |
| no graph |
A conic section has the general form
where
and
are not all zero.
[link] summarizes the different conic sections where
and
and
are nonzero real numbers. This indicates that the conic has not been rotated.
| ellipse | |
| circle | |
| hyperbola | whereandare positive |
| parabola |
Given the equation of a conic, identify the type of conic.
and
from the general form.
and
are nonzero, have the same sign, and are not equal to each other, then the graph may be an ellipse.
and
are equal and nonzero and have the same sign, then the graph may be a circle.
and
are nonzero and have opposite signs, then the graph may be a hyperbola.
or
is zero, then the graph may be a parabola.
If B = 0, the conic section will have a vertical and/or horizontal axes. If B does not equal 0, as shown below, the conic section is rotated. Notice the phrase “may be” in the definitions. That is because the equation may not represent a conic section at all, depending on the values of A, B, C, D, E, and F. For example, the degenerate case of a circle or an ellipse is a point: * * *
when A and B have the same sign. * * *
The degenerate case of a hyperbola is two intersecting straight lines:
when A and B have opposite signs. * * *
On the other hand, the equation,
when A and B are positive does not represent a graph at all, since there are no real ordered pairs which satisfy it.
Identify the graph of each of the following nondegenerate conic sections.
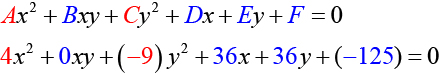
and
so we observe that
and
have opposite signs. The graph of this equation is a hyperbola.
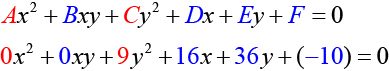
and
We can determine that the equation is a parabola, since
is zero.
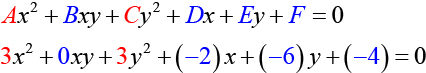
and
Because
the graph of this equation is a circle.
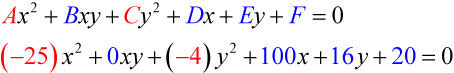
and
Because
and
the graph of this equation is an ellipse.
Identify the graph of each of the following nondegenerate conic sections.
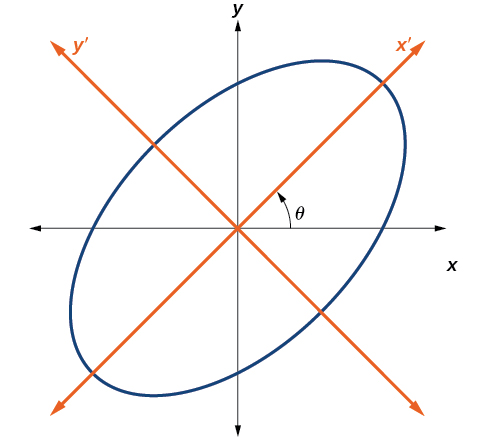
Until now, we have looked at equations of conic sections without an
term, which aligns the graphs with the x- and y-axes. When we add an
term, we are rotating the conic about the origin. If the x- and y-axes are rotated through an angle, say
then every point on the plane may be thought of as having two representations:
on the Cartesian plane with the original x-axis and y-axis, and
on the new plane defined by the new, rotated axes, called the x'-axis and y'-axis. See [link].
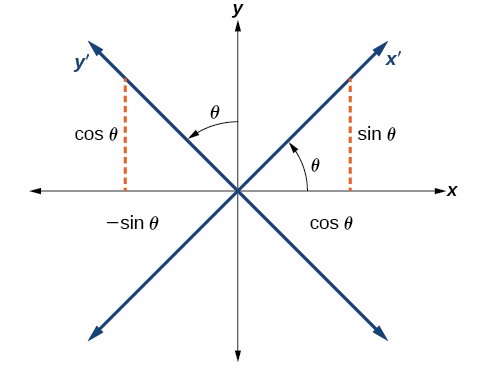
We will find the relationships between
and
on the Cartesian plane with
and
on the new rotated plane. See [link].
The original coordinate x- and y-axes have unit vectors
and
The rotated coordinate axes have unit vectors
and
The angle
is known as the angle of rotation. See [link]. We may write the new unit vectors in terms of the original ones.
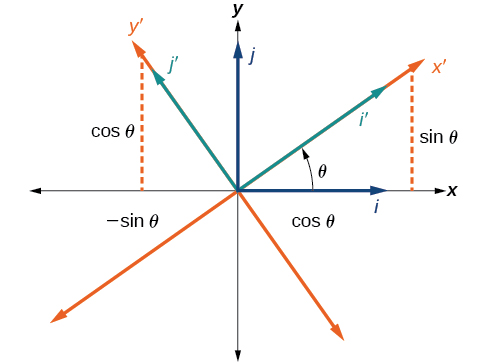
Consider a vector
</math></strong>in the new coordinate plane. It may be represented in terms of its coordinate axes.
Because
we have representations of
and
in terms of the new coordinate system.
If a point
on the Cartesian plane is represented on a new coordinate plane where the axes of rotation are formed by rotating an angle
from the positive x-axis, then the coordinates of the point with respect to the new axes are
We can use the following equations of rotation to define the relationship between
and
and
Given the equation of a conic, find a new representation after rotating through an angle.
and
where
and
and
into in the given equation, then simplify.
and
in standard form.
Find a new representation of the equation
after rotating through an angle of
Find
and
where
and
Because
and
Substitute
and
into
Simplify.
Write the equations with
and
in the standard form.
This equation is an ellipse. [link] shows the graph.
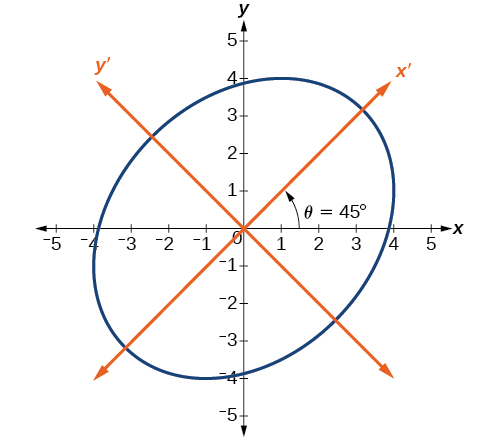
Now that we can find the standard form of a conic when we are given an angle of rotation, we will learn how to transform the equation of a conic given in the form
into standard form by rotating the axes. To do so, we will rewrite the general form as an equation in the
and
coordinate system without the
term, by rotating the axes by a measure of
that satisfies
We have learned already that any conic may be represented by the second degree equation
where
and
are not all zero. However, if
then we have an
term that prevents us from rewriting the equation in standard form. To eliminate it, we can rotate the axes by an acute angle
where
then
is in the first quadrant, and
is between
then
is in the second quadrant, and
is between
then
**Given an equation for a conic in the
system, rewrite the equation without the
term in terms of
and
where the
and
axes are rotations of the standard axes by
degrees.**
and
and
into
and
and
into in the given equation, and then simplify.
and
in the standard form with respect to the rotated axes.
Rewrite the equation
in the
system without an
term.
First, we find
See [link].
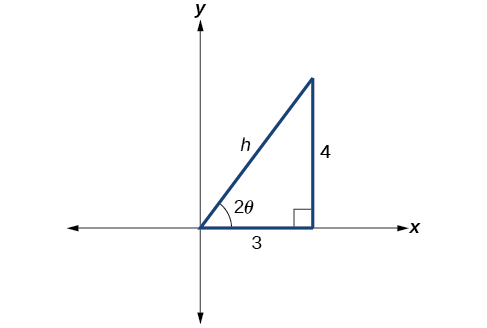
So the hypotenuse is
Next, we find
and
Substitute the values of
and
into
and
and
Substitute the expressions for
and
into in the given equation, and then simplify.
Write the equations with
and
in the standard form with respect to the new coordinate system.
[link] shows the graph of the ellipse.
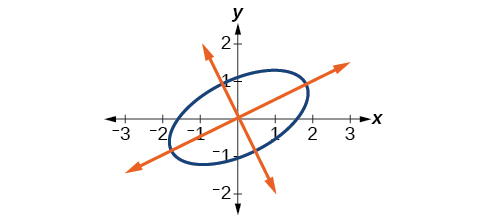
Rewrite the
in the
system without the
term.
Graph the following equation relative to the
system:
Now we have come full circle. How do we identify the type of conic described by an equation? What happens when the axes are rotated? Recall, the general form of a conic is
If we apply the rotation formulas to this equation we get the form
It may be shown that
The expression does not vary after rotation, so we call the expression invariant. The discriminant,
is invariant and remains unchanged after rotation. Because the discriminant remains unchanged, observing the discriminant enables us to identify the conic section.
If the equation
is transformed by rotating axes into the equation
then
The equation
is an ellipse, a parabola, or a hyperbola, or a degenerate case of one of these.
If the discriminant,
is
the conic section is an ellipse
the conic section is a parabola
the conic section is a hyperbola
Identify the conic for each of the following without rotating axes.
and
Now, we find the discriminant.
Therefore,
represents an ellipse.
and
Now, we find the discriminant.
Therefore,
represents an ellipse.
Identify the conic for each of the following without rotating axes.
Access this online resource for additional instruction and practice with conic sections and rotation of axes.
| General Form equation of a conic section |
| Rotation of a conic section |
| Angle of rotation |
where
and
are not all zero. The values of
and
determine the type of conic. See [link].
term have been rotated about the origin. See [link].
and
coordinate system without the
What effect does the
term have on the graph of a conic section?
The
term causes a rotation of the graph to occur.
If the equation of a conic section is written in the form
and
what can we conclude?
If the equation of a conic section is written in the form
and
what can we conclude?
The conic section is a hyperbola.
Given the equation
what can we conclude if
For the equation
the value of
that satisfies
gives us what information?
It gives the angle of rotation of the axes in order to eliminate the
term.
For the following exercises, determine which conic section is represented based on the given equation.
parabola
hyperbola
ellipse
parabola
parabola
ellipse
For the following exercises, find a new representation of the given equation after rotating through the given angle.
For the following exercises, determine the angle
that will eliminate the
term and write the corresponding equation without the
term.
For the following exercises, rotate through the given angle based on the given equation. Give the new equation and graph the original and rotated equation.
For the following exercises, graph the equation relative to the
system in which the equation has no
term.
For the following exercises, determine the angle of rotation in order to eliminate the
term. Then graph the new set of axes.
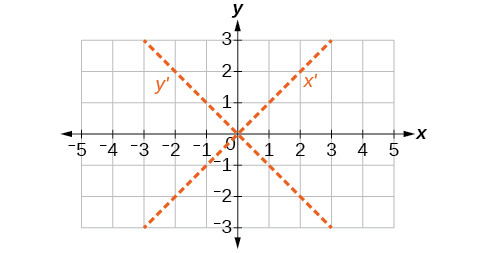
For the following exercises, determine the value of
based on the given equation.
Given
find
for the graph to be a parabola.
Given
find
for the graph to be an ellipse.
Given
find
for the graph to be a hyperbola.
Given
find
for the graph to be a parabola.
Given
find
for the graph to be an ellipse.
then
is between
if
then
is between
and if
then

You can also download for free at http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@8.1
Attribution: