
In this section you will:
It is the bottom of the ninth inning, with two outs and two men on base. The home team is losing by two runs. The batter swings and hits the baseball at 140 feet per second and at an angle of approximately
to the horizontal. How far will the ball travel? Will it clear the fence for a game-winning home run? The outcome may depend partly on other factors (for example, the wind), but mathematicians can model the path of a projectile and predict approximately how far it will travel using parametric equations. In this section, we’ll discuss parametric equations and some common applications, such as projectile motion problems.

In lieu of a graphing calculator or a computer graphing program, plotting points to represent the graph of an equation is the standard method. As long as we are careful in calculating the values, point-plotting is highly dependable.
Given a pair of parametric equations, sketch a graph by plotting points.
and
for values of
over the interval for which the functions are defined.
Sketch the graph of the parametric equations
Construct a table of values for
and
as in [link], and plot the points in a plane.
The graph is a parabola with vertex at the point
opening to the right. See [link].
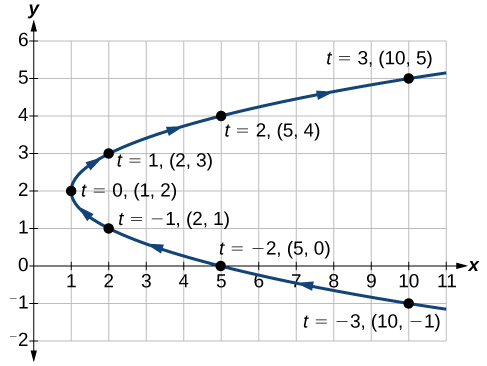
As values for
progress in a positive direction from 0 to 5, the plotted points trace out the top half of the parabola. As values of
become negative, they trace out the lower half of the parabola. There are no restrictions on the domain. The arrows indicate direction according to increasing values of
The graph does not represent a function, as it will fail the vertical line test. The graph is drawn in two parts: the positive values for
and the negative values for
Sketch the graph of the parametric equations
Construct a table of values for the given parametric equations and sketch the graph:
Construct a table like that in [link] using angle measure in radians as inputs for
and evaluating
and
Using angles with known sine and cosine values for
makes calculations easier.
| 0 |
[link] shows the graph.
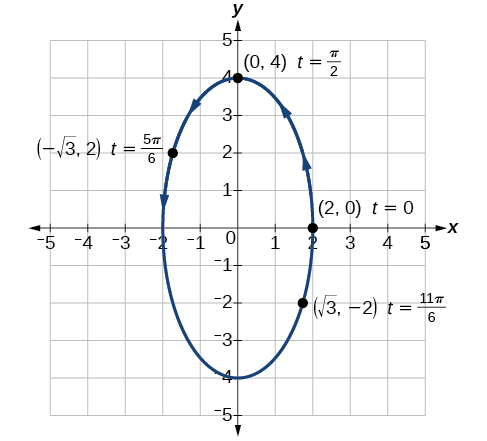
By the symmetry shown in the values of
and
we see that the parametric equations represent an ellipse. The ellipse is mapped in a counterclockwise direction as shown by the arrows indicating increasing
values.
We have seen that parametric equations can be graphed by plotting points. However, a graphing calculator will save some time and reveal nuances in a graph that may be too tedious to discover using only hand calculations.
Make sure to change the mode on the calculator to parametric (PAR). To confirm, the
window should show
instead of
Graph the parametric equations:
Graph the parametric equations
and
First, construct the graph using data points generated from the parametric form. Then graph the rectangular form of the equation. Compare the two graphs.
Construct a table of values like that in [link].
Plot the
values from the table. See [link].
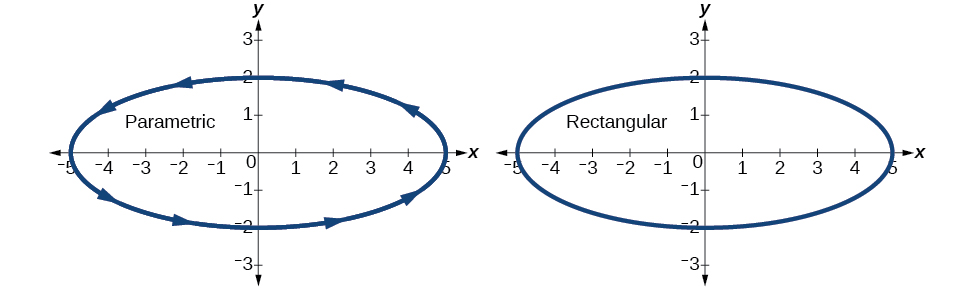
Next, translate the parametric equations to rectangular form. To do this, we solve for
in either
or
and then substitute the expression for
in the other equation. The result will be a function
if solving for
as a function of
or
if solving for
as a function of
Then, use the Pythagorean Theorem.
In [link], the data from the parametric equations and the rectangular equation are plotted together. The parametric equations are plotted in blue; the graph for the rectangular equation is drawn on top of the parametric in a dashed style colored red. Clearly, both forms produce the same graph.
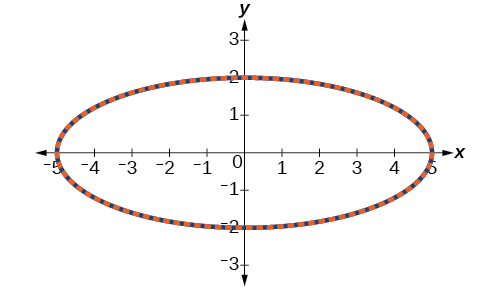
Graph the parametric equations
and
and the rectangular equivalent
on the same coordinate system.
Construct a table of values for the parametric equations, as we did in the previous example, and graph
on the same grid, as in [link].
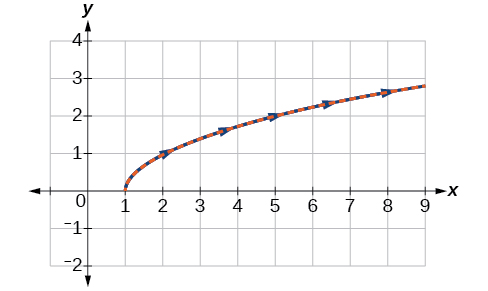
With the domain on
restricted, we only plot positive values of
The parametric data is graphed in blue and the graph of the rectangular equation is dashed in red. Once again, we see that the two forms overlap.
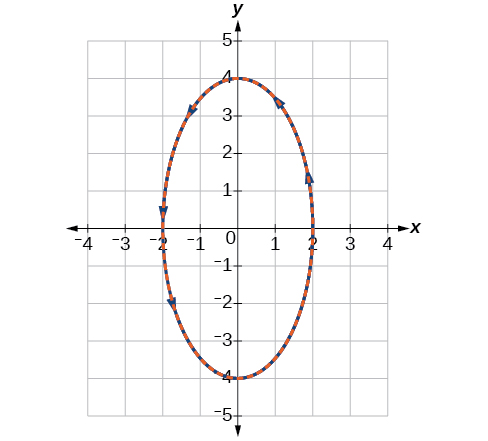
Sketch the graph of the parametric equations
along with the rectangular equation on the same grid.
The graph of the parametric equations is in red and the graph of the rectangular equation is drawn in blue dots on top of the parametric equations.
Many of the advantages of parametric equations become obvious when applied to solving real-world problems. Although rectangular equations in x and y give an overall picture of an object's path, they do not reveal the position of an object at a specific time. Parametric equations, however, illustrate how the values of x and y change depending on t, as the location of a moving object at a particular time.
A common application of parametric equations is solving problems involving projectile motion. In this type of motion, an object is propelled forward in an upward direction forming an angle of
to the horizontal, with an initial speed of
and at a height
above the horizontal.
The path of an object propelled at an inclination of
to the horizontal, with initial speed
and at a height
above the horizontal, is given by
where
accounts for the effects of gravity and
is the initial height of the object. Depending on the units involved in the problem, use
or
The equation for
gives horizontal distance, and the equation for
gives the vertical distance.
Given a projectile motion problem, use parametric equations to solve.
Substitute the initial speed of the object for
indicates the angle at which the object is propelled. Substitute that angle in degrees for
The term
represents the effect of gravity. Depending on units involved, use
or
Again, substitute the initial speed for
and the height at which the object was propelled for
Solve the problem presented at the beginning of this section. Does the batter hit the game-winning home run? Assume that the ball is hit with an initial velocity of 140 feet per second at an angle of
to the horizontal, making contact 3 feet above the ground.
Use the formulas to set up the equations. The horizontal position is found using the parametric equation for
Thus,
The vertical position is found using the parametric equation for
Thus,
Substitute 2 into the equations to find the horizontal and vertical positions of the ball.
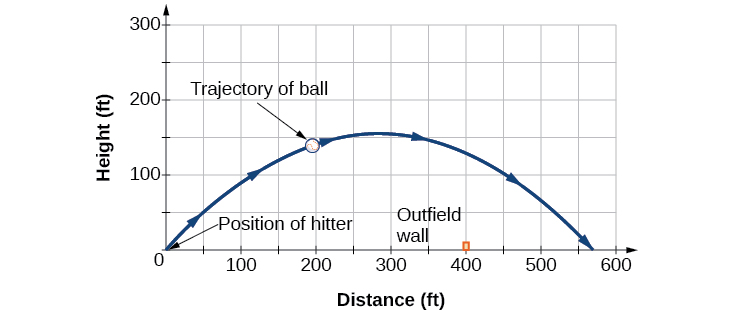
After 2 seconds, the ball is 198 feet away from the batter’s box and 137 feet above the ground.
To calculate how long the ball is in the air, we have to find out when it will hit ground, or when
Thus,
When
seconds, the ball has hit the ground. (The quadratic equation can be solved in various ways, but this problem was solved using a computer math program.)
We cannot confirm that the hit was a home run without considering the size of the outfield, which varies from field to field. However, for simplicity’s sake, let’s assume that the outfield wall is 400 feet from home plate in the deepest part of the park. Let’s also assume that the wall is 10 feet high. In order to determine whether the ball clears the wall, we need to calculate how high the ball is when x = 400 feet. So we will set x = 400, solve for
and input
into
The ball is 141.8 feet in the air when it soars out of the ballpark. It was indeed a home run. See [link].
Access the following online resource for additional instruction and practice with graphs of parametric equations.
and
depend, parametric equations can be used.
and
Choose values for
in increasing order. Plot the last two columns for
and
and
Initial velocity is symbolized as
represents the initial angle of the object when thrown, and
represents the height at which the object is propelled.
What are two methods used to graph parametric equations?
plotting points with the orientation arrow and a graphing calculator
What is one difference in point-plotting parametric equations compared to Cartesian equations?
Why are some graphs drawn with arrows?
The arrows show the orientation, the direction of motion according to increasing values of
Name a few common types of graphs of parametric equations.
Why are parametric graphs important in understanding projectile motion?
The parametric equations show the different vertical and horizontal motions over time.
For the following exercises, graph each set of parametric equations by making a table of values. Include the orientation on the graph.
For the following exercises, sketch the curve and include the orientation.
For the following exercises, graph the equation and include the orientation. Then, write the Cartesian equation.
For the following exercises, graph the equation and include the orientation.
For the following exercises, use the parametric equations for integers a and b:
Graph on the domain
where
and
and include the orientation.
Graph on the domain
where
and
, and include the orientation.
Graph on the domain
where
and
, and include the orientation.
Graph on the domain
where
and
, and include the orientation.
If
is 1 more than
describe the effect the values of
and
have on the graph of the parametric equations.
Describe the graph if
and
There will be 100 back-and-forth motions.
What happens if
is 1 more than
Describe the graph.
If the parametric equations
and
have the graph of a horizontal parabola opening to the right, what would change the direction of the curve?
Take the opposite of the
equation.
For the following exercises, describe the graph of the set of parametric equations.
and
is linear
and
is linear
The parabola opens up.
and
is linear
Write the parametric equations of a circle with center
radius 5, and a counterclockwise orientation.
Write the parametric equations of an ellipse with center
major axis of length 10, minor axis of length 6, and a counterclockwise orientation.
For the following exercises, use a graphing utility to graph on the window
by
on the domain
for the following values of
and
, and include the orientation.
For the following exercises, look at the graphs that were created by parametric equations of the form
Use the parametric mode on the graphing calculator to find the values of
and
to achieve each graph.
For the following exercises, use a graphing utility to graph the given parametric equations.
Graph all three sets of parametric equations on the domain
Graph all three sets of parametric equations on the domain
Graph all three sets of parametric equations on the domain
The graph of each set of parametric equations appears to “creep” along one of the axes. What controls which axis the graph creeps along?
Explain the effect on the graph of the parametric equation when we switched
and
.
The
-intercept changes.
Explain the effect on the graph of the parametric equation when we changed the domain.
An object is thrown in the air with vertical velocity of 20 ft/s and horizontal velocity of 15 ft/s. The object’s height can be described by the equation
, while the object moves horizontally with constant velocity 15 ft/s. Write parametric equations for the object’s position, and then eliminate time to write height as a function of horizontal position.
A skateboarder riding on a level surface at a constant speed of 9 ft/s throws a ball in the air, the height of which can be described by the equation
Write parametric equations for the ball’s position, and then eliminate time to write height as a function of horizontal position.
For the following exercises, use this scenario: A dart is thrown upward with an initial velocity of 65 ft/s at an angle of elevation of 52°. Consider the position of the dart at any time
Neglect air resistance.
Find parametric equations that model the problem situation.
Find all possible values of
that represent the situation.
When will the dart hit the ground?
approximately 3.2 seconds
Find the maximum height of the dart.
At what time will the dart reach maximum height?
1.6 seconds
For the following exercises, look at the graphs of each of the four parametric equations. Although they look unusual and beautiful, they are so common that they have names, as indicated in each exercise. Use a graphing utility to graph each on the indicated domain.
An epicycloid:
on the domain
.
A hypocycloid:
on the domain
.
A hypotrochoid:
on the domain
.
A rose:
on the domain
.

You can also download for free at http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@8.1
Attribution: