Solving Trigonometric Equations

In this section, you will:

Solve linear trigonometric equations in sine and cosine.
Solve equations involving a single trigonometric function.
Solve trigonometric equations using a calculator.
Solve trigonometric equations that are quadratic in form.
Solve trigonometric equations using fundamental identities.
Solve trigonometric equations with multiple angles.
Solve right triangle problems.

Photo of the Egyptian pyramids near a modern city.

Thales of Miletus (circa 625–547 BC) is known as the founder of geometry. The legend is that he calculated the height of the Great Pyramid of Giza in Egypt using the theory of similar triangles, which he developed by measuring the shadow of his staff. Based on proportions, this theory has applications in a number of areas, including fractal geometry, engineering, and architecture. Often, the angle of elevation and the angle of depression are found using similar triangles.

In earlier sections of this chapter, we looked at trigonometric identities. Identities are true for all values in the domain of the variable. In this section, we begin our study of trigonometric equations to study real-world scenarios such as the finding the dimensions of the pyramids.

Solving Linear Trigonometric Equations in Sine and Cosine

Trigonometric equations are, as the name implies, equations that involve trigonometric functions. Similar in many ways to solving polynomial equations or rational equations, only specific values of the variable will be solutions, if there are solutions at all. Often we will solve a trigonometric equation over a specified interval. However, just as often, we will be asked to find all possible solutions, and as trigonometric functions are periodic, solutions are repeated within each period. In other words, trigonometric equations may have an infinite number of solutions. Additionally, like rational equations, the domain of the function must be considered before we assume that any solution is valid. The period of both the sine function and the cosine function is $2 π .$

In other words, every $2 π$

units, the y-values repeat. If we need to find all possible solutions, then we must add $2 π k,$

where $k$

is an integer, to the initial solution. Recall the rule that gives the format for stating all possible solutions for a function where the period is $2 π :$

\sin θ = \sin (θ \pm 2 k π)

There are similar rules for indicating all possible solutions for the other trigonometric functions. Solving trigonometric equations requires the same techniques as solving algebraic equations. We read the equation from left to right, horizontally, like a sentence. We look for known patterns, factor, find common denominators, and substitute certain expressions with a variable to make solving a more straightforward process. However, with trigonometric equations, we also have the advantage of using the identities we developed in the previous sections.

Solving a Linear Trigonometric Equation Involving the Cosine Function

Find all possible exact solutions for the equation $\cos θ = \frac{1}{2} .$

From the unit circle, we know that

\begin{array}{l} \cos θ = \frac{1}{2} \\ θ = \frac{π}{3}, \frac{5 π}{3} \end{array}

These are the solutions in the interval $[0, 2 π] .$

All possible solutions are given by

\frac{π}{3} \pm 2 k π and \frac{5 π}{3} \pm 2 k π

where $k$

is an integer.

Solving a Linear Equation Involving the Sine Function

Find all possible exact solutions for the equation $\sin t = \frac{1}{2} .$

Solving for all possible values of t means that solutions include angles beyond the period of $2 π .$

From [link], we can see that the solutions are $\frac{π}{6}$

and $\frac{5 π}{6} .$

But the problem is asking for all possible values that solve the equation. Therefore, the answer is

\frac{π}{6} \pm 2 π k and \frac{5 π}{6} \pm 2 π k

where $k$

is an integer.

Given a trigonometric equation, solve using algebra.

Look for a pattern that suggests an algebraic property, such as the difference of squares or a factoring opportunity.
Substitute the trigonometric expression with a single variable, such as $x$
or
$u .$
Solve the equation the same way an algebraic equation would be solved.
Substitute the trigonometric expression back in for the variable in the resulting expressions.
Solve for the angle.

Solve the Trigonometric Equation in Linear Form

Solve the equation exactly: $2 \cos θ - 3 = - 5, 0 \leq θ < 2 π .$

Use algebraic techniques to solve the equation.

\begin{array}{l} 2 \cos θ - 3 = - 5 \\ 2 \cos θ = - 2 \\ \cos θ = - 1 \\ θ = π \end{array}

Solve exactly the following linear equation on the interval $[0, 2 π) : 2 \sin x + 1 = 0.$

x = \frac{7 π}{6}, \frac{11 π}{6}

Solving Equations Involving a Single Trigonometric Function

When we are given equations that involve only one of the six trigonometric functions, their solutions involve using algebraic techniques and the unit circle (see [link]). We need to make several considerations when the equation involves trigonometric functions other than sine and cosine. Problems involving the reciprocals of the primary trigonometric functions need to be viewed from an algebraic perspective. In other words, we will write the reciprocal function, and solve for the angles using the function. Also, an equation involving the tangent function is slightly different from one containing a sine or cosine function. First, as we know, the period of tangent is $π,$

not $2 π .$

Further, the domain of tangent is all real numbers with the exception of odd integer multiples of $\frac{π}{2},$

unless, of course, a problem places its own restrictions on the domain.

Solving a Problem Involving a Single Trigonometric Function

Solve the problem exactly: $2 \sin^{2} θ - 1 = 0, 0 \leq θ < 2 π .$

As this problem is not easily factored, we will solve using the square root property. First, we use algebra to isolate $\sin θ .$

Then we will find the angles.

\begin{array}{l} 2 \sin^{2} θ - 1 = 0 \\ 2 \sin^{2} θ = 1 \\ \sin^{2} θ = \frac{1}{2} \\ \sqrt{\sin^{2} θ} = \pm \sqrt{\frac{1}{2}} \\ \sin θ = \pm \frac{1}{\sqrt{2}} = \pm \frac{\sqrt{2}}{2} \\ θ = \frac{π}{4}, \frac{3 π}{4}, \frac{5 π}{4}, \frac{7 π}{4} \end{array}

Solving a Trigonometric Equation Involving Cosecant

Solve the following equation exactly: $\csc θ = - 2, 0 \leq θ < 4 π .$

We want all values of $θ$

for which $\csc θ = - 2$

over the interval $0 \leq θ < 4 π .$

\begin{array}{l} \csc θ = - 2 \\ \frac{1}{\sin θ} = - 2 \\ \sin θ = - \frac{1}{2} \\ θ = \frac{7 π}{6}, \frac{11 π}{6}, \frac{19 π}{6}, \frac{23 π}{6} \end{array}

Analysis

As $\sin θ = - \frac{1}{2},$

notice that all four solutions are in the third and fourth quadrants.

Solving an Equation Involving Tangent

Solve the equation exactly: $\tan (θ - \frac{π}{2}) = 1, 0 \leq θ < 2 π .$

Recall that the tangent function has a period of $π .$

On the interval $[0, π),$

and at the angle of $\frac{π}{4},$

the tangent has a value of 1. However, the angle we want is $(θ - \frac{π}{2}) .$

Thus, if $\tan (\frac{π}{4}) = 1,$

then

\begin{matrix} θ - \frac{π}{2} = \frac{π}{4} \\ θ = \frac{3 π}{4} \pm k π \end{matrix}

Over the interval $[0, 2 π),$

we have two solutions:

\frac{3 π}{4} and \frac{3 π}{4} + π = \frac{7 π}{4}

Find all solutions for $\tan x = \sqrt{3} .$

\frac{π}{3} \pm π k

Identify all Solutions to the Equation Involving Tangent

Identify all exact solutions to the equation $2 (\tan x + 3) = 5 + \tan x, 0 \leq x < 2 π .$

We can solve this equation using only algebra. Isolate the expression $\tan x$

on the left side of the equals sign.

\begin{matrix} 2 (\tan x) + 2 (3) & = 5 + \tan x \\ 2 \tan x + 6 & = 5 + \tan x \\ 2 \tan x - \tan x & = 5 - 6 \\ \tan x & = - 1 \end{matrix}

There are two angles on the unit circle that have a tangent value of $−1 : θ = \frac{3 π}{4}$

and $θ = \frac{7 π}{4} .$

Solve Trigonometric Equations Using a Calculator

Not all functions can be solved exactly using only the unit circle. When we must solve an equation involving an angle other than one of the special angles, we will need to use a calculator. Make sure it is set to the proper mode, either degrees or radians, depending on the criteria of the given problem.

Using a Calculator to Solve a Trigonometric Equation Involving Sine

Use a calculator to solve the equation $\sin θ = 0.8,$

where $θ$

is in radians.

Make sure mode is set to radians. To find $θ,$

use the inverse sine function. On most calculators, you will need to push the 2^ND button and then the SIN button to bring up the $\sin^{- 1}$

function. What is shown on the screen is $\sin^{- 1} (.$

The calculator is ready for the input within the parentheses. For this problem, we enter $\sin^{- 1} (0.8),$

and press ENTER. Thus, to four decimals places,

\sin^{- 1} (0.8) \approx 0.9273

The solution is

0.9273 \pm 2 π k

The angle measurement in degrees is

\begin{array}{l} \begin{array}{l} θ \approx {53.1}^{\circ} \end{array} \\ θ \approx 180^{\circ} - {53.1}^{\circ} \\ \approx {126.9}^{\circ} \end{array}

Analysis

Note that a calculator will only return an angle in quadrants I or IV for the sine function, since that is the range of the inverse sine. The other angle is obtained by using $π - θ .$

Using a Calculator to Solve a Trigonometric Equation Involving Secant

Use a calculator to solve the equation $\sec θ = −4,$

giving your answer in radians.

We can begin with some algebra.

\begin{matrix} \sec θ = - 4 \\ \frac{1}{\cos θ} = - 4 \\ \cos θ = - \frac{1}{4} \end{matrix}

Check that the MODE is in radians. Now use the inverse cosine function.

\begin{array}{l} \cos^{- 1} (- \frac{1}{4}) \approx 1.8235 \\ θ \approx 1.8235 + 2 π k \end{array}

Since $\frac{π}{2} \approx 1.57$

and $π \approx 3.14,$

1.8235 is between these two numbers, thus $θ \approx 1 .8235$

is in quadrant II. Cosine is also negative in quadrant III. Note that a calculator will only return an angle in quadrants I or II for the cosine function, since that is the range of the inverse cosine. See [link].

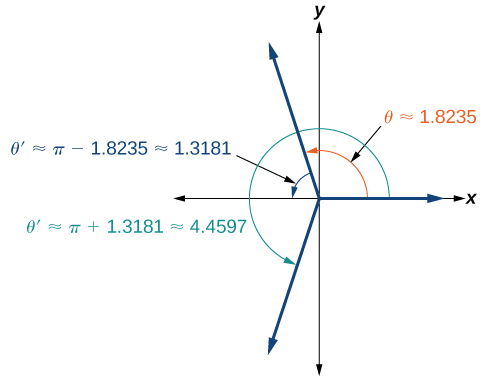
Graph of angles theta =approx 1.8235, theta prime =approx pi - 1.8235 = approx 1.3181, and then theta prime = pi + 1.3181 = approx 4.4597

So, we also need to find the measure of the angle in quadrant III. In quadrant III, the reference angle is $θ ' \approx π - 1 .8235 \approx 1 .3181 .$

The other solution in quadrant III is $π + 1 .3181 \approx 4 .4597 .$

The solutions are $1.8235 \pm 2 π k$

and $4.4597 \pm 2 π k .$

Solve $\cos θ = - 0.2.$

θ \approx 1.7722 \pm 2 π k

and $θ \approx 4.5110 \pm 2 π k$

Solving Trigonometric Equations in Quadratic Form

Solving a quadratic equation may be more complicated, but once again, we can use algebra as we would for any quadratic equation. Look at the pattern of the equation. Is there more than one trigonometric function in the equation, or is there only one? Which trigonometric function is squared? If there is only one function represented and one of the terms is squared, think about the standard form of a quadratic. Replace the trigonometric function with a variable such as $x$

or $u .$

If substitution makes the equation look like a quadratic equation, then we can use the same methods for solving quadratics to solve the trigonometric equations.

Solving a Trigonometric Equation in Quadratic Form

Solve the equation exactly: $\cos^{2} θ + 3 \cos θ - 1 = 0, 0 \leq θ < 2 π .$

We begin by using substitution and replacing cos $θ$

with $x .$

It is not necessary to use substitution, but it may make the problem easier to solve visually. Let $\cos θ = x .$

We have

x^{2} + 3 x - 1 = 0

The equation cannot be factored, so we will use the quadratic formula $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a} .$

\begin{array}{l} x = \frac{- 3 \pm \sqrt{{(3)}^{2} - 4 (1) (- 1)}}{2} \\ = \frac{- 3 \pm \sqrt{13}}{2} \end{array}

Replace $x$

with $\cos θ,$

and solve. Thus,

\begin{array}{l} \cos θ = \frac{- 3 \pm \sqrt{13}}{2} \\ θ = \cos^{- 1} (\frac{- 3 + \sqrt{13}}{2}) \end{array}

Note that only the + sign is used. This is because we get an error when we solve $θ = \cos^{- 1} (\frac{- 3 - \sqrt{13}}{2})$

on a calculator, since the domain of the inverse cosine function is $[- 1, 1] .$

However, there is a second solution:

\begin{array}{l} \cos^{- 1} (\frac{- 3 + \sqrt{13}}{2}) \\ \approx 1.26 \end{array}

This terminal side of the angle lies in quadrant I. Since cosine is also positive in quadrant IV, the second solution is

\begin{array}{l} 2 π - \cos^{- 1} (\frac{- 3 + \sqrt{13}}{2}) \\ \approx 5.02 \end{array}

Solving a Trigonometric Equation in Quadratic Form by Factoring

Solve the equation exactly: $2 \sin^{2} θ - 5 \sin θ + 3 = 0, 0 \leq θ \leq 2 π .$

Using grouping, this quadratic can be factored. Either make the real substitution, $\sin θ = u,$

or imagine it, as we factor:

\begin{array}{l} 2 \sin^{2} θ - 5 \sin θ + 3 = 0 \\ (2 \sin θ - 3) (\sin θ - 1) = 0 \end{array}

Now set each factor equal to zero.

\begin{array}{l} 2 \sin θ - 3 = 0 \\ 2 \sin θ = 3 \\ \sin θ = \frac{3}{2} \\ \sin θ - 1 = 0 \\ \sin θ = 1 \end{array}

Next solve for $θ : \sin θ \neq \frac{3}{2},$

as the range of the sine function is $[−1, 1] .$

However, $\sin θ = 1,$

giving the solution $\frac{π}{2} .$

Analysis

Make sure to check all solutions on the given domain as some factors have no solution.

Solve $\sin^{2} θ = 2 \cos θ + 2, 0 \leq θ \leq 2 π .$

[Hint: Make a substitution to express the equation only in terms of cosine.]

\cos θ = - 1, θ = π

Solving a Trigonometric Equation Using Algebra

Solve exactly:

2 \sin^{2} θ + \sin θ = 0; 0 \leq θ < 2 π

This problem should appear familiar as it is similar to a quadratic. Let $\sin θ = x .$

The equation becomes $2 x^{2} + x = 0.$

We begin by factoring:

\begin{array}{l} 2 x^{2} + x = 0 \\ x (2 x + 1) = 0 \end{array}

Set each factor equal to zero.

\begin{array}{l} x = 0 \\ (2 x + 1) = 0 \\ x = - \frac{1}{2} \end{array}

Then, substitute back into the equation the original expression $\sin θ$

for $x .$

Thus,

\begin{array}{l} \sin θ = 0 \\ θ = 0, π \\ \sin θ = - \frac{1}{2} \\ θ = \frac{7 π}{6}, \frac{11 π}{6} \end{array}

The solutions within the domain $0 \leq θ < 2 π$

are $0, π, \frac{7 π}{6}, \frac{11 π}{6} .$

If we prefer not to substitute, we can solve the equation by following the same pattern of factoring and setting each factor equal to zero.

\begin{array}{l} 2 \sin^{2} θ + \sin θ = 0 \\ \sin θ (2 \sin θ + 1) = 0 \\ \sin θ = 0 \\ θ = 0, π \\ 2 \sin θ + 1 = 0 \\ 2 \sin θ = - 1 \\ \sin θ = - \frac{1}{2} \\ θ = \frac{7 π}{6}, \frac{11 π}{6} \end{array}

Analysis

We can see the solutions on the graph in [link]. On the interval $0 \leq θ < 2 π,$

the graph crosses the x-axis four times, at the solutions noted. Notice that trigonometric equations that are in quadratic form can yield up to four solutions instead of the expected two that are found with quadratic equations. In this example, each solution (angle) corresponding to a positive sine value will yield two angles that would result in that value.

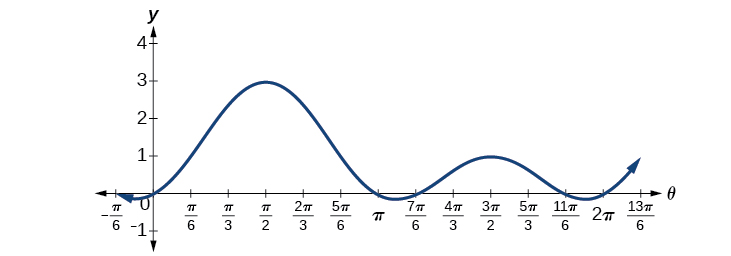
Graph of 2*(sin(theta))^2 + sin(theta) from 0 to 2pi. Zeros are at 0, pi, 7pi/6, and 11pi/6.

We can verify the solutions on the unit circle in [link] as well.

Solving a Trigonometric Equation Quadratic in Form

Solve the equation quadratic in form exactly: $2 \sin^{2} θ - 3 \sin θ + 1 = 0, 0 \leq θ < 2 π .$

We can factor using grouping. Solution values of $θ$

can be found on the unit circle:

\begin{array}{l} (2 \sin θ - 1) (\sin θ - 1) = 0 \\ 2 \sin θ - 1 = 0 \\ \sin θ = \frac{1}{2} \\ θ = \frac{π}{6}, \frac{5 π}{6} \\ \sin θ = 1 \\ θ = \frac{π}{2} \end{array}

Solve the quadratic equation $2 \cos^{2} θ + \cos θ = 0.$

\frac{π}{2}, \frac{2 π}{3}, \frac{4 π}{3}, \frac{3 π}{2}

Solving Trigonometric Equations Using Fundamental Identities

While algebra can be used to solve a number of trigonometric equations, we can also use the fundamental identities because they make solving equations simpler. Remember that the techniques we use for solving are not the same as those for verifying identities. The basic rules of algebra apply here, as opposed to rewriting one side of the identity to match the other side. In the next example, we use two identities to simplify the equation.

Use Identities to Solve an Equation

Use identities to solve exactly the trigonometric equation over the interval $0 \leq x < 2 π .$

\cos x \cos (2 x) + \sin x \sin (2 x) = \frac{\sqrt{3}}{2}

Notice that the left side of the equation is the difference formula for cosine.

\begin{array}{l} \cos x \cos (2 x) + \sin x \sin (2 x) = \frac{\sqrt{3}}{2} \\ \cos (x - 2 x) = \frac{\sqrt{3}}{2} \begin{matrix}  \end{matrix} & Difference formula for cosine \\ \cos (- x) = \frac{\sqrt{3}}{2} & Use the negative angle identity . \\ \cos x = \frac{\sqrt{3}}{2} \end{array}

From the unit circle in [link], we see that $\cos x = \frac{\sqrt{3}}{2}$

when $x = \frac{π}{6}, \frac{11 π}{6} .$

Solving the Equation Using a Double-Angle Formula

Solve the equation exactly using a double-angle formula: $\cos (2 θ) = \cos θ .$

We have three choices of expressions to substitute for the double-angle of cosine. As it is simpler to solve for one trigonometric function at a time, we will choose the double-angle identity involving only cosine:

\begin{array}{l} \cos (2 θ) = \cos θ \\ 2 \cos^{2} θ - 1 = \cos θ \\ 2 \cos^{2} θ - \cos θ - 1 = 0 \\ (2 \cos θ + 1) (\cos θ - 1) = 0 \\ 2 \cos θ + 1 = 0 \\ \cos θ = - \frac{1}{2} \\ \cos θ - 1 = 0 \\ \cos θ = 1 \end{array}

So, if $\cos θ = - \frac{1}{2},$

then $θ = \frac{2 π}{3} \pm 2 π k$

and $θ = \frac{4 π}{3} \pm 2 π k;$

if $\cos θ = 1,$

then $θ = 0 \pm 2 π k .$

Solving an Equation Using an Identity

Solve the equation exactly using an identity: $3 \cos θ + 3 = 2 \sin^{2} θ, 0 \leq θ < 2 π .$

If we rewrite the right side, we can write the equation in terms of cosine:

\begin{matrix} 3 cos θ + 3 & = {2 sin}^{2} θ \\ 3 cos θ + 3 & = 2 (1 - {cos}^{2} θ) \\ 3 cos θ + 3 & = 2 - 2 \cos^{2} θ \\ 2 \cos^{2} θ + 3 cos θ + 1 & = 0 \\ (2 cos θ + 1) (\cos θ + 1) & = 0 \\ 2 cos θ + 1 & = 0 \\ \cos θ & = - \frac{1}{2} \\ θ & = \frac{2 π}{3}, \frac{4 π}{3} \\ \cos θ + 1 & = 0 \\ \cos θ & = - 1 \\ θ & = π \end{matrix}

Our solutions are $\frac{2 π}{3}, \frac{4 π}{3}, π .$

Solving Trigonometric Equations with Multiple Angles

Sometimes it is not possible to solve a trigonometric equation with identities that have a multiple angle, such as $\sin (2 x)$

or $\cos (3 x) .$

When confronted with these equations, recall that $y = \sin (2 x)$

is a horizontal compression by a factor of 2 of the function $y = \sin x .$

On an interval of $2 π,$

we can graph two periods of $y = \sin (2 x),$

as opposed to one cycle of $y = \sin x .$

This compression of the graph leads us to believe there may be twice as many x-intercepts or solutions to $\sin (2 x) = 0$

compared to $\sin x = 0.$

This information will help us solve the equation.

Solving a Multiple Angle Trigonometric Equation

Solve exactly: $\cos (2 x) = \frac{1}{2}$

on $[0, 2 π) .$

We can see that this equation is the standard equation with a multiple of an angle. If $\cos (α) = \frac{1}{2},$

we know $α$

is in quadrants I and IV. While $θ = \cos^{- 1} \frac{1}{2}$

will only yield solutions in quadrants I and II, we recognize that the solutions to the equation $\cos θ = \frac{1}{2}$

will be in quadrants I and IV.

Therefore, the possible angles are $θ = \frac{π}{3}$

and $θ = \frac{5 π}{3} .$

So, $2 x = \frac{π}{3}$

or $2 x = \frac{5 π}{3},$

which means that $x = \frac{π}{6}$

or $x = \frac{5 π}{6} .$

Does this make sense? Yes, because $\cos (2 (\frac{π}{6})) = \cos (\frac{π}{3}) = \frac{1}{2} .$

Are there any other possible answers? Let us return to our first step.

In quadrant I, $2 x = \frac{π}{3},$

so $x = \frac{π}{6}$

as noted. Let us revolve around the circle again:

\begin{array}{l} 2 x = \frac{π}{3} + 2 π \\ = \frac{π}{3} + \frac{6 π}{3} \\ = \frac{7 π}{3} \end{array}

so $x = \frac{7 π}{6} .$

One more rotation yields

\begin{array}{l} \begin{array}{l} 2 x = \frac{π}{3} + 4 π \end{array} \\ = \frac{π}{3} + \frac{12 π}{3} \\ = \frac{13 π}{3} \end{array}

x = \frac{13 π}{6} > 2 π,

so this value for $x$

is larger than $2 π,$

so it is not a solution on $[0, 2 π) .$

In quadrant IV, $2 x = \frac{5 π}{3},$

so $x = \frac{5 π}{6}$

as noted. Let us revolve around the circle again:

\begin{array}{l} 2 x = \frac{5 π}{3} + 2 π \\ = \frac{5 π}{3} + \frac{6 π}{3} \\ = \frac{11 π}{3} \end{array}

so $x = \frac{11 π}{6} .$

One more rotation yields

\begin{array}{l} 2 x = \frac{5 π}{3} + 4 π \\ = \frac{5 π}{3} + \frac{12 π}{3} \\ = \frac{17 π}{3} \end{array}

x = \frac{17 π}{6} > 2 π,

so this value for $x$

is larger than $2 π,$

so it is not a solution on $[0, 2 π) .$

Our solutions are $\frac{π}{6}, \frac{5 π}{6}, \frac{7 π}{6}, and \frac{11 π}{6} .$

Note that whenever we solve a problem in the form of $\sin (n x) = c,$

we must go around the unit circle $n$

times.

Solving Right Triangle Problems

We can now use all of the methods we have learned to solve problems that involve applying the properties of right triangles and the Pythagorean Theorem. We begin with the familiar Pythagorean Theorem, $a^{2} + b^{2} = c^{2},$

and model an equation to fit a situation.

Using the Pythagorean Theorem to Model an Equation

Use the Pythagorean Theorem, and the properties of right triangles to model an equation that fits the problem.

One of the cables that anchors the center of the London Eye Ferris wheel to the ground must be replaced. The center of the Ferris wheel is 69.5 meters above the ground, and the second anchor on the ground is 23 meters from the base of the Ferris wheel. Approximately how long is the cable, and what is the angle of elevation (from ground up to the center of the Ferris wheel)? See [link].

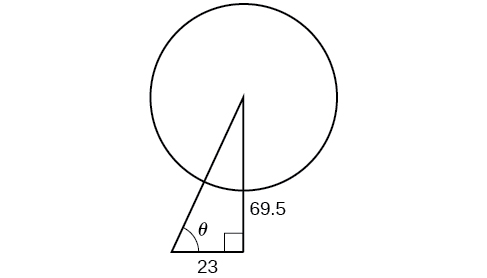
Using the information given, we can draw a right triangle. We can find the length of the cable with the Pythagorean Theorem.

\begin{array}{l} \begin{array}{l} \begin{array}{l} a^{2} + b^{2} = c^{2} \end{array} \\ {(23)}^{2} + {(69.5)}^{2} \approx 5359 \\ \sqrt{5359} \approx 73.2 m \end{array} \end{array}

The angle of elevation is $θ,$

formed by the second anchor on the ground and the cable reaching to the center of the wheel. We can use the tangent function to find its measure. Round to two decimal places.

\begin{array}{l} \tan θ = \frac{69.5}{23} \\ \tan^{- 1} (\frac{69.5}{23}) \approx 1.2522 \\ \approx {71.69}^{\circ} \end{array}

The angle of elevation is approximately ${71.7}^{\circ},$

and the length of the cable is 73.2 meters.

Using the Pythagorean Theorem to Model an Abstract Problem

OSHA safety regulations require that the base of a ladder be placed 1 foot from the wall for every 4 feet of ladder length. Find the angle that a ladder of any length forms with the ground and the height at which the ladder touches the wall.

For any length of ladder, the base needs to be a distance from the wall equal to one fourth of the ladder’s length. Equivalently, if the base of the ladder is “a” feet from the wall, the length of the ladder will be 4a feet. See [link].

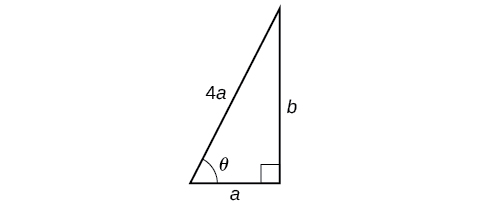
Diagram of a right triangle with base length a, height length b, hypotenuse length 4a. Opposite the height is an angle of theta degrees, and opposite the hypotenuse is an angle of 90 degrees.

The side adjacent to $θ$

is a and the hypotenuse is $4 a .$

Thus,

\begin{array}{l} \cos θ = \frac{a}{4 a} = \frac{1}{4} \\ \cos^{- 1} (\frac{1}{4}) \approx {75.5}^{\circ} \end{array}

The elevation of the ladder forms an angle of ${75.5}^{\circ}$

with the ground. The height at which the ladder touches the wall can be found using the Pythagorean Theorem:

\begin{array}{l} a^{2} + b^{2} = {(4 a)}^{2} \\ b^{2} = {(4 a)}^{2} - a^{2} \\ b^{2} = 16 a^{2} - a^{2} \\ b^{2} = 15 a^{2} \\ b = \sqrt{15} a \end{array}

Thus, the ladder touches the wall at $\sqrt{15} a$

feet from the ground.

Access these online resources for additional instruction and practice with solving trigonometric equations.

Key Concepts

When solving linear trigonometric equations, we can use algebraic techniques just as we do solving algebraic equations. Look for patterns, like the difference of squares, quadratic form, or an expression that lends itself well to substitution. See [link], [link], and [link].
Equations involving a single trigonometric function can be solved or verified using the unit circle. See [link], [link], and [link], and [link].
We can also solve trigonometric equations using a graphing calculator. See [link] and [link].
Many equations appear quadratic in form. We can use substitution to make the equation appear simpler, and then use the same techniques we use solving an algebraic quadratic: factoring, the quadratic formula, etc. See [link], [link], [link], and [link].
We can also use the identities to solve trigonometric equation. See [link], [link], and [link].
We can use substitution to solve a multiple-angle trigonometric equation, which is a compression of a standard trigonometric function. We will need to take the compression into account and verify that we have found all solutions on the given interval. See [link].
Real-world scenarios can be modeled and solved using the Pythagorean Theorem and trigonometric functions. See [link].

Section Exercises

Verbal

Will there always be solutions to trigonometric function equations? If not, describe an equation that would not have a solution. Explain why or why not.

There will not always be solutions to trigonometric function equations. For a basic example, $\cos (x) = −5.$

When solving a trigonometric equation involving more than one trig function, do we always want to try to rewrite the equation so it is expressed in terms of one trigonometric function? Why or why not?

When solving linear trig equations in terms of only sine or cosine, how do we know whether there will be solutions?

If the sine or cosine function has a coefficient of one, isolate the term on one side of the equals sign. If the number it is set equal to has an absolute value less than or equal to one, the equation has solutions, otherwise it does not. If the sine or cosine does not have a coefficient equal to one, still isolate the term but then divide both sides of the equation by the leading coefficient. Then, if the number it is set equal to has an absolute value greater than one, the equation has no solution.

Algebraic

For the following exercises, find all solutions exactly on the interval $0 \leq θ < 2 π .$

2 \sin θ = − \sqrt{2}

2 \sin θ = \sqrt{3}

\frac{π}{3}, \frac{2 π}{3}

2 \cos θ = 1

2 \cos θ = − \sqrt{2}

\frac{3 π}{4}, \frac{5 π}{4}

\tan θ = −1

\tan x = 1

\frac{π}{4}, \frac{5 π}{4}

\cot x + 1 = 0

4 \sin^{2} x - 2 = 0

\frac{π}{4}, \frac{3 π}{4}, \frac{5 π}{4}, \frac{7 π}{4}

\csc^{2} x - 4 = 0

For the following exercises, solve exactly on $[0, 2 π) .$

2 \cos θ = \sqrt{2}

\frac{π}{4}, \frac{7 π}{4}

2 \cos θ = −1

2 \sin θ = −1

\frac{7 π}{6}, \frac{11 π}{6}

2 \sin θ = − \sqrt{3}

2 \sin (3 θ) = 1

\frac{π}{18}, \frac{5 π}{18}, \frac{13 π}{18}, \frac{17 π}{18}, \frac{25 π}{18}, \frac{29 π}{18}

2 \sin (2 θ) = \sqrt{3}

2 \cos (3 θ) = - \sqrt{2}

\frac{3 π}{12}, \frac{5 π}{12}, \frac{11 π}{12}, \frac{13 π}{12}, \frac{19 π}{12}, \frac{21 π}{12}

\cos (2 θ) = - \frac{\sqrt{3}}{2}

2 \sin (π θ) = 1

\frac{1}{6}, \frac{5}{6}, \frac{13}{6}, \frac{17}{6}, \frac{25}{6}, \frac{29}{6}, \frac{37}{6}

2 \cos (\frac{π}{5} θ) = \sqrt{3}

For the following exercises, find all exact solutions on $[0, 2 π) .$

\sec (x) \sin (x) - 2 \sin (x) = 0

0, \frac{π}{3}, π, \frac{5 π}{3}

\tan (x) - 2 \sin (x) \tan (x) = 0

2 \cos^{2} t + \cos (t) = 1

\frac{π}{3}, π, \frac{5 π}{3}

2 \tan^{2} (t) = 3 \sec (t)

2 \sin (x) \cos (x) - \sin (x) + 2 \cos (x) - 1 = 0

\frac{π}{3}, \frac{3 π}{2}, \frac{5 π}{3}

\cos^{2} θ = \frac{1}{2}

\sec^{2} x = 1

0, π

\tan^{2} (x) = - 1 + 2 \tan (- x)

8 \sin^{2} (x) + 6 \sin (x) + 1 = 0

π - \sin^{- 1} (- \frac{1}{4}), \frac{7 π}{6}, \frac{11 π}{6}, 2 π + \sin^{- 1} (- \frac{1}{4})

\tan^{5} (x) = \tan (x)

For the following exercises, solve with the methods shown in this section exactly on the interval $[0, 2 π) .$

\sin (3 x) \cos (6 x) - \cos (3 x) \sin (6 x) = −0.9

\frac{1}{3} (\sin^{- 1} (\frac{9}{10})), \frac{π}{3} - \frac{1}{3} (\sin^{- 1} (\frac{9}{10})), \frac{2 π}{3} + \frac{1}{3} (\sin^{- 1} (\frac{9}{10})), π - \frac{1}{3} (\sin^{- 1} (\frac{9}{10})), \frac{4 π}{3} + \frac{1}{3} (\sin^{- 1} (\frac{9}{10})), \frac{5 π}{3} - \frac{1}{3} (\sin^{- 1} (\frac{9}{10}))

\sin (6 x) \cos (11 x) - \cos (6 x) \sin (11 x) = −0.1

\cos (2 x) \cos x + \sin (2 x) \sin x = 1

0

6 \sin (2 t) + 9 \sin t = 0

9 \cos (2 θ) = 9 \cos^{2} θ - 4

\frac{π}{6}, \frac{5 π}{6}, \frac{7 π}{6}, \frac{11 π}{6}

\sin (2 t) = \cos t

\cos (2 t) = \sin t

\frac{3 π}{2}, \frac{π}{6}, \frac{5 π}{6}

\cos (6 x) - \cos (3 x) = 0

For the following exercises, solve exactly on the interval $[0, 2 π) .$

Use the quadratic formula if the equations do not factor.

\tan^{2} x - \sqrt{3} \tan x = 0

0, \frac{π}{3}, π, \frac{4 π}{3}

\sin^{2} x + \sin x - 2 = 0

\sin^{2} x - 2 \sin x - 4 = 0

There are no solutions.

5 \cos^{2} x + 3 \cos x - 1 = 0

3 \cos^{2} x - 2 \cos x - 2 = 0

\cos^{- 1} (\frac{1}{3} (1 - \sqrt{7})), 2 π - \cos^{- 1} (\frac{1}{3} (1 - \sqrt{7}))

5 \sin^{2} x + 2 \sin x - 1 = 0

\tan^{2} x + 5 \tan x - 1 = 0

\tan^{- 1} (\frac{1}{2} (\sqrt{29} - 5)), π + \tan^{- 1} (\frac{1}{2} (- \sqrt{29} - 5)), π + \tan^{- 1} (\frac{1}{2} (\sqrt{29} - 5)), 2 π + \tan^{- 1} (\frac{1}{2} (- \sqrt{29} - 5))

\cot^{2} x = - \cot x

- \tan^{2} x - \tan x - 2 = 0

There are no solutions.

For the following exercises, find exact solutions on the interval $[0, 2 π) .$

Look for opportunities to use trigonometric identities.

\sin^{2} x - \cos^{2} x - \sin x = 0

\sin^{2} x + \cos^{2} x = 0

There are no solutions.

\sin (2 x) - \sin x = 0

\cos (2 x) - \cos x = 0

0, \frac{2 π}{3}, \frac{4 π}{3}

\frac{2 \tan x}{2 - \sec^{2} x} - \sin^{2} x = \cos^{2} x

1 - \cos (2 x) = 1 + \cos (2 x)

\frac{π}{4}, \frac{3 π}{4}, \frac{5 π}{4}, \frac{7 π}{4}

\sec^{2} x = 7

10 \sin x \cos x = 6 \cos x

\sin^{- 1} (\frac{3}{5}), \frac{π}{2}, π - \sin^{- 1} (\frac{3}{5}), \frac{3 π}{2}

−3 \sin t = 15 \cos t \sin t

4 \cos^{2} x - 4 = 15 \cos x

\cos^{- 1} (- \frac{1}{4}), 2 π - \cos^{- 1} (- \frac{1}{4})

8 \sin^{2} x + 6 \sin x + 1 = 0

8 \cos^{2} θ = 3 - 2 \cos θ

\frac{π}{3}, \cos^{- 1} (- \frac{3}{4}), 2 π - \cos^{- 1} (- \frac{3}{4}), \frac{5 π}{3}

6 \cos^{2} x + 7 \sin x - 8 = 0

12 \sin^{2} t + \cos t - 6 = 0

\cos^{- 1} (\frac{3}{4}), \cos^{- 1} (- \frac{2}{3}), 2 π - \cos^{- 1} (- \frac{2}{3}), 2 π - \cos^{- 1} (\frac{3}{4})

\tan x = 3 \sin x

\cos^{3} t = \cos t

0, \frac{π}{2}, π, \frac{3 π}{2}

Graphical

For the following exercises, algebraically determine all solutions of the trigonometric equation exactly, then verify the results by graphing the equation and finding the zeros.

6 \sin^{2} x - 5 \sin x + 1 = 0

8 \cos^{2} x - 2 \cos x - 1 = 0

\frac{π}{3}, \cos^{−1} (- \frac{1}{4}), 2 π - \cos^{−1} (- \frac{1}{4}), \frac{5 π}{3}

100 \tan^{2} x + 20 \tan x - 3 = 0

2 \cos^{2} x - \cos x + 15 = 0

There are no solutions.

20 \sin^{2} x - 27 \sin x + 7 = 0

2 \tan^{2} x + 7 \tan x + 6 = 0

π + \tan^{−1} (−2), π + \tan^{−1} (- \frac{3}{2}), 2 π + \tan^{−1} (−2), 2 π + \tan^{−1} (- \frac{3}{2})

130 \tan^{2} x + 69 \tan x - 130 = 0

Technology

For the following exercises, use a calculator to find all solutions to four decimal places.

\sin x = 0.27

2 π k + 0.2734, 2 π k + 2.8682

\sin x = −0.55

\tan x = −0.34

π k - 0.3277

\cos x = 0.71

For the following exercises, solve the equations algebraically, and then use a calculator to find the values on the interval $[0, 2 π) .$

Round to four decimal places.

\tan^{2} x + 3 \tan x - 3 = 0

0.6694, 1.8287, 3.8110, 4.9703

6 \tan^{2} x + 13 \tan x = −6

\tan^{2} x - \sec x = 1

1.0472, 3.1416, 5.2360

\sin^{2} x - 2 \cos^{2} x = 0

2 \tan^{2} x + 9 \tan x - 6 = 0

0.5326, 1.7648, 3.6742, 4.9064

4 \sin^{2} x + \sin (2 x) \sec x - 3 = 0

Extensions

For the following exercises, find all solutions exactly to the equations on the interval $[0, 2 π) .$

\csc^{2} x - 3 \csc x - 4 = 0

\sin^{- 1} (\frac{1}{4}), π - \sin^{- 1} (\frac{1}{4}), \frac{3 π}{2}

\sin^{2} x - \cos^{2} x - 1 = 0

\sin^{2} x (1 - \sin^{2} x) + \cos^{2} x (1 - \sin^{2} x) = 0

\frac{π}{2}, \frac{3 π}{2}

3 \sec^{2} x + 2 + \sin^{2} x - \tan^{2} x + \cos^{2} x = 0

\sin^{2} x - 1 + 2 \cos (2 x) - \cos^{2} x = 1

There are no solutions.

\tan^{2} x - 1 - \sec^{3} x \cos x = 0

\frac{\sin (2 x)}{\sec^{2} x} = 0

0, \frac{π}{2}, π, \frac{3 π}{2}

\frac{\sin (2 x)}{2 \csc^{2} x} = 0

2 \cos^{2} x - \sin^{2} x - \cos x - 5 = 0

There are no solutions.

\frac{1}{\sec^{2} x} + 2 + \sin^{2} x + 4 \cos^{2} x = 4

Real-World Applications

An airplane has only enough gas to fly to a city 200 miles northeast of its current location. If the pilot knows that the city is 25 miles north, how many degrees north of east should the airplane fly?

{7.2}^{\circ}

If a loading ramp is placed next to a truck, at a height of 4 feet, and the ramp is 15 feet long, what angle does the ramp make with the ground?

If a loading ramp is placed next to a truck, at a height of 2 feet, and the ramp is 20 feet long, what angle does the ramp make with the ground?

{5.7}^{\circ}

A woman is watching a launched rocket currently 11 miles in altitude. If she is standing 4 miles from the launch pad, at what angle is she looking up from horizontal?

An astronaut is in a launched rocket currently 15 miles in altitude. If a man is standing 2 miles from the launch pad, at what angle is she looking down at him from horizontal? (Hint: this is called the angle of depression.)

{82.4}^{\circ}

A woman is standing 8 meters away from a 10-meter tall building. At what angle is she looking to the top of the building?

A man is standing 10 meters away from a 6-meter tall building. Someone at the top of the building is looking down at him. At what angle is the person looking at him?

{31.0}^{\circ}

A 20-foot tall building has a shadow that is 55 feet long. What is the angle of elevation of the sun?

A 90-foot tall building has a shadow that is 2 feet long. What is the angle of elevation of the sun?

{88.7}^{\circ}

A spotlight on the ground 3 meters from a 2-meter tall man casts a 6 meter shadow on a wall 6 meters from the man. At what angle is the light?

A spotlight on the ground 3 feet from a 5-foot tall woman casts a 15-foot tall shadow on a wall 6 feet from the woman. At what angle is the light?

{59.0}^{\circ}

For the following exercises, find a solution to the word problem algebraically. Then use a calculator to verify the result. Round the answer to the nearest tenth of a degree.

A person does a handstand with his feet touching a wall and his hands 1.5 feet away from the wall. If the person is 6 feet tall, what angle do his feet make with the wall?

A person does a handstand with her feet touching a wall and her hands 3 feet away from the wall. If the person is 5 feet tall, what angle do her feet make with the wall?

{36.9}^{\circ}

A 23-foot ladder is positioned next to a house. If the ladder slips at 7 feet from the house when there is not enough traction, what angle should the ladder make with the ground to avoid slipping?

This work is licensed under a Creative Commons Attribution 4.0 International License.

You can also download for free at http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@8.1

Attribution:

For questions regarding this license, please contact partners@openstaxcollege.org.
If you use this textbook as a bibliographic reference, then you should cite it as follows: OpenStax College, Precalculus. OpenStax CNX. http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@8.1.
If you redistribute this textbook in a print format, then you must include on every physical page the following attribution: "Download for free at http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@8.1."
If you redistribute part of this textbook, then you must retain in every digital format page view (including but not limited to EPUB, PDF, and HTML) and on every physical printed page the following attribution: "Download for free at http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@8.1."