Dividing Polynomials

In this section, you will:

Use long division to divide polynomials.
Use synthetic division to divide polynomials.

Lincoln Memorial.

The exterior of the Lincoln Memorial in Washington, D.C., is a large rectangular solid with length 61.5 meters (m), width 40 m, and height 30 m.¹ We can easily find the volume using elementary geometry.

\begin{array}{l} V = l \cdot w \cdot h \\ = 61.5 \cdot 40 \cdot 30 \\ = 73,800 \end{array}

So the volume is 73,800 cubic meters $(m ³) .$

Suppose we knew the volume, length, and width. We could divide to find the height.

\begin{array}{l} h = \frac{V}{l \cdot w} \\ = \frac{73, 800}{61.5 \cdot 40} \\ = 30 \end{array}

As we can confirm from the dimensions above, the height is 30 m. We can use similar methods to find any of the missing dimensions. We can also use the same method if any or all of the measurements contain variable expressions. For example, suppose the volume of a rectangular solid is given by the polynomial $3 x^{4} - 3 x^{3} - 33 x^{2} + 54 x .$

The length of the solid is given by $3 x;$

the width is given by $x - 2.$

To find the height of the solid, we can use polynomial division, which is the focus of this section.

Using Long Division to Divide Polynomials

We are familiar with the long division algorithm for ordinary arithmetic. We begin by dividing into the digits of the dividend that have the greatest place value. We divide, multiply, subtract, include the digit in the next place value position, and repeat. For example, let’s divide 178 by 3 using long division.

Steps of long division for intergers. Another way to look at the solution is as a sum of parts. This should look familiar, since it is the same method used to check division in elementary arithmetic.

\begin{array}{l} dividend = (divisor \cdot quotient) + remainder \\ 178 = (3 \cdot 59) + 1 \\ = 177 + 1 \\ = 178 \end{array}

We call this the Division Algorithm and will discuss it more formally after looking at an example.

Division of polynomials that contain more than one term has similarities to long division of whole numbers. We can write a polynomial dividend as the product of the divisor and the quotient added to the remainder. The terms of the polynomial division correspond to the digits (and place values) of the whole number division. This method allows us to divide two polynomials. For example, if we were to divide $2 x^{3} - 3 x^{2} + 4 x + 5$

by $x + 2$

using the long division algorithm, it would look like this:

Steps of long division for polynomials. We have found

\frac{2 x^{3} - 3 x^{2} + 4 x + 5}{x + 2} = 2 x^{2} - 7 x + 18 - \frac{31}{x + 2}

\frac{2 x^{3} - 3 x^{2} + 4 x + 5}{x + 2} = (x + 2) (2 x^{2} - 7 x + 18) - 31

We can identify the dividend, the divisor, the quotient, and the remainder.

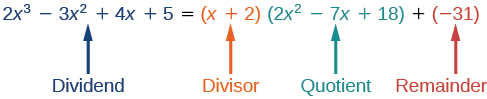Identifying the dividend, divisor, quotient and remainder of the polynomial 2x^3-3x^2+4x+5, which is the dividend. Writing the result in this manner illustrates the Division Algorithm.

The Division Algorithm

The Division Algorithm states that, given a polynomial dividend $f (x)$

and a non-zero polynomial divisor $d (x)$

where the degree of $d (x)$

is less than or equal to the degree of $f (x),$

there exist unique polynomials $q (x)$

and $r (x)$

such that

f (x) = d (x) q (x) + r (x)

q (x)

is the quotient and $r (x)$

is the remainder. The remainder is either equal to zero or has degree strictly less than $d (x) .$

If $r (x) = 0,$

then $d (x)$

divides evenly into $f (x) .$

This means that, in this case, both $d (x)$

and $q (x)$

are factors of $f (x) .$

Given a polynomial and a binomial, use long division to divide the polynomial by the binomial.

Set up the division problem.
Determine the first term of the quotient by dividing the leading term of the dividend by the leading term of the divisor.
Multiply the answer by the divisor and write it below the like terms of the dividend.
Subtract the bottom binomial from the top binomial.
Bring down the next term of the dividend.
Repeat steps 2–5 until reaching the last term of the dividend.
If the remainder is non-zero, express as a fraction using the divisor as the denominator.

Using Long Division to Divide a Second-Degree Polynomial

Divide $5 x^{2} + 3 x - 2$

by $x + 1.$

Steps of long division for polynomials. The quotient is $5 x - 2.$

The remainder is 0. We write the result as

\frac{5 x^{2} + 3 x - 2}{x + 1} = 5 x - 2

5 x^{2} + 3 x - 2 = (x + 1) (5 x - 2)

Analysis

This division problem had a remainder of 0. This tells us that the dividend is divided evenly by the divisor, and that the divisor is a factor of the dividend.

Using Long Division to Divide a Third-Degree Polynomial

Divide $6 x^{3} + 11 x^{2} - 31 x + 15$

by $3 x - 2.$

Steps of long division for polynomials. There is a remainder of 1. We can express the result as:

\frac{6 x^{3} + 11 x^{2} - 31 x + 15}{3 x - 2} = 2 x^{2} + 5 x - 7 + \frac{1}{3 x - 2}

Analysis

We can check our work by using the Division Algorithm to rewrite the solution. Then multiply.

(3 x - 2) (2 x^{2} + 5 x - 7) + 1 = 6 x^{3} + 11 x^{2} - 31 x + 15

Notice, as we write our result,

the dividend is $6 x^{3} + 11 x^{2} - 31 x + 15$
the divisor is $3 x - 2$
the quotient is $2 x^{2} + 5 x - 7$
the remainder is $1$

Divide $16 x^{3} - 12 x^{2} + 20 x - 3$

by $4 x + 5.$

4 x^{2} - 8 x + 15 - \frac{78}{4 x + 5}

Using Synthetic Division to Divide Polynomials

As we’ve seen, long division of polynomials can involve many steps and be quite cumbersome. Synthetic division is a shorthand method of dividing polynomials for the special case of dividing by a linear factor whose leading coefficient is 1.

To illustrate the process, recall the example at the beginning of the section.

Divide $2 x^{3} - 3 x^{2} + 4 x + 5$

by $x + 2$

using the long division algorithm.

The final form of the process looked like this:

There is a lot of repetition in the table. If we don’t write the variables but, instead, line up their coefficients in columns under the division sign and also eliminate the partial products, we already have a simpler version of the entire problem.

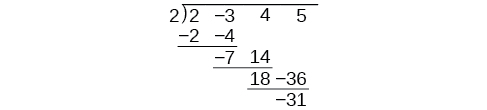Synthetic division of the polynomial 2x^3-3x^2+4x+5 by x+2 in which it only contains the coefficients of each polynomial. Synthetic division carries this simplification even a few more steps. Collapse the table by moving each of the rows up to fill any vacant spots. Also, instead of dividing by 2, as we would in division of whole numbers, then multiplying and subtracting the middle product, we change the sign of the “divisor” to –2, multiply and add. The process starts by bringing down the leading coefficient.

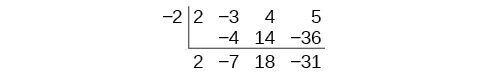Synthetic division of the polynomial 2x^3-3x^2+4x+5 by x+2 in which it only contains the coefficients of each polynomial. We then multiply it by the “divisor” and add, repeating this process column by column, until there are no entries left. The bottom row represents the coefficients of the quotient; the last entry of the bottom row is the remainder. In this case, the quotient is $2 x ² - 7 x + 18$

and the remainder is $–31.$

The process will be made more clear in [link].

Synthetic Division

Synthetic division is a shortcut that can be used when the divisor is a binomial in the form $x - k .$

In synthetic division, only the coefficients are used in the division process.

Given two polynomials, use synthetic division to divide.

Write $k$
for the divisor.
Write the coefficients of the dividend.
Bring the lead coefficient down.
Multiply the lead coefficient by $k .$
Write the product in the next column.
Add the terms of the second column.
Multiply the result by $k .$
Write the product in the next column.
Repeat steps 5 and 6 for the remaining columns.
Use the bottom numbers to write the quotient. The number in the last column is the remainder and has degree 0, the next number from the right has degree 1, the next number from the right has degree 2, and so on.

Using Synthetic Division to Divide a Second-Degree Polynomial

Use synthetic division to divide $5 x^{2} - 3 x - 36$

by $x - 3.$

Begin by setting up the synthetic division. Write $k$

and the coefficients.

A collapsed version of the previous synthetic division. Bring down the lead coefficient. Multiply the lead coefficient by $k .$

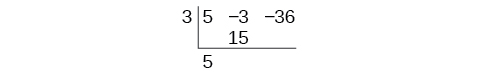$The set-up of the synthetic division for the polynomial 5x^2-3x-36 by x-3, which renders {5, -3, -36} by 3.$ Continue by adding the numbers in the second column. Multiply the resulting number by $k .$

Write the result in the next column. Then add the numbers in the third column.

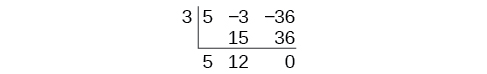Multiplied by the lead coefficient, 5, in the second column, and the lead coefficient is brought down to the second row. The result is $5 x + 12.$

The remainder is 0. So $x - 3$

is a factor of the original polynomial.

Analysis

Just as with long division, we can check our work by multiplying the quotient by the divisor and adding the remainder.

(x - 3) (5 x + 12) + 0 = 5 x^{2} - 3 x - 36

Using Synthetic Division to Divide a Third-Degree Polynomial

Use synthetic division to divide $4 x^{3} + 10 x^{2} - 6 x - 20$

by $x + 2.$

The binomial divisor is $x + 2$

so $k = - 2.$

Add each column, multiply the result by –2, and repeat until the last column is reached.

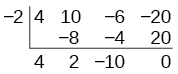Synthetic division of 4x^3+10x^2-6x-20 divided by x+2. The result is $4 x^{2} + 2 x - 10.$

The remainder is 0. Thus, $x + 2$

is a factor of $4 x^{3} + 10 x^{2} - 6 x - 20.$

Analysis

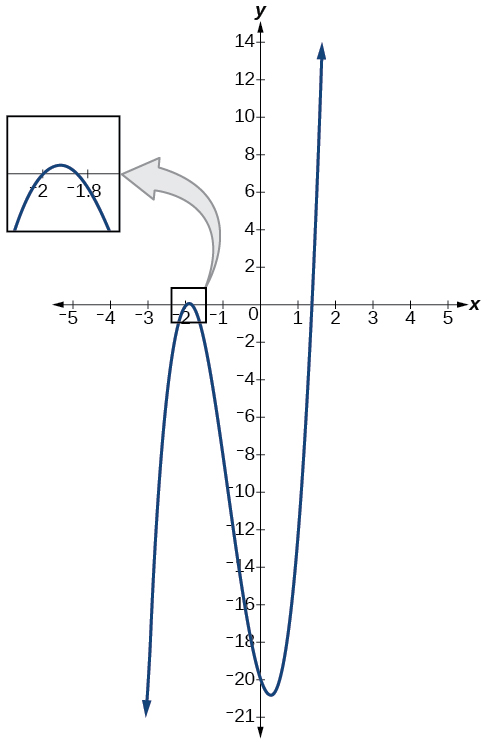
The graph of the polynomial function $f (x) = 4 x^{3} + 10 x^{2} - 6 x - 20$

in [link] shows a zero at $x = k = −2.$

This confirms that $x + 2$

is a factor of $4 x^{3} + 10 x^{2} - 6 x - 20.$

Synthetic division of 4x^3+10x^2-6x-20 divided by x+2.

Using Synthetic Division to Divide a Fourth-Degree Polynomial

Use synthetic division to divide $- 9 x^{4} + 10 x^{3} + 7 x^{2} - 6$

by $x - 1.$

Notice there is no x-term. We will use a zero as the coefficient for that term.* * *

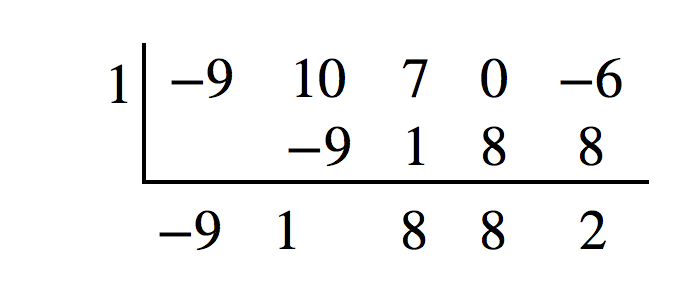The result is $- 9 x^{3} + x^{2} + 8 x + 8 + \frac{2}{x - 1} .$

Use synthetic division to divide $3 x^{4} + 18 x^{3} - 3 x + 40$

by $x + 7.$

3 x^{3} - 3 x^{2} + 21 x - 150 + \frac{1, 090}{x + 7}

Using Polynomial Division to Solve Application Problems

Polynomial division can be used to solve a variety of application problems involving expressions for area and volume. We looked at an application at the beginning of this section. Now we will solve that problem in the following example.

Using Polynomial Division in an Application Problem

The volume of a rectangular solid is given by the polynomial $3 x^{4} - 3 x^{3} - 33 x^{2} + 54 x .$

The length of the solid is given by $3 x$

and the width is given by $x - 2.$

Find the height of the solid.

There are a few ways to approach this problem. We need to divide the expression for the volume of the solid by the expressions for the length and width. Let us create a sketch as in [link].

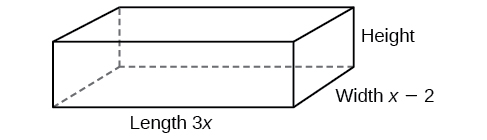
Graph of f(x)=4x^3+10x^2-6x-20 with a close up on x+2.

We can now write an equation by substituting the known values into the formula for the volume of a rectangular solid.

\begin{matrix} V = l \cdot w \cdot h \\ 3 x^{4} - 3 x^{3} - 33 x^{2} + 54 x = 3 x \cdot (x - 2) \cdot h \end{matrix}

To solve for $h,$

first divide both sides by $3 x .$

\begin{matrix} \frac{3 x \cdot (x - 2) \cdot h}{3 x} = \frac{3 x^{4} - 3 x^{3} - 33 x^{2} + 54 x}{3 x} \\ (x - 2) h = x^{3} - x^{2} - 11 x + 18 \end{matrix}

Now solve for $h$

using synthetic division.

h = \frac{x^{3} - x^{2} - 11 x + 18}{x - 2}

\begin{array}{l} 2 \begin{array}{r} 1 & - 1 & - 11 & 18 \\ 2 & 2 & - 18 \end{array} \\ \begin{array}{l} 1 & 1 & - 9 & 0 \end{array} \end{array}

The quotient is $x^{2} + x - 9$

and the remainder is 0. The height of the solid is $x^{2} + x - 9.$

The area of a rectangle is given by $3 x^{3} + 14 x^{2} - 23 x + 6.$

The width of the rectangle is given by $x + 6.$

Find an expression for the length of the rectangle.

3 x^{2} - 4 x + 1

Access these online resources for additional instruction and practice with polynomial division.

Key Equations

Division Algorithm

f (x) = d (x) q (x) + r (x)

where $q (x) \neq 0$

Key Concepts

Polynomial long division can be used to divide a polynomial by any polynomial with equal or lower degree. See [link] and [link].
The Division Algorithm tells us that a polynomial dividend can be written as the product of the divisor and the quotient added to the remainder.
Synthetic division is a shortcut that can be used to divide a polynomial by a binomial in the form $x - k .$
See [link], [link], and [link].
Polynomial division can be used to solve application problems, including area and volume. See [link].

Section Exercises

Verbal

If division of a polynomial by a binomial results in a remainder of zero, what can be conclude?

The binomial is a factor of the polynomial.

If a polynomial of degree $n$

is divided by a binomial of degree 1, what is the degree of the quotient?

Algebraic

For the following exercises, use long division to divide. Specify the quotient and the remainder.

(x^{2} + 5 x - 1) \div (x - 1)

x + 6 + \frac{5}{x - 1}, quotient: x + 6, remainder: 5

(2 x^{2} - 9 x - 5) \div (x - 5)

(3 x^{2} + 23 x + 14) \div (x + 7)

3 x + 2, quotient: 3 x + 2, remainder: 0

(4 x^{2} - 10 x + 6) \div (4 x + 2)

(6 x^{2} - 25 x - 25) \div (6 x + 5)

x - 5, quotient: x - 5, remainder: 0

(- x^{2} - 1) \div (x + 1)

(2 x^{2} - 3 x + 2) \div (x + 2)

2 x - 7 + \frac{16}{x + 2}, quotient: ​ 2 x - 7, remainder: 16

(x^{3} - 126) \div (x - 5)

(3 x^{2} - 5 x + 4) \div (3 x + 1)

x - 2 + \frac{6}{3 x + 1}, quotient: x - 2, remainder: 6

(x^{3} - 3 x^{2} + 5 x - 6) \div (x - 2)

(2 x^{3} + 3 x^{2} - 4 x + 15) \div (x + 3)

2 x^{2} - 3 x + 5, quotient: 2 x^{2} - 3 x + 5, remainder: 0

For the following exercises, use synthetic division to find the quotient.

(3 x^{3} - 2 x^{2} + x - 4) \div (x + 3)

(2 x^{3} - 6 x^{2} - 7 x + 6) \div (x - 4)

2 x^{2} + 2 x + 1 + \frac{10}{x - 4}

(6 x^{3} - 10 x^{2} - 7 x - 15) \div (x + 1)

(4 x^{3} - 12 x^{2} - 5 x - 1) \div (2 x + 1)

2 x^{2} - 7 x + 1 - \frac{2}{2 x + 1}

(9 x^{3} - 9 x^{2} + 18 x + 5) \div (3 x - 1)

(3 x^{3} - 2 x^{2} + x - 4) \div (x + 3)

3 x^{2} - 11 x + 34 - \frac{106}{x + 3}

(- 6 x^{3} + x^{2} - 4) \div (2 x - 3)

(2 x^{3} + 7 x^{2} - 13 x - 3) \div (2 x - 3)

x^{2} + 5 x + 1

(3 x^{3} - 5 x^{2} + 2 x + 3) \div (x + 2)

(4 x^{3} - 5 x^{2} + 13) \div (x + 4)

4 x^{2} - 21 x + 84 - \frac{323}{x + 4}

(x^{3} - 3 x + 2) \div (x + 2)

(x^{3} - 21 x^{2} + 147 x - 343) \div (x - 7)

x^{2} - 14 x + 49

(x^{3} - 15 x^{2} + 75 x - 125) \div (x - 5)

(9 x^{3} - x + 2) \div (3 x - 1)

3 x^{2} + x + \frac{2}{3 x - 1}

(6 x^{3} - x^{2} + 5 x + 2) \div (3 x + 1)

(x^{4} + x^{3} - 3 x^{2} - 2 x + 1) \div (x + 1)

x^{3} - 3 x + 1

(x^{4} - 3 x^{2} + 1) \div (x - 1)

(x^{4} + 2 x^{3} - 3 x^{2} + 2 x + 6) \div (x + 3)

x^{3} - x^{2} + 2

(x^{4} - 10 x^{3} + 37 x^{2} - 60 x + 36) \div (x - 2)

(x^{4} - 8 x^{3} + 24 x^{2} - 32 x + 16) \div (x - 2)

x^{3} - 6 x^{2} + 12 x - 8

(x^{4} + 5 x^{3} - 3 x^{2} - 13 x + 10) \div (x + 5)

(x^{4} - 12 x^{3} + 54 x^{2} - 108 x + 81) \div (x - 3)

x^{3} - 9 x^{2} + 27 x - 27

(4 x^{4} - 2 x^{3} - 4 x + 2) \div (2 x - 1)

(4 x^{4} + 2 x^{3} - 4 x^{2} + 2 x + 2) \div (2 x + 1)

2 x^{3} - 2 x + 2

For the following exercises, use synthetic division to determine whether the first expression is a factor of the second. If it is, indicate the factorization.

x - 2, 4 x^{3} - 3 x^{2} - 8 x + 4

x - 2, 3 x^{4} - 6 x^{3} - 5 x + 10

Yes $(x - 2) (3 x^{3} - 5)$

x + 3, - 4 x^{3} + 5 x^{2} + 8

x - 2, 4 x^{4} - 15 x^{2} - 4

Yes $(x - 2) (4 x^{3} + 8 x^{2} + x + 2)$

x - \frac{1}{2}, 2 x^{4} - x^{3} + 2 x - 1

x + \frac{1}{3}, 3 x^{4} + x^{3} - 3 x + 1

Graphical

For the following exercises, use the graph of the third-degree polynomial and one factor to write the factored form of the polynomial suggested by the graph. The leading coefficient is one.

Factor is $x^{2} - x + 3$

Graph of a polynomial that has a x-intercept at -1.

Factor is $(x^{2} + 2 x + 4)$

Graph of a polynomial that has a x-intercept at 1.

(x - 1) (x^{2} + 2 x + 4)

Factor is $x^{2} + 2 x + 5$

Graph of a polynomial that has a x-intercept at 2.

Factor is $x^{2} + x + 1$

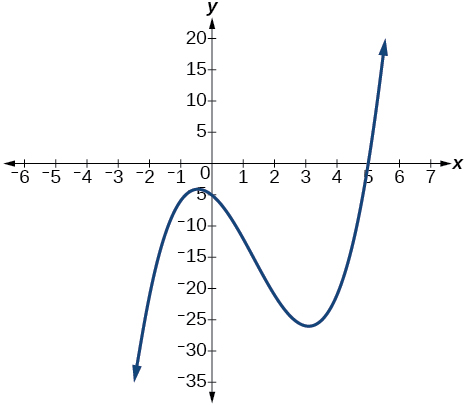
Graph of a polynomial that has a x-intercept at 5.

(x - 5) (x^{2} + x + 1)

Factor is $x^{2} + 2 x + 2$

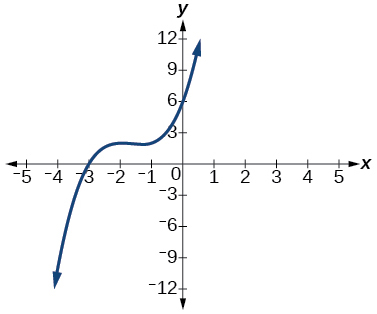
Graph of a polynomial that has a x-intercept at -3.

For the following exercises, use synthetic division to find the quotient and remainder.

\frac{4 x^{3} - 33}{x - 2}

Quotient: 4 x^{2} + 8 x + 16, remainder: - 1

\frac{2 x^{3} + 25}{x + 3}

\frac{3 x^{3} + 2 x - 5}{x - 1}

Quotient: 3 x^{2} + 3 x + 5, remainder: 0

\frac{- 4 x^{3} - x^{2} - 12}{x + 4}

\frac{x^{4} - 22}{x + 2}

Quotient: x^{3} - 2 x^{2} + 4 x - 8, remainder: - 6

Technology

For the following exercises, use a calculator with CAS to answer the questions.

Consider $\frac{x^{k} - 1}{x - 1}$

with $k = 1, 2, 3.$

What do you expect the result to be if $k = 4 ?$

Consider $\frac{x^{k} + 1}{x + 1}$

for $k = 1, 3, 5.$

What do you expect the result to be if $k = 7 ?$

x^{6} - x^{5} + x^{4} - x^{3} + x^{2} - x + 1

Consider $\frac{x^{4} - k^{4}}{x - k}$

for $k = 1, 2, 3.$

What do you expect the result to be if $k = 4 ?$

Consider $\frac{x^{k}}{x + 1}$

with $k = 1, 2, 3.$

What do you expect the result to be if $k = 4 ?$

x^{3} - x^{2} + x - 1 + \frac{1}{x + 1}

Consider $\frac{x^{k}}{x - 1}$

with $k = 1, 2, 3.$

What do you expect the result to be if $k = 4 ?$

Extensions

For the following exercises, use synthetic division to determine the quotient involving a complex number.

\frac{x + 1}{x - i}

1 + \frac{1 + i}{x - i}

\frac{x^{2} + 1}{x - i}

\frac{x + 1}{x + i}

1 + \frac{1 - i}{x + i}

\frac{x^{2} + 1}{x + i}

\frac{x^{3} + 1}{x - i}

x^{2} - i x - 1 + \frac{1 - i}{x - i}

Real-World Applications

For the following exercises, use the given length and area of a rectangle to express the width algebraically.

Length is $x + 5,$

area is $2 x^{2} + 9 x - 5.$

Length is $2 x + 5,$

area is $4 x^{3} + 10 x^{2} + 6 x + 15$

2 x^{2} + 3

Length is $3 x - 4,$

area is $6 x^{4} - 8 x^{3} + 9 x^{2} - 9 x - 4$

For the following exercises, use the given volume of a box and its length and width to express the height of the box algebraically.

Volume is $12 x^{3} + 20 x^{2} - 21 x - 36,$

length is $2 x + 3,$

width is $3 x - 4.$

2 x + 3

Volume is $18 x^{3} - 21 x^{2} - 40 x + 48,$

length is $3 x - 4,$

width is $3 x - 4.$

Volume is $10 x^{3} + 27 x^{2} + 2 x - 24,$

length is $5 x - 4,$

width is $2 x + 3.$

x + 2

Volume is $10 x^{3} + 30 x^{2} - 8 x - 24,$

length is $2,$

width is $x + 3.$

For the following exercises, use the given volume and radius of a cylinder to express the height of the cylinder algebraically.

Volume is $π (25 x^{3} - 65 x^{2} - 29 x - 3),$

radius is $5 x + 1.$

x - 3

Volume is $π (4 x^{3} + 12 x^{2} - 15 x - 50),$

radius is $2 x + 5.$

Volume is $π (3 x^{4} + 24 x^{3} + 46 x^{2} - 16 x - 32),$

radius is $x + 4.$

3 x^{2} - 2

Footnotes

1 National Park Service. "Lincoln Memorial Building Statistics." http://www.nps.gov/linc/historyculture/lincoln-memorial-building-statistics.htm. Accessed 4/3/2014

Glossary

Division Algorithm

given a polynomial dividend

f (x)

and a non-zero polynomial divisor

d (x)

where the degree of

d (x)

is less than or equal to the degree of

f (x),

there exist unique polynomials

q (x)

and

r (x)

such that

f (x) = d (x) q (x) + r (x)

where

q (x)

is the quotient and

r (x)

is the remainder. The remainder is either equal to zero or has degree strictly less than

d (x) .

synthetic division: a shortcut method that can be used to divide a polynomial by a binomial of the form $x - k$

This work is licensed under a Creative Commons Attribution 4.0 International License.

You can also download for free at http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@8.1

Attribution:

For questions regarding this license, please contact partners@openstaxcollege.org.
If you use this textbook as a bibliographic reference, then you should cite it as follows: OpenStax College, Precalculus. OpenStax CNX. http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@8.1.
If you redistribute this textbook in a print format, then you must include on every physical page the following attribution: "Download for free at http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@8.1."
If you redistribute part of this textbook, then you must retain in every digital format page view (including but not limited to EPUB, PDF, and HTML) and on every physical printed page the following attribution: "Download for free at http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@8.1."