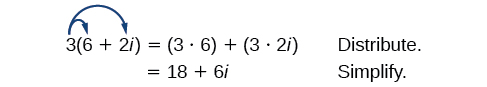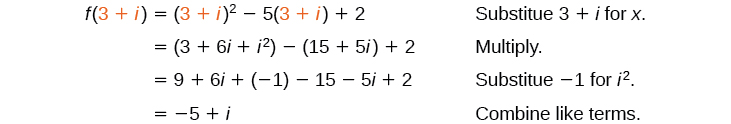Complex Numbers
In this section, you will:
- Express square roots of negative numbers as multiples of
.
- Plot complex numbers on the complex plane.
- Add and subtract complex numbers.
- Multiply and divide complex numbers.
The study of mathematics continuously builds upon itself. Negative integers, for example, fill a void left by the set of positive integers. The set of rational numbers, in turn, fills a void left by the set of integers. The set of real numbers fills a void left by the set of rational numbers. Not surprisingly, the set of real numbers has voids as well. For example, we still have no solution to equations such as
Our best guesses might be +2 or –2. But if we test +2 in this equation, it does not work. If we test –2, it does not work. If we want to have a solution for this equation, we will have to go farther than we have so far. After all, to this point we have described the square root of a negative number as undefined. Fortunately, there is another system of numbers that provides solutions to problems such as these. In this section, we will explore this number system and how to work within it.
Expressing Square Roots of Negative Numbers as Multiples of i
We know how to find the square root of any positive real number. In a similar way, we can find the square root of a negative number. The difference is that the root is not real. If the value in the radicand is negative, the root is said to be an imaginary number. The imaginary number
is defined as the square root of negative 1.
So, using properties of radicals,
We can write the square root of any negative number as a multiple of
Consider the square root of –25.
We use
and not
because the principal root of
is the positive root.
A complex number is the sum of a real number and an imaginary number. A complex number is expressed in standard form when written
where
is the real part and
is the imaginary part. For example,
is a complex number. So, too, is
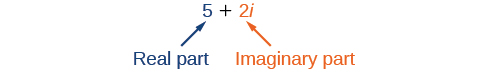 Imaginary numbers are distinguished from real numbers because a squared imaginary number produces a negative real number. Recall, when a positive real number is squared, the result is a positive real number and when a negative real number is squared, again, the result is a positive real number. Complex numbers are a combination of real and imaginary numbers.
Imaginary numbers are distinguished from real numbers because a squared imaginary number produces a negative real number. Recall, when a positive real number is squared, the result is a positive real number and when a negative real number is squared, again, the result is a positive real number. Complex numbers are a combination of real and imaginary numbers.
Imaginary and Complex Numbers
A complex number is a number of the form
where
If
then
is a real number. If
and
is not equal to 0, the complex number is called an imaginary number. An imaginary number is an even root of a negative number.
Given an imaginary number, express it in standard form.
- Write
as
- Express
as
- Write
in simplest form.
Expressing an Imaginary Number in Standard Form
Express
in standard form.
In standard form, this is
Express
in standard form.
Plotting a Complex Number on the Complex Plane
We cannot plot complex numbers on a number line as we might real numbers. However, we can still represent them graphically. To represent a complex number we need to address the two components of the number. We use the complex plane, which is a coordinate system in which the horizontal axis represents the real component and the vertical axis represents the imaginary component. Complex numbers are the points on the plane, expressed as ordered pairs
where
represents the coordinate for the horizontal axis and
represents the coordinate for the vertical axis.
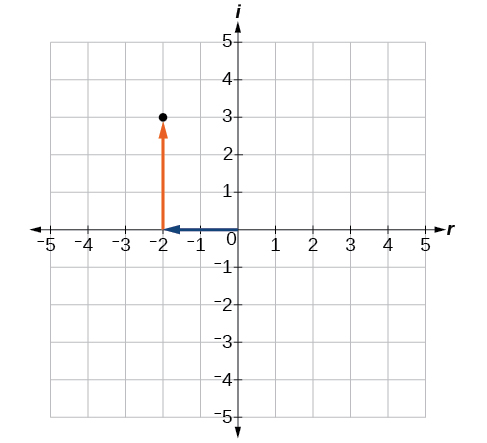
Let’s consider the number
The real part of the complex number is
and the imaginary part is
We plot the ordered pair
to represent the complex number
as shown in [link].
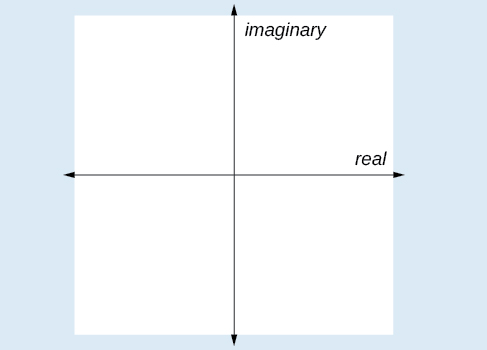
Complex Plane
In the complex plane, the horizontal axis is the real axis, and the vertical axis is the imaginary axis as shown in [link].
Given a complex number, represent its components on the complex plane.
- Determine the real part and the imaginary part of the complex number.
- Move along the horizontal axis to show the real part of the number.
- Move parallel to the vertical axis to show the imaginary part of the number.
- Plot the point.
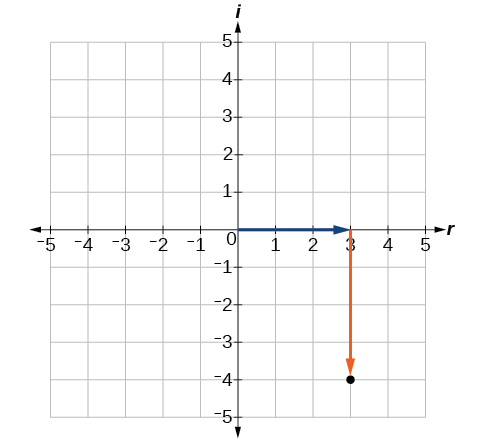
Plotting a Complex Number on the Complex Plane
Plot the complex number
on the complex plane.
The real part of the complex number is
and the imaginary part is
We plot the ordered pair
as shown in [link].
Plot the complex number
on the complex plane.

Adding and Subtracting Complex Numbers
Just as with real numbers, we can perform arithmetic operations on complex numbers. To add or subtract complex numbers, we combine the real parts and combine the imaginary parts.
Complex Numbers: Addition and Subtraction
Adding complex numbers:
Subtracting complex numbers:
Given two complex numbers, find the sum or difference.
- Identify the real and imaginary parts of each number.
- Add or subtract the real parts.
- Add or subtract the imaginary parts.
Adding Complex Numbers
Add
and
We add the real parts and add the imaginary parts.
Multiplying Complex Numbers
Multiplying complex numbers is much like multiplying binomials. The major difference is that we work with the real and imaginary parts separately.
Multiplying a Complex Numbers by a Real Number
Let’s begin by multiplying a complex number by a real number. We distribute the real number just as we would with a binomial. So, for example,
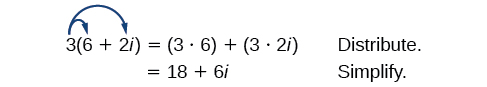 <div data-type="note" data-has-label="true" class="precalculus howto" data-label="How To Feature" markdown="1">
Given a complex number and a real number, multiply to find the product.
<div data-type="note" data-has-label="true" class="precalculus howto" data-label="How To Feature" markdown="1">
Given a complex number and a real number, multiply to find the product.
- Use the distributive property.
- Simplify.
</div>
Multiplying a Complex Number by a Real Number
Find the product
Distribute the 4.
Find the product
Multiplying Complex Numbers Together
Now, let’s multiply two complex numbers. We can use either the distributive property or the FOIL method. Recall that FOIL is an acronym for multiplying First, Outer, Inner, and Last terms together. Using either the distributive property or the FOIL method, we get
Because
we have
To simplify, we combine the real parts, and we combine the imaginary parts.
Given two complex numbers, multiply to find the product.
- Use the distributive property or the FOIL method.
- Simplify.
Multiplying a Complex Number by a Complex Number
Multiply
Use
Dividing Complex Numbers
Division of two complex numbers is more complicated than addition, subtraction, and multiplication because we cannot divide by an imaginary number, meaning that any fraction must have a real-number denominator. We need to find a term by which we can multiply the numerator and the denominator that will eliminate the imaginary portion of the denominator so that we end up with a real number as the denominator. This term is called the complex conjugate of the denominator, which is found by changing the sign of the imaginary part of the complex number. In other words, the complex conjugate of
is
Note that complex conjugates have a reciprocal relationship: The complex conjugate of
is
and the complex conjugate of
is
Further, when a quadratic equation with real coefficients has complex solutions, the solutions are always complex conjugates of one another.
Suppose we want to divide
by
where neither
nor
equals zero. We first write the division as a fraction, then find the complex conjugate of the denominator, and multiply.
Multiply the numerator and denominator by the complex conjugate of the denominator.
Apply the distributive property.
Simplify, remembering that
The Complex Conjugate
The complex conjugate of a complex number
is
It is found by changing the sign of the imaginary part of the complex number. The real part of the number is left unchanged.
- When a complex number is multiplied by its complex conjugate, the result is a real number.
- When a complex number is added to its complex conjugate, the result is a real number.
Finding Complex Conjugates
Find the complex conjugate of each number.
-
-
- The number is already in the form
The complex conjugate is
or
- We can rewrite this number in the form
as
The complex conjugate is
or
This can be written simply as
Analysis
Although we have seen that we can find the complex conjugate of an imaginary number, in practice we generally find the complex conjugates of only complex numbers with both a real and an imaginary component. To obtain a real number from an imaginary number, we can simply multiply by
Given two complex numbers, divide one by the other.
- Write the division problem as a fraction.
- Determine the complex conjugate of the denominator.
- Multiply the numerator and denominator of the fraction by the complex conjugate of the denominator.
- Simplify.
Dividing Complex Numbers
Divide
by
We begin by writing the problem as a fraction.
Then we multiply the numerator and denominator by the complex conjugate of the denominator.
To multiply two complex numbers, we expand the product as we would with polynomials (the process commonly called FOIL).
Note that this expresses the quotient in standard form.
Substituting a Complex Number into a Polynomial Function
Let
Evaluate
Substitute
into the function
and simplify.
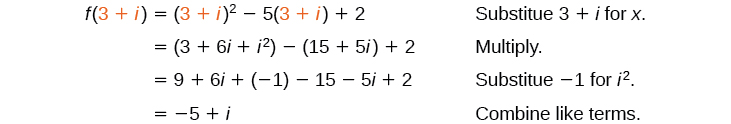
Analysis
We write
Notice that the input is
and the output is
Let
Evaluate
Substituting an Imaginary Number in a Rational Function
Let
Evaluate
Substitute
and simplify.
Let
Evaluate
Simplifying Powers of i
The powers of
are cyclic. Let’s look at what happens when we raise
to increasing powers.
We can see that when we get to the fifth power of
it is equal to the first power. As we continue to multiply
by itself for increasing powers, we will see a cycle of 4. Let’s examine the next 4 powers of
Simplifying Powers of
Evaluate
Since
we can simplify the problem by factoring out as many factors of
as possible. To do so, first determine how many times 4 goes into 35:
**Can we write
in other helpful ways?**
*As we saw in [link], we reduced
to
by dividing the exponent by 4 and using the remainder to find the simplified form. But perhaps another factorization of
may be more useful. [link] shows some other possible factorizations.*
| Factorization of
i
35
</math></strong> |
| |
|
| Reduced form |
|
| |
|
| Simplified form |
|
Each of these will eventually result in the answer we obtained above but may require several more steps than our earlier method.
Key Concepts
Verbal
Explain how to add complex numbers.
Add the real parts together and the imaginary parts together.
What is the basic principle in multiplication of complex numbers?
Give an example to show the product of two imaginary numbers is not always imaginary.
times
equals –1, which is not imaginary. (answers vary)
What is a characteristic of the plot of a real number in the complex plane?
Algebraic
For the following exercises, evaluate the algebraic expressions.
evaluate
evaluate
evaluate
evaluate
evaluate
evaluate
Graphical
For the following exercises, determine the number of real and nonreal solutions for each quadratic function shown.


For the following exercises, plot the complex numbers on the complex plane.


Numeric
For the following exercises, perform the indicated operation and express the result as a simplified complex number.
Technology
For the following exercises, use a calculator to help answer the questions.
Evaluate
for
Predict the value if
Evaluate
for
Predict the value if
Evaluate
for
. Predict the value for
Show that a solution of
is
Show that a solution of
is
Extensions
For the following exercises, evaluate the expressions, writing the result as a simplified complex number.
Glossary
- complex conjugate
- the complex number in which the sign of the imaginary part is changed and the real part of the number is left unchanged; when added to or multiplied by the original complex number, the result is a real number
- complex number
- the sum of a real number and an imaginary number, written in the standard form
where
is the real part, and
is the imaginary part
- complex plane
- a coordinate system in which the horizontal axis is used to represent the real part of a complex number and the vertical axis is used to represent the imaginary part of a complex number
- imaginary number
- a number in the form
where

This work is licensed under a Creative Commons Attribution 4.0 International License.
You can also download for free at http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@8.1
Attribution:
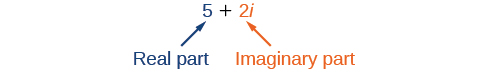 Imaginary numbers are distinguished from real numbers because a squared imaginary number produces a negative real number. Recall, when a positive real number is squared, the result is a positive real number and when a negative real number is squared, again, the result is a positive real number. Complex numbers are a combination of real and imaginary numbers.
Imaginary numbers are distinguished from real numbers because a squared imaginary number produces a negative real number. Recall, when a positive real number is squared, the result is a positive real number and when a negative real number is squared, again, the result is a positive real number. Complex numbers are a combination of real and imaginary numbers.