Huygens's Principle: Diffraction

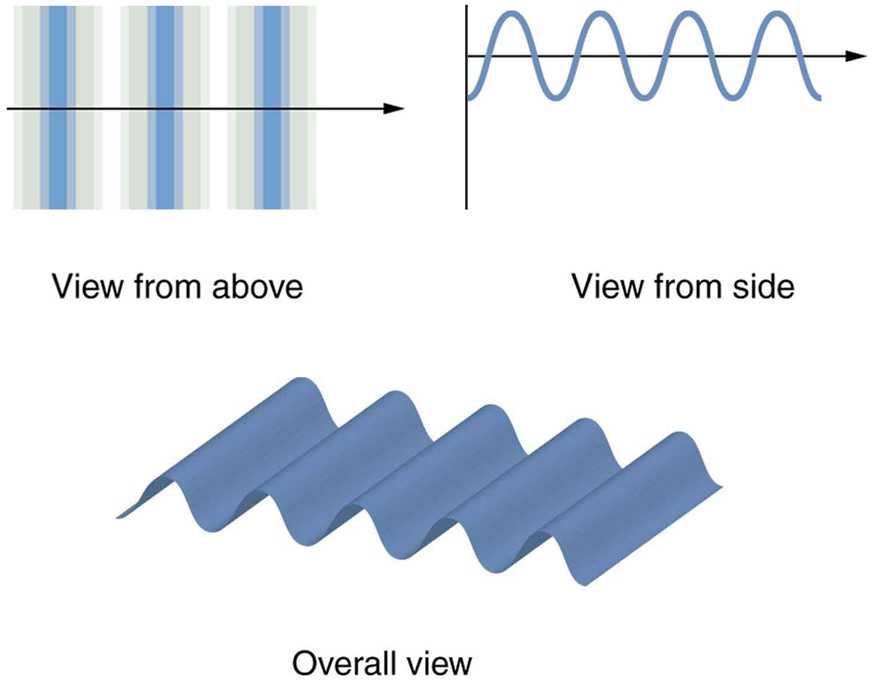
[link] shows how a transverse wave looks as viewed from above and from the side. A light wave can be imagined to propagate like this, although we do not actually see it wiggling through space. From above, we view the wavefronts (or wave crests) as we would by looking down on the ocean waves. The side view would be a graph of the electric or magnetic field. The view from above is perhaps the most useful in developing concepts about wave optics.

The figure contains three images. The first image, labeled view from above, represents a wave viewed from above as a series of thin, straight strips arranged adjacent to each other across the page. The color of the strips changes gradually from a darker blue near the crests of the waves to white near the troughs of the waves. A single black horizontal arrow points from left to right across the image. The second image, labeled view from side, shows a typical sine curve oscillating above and below a black arrow pointing to the right that serves as the horizontal axis. The sine wave has the same wavelength as the wave viewed from above. The third image, labeled overall view, is a perspective view of a wave of the same wavelength as in the first two images.

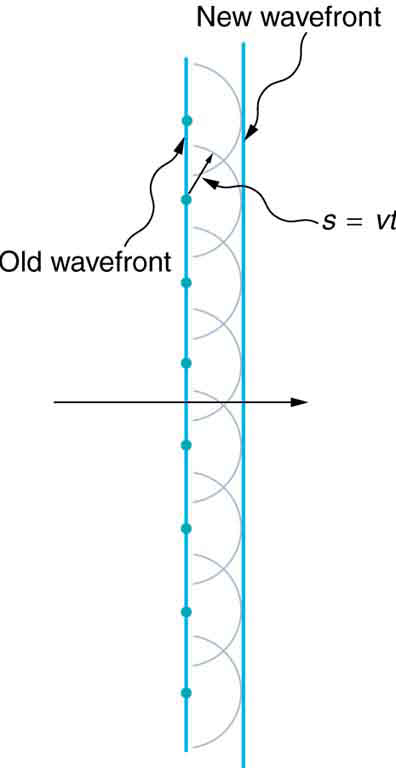
The Dutch scientist Christiaan Huygens (1629–1695) developed a useful technique for determining in detail how and where waves propagate. Starting from some known position, Huygens’s principle states that:

Every point on a wavefront is a source of wavelets that spread out in the forward direction at the same speed as the wave itself. The new wavefront is a line tangent to all of the wavelets.

[link] shows how Huygens’s principle is applied. A wavefront is the long edge that moves, for example, the crest or the trough. Each point on the wavefront emits a semicircular wave that moves at the propagation speed v size 12{v} {}

. These are drawn at a time t size 12{t} {}

later, so that they have moved a distance s=vt size 12{s= ital "vt"} {}

. The new wavefront is a line tangent to the wavelets and is where we would expect the wave to be a time t size 12{t} {}

later. Huygens’s principle works for all types of waves, including water waves, sound waves, and light waves. We will find it useful not only in describing how light waves propagate, but also in explaining the laws of reflection and refraction. In addition, we will see that Huygens’s principle tells us how and where light rays interfere.

This figure shows two straight vertical lines, with the left line labeled old wavefront and the right line labeled new wavefront. In the center of the image, a horizontal black arrow crosses both lines and points to the right. The old wavefront line passes through eight evenly spaced dots, with four dots above the black arrow and four dots below the black arrow. Each dot serves as the center of a corresponding semicircle, and all eight semicircles are the same size. The point on each semicircle that is on the same horizontal level as the corresponding center dot touches the new wavefront line, as if the semicircles are pushing the new wavefront line away from the old wavefront line. One of the center dots has a radial arrow pointing to a point on the corresponding semicircle. This radial arrow is labeled s equals v t.

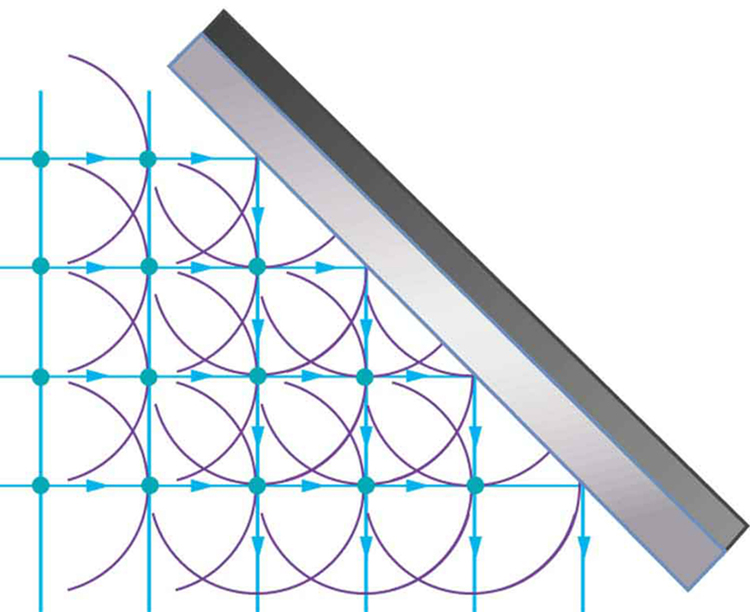
[link] shows how a mirror reflects an incoming wave at an angle equal to the incident angle, verifying the law of reflection. As the wavefront strikes the mirror, wavelets are first emitted from the left part of the mirror and then the right. The wavelets closer to the left have had time to travel farther, producing a wavefront traveling in the direction shown.

The figure shows a grid pattern made of dots. The overall grid pattern would be square were its upper-right four dots not cut off by a gray solid rectangle oriented at forty five degrees counterclockwise from the vertical. Semicircles representing wavelets are centered on each dot. Arrows indicate that the wavelets approach the angled surface from the left and then reflect downward.

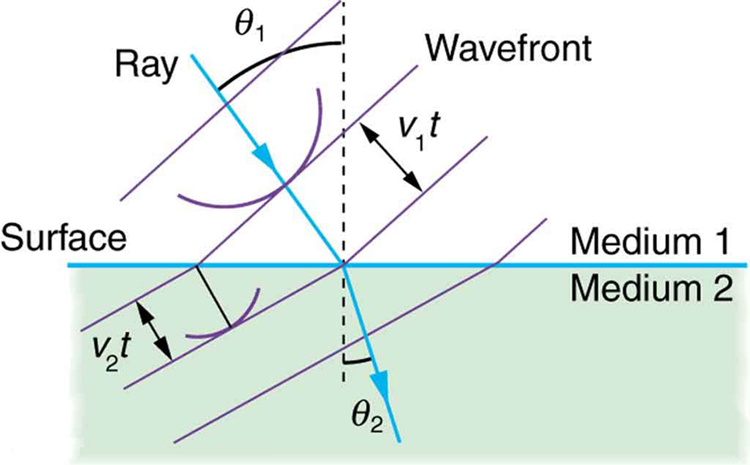
The law of refraction can be explained by applying Huygens’s principle to a wavefront passing from one medium to another (see [link]). Each wavelet in the figure was emitted when the wavefront crossed the interface between the media. Since the speed of light is smaller in the second medium, the waves do not travel as far in a given time, and the new wavefront changes direction as shown. This explains why a ray changes direction to become closer to the perpendicular when light slows down. Snell’s law can be derived from the geometry in [link], but this is left as an exercise for ambitious readers.

The figure shows two media separated by a horizontal line labeled surface. The upper medium is labeled medium one and the lower medium is labeled medium two. A vertical dotted line cuts through both media and is perpendicular to the surface. The point where the dotted line crosses the surface between the media will be called the point of contact. In medium one, a ray pointing down and to the right makes an abrupt turn at the point of contact. The path of the ray makes an angle theta sub one with the dotted line in medium one. In medium two, the ray leaves the point of contact and follows a path that makes an angle theta sub two with the dotted line in medium two, where theta sub two is less than theta sub one. We will call these the incident ray and the refracted ray, respectively. Thus, the refracted ray is closer to being vertical than the incident ray. Three line segments, labeled wavefront, are drawn perpendicular to the incident ray and the refracted ray. These line segments are equally spaced for both rays, but the three line segments that cross the incident ray are shorter and more widely spaced than the three line segments that cross the refracted ray. The separation of these line segments is labeled v sub one t for the incident ray and v sub two t for the refracted ray, with v sub two t being less than v sub one t.

What happens when a wave passes through an opening, such as light shining through an open door into a dark room? For light, we expect to see a sharp shadow of the doorway on the floor of the room, and we expect no light to bend around corners into other parts of the room. When sound passes through a door, we expect to hear it everywhere in the room and, thus, expect that sound spreads out when passing through such an opening (see [link]). What is the difference between the behavior of sound waves and light waves in this case? The answer is that light has very short wavelengths and acts like a ray. Sound has wavelengths on the order of the size of the door and bends around corners (for frequency of 1000 Hz, λ=c/f=(330m/s)/(1000s−1)=0.33 m size 12{λ=c/f= \( "330"`m/s \) / \( "1000"`s rSup { size 8{ - 1} } \) =0 "." "33"`m} {}

, about three times smaller than the width of the doorway).

Part a of the figure is a view from above of a diagram of a wall in which is cut an open door. The wall extends from the bottom of the diagram to the top, and the door forms a gap in the wall. The door itself is opened to the left and is positioned about forty five degrees from the wall on which it pivots. From the left comes a bright light, which is labeled small lambda, and the door and wall create sharp shadows by blocking this light. The edges of these shadows are labeled straight-edge shadows. Some of the light passes through the open doorway. Part b of the figure shows a similar diagram. A line parallel to the wall approaches the wall from the left and is labeled plane wavefront of sound. There are five dots evenly spaced across the open doorway, labeled one through five. Semicircles appear to the right of these dots entering the room to the right of the wall. Bracketing all these semicircles is a line that has the form of closing square bracket with rounded corners. This line is labeled sound. There are five rays shown pointing from the bracketing line into the room to the right of the wall. Three of these rays point horizontally to the right, one ray points upward and to the right, and the last ray points downward and to the right. This last ray points to the ear of a person who we see from above and who is labeled listener. The diagram indicates that the listener hears sound around the corner of the door.

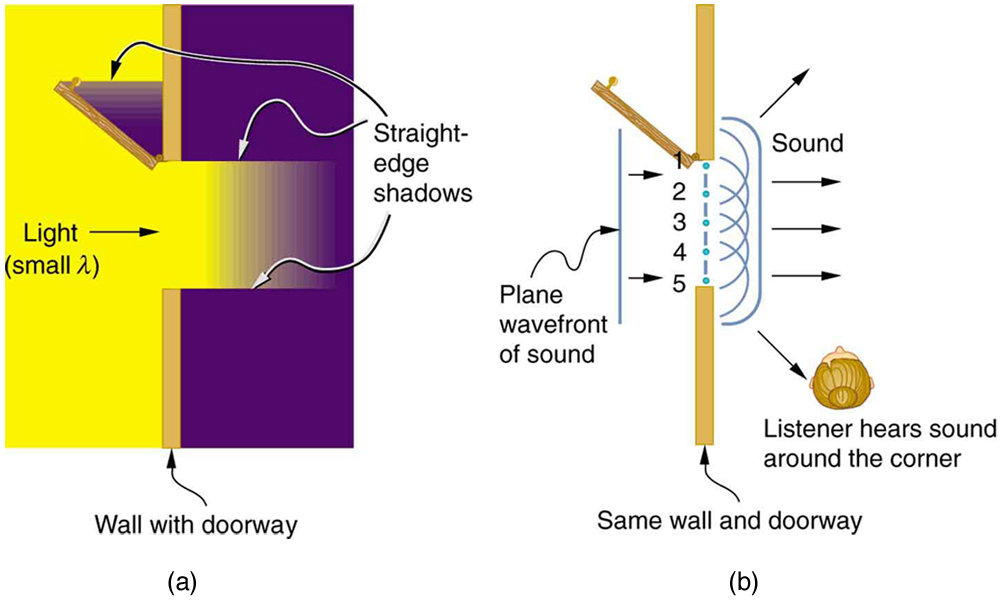
If we pass light through smaller openings, often called slits, we can use Huygens’s principle to see that light bends as sound does (see [link]). The bending of a wave around the edges of an opening or an obstacle is called diffraction. Diffraction is a wave characteristic and occurs for all types of waves. If diffraction is observed for some phenomenon, it is evidence that the phenomenon is a wave. Thus the horizontal diffraction of the laser beam after it passes through slits in [link] is evidence that light is a wave.

Three related diagrams showing how waves spread out when passing through various-size openings. The first diagram shows wavefronts passing through an opening that is wide compared to the distance between successive wavefronts. The wavefronts that emerge on the other side of the opening have minor bending along the edges. The second diagram shows wavefronts passing through a smaller opening. The waves experience more bending. The third diagram shows wavefronts passing through an opening that has a size similar to the spacing between wavefronts. These waves show significant bending.

Section Summary

Conceptual Questions

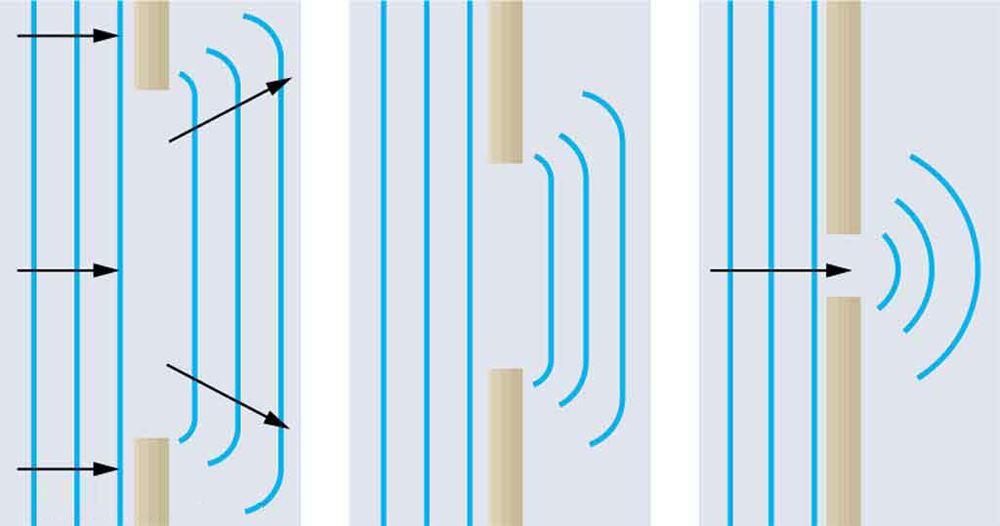
How do wave effects depend on the size of the object with which the wave interacts? For example, why does sound bend around the corner of a building while light does not?

Under what conditions can light be modeled like a ray? Like a wave?

Go outside in the sunlight and observe your shadow. It has fuzzy edges even if you do not. Is this a diffraction effect? Explain.

Why does the wavelength of light decrease when it passes from vacuum into a medium? State which attributes change and which stay the same and, thus, require the wavelength to decrease.

Does Huygens’s principle apply to all types of waves?

Glossary

diffraction
the bending of a wave around the edges of an opening or an obstacle
Huygens’s principle
every point on a wavefront is a source of wavelets that spread out in the forward direction at the same speed as the wave itself. The new wavefront is a line tangent to all of the wavelets
Creative Commons License
This work is licensed under a Creative Commons Attribution 4.0 International License.

You can also download for free at http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@11.1

Attribution: