Null Measurements

Standard measurements of voltage and current alter the circuit being measured, introducing uncertainties in the measurements. Voltmeters draw some extra current, whereas ammeters reduce current flow. Null measurements balance voltages so that there is no current flowing through the measuring device and, therefore, no alteration of the circuit being measured.

Null measurements are generally more accurate but are also more complex than the use of standard voltmeters and ammeters, and they still have limits to their precision. In this module, we shall consider a few specific types of null measurements, because they are common and interesting, and they further illuminate principles of electric circuits.

The Potentiometer

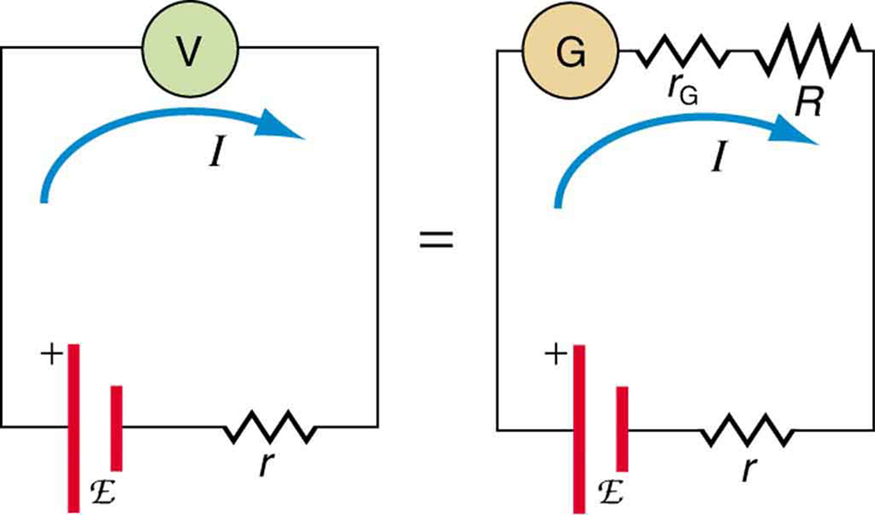
Suppose you wish to measure the emf of a battery. Consider what happens if you connect the battery directly to a standard voltmeter as shown in [link]. (Once we note the problems with this measurement, we will examine a null measurement that improves accuracy.) As discussed before, the actual quantity measured is the terminal voltage V size 12{V} {}

, which is related to the emf of the battery by V=emf−Ir size 12{V="emf" - ital "Ir"} {}

, where I size 12{I} {}

is the current that flows and r size 12{r} {}

is the internal resistance of the battery.

The emf could be accurately calculated if r size 12{r} {}

were very accurately known, but it is usually not. If the current I size 12{I} {}

could be made zero, then V=emf size 12{V="emf"} {}

, and so emf could be directly measured. However, standard voltmeters need a current to operate; thus, another technique is needed.

The diagram shows equivalence between two circuits. The first circuit has a cell of e m f script E and an internal resistance r connected across a voltmeter. The equivalent circuit on the right shows the same cell of e m f script E and an internal resistance r connected across a series combination of a galvanometer with an internal resistance r sub G and high resistance R. The currents in the two circuits are shown to be equal.

A potentiometer is a null measurement device for measuring potentials (voltages). (See [link].) A voltage source is connected to a resistor R,

say, a long wire, and passes a constant current through it. There is a steady drop in potential (an IR size 12{ ital "IR"} {}

drop) along the wire, so that a variable potential can be obtained by making contact at varying locations along the wire.

[link](b) shows an unknown emfx size 12{"emf" rSub { size 8{x} } } {}

(represented by script Ex size 12{"emf" rSub { size 8{x} } } {}

in the figure) connected in series with a galvanometer. Note that emfx size 12{"emf" rSub { size 8{x} } } {}

opposes the other voltage source. The location of the contact point (see the arrow on the drawing) is adjusted until the galvanometer reads zero. When the galvanometer reads zero, emfx=IRx size 12{"emf" rSub { size 8{x} } = ital "IR" rSub { size 8{x} } } {}

, where Rx size 12{R rSub { size 8{x} } } {}

is the resistance of the section of wire up to the contact point. Since no current flows through the galvanometer, none flows through the unknown emf, and so emfx size 12{"emf" rSub { size 8{x} } } {}

is directly sensed.

Now, a very precisely known standard emfs size 12{"emf" rSub { size 8{s} } } {}

is substituted for emfx size 12{"emf" rSub { size 8{x} } } {}

, and the contact point is adjusted until the galvanometer again reads zero, so that emfs=IRs size 12{"emf" rSub { size 8{s} } = ital "IR" rSub { size 8{s} } } {}

. In both cases, no current passes through the galvanometer, and so the current I size 12{I} {}

through the long wire is the same. Upon taking the ratio emfxemfs size 12{ { {"emf" rSub { size 8{x} } } over {"emf" rSub { size 8{s} } } } } {}

, I size 12{I} {}

cancels, giving

emfxemfs=IRxIRs=RxRs. size 12{ { {"emf" rSub { size 8{x} } } over {"emf" rSub { size 8{s} } } } = { { ital "IR" rSub { size 8{x} } } over { ital "IR" rSub { size 8{s} } } } = { {R rSub { size 8{x} } } over {R rSub { size 8{s} } } } } {}

Solving for emfx size 12{"emf" rSub { size 8{x} } } {}

gives

emfx=emfsRxRs. size 12{"emf" rSub { size 8{x} } ="emf" rSub { size 8{s} } { {R rSub { size 8{x} } } over {R rSub { size 8{s} } } } } {}

Two circuits are shown. The first circuit has a cell of e m f script E and internal resistance r connected in series to a resistor R. The second diagram shows the same circuit with the addition of a galvanometer and unknown voltage source connected with a variable contact that can be adjusted up and down the length of the resistor R.

Because a long uniform wire is used for R size 12{R} {}

, the ratio of resistances Rx/Rs size 12{R rSub { size 8{x} } /R rSub { size 8{s} } } {}

is the same as the ratio of the lengths of wire that zero the galvanometer for each emf. The three quantities on the right-hand side of the equation are now known or measured, and emfx size 12{"emf" rSub { size 8{x} } } {}

can be calculated. The uncertainty in this calculation can be considerably smaller than when using a voltmeter directly, but it is not zero. There is always some uncertainty in the ratio of resistances Rx/Rs size 12{R rSub { size 8{x} } /R rSub { size 8{s} } } {}

and in the standard emfs size 12{"emf" rSub { size 8{s} } } {}

. Furthermore, it is not possible to tell when the galvanometer reads exactly zero, which introduces error into both Rx size 12{R rSub { size 8{x} } } {}

and Rs size 12{R rSub { size 8{s} } } {}

, and may also affect the current I size 12{I} {}

.

Resistance Measurements and the Wheatstone Bridge

There is a variety of so-called ohmmeters that purport to measure resistance. What the most common ohmmeters actually do is to apply a voltage to a resistance, measure the current, and calculate the resistance using Ohm’s law. Their readout is this calculated resistance. Two configurations for ohmmeters using standard voltmeters and ammeters are shown in [link]. Such configurations are limited in accuracy, because the meters alter both the voltage applied to the resistor and the current that flows through it.

The diagram shows two circuits. The first one has a cell of e m f script E and internal resistance r connected in series to an ammeter A and a resistor R. The second circuit is the same as the first, but in addition there is a voltmeter connected across the voltage source E.

The Wheatstone bridge is a null measurement device for calculating resistance by balancing potential drops in a circuit. (See [link].) The device is called a bridge because the galvanometer forms a bridge between two branches. A variety of bridge devices are used to make null measurements in circuits.

Resistors R1 size 12{R rSub { size 8{1} } } {}

and R2 size 12{R rSub { size 8{2} } } {}

are precisely known, while the arrow through R3 size 12{R rSub { size 8{3} } } {}

indicates that it is a variable resistance. The value of R3 size 12{R rSub { size 8{3} } } {}

can be precisely read. With the unknown resistance Rx size 12{R rSub { size 8{x} } } {}

in the circuit, R3 size 12{R rSub { size 8{3} } } {}

is adjusted until the galvanometer reads zero. The potential difference between points b and d is then zero, meaning that b and d are at the same potential. With no current running through the galvanometer, it has no effect on the rest of the circuit. So the branches abc and adc are in parallel, and each branch has the full voltage of the source. That is, the IR size 12{ ital "IR"} {}

drops along abc and adc are the same. Since b and d are at the same potential, the IR size 12{ ital "IR"} {}

drop along ad must equal the IR size 12{ ital "IR"} {}

drop along ab. Thus,

I1R1=I2R3. size 12{I rSub { size 8{1} } R rSub { size 8{1} } =I rSub { size 8{2} } R rSub { size 8{3} } } {}

Again, since b and d are at the same potential, the IR size 12{ ital "IR"} {}

drop along dc must equal the IR size 12{ ital "IR"} {}

drop along bc. Thus,

I1R2=I2Rx. size 12{I rSub { size 8{1} } R rSub { size 8{2} } =I rSub { size 8{2} } R rSub { size 8{x} } } {}

Taking the ratio of these last two expressions gives

I1R1I1R2=I2R3I2Rx. size 12{ { {I rSub { size 8{1} } R rSub { size 8{1} } } over {I rSub { size 8{1} } R rSub { size 8{2} } } } = { {I rSub { size 8{2} } R rSub { size 8{3} } } over {I rSub { size 8{2} } R rSub { size 8{x} } } } } {}

Canceling the currents and solving for Rx yields

Rx=R3R2R1. size 12{R rSub { size 8{x} } =R rSub { size 8{3} } { {R rSub { size 8{2} } } over {R rSub { size 8{1} } } } } {}

This complex circuit diagram shows a galvanometer connected in the center arm of a Wheatstone bridge arrangement. All the other four arms have a resistor. The bridge is connected to a cell of e m f script E and internal resistance r.

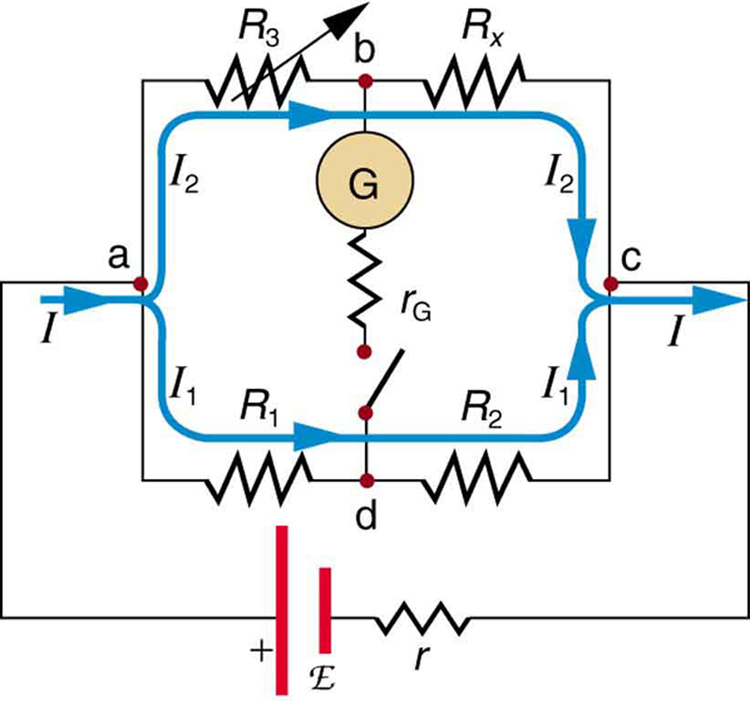
This equation is used to calculate the unknown resistance when current through the galvanometer is zero. This method can be very accurate (often to four significant digits), but it is limited by two factors. First, it is not possible to get the current through the galvanometer to be exactly zero. Second, there are always uncertainties in R1 size 12{R rSub { size 8{1} } } {}

, R2 size 12{R rSub { size 8{2} } } {}

, and R3 size 12{R rSub { size 8{3} } } {}

, which contribute to the uncertainty in Rx size 12{R rSub { size 8{x} } } {}

.

Check Your Understanding

Identify other factors that might limit the accuracy of null measurements. Would the use of a digital device that is more sensitive than a galvanometer improve the accuracy of null measurements?

One factor would be resistance in the wires and connections in a null measurement. These are impossible to make zero, and they can change over time. Another factor would be temperature variations in resistance, which can be reduced but not completely eliminated by choice of material. Digital devices sensitive to smaller currents than analog devices do improve the accuracy of null measurements because they allow you to get the current closer to zero.

Section Summary

Conceptual questions

Why can a null measurement be more accurate than one using standard voltmeters and ammeters? What factors limit the accuracy of null measurements?

If a potentiometer is used to measure cell emfs on the order of a few volts, why is it most accurate for the standard emfs size 12{"emf" rSub { size 8{s} } } {}

to be the same order of magnitude and the resistances to be in the range of a few ohms?

Problem Exercises

What is the emfx size 12{"emf" rSub { size 8{x} } } {}

of a cell being measured in a potentiometer, if the standard cell’s emf is 12.0 V and the potentiometer balances for Rx=5.000Ω size 12{R rSub { size 8{x} } =5 "." "000" %OMEGA } {}

and Rs=2.500Ω size 12{R rSub { size 8{s} } =2 "." "500" %OMEGA } {}

?

24.0 V

Calculate the emfx size 12{"emf" rSub { size 8{x} } } {}

of a dry cell for which a potentiometer is balanced when Rx=1.200Ω size 12{R rSub { size 8{x} } =1 "." "200" %OMEGA } {}

, while an alkaline standard cell with an emf of 1.600 V requires Rs=1.247Ω size 12{R rSub { size 8{s} } =1 "." "247" %OMEGA } {}

to balance the potentiometer.

When an unknown resistance Rx size 12{R rSub { size 8{x} } } {}

is placed in a Wheatstone bridge, it is possible to balance the bridge by adjusting R3 size 12{R rSub { size 8{3} } } {}

to be 2500Ω size 12{"2500" %OMEGA } {}

. What is Rx size 12{R rSub { size 8{x} } } {}

if R2R1=0.625 size 12{ { {R rSub { size 8{2} } } over {R rSub { size 8{1} } } } =0 "." "625"} {}

?

1 . 56 k Ω size 12{1 "." "56 k" %OMEGA } {}

To what value must you adjust R3 size 12{R rSub { size 8{3} } } {}

to balance a Wheatstone bridge, if the unknown resistance Rx size 12{R rSub { size 8{x} } } {}

is 100Ω size 12{"100" %OMEGA } {}

, R1 size 12{R rSub { size 8{1} } } {}

is 50.0Ω size 12{"50" "." 0 %OMEGA } {}

, and R2 size 12{R rSub { size 8{2} } } {}

is 175Ω size 12{"175" %OMEGA } {}

?

(a) What is the unknown emfx size 12{"emf" rSub { size 8{x} } } {}

in a potentiometer that balances when Rx size 12{R rSub { size 8{x} } } {}

is 10.0Ω size 12{"10" "." 0 %OMEGA } {}

, and balances when Rs size 12{R rSub { size 8{s} } } {}

is 15.0Ω size 12{"15" "." 0 %OMEGA } {}

for a standard 3.000-V emf? (b) The same emfx size 12{"emf" rSub { size 8{x} } } {}

is placed in the same potentiometer, which now balances when Rs size 12{R rSub { size 8{s} } } {}

is 15.0Ω size 12{"15" "." 0 %OMEGA } {}

for a standard emf of 3.100 V. At what resistance Rx size 12{R rSub { size 8{x} } } {}

will the potentiometer balance?

(a) 2.00 V

(b) 9.68 Ω size 12{9 "." "68 " %OMEGA } {}

Suppose you want to measure resistances in the range from 10.0Ω size 12{"10" "." 0 %OMEGA } {}

to 10.0 kΩ size 12{"10" "." 0" k" %OMEGA } {}

using a Wheatstone bridge that has R2R1=2.000 size 12{ { {R rSub { size 8{2} } } over {R rSub { size 8{1} } } } =2 "." "000"} {}

. Over what range should R3 size 12{R rSub { size 8{3} } } {}

be adjustable?

Range = 5 . 00 Ω to 5 . 00 k Ω size 12{"Range=5" "." "00 " %OMEGA " to "5 "." "00"" k" %OMEGA } {}

Glossary

null measurements
methods of measuring current and voltage more accurately by balancing the circuit so that no current flows through the measurement device
potentiometer
a null measurement device for measuring potentials (voltages)
ohmmeter
an instrument that applies a voltage to a resistance, measures the current, calculates the resistance using Ohm’s law, and provides a readout of this calculated resistance
bridge device
a device that forms a bridge between two branches of a circuit; some bridge devices are used to make null measurements in circuits
Wheatstone bridge
a null measurement device for calculating resistance by balancing potential drops in a circuit
Creative Commons License
This work is licensed under a Creative Commons Attribution 4.0 International License.

You can also download for free at http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@11.1

Attribution: