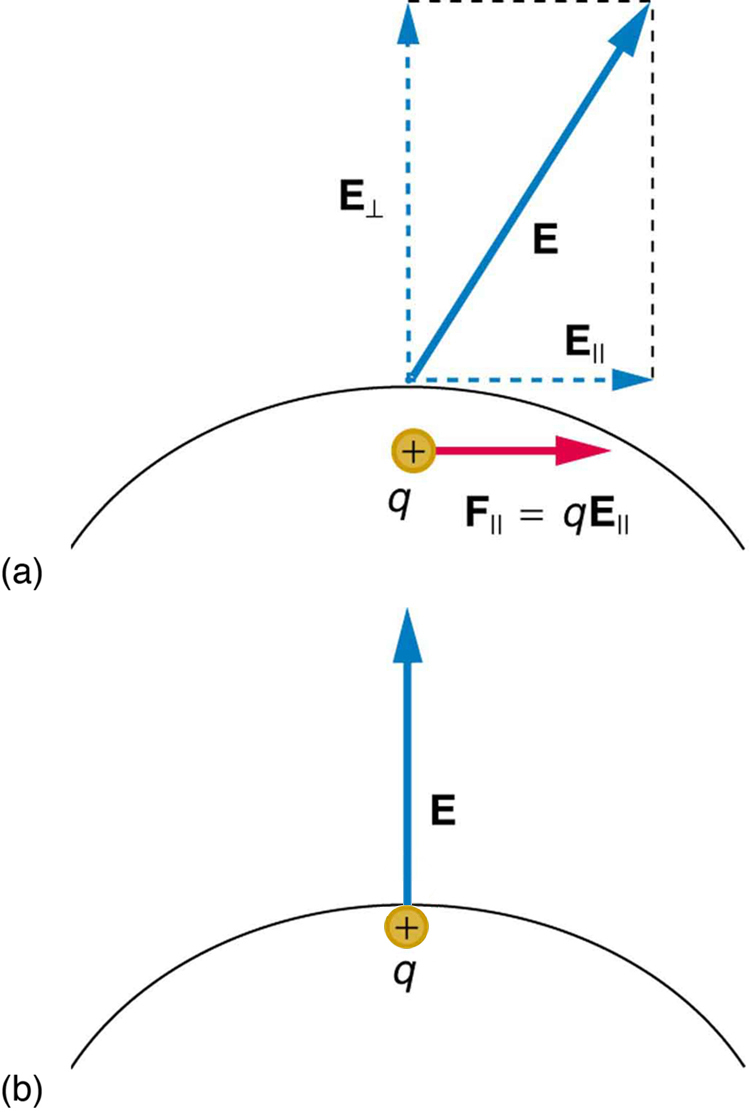
Conductors and Electric Fields in Static Equilibrium

Conductors contain free charges that move easily. When excess charge is placed on a conductor or the conductor is put into a static electric field, charges in the conductor quickly respond to reach a steady state called electrostatic equilibrium.

[link] shows the effect of an electric field on free charges in a conductor. The free charges move until the field is perpendicular to the conductor’s surface. There can be no component of the field parallel to the surface in electrostatic equilibrium, since, if there were, it would produce further movement of charge. A positive free charge is shown, but free charges can be either positive or negative and are, in fact, negative in metals. The motion of a positive charge is equivalent to the motion of a negative charge in the opposite direction.

In part a, an electric field E exists at some angle with the horizontal applied on a conductor. One component of this field E parallel is along x axis represented by a vector arrow and other E perpendicular, is along y axis represented by a vector arrow. Charge inside the conductor moves along x axis so the force acting on it is F parallel, which is equal to q multiplied by E parallel. In part b, a charge is shown inside the conductor and electric field is represented by a vector arrow pointing upward starting from the surface of the conductor.

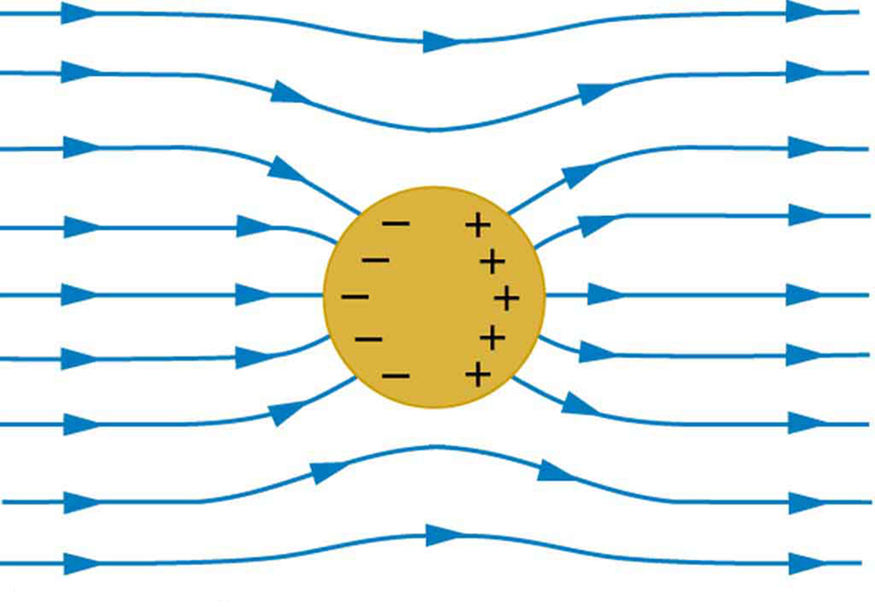
A conductor placed in an electric field will be polarized. [link] shows the result of placing a neutral conductor in an originally uniform electric field. The field becomes stronger near the conductor but entirely disappears inside it.

A spherical conductor is placed in the external electric field. The field lines are shown running from left to right. The field lines enter and leave the conductor at right angles. Negative charges accumulate on the left surface of the conductor and positive charges accumulate on the right surface of the conductor.

Misconception Alert: Electric Field inside a Conductor

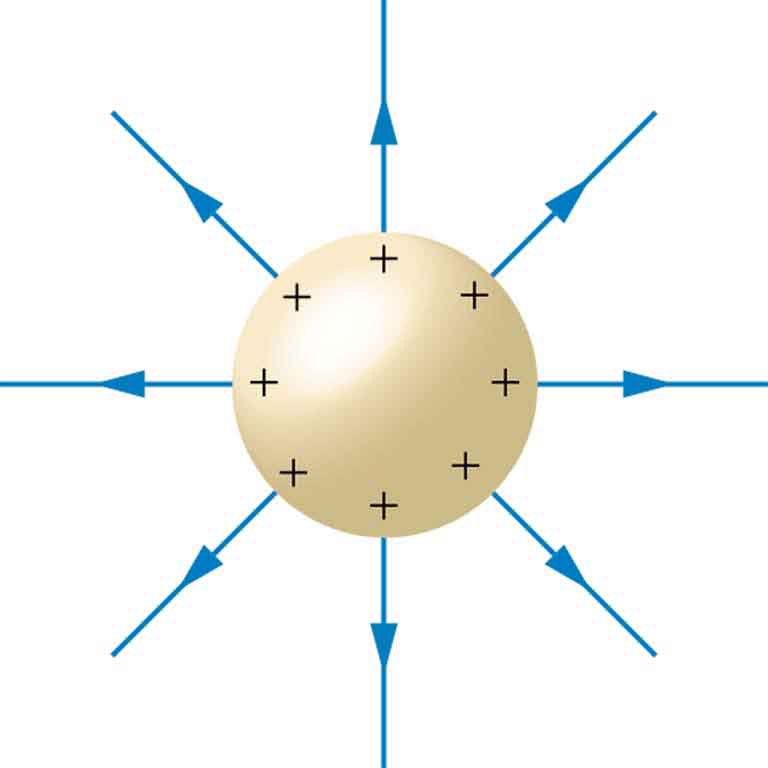
Excess charges placed on a spherical conductor repel and move until they are evenly distributed, as shown in [link]. Excess charge is forced to the surface until the field inside the conductor is zero. Outside the conductor, the field is exactly the same as if the conductor were replaced by a point charge at its center equal to the excess charge.

A positively charged sphere is shown and positive charges are distributed all over the surface. Electric field lines emanate from the sphere in the space shown by the vector arrow pointing outward.

Properties of a Conductor in Electrostatic Equilibrium
  1. The electric field is zero inside a conductor.
  2. Just outside a conductor, the electric field lines are perpendicular to its surface, ending or beginning on charges on the surface.
  3. Any excess charge resides entirely on the surface or surfaces of a conductor.

The properties of a conductor are consistent with the situations already discussed and can be used to analyze any conductor in electrostatic equilibrium. This can lead to some interesting new insights, such as described below.

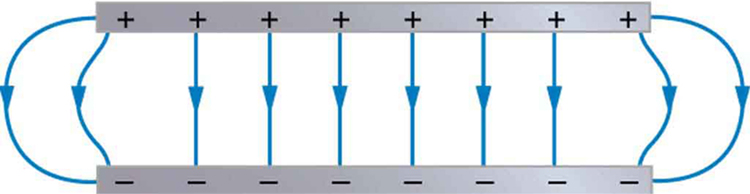
How can a very uniform electric field be created? Consider a system of two metal plates with opposite charges on them, as shown in [link]. The properties of conductors in electrostatic equilibrium indicate that the electric field between the plates will be uniform in strength and direction. Except near the edges, the excess charges distribute themselves uniformly, producing field lines that are uniformly spaced (hence uniform in strength) and perpendicular to the surfaces (hence uniform in direction, since the plates are flat). The edge effects are less important when the plates are close together.

Two charged metal plates are shown. The lower plate has negative charge and the upper plate has positive charge. The electric field lines start from positive plate and enter the negative plate represented by arrows.

Earth’s Electric Field

A near uniform electric field of approximately 150 N/C, directed downward, surrounds Earth, with the magnitude increasing slightly as we get closer to the surface. What causes the electric field? At around 100 km above the surface of Earth we have a layer of charged particles, called the ionosphere. The ionosphere is responsible for a range of phenomena including the electric field surrounding Earth. In fair weather the ionosphere is positive and the Earth largely negative, maintaining the electric field ([link](a)).

In storm conditions clouds form and localized electric fields can be larger and reversed in direction ([link](b)). The exact charge distributions depend on the local conditions, and variations of [link](b) are possible.

If the electric field is sufficiently large, the insulating properties of the surrounding material break down and it becomes conducting. For air this occurs at around 3×106 size 12{3 times "10" rSup { size 8{6} } } {}

N/C. Air ionizes ions and electrons recombine, and we get discharge in the form of lightning sparks and corona discharge.

In part a, a child is flying a kite with two men in an open field on a bright sunny day. In part b, lightning appears over a body of water in stormy weather.

Electric Fields on Uneven Surfaces

So far we have considered excess charges on a smooth, symmetrical conductor surface. What happens if a conductor has sharp corners or is pointed? Excess charges on a nonuniform conductor become concentrated at the sharpest points. Additionally, excess charge may move on or off the conductor at the sharpest points.

To see how and why this happens, consider the charged conductor in [link]. The electrostatic repulsion of like charges is most effective in moving them apart on the flattest surface, and so they become least concentrated there. This is because the forces between identical pairs of charges at either end of the conductor are identical, but the components of the forces parallel to the surfaces are different. The component parallel to the surface is greatest on the flattest surface and, hence, more effective in moving the charge.

The same effect is produced on a conductor by an externally applied electric field, as seen in [link] (c). Since the field lines must be perpendicular to the surface, more of them are concentrated on the most curved parts.

In part a, a conductor is shown with the unsymmetrical shape. The identical pair of charges at opposite ends on the conductor have similar components of forces represented by arrows. In part b, the unsymmetrical object has positive charge on its surface. The electric field lines are shown emerging perpendicular from the surface of the conductor represented by vector arrow. In part c, the field lines in and around the conductor running from left to right is shown. The left surface of the conductor has negative charge and the right surface has positive charge. The field lines enter and leave the conductor at right angles.

Applications of Conductors

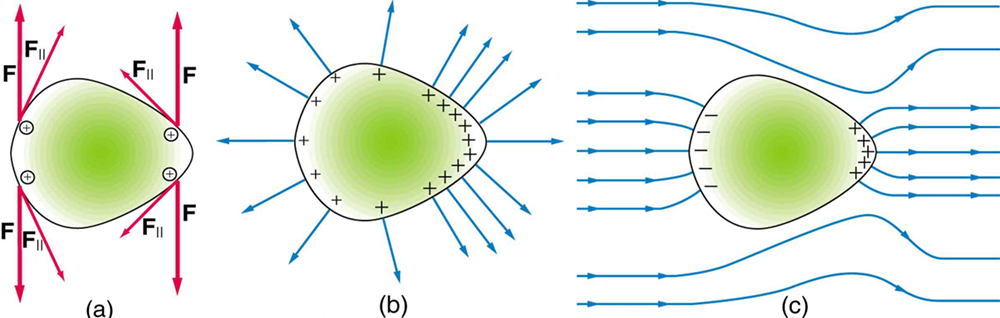
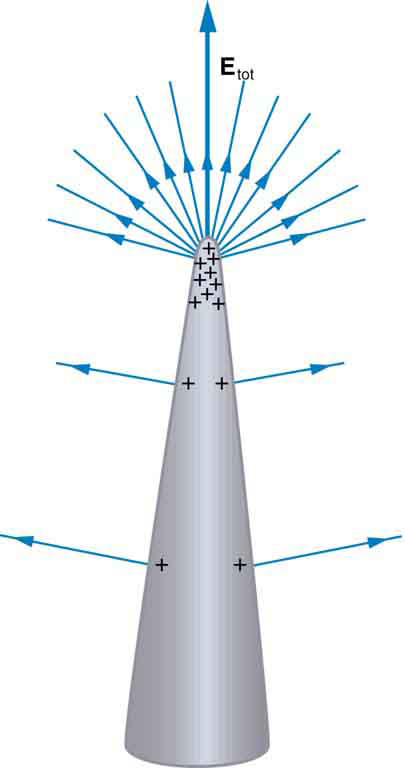
On a very sharply curved surface, such as shown in [link], the charges are so concentrated at the point that the resulting electric field can be great enough to remove them from the surface. This can be useful.

Lightning rods work best when they are most pointed. The large charges created in storm clouds induce an opposite charge on a building that can result in a lightning bolt hitting the building. The induced charge is bled away continually by a lightning rod, preventing the more dramatic lightning strike.

Of course, we sometimes wish to prevent the transfer of charge rather than to facilitate it. In that case, the conductor should be very smooth and have as large a radius of curvature as possible. (See [link].) Smooth surfaces are used on high-voltage transmission lines, for example, to avoid leakage of charge into the air.

Another device that makes use of some of these principles is a Faraday cage. This is a metal shield that encloses a volume. All electrical charges will reside on the outside surface of this shield, and there will be no electrical field inside. A Faraday cage is used to prohibit stray electrical fields in the environment from interfering with sensitive measurements, such as the electrical signals inside a nerve cell.

During electrical storms if you are driving a car, it is best to stay inside the car as its metal body acts as a Faraday cage with zero electrical field inside. If in the vicinity of a lightning strike, its effect is felt on the outside of the car and the inside is unaffected, provided you remain totally inside. This is also true if an active (“hot”) electrical wire was broken (in a storm or an accident) and fell on your car.

A cone shaped positively charged conductor is shown where most of the positive charges are accumulated at the tip. The field lines represented by arrows emerge at right angles from the surface of the conductor in outward direction. The density of field lines is greater at the tip of the cone than at other surfaces.

In part a, a lightning rod is shown on the roof of a house. In part b, a person is touching the metal sphere of the Van De Graaff and his hair is standing up.

Section Summary

Conceptual Questions

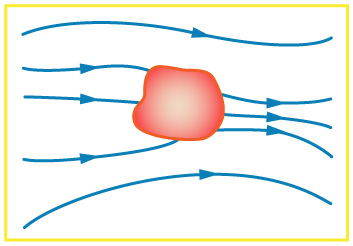
Is the object in [link] a conductor or an insulator? Justify your answer.

External field lines entering the object from one end and emerging from another are shown by lines.{:}

If the electric field lines in the figure above were perpendicular to the object, would it necessarily be a conductor? Explain.

The discussion of the electric field between two parallel conducting plates, in this module states that edge effects are less important if the plates are close together. What does close mean? That is, is the actual plate separation crucial, or is the ratio of plate separation to plate area crucial?

Would the self-created electric field at the end of a pointed conductor, such as a lightning rod, remove positive or negative charge from the conductor? Would the same sign charge be removed from a neutral pointed conductor by the application of a similar externally created electric field? (The answers to both questions have implications for charge transfer utilizing points.)

Why is a golfer with a metal club over her shoulder vulnerable to lightning in an open fairway? Would she be any safer under a tree?

Can the belt of a Van de Graaff accelerator be a conductor? Explain.

Are you relatively safe from lightning inside an automobile? Give two reasons.

Discuss pros and cons of a lightning rod being grounded versus simply being attached to a building.

Using the symmetry of the arrangement, show that the net Coulomb force on the charge *q size 12{q} {}

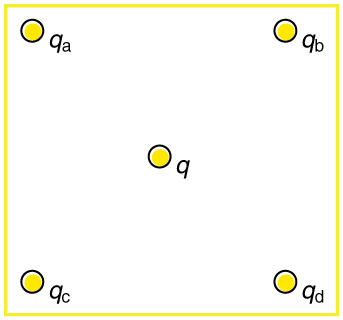
Four point charges, one is q a, second is q b, third is q c, and fourth is q d, lie on the corners of a square. q is located at its center.

(a) Using the symmetry of the arrangement, show that the electric field at the center of the square in [link] is zero if the charges on the four corners are exactly equal. (b) Show that this is also true for any combination of charges in which qa=qd size 12{q rSub { size 8{a} } =q rSub { size 8{d} } } {}

and qb=qc size 12{q rSub { size 8{b} } =q rSub { size 8{z} } } {}

(a) What is the direction of the total Coulomb force on q size 12{q} {}

in [link] if q size 12{q} {}

is negative, qa=qc size 12{q rSub { size 8{a} } =q rSub { size 8{c} } } {}

and both are negative, and qb=qc size 12{q rSub { size 8{b} } =q rSub { size 8{c} } } {}

and both are positive? (b) What is the direction of the electric field at the center of the square in this situation?

Considering [link], suppose that qa=qd size 12{q rSub { size 8{a} } =q rSub { size 8{d} } } {}

and qb=qc size 12{q rSub { size 8{b} } =q rSub { size 8{c} } } {}

. First show that *q size 12{q} {}

If qa=0 size 12{q rSub { size 8{a} } =0} {}

in [link], under what conditions will there be no net Coulomb force on *q size 12{q} {}

*?

In regions of low humidity, one develops a special “grip” when opening car doors, or touching metal door knobs. This involves placing as much of the hand on the device as possible, not just the ends of one’s fingers. Discuss the induced charge and explain why this is done.

Tollbooth stations on roadways and bridges usually have a piece of wire stuck in the pavement before them that will touch a car as it approaches. Why is this done?

Suppose a woman carries an excess charge. To maintain her charged status can she be standing on ground wearing just any pair of shoes? How would you discharge her? What are the consequences if she simply walks away?

Problems & Exercises

Sketch the electric field lines in the vicinity of the conductor in [link] given the field was originally uniform and parallel to the object’s long axis. Is the resulting field small near the long side of the object?

A oblong-shaped conductor.{:}

Sketch the electric field lines in the vicinity of the conductor in [link] given the field was originally uniform and parallel to the object’s long axis. Is the resulting field small near the long side of the object?

A oblong-shaped conductor.{:}

Sketch the electric field between the two conducting plates shown in [link], given the top plate is positive and an equal amount of negative charge is on the bottom plate. Be certain to indicate the distribution of charge on the plates.

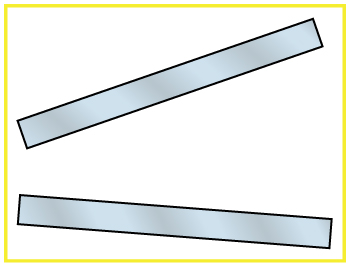Two plates are shown; one is in horizontal direction and other is above the first plate with some inclination.{:}

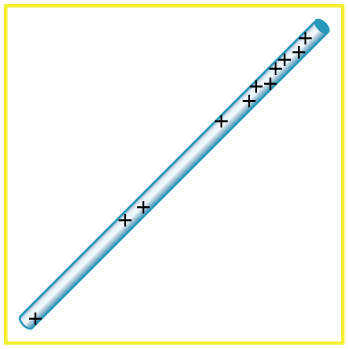
Sketch the electric field lines in the vicinity of the charged insulator in [link] noting its nonuniform charge distribution.

A positively charged rod with a concentration of positive charges near the top and a few in the middle.

What is the force on the charge located at x=8.00 cm

in [link](a) given that q=1.00μC size 12{q=1 "." "00""μC"} {}

?

Three point charges are shown on the scaling line. First charge plus q is at three point zero, second charge minus two q is at eight point zero, and third charge plus q is eleven point zero centimeters along the x axis. Four charges are placed on a scaling line. First is minus two q at one point zero, second is plus q at five point zero, third is plus three q is at eight point zero, and fourth is minus q placed at fourteen point zero centimeter along the x axis.{:}

(a) Find the total electric field at x=1.00 cm

in [link](b) given that q=5.00 nC

. (b) Find the total electric field at x=11.00 cm

in [link](b). (c) If the charges are allowed to move and eventually be brought to rest by friction, what will the final charge configuration be? (That is, will there be a single charge, double charge, etc., and what will its value(s) be?)

(a) Ex=1.00 cm=−∞ size 12{E rSub { size 8{x=1 "." "00" ital "cm"} } = - infinity } {}

(b) 2.12×105N/C size 12{ {underline {2 "." "12" times "10" rSup { size 8{5} } " N/C" {underline {}} }} } {}

(c) one charge of +q

(a) Find the electric field at x=5.00 cm

in [link](a), given that q=1.00μC size 12{q=1 "." "00""μC"} {}

. (b) At what position between 3.00 and 8.00 cm is the total electric field the same as that for –2q

alone? (c) Can the electric field be zero anywhere between 0.00 and 8.00 cm? (d) At very large positive or negative values of x, the electric field approaches zero in both (a) and (b). In which does it most rapidly approach zero and why? (e) At what position to the right of 11.0 cm is the total electric field zero, other than at infinity? (Hint: A graphing calculator can yield considerable insight in this problem.)

(a) Find the total Coulomb force on a charge of 2.00 nC located at x=4.00 cm

in [link] (b), given that q=1.00μC size 12{q=1 "." "00""μC"} {}

. (b) Find the x-position at which the electric field is zero in [link] (b).

(a) 0.252 N to the left

(b) x=6.07 cm

Using the symmetry of the arrangement, determine the direction of the force on q size 12{q} {}

in the figure below, given that qa=qb=+7.50μC size 12{q rSub { size 8{a} } =q rSub { size 8{b} } "=+"7 "." "50""μC"} {}

and qc=qd=−7.50μC size 12{q rSub { size 8{c} } =q rSub { size 8{d} } = - 7 "." "50""μC"} {}

. (b) Calculate the magnitude of the force on the charge *q size 12{q} {}

*, given that the square is 10.0 cm on a side and q=2.00μC size 12{q=2 "." "00""μC"} {}

.

Four point charges, one is q a, second is q b, third is q c, and fourth is q d, lie on the corners of a square. q is located at its center.

(a) Using the symmetry of the arrangement, determine the direction of the electric field at the center of the square in [link], given that qa=qb=−1.00μC size 12{q rSub { size 8{a} } =q rSub { size 8{b} } = - 1 "." "00""μC"} {}

and qc=qd=+1.00μC size 12{q rSub { size 8{c} } =q rSub { size 8{d} } "=+"1 "." "00""μC"} {}

. (b) Calculate the magnitude of the electric field at the location of q size 12{q} {}

, given that the square is 5.00 cm on a side.

(a)The electric field at the center of the square will be straight up, since qa size 12{q rSub { size 8{a} } } {}

and qb size 12{q rSub { size 8{b} } } {}

are positive and qc size 12{q rSub { size 8{c} } } {}

and qd size 12{q rSub { size 8{d} } } {}

are negative and all have the same magnitude.

(b) 2.04×107N/C(upward) size 12{ {underline {2 "." "04" times "10" rSup { size 8{7} } " N/C" \( "upward" \) }} } {}

Find the electric field at the location of qa size 12{q rSub { size 8{a} } } {}

in [link] given that qb=qc=qd=+2.00nC size 12{q rSub { size 8{b} } =q rSub { size 8{c} } =q rSub { size 8{d} } "=+"2 "." "00""nC"} {}

, q=−1.00nC size 12{q= - 1 "." "00""nC"} {}

, and the square is 20.0 cm on a side.

Find the total Coulomb force on the charge q

in [link], given that q=1.00μC size 12{q=1 "." "00""μC"} {}

, qa=2.00μC size 12{q rSub { size 8{a} } =2 "." "00""μC"} {}

, qb=−3.00μC size 12{q rSub { size 8{b} } = - 3 "." "00""μC"} {}

, qc=−4.00μC size 12{q rSub { size 8{c} } = - 4 "." "00""μC"} {}

, and qd=+1.00μC size 12{q rSub { size 8{d} } "=+"1 "." "00""μC"} {}

. The square is 50.0 cm on a side.

0.102N, size 12{0 "." "102"" N",} {}

in the −y size 12{ - y ital } {}

{} {} {}

direction

(a) Find the electric field at the location of qa

in [link], given that qb=+10.00μC

and qc=–5.00μC

. (b) What is the force on qa

, given that qa=+1.50nC

?

Three point charges located at the corners of an equilateral triangle.

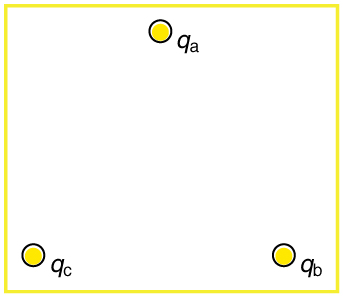
(a) Find the electric field at the center of the triangular configuration of charges in [link], given that qa=+2.50nC size 12{q rSub { size 8{a} } "=+"2 "." "50""nC"} {}

, qb=−8.00nC size 12{q rSub { size 8{b} } = - 8 "." "00""nC"} {}

, and qc=+1.50nC size 12{q rSub { size 8{c} } "=+"1 "." "50""nC"} {}

. (b) Is there any combination of charges, other than qa=qb=qc size 12{q rSub { size 8{a} } =q rSub { size 8{b} } =q rSub { size 8{c} } } {}

, that will produce a zero strength electric field at the center of the triangular configuration?

(a) E→=4.36×103N/C,35.0º

, below the horizontal.

(b) No

Glossary

conductor
an object with properties that allow charges to move about freely within it
free charge
an electrical charge (either positive or negative) which can move about separately from its base molecule
electrostatic equilibrium
an electrostatically balanced state in which all free electrical charges have stopped moving about
polarized
a state in which the positive and negative charges within an object have collected in separate locations
ionosphere
a layer of charged particles located around 100 km above the surface of Earth, which is responsible for a range of phenomena including the electric field surrounding Earth
Faraday cage
a metal shield which prevents electric charge from penetrating its surface
Creative Commons License
This work is licensed under a Creative Commons Attribution 4.0 International License.

You can also download for free at http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@11.1

Attribution: