Collisions of Point Masses in Two Dimensions

Discuss two dimensional collisions as an extension of one dimensional analysis.
Define point masses.
Derive an expression for conservation of momentum along x-axis and y-axis.
Describe elastic collisions of two objects with equal mass.
Determine the magnitude and direction of the final velocity given initial velocity, and scattering angle.

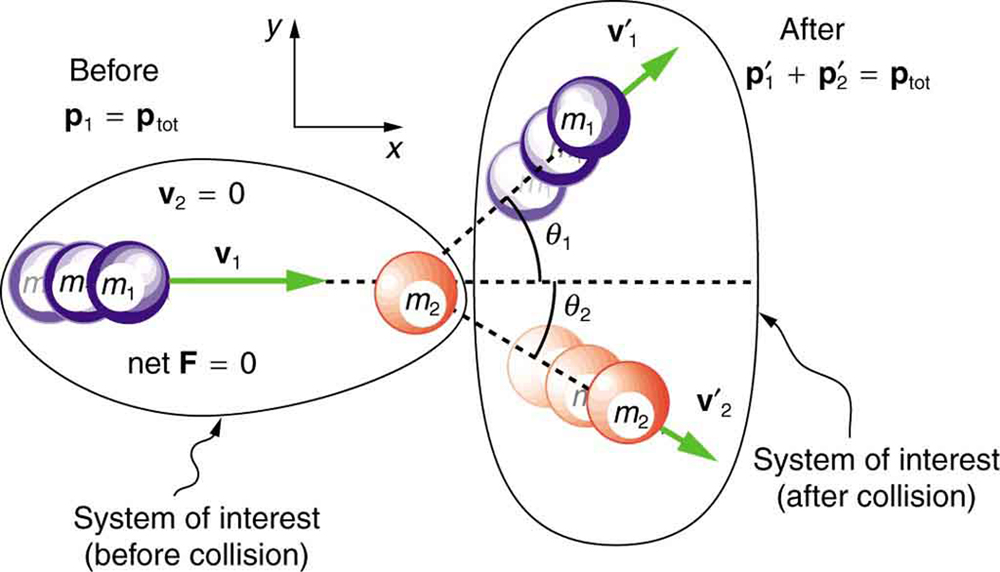
In the previous two sections, we considered only one-dimensional collisions; during such collisions, the incoming and outgoing velocities are all along the same line. But what about collisions, such as those between billiard balls, in which objects scatter to the side? These are two-dimensional collisions, and we shall see that their study is an extension of the one-dimensional analysis already presented. The approach taken (similar to the approach in discussing two-dimensional kinematics and dynamics) is to choose a convenient coordinate system and resolve the motion into components along perpendicular axes. Resolving the motion yields a pair of one-dimensional problems to be solved simultaneously.

One complication arising in two-dimensional collisions is that the objects might rotate before or after their collision. For example, if two ice skaters hook arms as they pass by one another, they will spin in circles. We will not consider such rotation until later, and so for now we arrange things so that no rotation is possible. To avoid rotation, we consider only the scattering of point masses—that is, structureless particles that cannot rotate or spin.

We start by assuming that $F_{net} = 0$

, so that momentum $p$

is conserved. The simplest collision is one in which one of the particles is initially at rest. (See [link].) The best choice for a coordinate system is one with an axis parallel to the velocity of the incoming particle, as shown in [link]. Because momentum is conserved, the components of momentum along the $x$

and $y$

-axes $(p_{x} and p_{y})$

will also be conserved, but with the chosen coordinate system, $p_{y}$

is initially zero and $p_{x}$

is the momentum of the incoming particle. Both facts simplify the analysis. (Even with the simplifying assumptions of point masses, one particle initially at rest, and a convenient coordinate system, we still gain new insights into nature from the analysis of two-dimensional collisions.)

Along the $x$

-axis, the equation for conservation of momentum is

p_{1 x} + p_{2 x} = {p'}_{1 x} + {p'}_{2 x} .

Where the subscripts denote the particles and axes and the primes denote the situation after the collision. In terms of masses and velocities, this equation is

m_{1} v_{1 x} + m_{2} v_{2 x} = m_{1} {v'}_{1 x} + m_{2} {v'}_{2 x} .

But because particle 2 is initially at rest, this equation becomes

m_{1} v_{1 x} = m_{1} {v'}_{1 x} + m_{2} {v'}_{2 x} .

The components of the velocities along the $x$

-axis have the form $v cos θ$

. Because particle 1 initially moves along the $x$

-axis, we find $v_{1 x} = v_{1}$

Conservation of momentum along the $x$

-axis gives the following equation:

m_{1} v_{1} = m_{1} {v'}_{1} cos θ_{1} + m_{2} {v'}_{2} cos θ_{2},

where $θ_{1}$

and $θ_{2}$

are as shown in [link].

Conservation of Momentum along the *

x

*-axis

m_{1} v_{1} = m_{1} {v'}_{1} cos θ_{1} + m_{2} {v'}_{2} cos θ_{2}

Along the $y$

-axis, the equation for conservation of momentum is

p_{1 y} + p_{2 y} = {p'}_{1 y} + {p'}_{2 y}

m_{1} v_{1 y} + m_{2} v_{2 y} = m_{1} {v'}_{1 y} + m_{2} {v'}_{2 y} .

But $v_{1 y}$

is zero, because particle 1 initially moves along the $x$

-axis. Because particle 2 is initially at rest, $v_{2 y}$

is also zero. The equation for conservation of momentum along the $y$

-axis becomes

0 = m_{1} {v'}_{1 y} + m_{2} {v'}_{2 y} .

The components of the velocities along the $y$

-axis have the form $v sin θ$

Thus, conservation of momentum along the $y$

-axis gives the following equation:

0 = m_{1} {v'}_{1} sin θ_{1} + m_{2} {v'}_{2} sin θ_{2} .

Conservation of Momentum along the

y

-axis

0 = m_{1} {v'}_{1} sin θ_{1} + m_{2} {v'}_{2} sin θ_{2}

The equations of conservation of momentum along the * $x$

*-axis and $y$

-axis are very useful in analyzing two-dimensional collisions of particles, where one is originally stationary (a common laboratory situation). But two equations can only be used to find two unknowns, and so other data may be necessary when collision experiments are used to explore nature at the subatomic level.

Determining the Final Velocity of an Unseen Object from the Scattering of Another Object

Suppose the following experiment is performed. A 0.250-kg object $(m_{1})$

is slid on a frictionless surface into a dark room, where it strikes an initially stationary object with mass of 0.400 kg $(m_{2})$

. The 0.250-kg object emerges from the room at an angle of $45 . 0º$

with its incoming direction.

The speed of the 0.250-kg object is originally 2.00 m/s and is 1.50 m/s after the collision. Calculate the magnitude and direction of the velocity $({v'}_{2}$

and $θ_{2})$

of the 0.400-kg object after the collision.

Strategy

Momentum is conserved because the surface is frictionless. The coordinate system shown in [link] is one in which $m_{2}$

is originally at rest and the initial velocity is parallel to the $x$

-axis, so that conservation of momentum along the $x$

and * $y$

*-axes is applicable.

Everything is known in these equations except ${v'}_{2}$

and $θ_{2}$

, which are precisely the quantities we wish to find. We can find two unknowns because we have two independent equations: the equations describing the conservation of momentum in the $x$

and $y$

-directions.

Solution

Solving $m_{1} v_{1} = m_{1} {v'}_{1} cos θ_{1} + m_{2} {v'}_{2} cos θ_{2}$

for $v_{2}^{'} cos θ_{2}$

and $0 = m_{1} {v'}_{1} sin θ_{1} + m_{2} {v'}_{2} sin θ_{2}$

for ${v'}_{2} sin θ_{2}$

and taking the ratio yields an equation (in which θ₂ is the only unknown quantity. Applying the identity $(tan θ = \frac{sin θ}{cos θ})$

, we obtain:

tan θ_{2} = \frac{{v'}_{1} sin θ_{1}}{{v'}_{1} cos θ_{1} - v_{1}} .

Entering known values into the previous equation gives

tan θ_{2} = \frac{(1.50 m/s) (0.7071)}{(1.50 m/s) (0.7071) - 2 . 00 m/s} = - 1 . 129 .

Thus,

θ_{2} = {tan}^{- 1} (- 1 . 129) = 311 . 5º \approx 312º .

Angles are defined as positive in the counter clockwise direction, so this angle indicates that $m_{2}$

is scattered to the right in [link], as expected (this angle is in the fourth quadrant). Either equation for the $x$

or $y$

-axis can now be used to solve for ${v'}_{2}$

, but the latter equation is easiest because it has fewer terms.

{v'}_{2} = - \frac{m_{1}}{m_{2}} {v'}_{1} \frac{sin θ_{1}}{sin θ_{2}}

Entering known values into this equation gives

{v'}_{2} = - (\frac{0.250 kg}{0.400 kg}) (1.50 m/s) (\frac{0.7071}{- 0 . 7485}) .

Thus,

{v'}_{2} = 0 . 886 m/s .

Discussion

It is instructive to calculate the internal kinetic energy of this two-object system before and after the collision. (This calculation is left as an end-of-chapter problem.) If you do this calculation, you will find that the internal kinetic energy is less after the collision, and so the collision is inelastic. This type of result makes a physicist want to explore the system further.

Elastic Collisions of Two Objects with Equal Mass

Some interesting situations arise when the two colliding objects have equal mass and the collision is elastic. This situation is nearly the case with colliding billiard balls, and precisely the case with some subatomic particle collisions. We can thus get a mental image of a collision of subatomic particles by thinking about billiards (or pool). (Refer to [link] for masses and angles.) First, an elastic collision conserves internal kinetic energy. Again, let us assume object 2 $(m_{2})$

is initially at rest. Then, the internal kinetic energy before and after the collision of two objects that have equal masses is

\frac{1}{2} {mv}_{1}^{2} = \frac{1}{2} {mv'}_{1}^{2} + \frac{1}{2} {mv'}_{2}^{2} .

Because the masses are equal, $m_{1} = m_{2} = m$

. Algebraic manipulation (left to the reader) of conservation of momentum in the $x$

and * $y$

*-directions can show that

\frac{1}{2} {mv}_{1}^{2} = \frac{1}{2} {mv'}_{1}^{2} + \frac{1}{2} {mv'}_{2}^{2} + {mv'}_{1} {v'}_{2} cos (θ_{1} - θ_{2}) .

(Remember that $θ_{2}$

is negative here.) The two preceding equations can both be true only if

m {v'}_{1} {v'}_{2} cos (θ_{1} - θ_{2}) = 0 .

There are three ways that this term can be zero. They are

${v'}_{1} = 0$
: head-on collision; incoming ball stops
${v'}_{2} = 0$
: no collision; incoming ball continues unaffected
$cos (θ_{1} - θ_{2}) = 0$
: angle of separation
$(θ_{1} - θ_{2})$
is
$90º$
after the collision

All three of these ways are familiar occurrences in billiards and pool, although most of us try to avoid the second. If you play enough pool, you will notice that the angle between the balls is very close to $90º$

after the collision, although it will vary from this value if a great deal of spin is placed on the ball. (Large spin carries in extra energy and a quantity called angular momentum, which must also be conserved.) The assumption that the scattering of billiard balls is elastic is reasonable based on the correctness of the three results it produces. This assumption also implies that, to a good approximation, momentum is conserved for the two-ball system in billiards and pool. The problems below explore these and other characteristics of two-dimensional collisions.

Connections to Nuclear and Particle Physics

Two-dimensional collision experiments have revealed much of what we know about subatomic particles, as we shall see in Medical Applications of Nuclear Physics and Particle Physics. Ernest Rutherford, for example, discovered the nature of the atomic nucleus from such experiments.

Section Summary

The approach to two-dimensional collisions is to choose a convenient coordinate system and break the motion into components along perpendicular axes. Choose a coordinate system with the $x$
-axis parallel to the velocity of the incoming particle.
Two-dimensional collisions of point masses where mass 2 is initially at rest conserve momentum along the initial direction of mass 1 (the $x$
-axis), stated by
$m_{1} v_{1} = m_{1} {v'}_{1} cos θ_{1} + m_{2} {v'}_{2} cos θ_{2}$
and along the direction perpendicular to the initial direction (the
$y$
-axis) stated by
$0 = m_{1} {v'}_{1 y} + m_{2} {v'}_{2 y}$
.
The internal kinetic before and after the collision of two objects that have equal masses is
$\frac{1}{2} {mv}_{1}^{2} = \frac{1}{2} {mv'}_{1}^{2} + \frac{1}{2} {mv'}_{2}^{2} + {mv'}_{1} {v'}_{2} cos (θ_{1} - θ_{2}) .$
Point masses are structureless particles that cannot spin.

Conceptual Questions

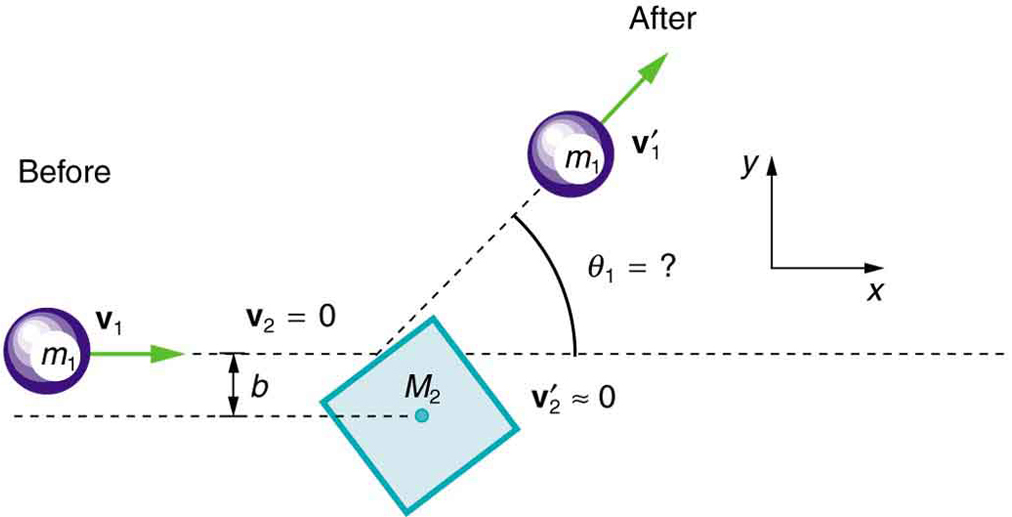
[link] shows a cube at rest and a small object heading toward it. (a) Describe the directions (angle $θ_{1}$

) at which the small object can emerge after colliding elastically with the cube. How does $θ_{1}$

depend on $b$

, the so-called impact parameter? Ignore any effects that might be due to rotation after the collision, and assume that the cube is much more massive than the small object. (b) Answer the same questions if the small object instead collides with a massive sphere.

Problems & Exercises

Two identical pucks collide on an air hockey table. One puck was originally at rest. (a) If the incoming puck has a speed of 6.00 m/s and scatters to an angle of $30 . 0º$

,what is the velocity (magnitude and direction) of the second puck? (You may use the result that $θ_{1} - θ_{2} = 90º$

for elastic collisions of objects that have identical masses.) (b) Confirm that the collision is elastic.

(a) 3.00 m/s, $60º$

below $x$

-axis

(b) Find speed of first puck after collision: $0 = m {v'}_{1} sin 30º - m {v'}_{2} sin 60º \Rightarrow {v'}_{1} = {v'}_{2} \frac{sin 60º}{sin 30º} = 5.196 m/s$

Verify that ratio of initial to final KE equals one: $\begin{array}{l} KE = \frac{1}{2} {mv}_{1}^{2} = 18 m J \\ KE = \frac{1}{2} {mv'}_{1}^{2} + \frac{1}{2} {mv'}_{2}^{2} = 18 m J \end{array}\} \frac{KE}{KE′} = 1.00$

Confirm that the results of the example [link] do conserve momentum in both the * $x$

*- and * $y$

*-directions.

A 3000-kg cannon is mounted so that it can recoil only in the horizontal direction. (a) Calculate its recoil velocity when it fires a 15.0-kg shell at 480 m/s at an angle of $20 . 0º$

above the horizontal. (b) What is the kinetic energy of the cannon? This energy is dissipated as heat transfer in shock absorbers that stop its recoil. (c) What happens to the vertical component of momentum that is imparted to the cannon when it is fired?

(a) $- 2 . 26 m/s$

(b) $7 . 63 \times 10^{3} J$

(c) The ground will exert a normal force to oppose recoil of the cannon in the vertical direction. The momentum in the vertical direction is transferred to the earth. The energy is transferred into the ground, making a dent where the cannon is. After long barrages, cannon have erratic aim because the ground is full of divots.

Professional Application

A 5.50-kg bowling ball moving at 9.00 m/s collides with a 0.850-kg bowling pin, which is scattered at an angle of $85 . 0º$

to the initial direction of the bowling ball and with a speed of 15.0 m/s. (a) Calculate the final velocity (magnitude and direction) of the bowling ball. (b) Is the collision elastic? (c) Linear kinetic energy is greater after the collision. Discuss how spin on the ball might be converted to linear kinetic energy in the collision.

Professional Application

Ernest Rutherford (the first New Zealander to be awarded the Nobel Prize in Chemistry) demonstrated that nuclei were very small and dense by scattering helium-4 nuclei $(^{4} He)$

from gold-197 nuclei $(^{197} Au)$

. The energy of the incoming helium nucleus was $8.00 \times 10^{- 13} J$

, and the masses of the helium and gold nuclei were $6.68 \times 10^{- 27} kg$

and $3.29 \times 10^{- 25} kg$

, respectively (note that their mass ratio is 4 to 197). (a) If a helium nucleus scatters to an angle of $120º$

during an elastic collision with a gold nucleus, calculate the helium nucleus’s final speed and the final velocity (magnitude and direction) of the gold nucleus. (b) What is the final kinetic energy of the helium nucleus?

(a) $5 . 36 \times 10^{5} m/s$

at $- 29.5º$

(b) $7 . 52 \times 10^{- 13} J$

Professional Application

Two cars collide at an icy intersection and stick together afterward. The first car has a mass of 1200 kg and is approaching at $8.00 m/s$

due south. The second car has a mass of 850 kg and is approaching at $17.0 m/s$

due west. (a) Calculate the final velocity (magnitude and direction) of the cars. (b) How much kinetic energy is lost in the collision? (This energy goes into deformation of the cars.) Note that because both cars have an initial velocity, you cannot use the equations for conservation of momentum along the * $x$

*-axis and $y$

-axis; instead, you must look for other simplifying aspects.

Starting with equations $m_{1} v_{1} = m_{1} {v'}_{1} cos θ_{1} + m_{2} {v'}_{2} cos θ_{2}$

and $0 = m_{1} {v'}_{1} sin θ_{1} + m_{2} {v'}_{2} sin θ_{2}$

for conservation of momentum in the $x$

and $y$

-directions and assuming that one object is originally stationary, prove that for an elastic collision of two objects of equal masses,

\frac{1}{2} {mv}_{1}^{2} = \frac{1}{2} {mv'}_{1}^{2} + \frac{1}{2} {mv'}_{2}^{2} + {mv'}_{1} {v'}_{2} cos (θ_{1} - θ_{2})

as discussed in the text.

We are given that $m_{1} = m_{2} \equiv m$

. The given equations then become:

v_{1} = v_{1} cos θ_{1} + v_{2} cos θ_{2}

and

0 = {v'}_{1} sin θ_{1} + {v'}_{2} sin θ_{2} .

Square each equation to get

\begin{array}{l} {v_{1}}^{2} & = & {v'}_{1}^{2} {cos}^{2} θ_{1} + {v'}_{2}^{2} {cos}^{2} θ_{2} + 2 {v'}_{1} {v'}_{2} cos θ_{1} cos θ_{2} \\ 0 & = & {v'}_{1}^{2} {sin}^{2} θ_{1} + {v'}_{2}^{2} {sin}^{2} θ_{2} + 2 {v'}_{1} {v'}_{2} sin θ_{1} sin θ_{2} . \end{array}

Add these two equations and simplify:

\begin{array}{l} {v_{1}}^{2} & = & {v'}_{1}^{2} + {v'}_{2}^{2} + 2 {v'}_{1} {v'}_{2} (cos θ_{1} cos θ_{2} + sin θ_{1} sin θ_{2}) \\ = & {v'}_{1}^{2} + {v'}_{2}^{2} + 2 {v'}_{1} {v'}_{2} [\frac{1}{2} cos (θ_{1} - θ_{2}) + \frac{1}{2} cos (θ_{1} + θ_{2}) + \frac{1}{2} cos (θ_{1} - θ_{2}) - \frac{1}{2} cos (θ_{1} + θ_{2})] \\ = & {v'}_{1}^{2} + {v'}_{2}^{2} + 2 {v'}_{1} {v'}_{2} cos (θ_{1} - θ_{2}) . \end{array}

Multiply the entire equation by $\frac{1}{2} m$

to recover the kinetic energy:

\frac{1}{2} {mv}_{1}^{2} = \frac{1}{2} m {v'}_{1}^{2} + \frac{1}{2} m {v'}_{2}^{2} + m {v'}_{1} {v'}_{2} cos (θ_{1} - θ_{2})

Integrated Concepts

A 90.0-kg ice hockey player hits a 0.150-kg puck, giving the puck a velocity of 45.0 m/s. If both are initially at rest and if the ice is frictionless, how far does the player recoil in the time it takes the puck to reach the goal 15.0 m away?

Glossary

point masses: structureless particles with no rotation or spin

This work is licensed under a Creative Commons Attribution 4.0 International License.

You can also download for free at http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@11.1

Attribution:

For questions regarding this license, please contact partners@openstaxcollege.org.
If you use this textbook as a bibliographic reference, then you should cite it as follows: OpenStax College, Physics. OpenStax CNX. http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@11.1.
If you redistribute this textbook in a print format, then you must include on every physical page the following attribution: "Download for free at http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@11.1."
If you redistribute part of this textbook, then you must retain in every digital format page view (including but not limited to EPUB, PDF, and HTML) and on every physical printed page the following attribution: "Download for free at http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@11.1."