Rotation Angle and Angular Velocity

In Kinematics, we studied motion along a straight line and introduced such concepts as displacement, velocity, and acceleration. Two-Dimensional Kinematics dealt with motion in two dimensions. Projectile motion is a special case of two-dimensional kinematics in which the object is projected into the air, while being subject to the gravitational force, and lands a distance away. In this chapter, we consider situations where the object does not land but moves in a curve. We begin the study of uniform circular motion by defining two angular quantities needed to describe rotational motion.

Rotation Angle

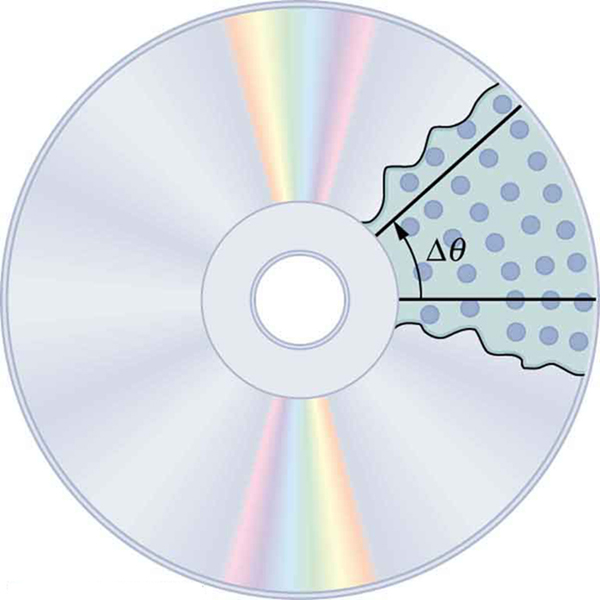
When objects rotate about some axis—for example, when the CD (compact disc) in [link] rotates about its center—each point in the object follows a circular arc. Consider a line from the center of the CD to its edge. Each pit used to record sound along this line moves through the same angle in the same amount of time. The rotation angle is the amount of rotation and is analogous to linear distance. We define the rotation angle $\text{Δ}\theta$

to be the ratio of the arc length to the radius of curvature:

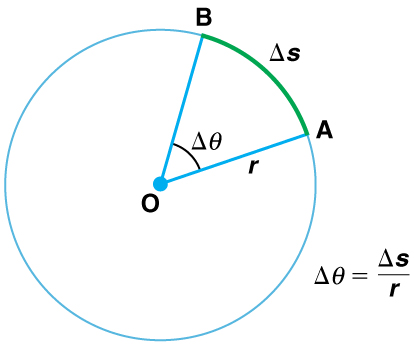
The arc length$\text{Δ}s$

is the distance traveled along a circular path as shown in [link] Note that $r$

is the radius of curvature of the circular path.

We know that for one complete revolution, the arc length is the circumference of a circle of radius $r$

. The circumference of a circle is $\mathrm{2\pi }r$

. Thus for one complete revolution the rotation angle is

This result is the basis for defining the units used to measure rotation angles, $\text{Δ}\theta$

to be radians (rad), defined so that

A comparison of some useful angles expressed in both degrees and radians is shown in [link].

If $\text{Δ}\theta =2\pi$

rad, then the CD has made one complete revolution, and every point on the CD is back at its original position. Because there are $\text{360º}$

in a circle or one revolution, the relationship between radians and degrees is thus

so that

Angular Velocity

How fast is an object rotating? We define angular velocity $\omega$

as the rate of change of an angle. In symbols, this is

where an angular rotation $\text{Δ}\theta$

takes place in a time $\text{Δ}t$

. The greater the rotation angle in a given amount of time, the greater the angular velocity. The units for angular velocity are radians per second (rad/s).

Angular velocity $\omega$

is analogous to linear velocity $v$

. To get the precise relationship between angular and linear velocity, we again consider a pit on the rotating CD. This pit moves an arc length $\text{Δ}s$

in a time $\text{Δ}t$

, and so it has a linear velocity

From $\text{Δ}\theta =\frac{\text{Δ}s}{r}$

we see that $\text{Δ}s=r\text{Δ}\theta$

. Substituting this into the expression for $v$

gives

We write this relationship in two different ways and gain two different insights:

The first relationship in $v=\mathrm{r\omega }\text{ or }\omega =\frac{v}{r}$

states that the linear velocity $v$

is proportional to the distance from the center of rotation, thus, it is largest for a point on the rim (largest $r$

), as you might expect. We can also call this linear speed $v$

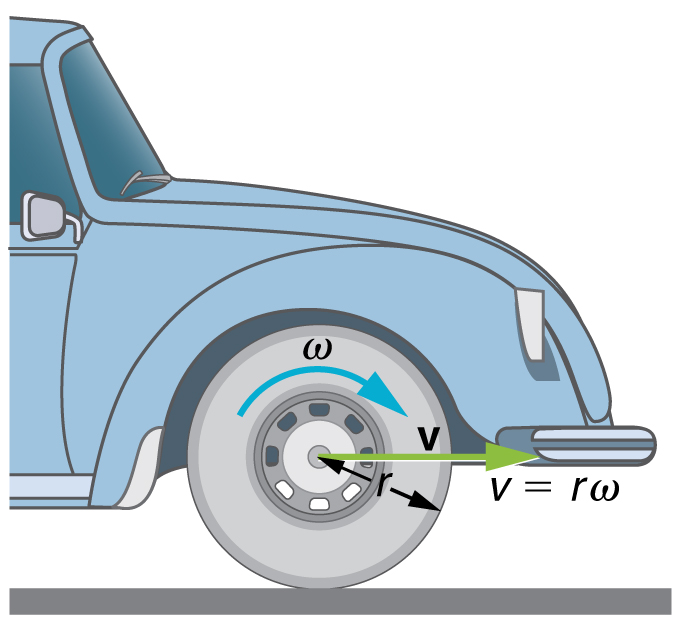
of a point on the rim the tangential speed. The second relationship in $v=\mathrm{r\omega }\text{ or }\omega =\frac{v}{r}$

can be illustrated by considering the tire of a moving car. Note that the speed of a point on the rim of the tire is the same as the speed $v$

of the car. See [link]. So the faster the car moves, the faster the tire spins—large $v$

means a large $\omega$

, because $v=\mathrm{r\omega }$

. Similarly, a larger-radius tire rotating at the same angular velocity ($\omega$

) will produce a greater linear speed ($v$

) for the car.

Both $\omega$

and $v$

have directions (hence they are angular and linear velocities, respectively). Angular velocity has only two directions with respect to the axis of rotation—it is either clockwise or counterclockwise. Linear velocity is tangent to the path, as illustrated in [link].

Section Summary

• Uniform circular motion is motion in a circle at constant speed. The rotation angle $\text{Δ}\theta$

  is defined as the ratio of the arc length to the radius of curvature:

  $\text{Δ}\theta =\frac{\text{Δ}s}{r}\text{,}$

  where arc length $\text{Δ}s$

  is distance traveled along a circular path and $r$

  is the radius of curvature of the circular path. The quantity $\text{Δ}\theta$

  is measured in units of radians (rad), for which

  $\mathrm{2\pi }\text{rad}=\text{360º}\text{= }1\text{ revolution.}$
• The conversion between radians and degrees is $1\text{rad}=\text{57}\text{.}3\text{º}$

  .

• Angular velocity $\omega$

  is the rate of change of an angle,

  $\omega =\frac{\text{Δ}\theta }{\text{Δ}t}\text{,}$

  where a rotation $\text{Δ}\theta$

  takes place in a time $\text{Δ}t$

  . The units of angular velocity are radians per second (rad/s). Linear velocity $v$

  and angular velocity $\omega$

  are related by

  $v=\mathrm{r\omega }\text{ or }\omega =\frac{v}{r}\text{.}$

Conceptual Questions

Problem Exercises

You can also download for free at http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@11.1

Attribution:

• For questions regarding this license, please contact partners@openstaxcollege.org.
• If you use this textbook as a bibliographic reference, then you should cite it as follows: OpenStax College, Physics. OpenStax CNX. http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@11.1.
• If you redistribute this textbook in a print format, then you must include on every physical page the following attribution: "Download for free at http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@11.1."
• If you redistribute part of this textbook, then you must retain in every digital format page view (including but not limited to EPUB, PDF, and HTML) and on every physical printed page the following attribution: "Download for free at http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@11.1."