Review of Pre-Calculus

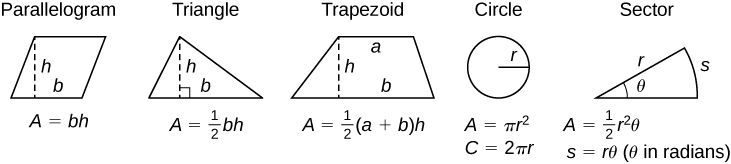
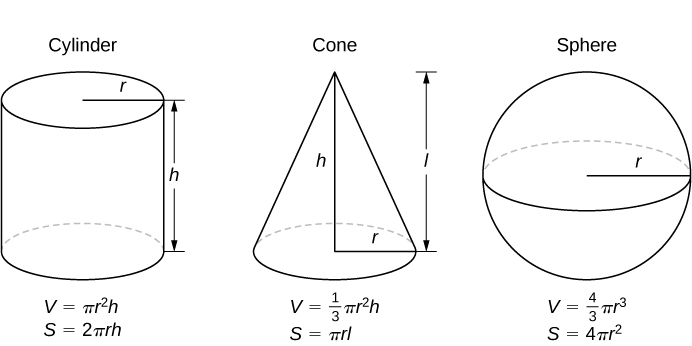Formulas from Geometry

A = area,

V = Volume, and

S = lateral surface area

### Formulas from Algebra

Laws of Exponents

\begin{matrix} x^{m} x^{n} & = & x^{m + n} & \frac{x^{m}}{x^{n}} & = & x^{m - n} & {(x^{m})}^{n} & = & x^{m n} \\ x^{− n} & = & \frac{1}{x^{n}} & {(x y)}^{n} & = & x^{n} y^{n} & {(\frac{x}{y})}^{n} & = & \frac{x^{n}}{y^{n}} \\ x^{1 / n} & = & \sqrt[n]{x} & \sqrt[n]{x y} & = & \sqrt[n]{x} \sqrt[n]{y} & \sqrt[n]{\frac{x}{y}} & = & \frac{\sqrt[n]{x}}{\sqrt[n]{y}} \\ x^{m / n} & = & \sqrt[n]{x^{m}} = {(\sqrt[n]{x})}^{m} \end{matrix}

Special Factorizations

\begin{matrix} x^{2} - y^{2} & = & (x + y) (x - y) \\ x^{3} + y^{3} & = & (x + y) (x^{2} - x y + y^{2}) \\ x^{3} - y^{3} & = & (x - y) (x^{2} + x y + y^{2}) \end{matrix}

Quadratic Formula

If $a x^{2} + b x + c = 0,$

then $x = \frac{− b \pm \sqrt{b^{2} - 4 c a}}{2 a} .$

Binomial Theorem

{(a + b)}^{n} = a^{n} + (\begin{array}{l} n \\ 1 \end{array}) a^{n - 1} b + (\begin{array}{l} n \\ 2 \end{array}) a^{n - 2} b^{2} + \dots + (\begin{matrix} n \\ n - 1 \end{matrix}) a b^{n - 1} + b^{n},

where $(\begin{array}{l} n \\ k \end{array}) = \frac{n (n - 1) (n - 2) \dots (n - k + 1)}{k (k - 1) (k - 2) \dots 3 \cdot 2 \cdot 1} = \frac{n!}{k! (n - k)!}$

Formulas from Trigonometry

Right-Angle Trigonometry

\begin{matrix} sin θ = \frac{opp}{hyp} & csc θ = \frac{hyp}{opp} \\ cos θ = \frac{adj}{hyp} & sec θ = \frac{hyp}{adj} \\ tan θ = \frac{opp}{adj} & cot θ = \frac{adj}{opp} \end{matrix}

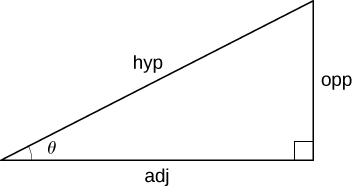The figure shows a right triangle with the longest side labeled hyp, the shorter leg labeled as opp, and the longer leg labeled as adj. The angle between the hypotenuse and the adjacent side is labeled theta. #### Trigonometric Functions of Important Angles

θ

Radians

sin θ

cos θ

tan θ


{: valign=”top”}	$0 °$

0

0

1

0

30 °

π / 6

1 / 2

\sqrt{3} / 2

\sqrt{3} / 3

45 °

π / 4

\sqrt{2} / 2

\sqrt{2} / 2

1

60 °

π / 3

\sqrt{3} / 2

1 / 2

\sqrt{3}

90 °

π / 2

1

0

—

Fundamental Identities

\begin{matrix} {sin}^{2} θ + {cos}^{2} θ & = & 1 & sin (− θ) & = & − sin θ \\ 1 + {tan}^{2} θ & = & {sec}^{2} θ & cos (− θ) & = & cos θ \\ 1 + {cot}^{2} θ & = & {csc}^{2} θ & tan (− θ) & = & − tan θ \\ sin (\frac{π}{2} - θ) & = & cos θ & sin (θ + 2 π) & = & sin θ \\ cos (\frac{π}{2} - θ) & = & sin θ & cos (θ + 2 π) & = & cos θ \\ tan (\frac{π}{2} - θ) & = & cot θ & tan (θ + π) & = & tan θ \end{matrix}

Law of Sines

\frac{sin A}{a} = \frac{sin B}{b} = \frac{sin C}{c}

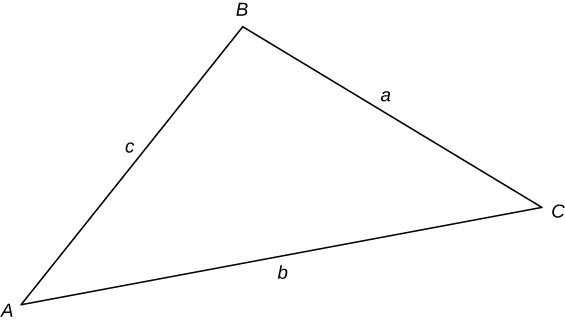The figure shows a nonright triangle with vertices labeled A, B, and C. The side opposite angle A is labeled a. The side opposite angle B is labeled b. The side opposite angle C is labeled c. #### Law of Cosines

\begin{matrix} a^{2} & = & b^{2} + c^{2} - 2 b c cos A \\ b^{2} & = & a^{2} + c^{2} - 2 a c cos B \\ c^{2} & = & a^{2} + b^{2} - 2 a b cos C \end{matrix}

Addition and Subtraction Formulas

\begin{matrix} sin (x + y) & = & sin x cos y + cos x sin y \\ sin (x - y) & = & sin x cos y - cos x sin y \\ cos (x + y) & = & cos x cos y - sin x sin y \\ cos (x - y) & = & cos x cos y + sin x sin y \\ tan (x + y) & = & \frac{tan x + tan y}{1 - tan x tan y} \\ tan (x - y) & = & \frac{tan x - tan y}{1 + tan x tan y} \end{matrix}

Double-Angle Formulas

\begin{matrix} sin 2 x & = & 2 sin x cos x \\ cos 2 x & = & {cos}^{2} x - {sin}^{2} x = 2 {cos}^{2} x - 1 = 1 - 2 {sin}^{2} x \\ tan 2 x & = & \frac{2 tan x}{1 - {tan}^{2} x} \end{matrix}

Half-Angle Formulas

\begin{matrix} {sin}^{2} x & = & \frac{1 - cos 2 x}{2} \\ {cos}^{2} x & = & \frac{1 + cos 2 x}{2} \end{matrix}

This work is licensed under a Creative Commons Attribution 4.0 International License.

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1

Attribution:

For questions regarding this license, please contact partners@openstaxcollege.org.
If you use this textbook as a bibliographic reference, then you should cite it as follows: OpenStax College, Calculus. OpenStax CNX. http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1.
If you redistribute this textbook in a print format, then you must include on every physical page the following attribution: "Download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1."
If you redistribute part of this textbook, then you must retain in every digital format page view (including but not limited to EPUB, PDF, and HTML) and on every physical printed page the following attribution: "Download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1."