We have examined several versions of the Fundamental Theorem of Calculus in higher dimensions that relate the integral around an oriented boundary of a domain to a “derivative” of that entity on the oriented domain. In this section, we state the divergence theorem, which is the final theorem of this type that we will study. The divergence theorem has many uses in physics; in particular, the divergence theorem is used in the field of partial differential equations to derive equations modeling heat flow and conservation of mass. We use the theorem to calculate flux integrals and apply it to electrostatic fields.
Before examining the divergence theorem, it is helpful to begin with an overview of the versions of the Fundamental Theorem of Calculus we have discussed:
This theorem relates the integral of derivative
over line segment
along the x-axis to a difference of
evaluated on the boundary.
where
is the initial point of C and
is the terminal point of C. The Fundamental Theorem for Line Integrals allows path C to be a path in a plane or in space, not just a line segment on the x-axis. If we think of the gradient as a derivative, then this theorem relates an integral of derivative
over path C to a difference of
evaluated on the boundary of C.
Since
and curl is a derivative of sorts, Green’s theorem relates the integral of derivative curlF over planar region D to an integral of F over the boundary of D.
Since
and divergence is a derivative of sorts, the flux form of Green’s theorem relates the integral of derivative divF over planar region D to an integral of F over the boundary of D.
If we think of the curl as a derivative of sorts, then Stokes’ theorem relates the integral of derivative curlF over surface S (not necessarily planar) to an integral of F over the boundary of S.
The divergence theorem follows the general pattern of these other theorems. If we think of divergence as a derivative of sorts, then the divergence theorem relates a triple integral of derivative divF over a solid to a flux integral of F over the boundary of the solid. More specifically, the divergence theorem relates a flux integral of vector field F over a closed surface S to a triple integral of the divergence of F over the solid enclosed by S.
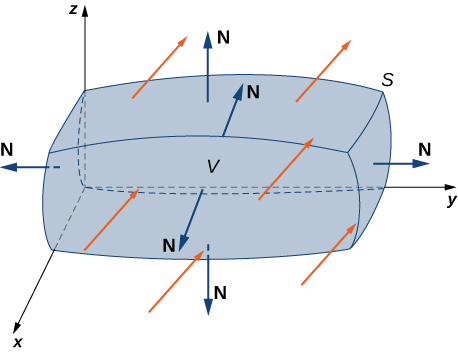
Let S be a piecewise, smooth closed surface that encloses solid E in space. Assume that S is oriented outward, and let F be a vector field with continuous partial derivatives on an open region containing E ([link]). Then

Recall that the flux form of Green’s theorem states that
Therefore, the divergence theorem is a version of Green’s theorem in one higher dimension.
The proof of the divergence theorem is beyond the scope of this text. However, we look at an informal proof that gives a general feel for why the theorem is true, but does not prove the theorem with full rigor. This explanation follows the informal explanation given for why Stokes’ theorem is true.
Let B be a small box with sides parallel to the coordinate planes inside E ([link]). Let the center of B have coordinates
and suppose the edge lengths are
and
([link](b)). The normal vector out of the top of the box is k and the normal vector out of the bottom of the box is
The dot product of
with k is R and the dot product with
is
The area of the top of the box (and the bottom of the box)
is
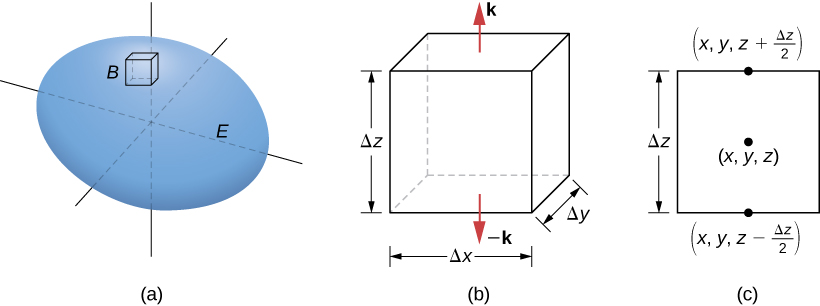
The flux out of the top of the box can be approximated by
([link](c)) and the flux out of the bottom of the box is
If we denote the difference between these values as
then the net flux in the vertical direction can be approximated by
However,
Therefore, the net flux in the vertical direction can be approximated by
Similarly, the net flux in the x-direction can be approximated by
and the net flux in the y-direction can be approximated by
Adding the fluxes in all three directions gives an approximation of the total flux out of the box:
This approximation becomes arbitrarily close to the value of the total flux as the volume of the box shrinks to zero.
The sum of
over all the small boxes approximating E is approximately
On the other hand, the sum of
over all the small boxes approximating E is the sum of the fluxes over all these boxes. Just as in the informal proof of Stokes’ theorem, adding these fluxes over all the boxes results in the cancelation of a lot of the terms. If an approximating box shares a face with another approximating box, then the flux over one face is the negative of the flux over the shared face of the adjacent box. These two integrals cancel out. When adding up all the fluxes, the only flux integrals that survive are the integrals over the faces approximating the boundary of E. As the volumes of the approximating boxes shrink to zero, this approximation becomes arbitrarily close to the flux over S.
□
Verify the divergence theorem for vector field
and surface S that consists of cone
and the circular top of the cone (see the following figure). Assume this surface is positively oriented.
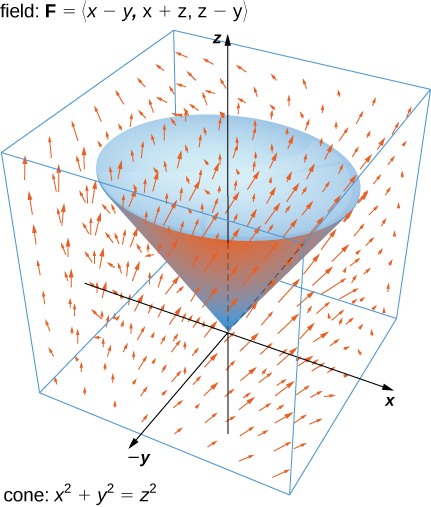
Let E be the solid cone enclosed by S. To verify the theorem for this example, we show that
by calculating each integral separately.
To compute the triple integral, note that
and therefore the triple integral is
The volume of a right circular cone is given by
In this case,
Therefore,
To compute the flux integral, first note that S is piecewise smooth; S can be written as a union of smooth surfaces. Therefore, we break the flux integral into two pieces: one flux integral across the circular top of the cone and one flux integral across the remaining portion of the cone. Call the circular top
and the portion under the top
We start by calculating the flux across the circular top of the cone. Notice that
has parameterization
Then, the tangent vectors are
and
Therefore, the flux across
is
We now calculate the flux over
A parameterization of this surface is
The tangent vectors are
and
so the cross product is
Notice that the negative signs on the x and y components induce the negative (or inward) orientation of the cone. Since the surface is positively oriented, we use vector
in the flux integral. The flux across
is then
The total flux across S is
and we have verified the divergence theorem for this example.
Verify the divergence theorem for vector field
and surface S given by the cylinder
plus the circular top and bottom of the cylinder. Assume that S is positively oriented.
Both integrals equal
Calculate both the flux integral and the triple integral with the divergence theorem and verify they are equal.
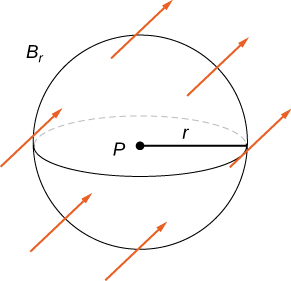
Recall that the divergence of continuous field F at point P is a measure of the “outflowing-ness” of the field at P. If F represents the velocity field of a fluid, then the divergence can be thought of as the rate per unit volume of the fluid flowing out less the rate per unit volume flowing in. The divergence theorem confirms this interpretation. To see this, let P be a point and let
be a ball of small radius r centered at P ([link]). Let
be the boundary sphere of
Since the radius is small and F is continuous,
for all other points Q in the ball. Therefore, the flux across
can be approximated using the divergence theorem:
Since
is a constant,
Therefore, flux
can be approximated by
This approximation gets better as the radius shrinks to zero, and therefore
This equation says that the divergence at P is the net rate of outward flux of the fluid per unit volume.
The divergence theorem translates between the flux integral of closed surface S and a triple integral over the solid enclosed by S. Therefore, the theorem allows us to compute flux integrals or triple integrals that would ordinarily be difficult to compute by translating the flux integral into a triple integral and vice versa.
Calculate the surface integral
where S is cylinder
including the circular top and bottom, and
We could calculate this integral without the divergence theorem, but the calculation is not straightforward because we would have to break the flux integral into three separate integrals: one for the top of the cylinder, one for the bottom, and one for the side. Furthermore, each integral would require parameterizing the corresponding surface, calculating tangent vectors and their cross product, and using [link].
By contrast, the divergence theorem allows us to calculate the single triple integral
where E is the solid enclosed by the cylinder. Using the divergence theorem and converting to cylindrical coordinates, we have
Use the divergence theorem to calculate flux integral
where S is the boundary of the box given by
and
(see the following figure).
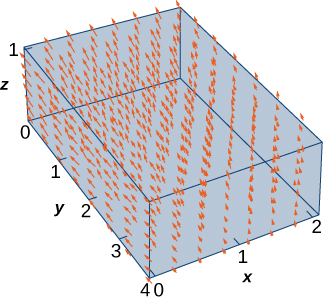
30
Calculate the corresponding triple integral.
Let
be the velocity field of a fluid. Let C be the solid cube given by
and let S be the boundary of this cube (see the following figure). Find the flow rate of the fluid across S.
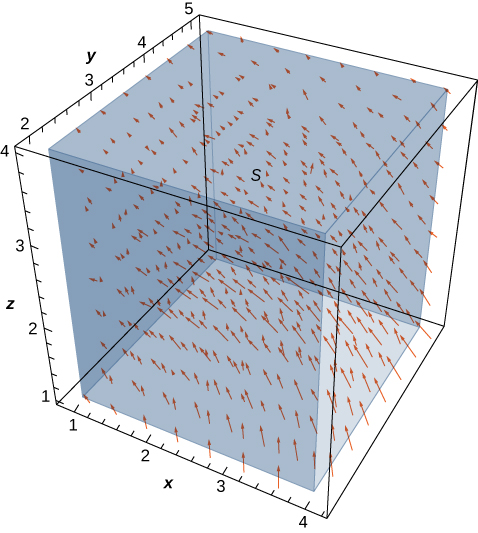
The flow rate of the fluid across S is
Before calculating this flux integral, let’s discuss what the value of the integral should be. Based on [link], we see that if we place this cube in the fluid (as long as the cube doesn’t encompass the origin), then the rate of fluid entering the cube is the same as the rate of fluid exiting the cube. The field is rotational in nature and, for a given circle parallel to the xy-plane that has a center on the z-axis, the vectors along that circle are all the same magnitude. That is how we can see that the flow rate is the same entering and exiting the cube. The flow into the cube cancels with the flow out of the cube, and therefore the flow rate of the fluid across the cube should be zero.
To verify this intuition, we need to calculate the flux integral. Calculating the flux integral directly requires breaking the flux integral into six separate flux integrals, one for each face of the cube. We also need to find tangent vectors, compute their cross product, and use [link]. However, using the divergence theorem makes this calculation go much more quickly:
Therefore the flux is zero, as expected.
Let
be the velocity field of a fluid. Let C be the solid cube given by
and let S be the boundary of this cube (see the following figure). Find the flow rate of the fluid across S.
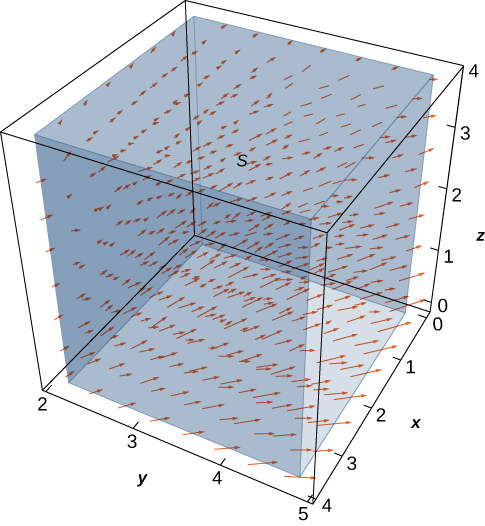
Use the divergence theorem and calculate a triple integral.
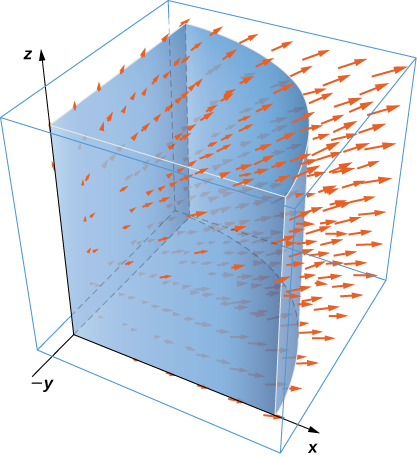
[link] illustrates a remarkable consequence of the divergence theorem. Let S be a piecewise, smooth closed surface and let F be a vector field defined on an open region containing the surface enclosed by S. If F has the form
then the divergence of F is zero. By the divergence theorem, the flux of F across S is also zero. This makes certain flux integrals incredibly easy to calculate. For example, suppose we wanted to calculate the flux integral
where S is a cube and
Calculating the flux integral directly would be difficult, if not impossible, using techniques we studied previously. At the very least, we would have to break the flux integral into six integrals, one for each face of the cube. But, because the divergence of this field is zero, the divergence theorem immediately shows that the flux integral is zero.
We can now use the divergence theorem to justify the physical interpretation of divergence that we discussed earlier. Recall that if F is a continuous three-dimensional vector field and P is a point in the domain of F, then the divergence of F at P is a measure of the “outflowing-ness” of F at P. If F represents the velocity field of a fluid, then the divergence of F at P is a measure of the net flow rate out of point P (the flow of fluid out of P less the flow of fluid in to P). To see how the divergence theorem justifies this interpretation, let
be a ball of very small radius r with center P, and assume that
is in the domain of F. Furthermore, assume that
has a positive, outward orientation. Since the radius of
is small and F is continuous, the divergence of F is approximately constant on
That is, if
is any point in
then
Let
denote the boundary sphere of
We can approximate the flux across
using the divergence theorem as follows:
As we shrink the radius r to zero via a limit, the quantity
gets arbitrarily close to the flux. Therefore,
and we can consider the divergence at P as measuring the net rate of outward flux per unit volume at P. Since “outflowing-ness” is an informal term for the net rate of outward flux per unit volume, we have justified the physical interpretation of divergence we discussed earlier, and we have used the divergence theorem to give this justification.
The divergence theorem has many applications in physics and engineering. It allows us to write many physical laws in both an integral form and a differential form (in much the same way that Stokes’ theorem allowed us to translate between an integral and differential form of Faraday’s law). Areas of study such as fluid dynamics, electromagnetism, and quantum mechanics have equations that describe the conservation of mass, momentum, or energy, and the divergence theorem allows us to give these equations in both integral and differential forms.
One of the most common applications of the divergence theorem is to electrostatic fields. An important result in this subject is Gauss’ law. This law states that if S is a closed surface in electrostatic field E, then the flux of E across S is the total charge enclosed by S (divided by an electric constant). We now use the divergence theorem to justify the special case of this law in which the electrostatic field is generated by a stationary point charge at the origin.
If
is a point in space, then the distance from the point to the origin is
Let
denote radial vector field
The vector at a given position in space points in the direction of unit radial vector
and is scaled by the quantity
Therefore, the magnitude of a vector at a given point is inversely proportional to the square of the vector’s distance from the origin. Suppose we have a stationary charge of q Coulombs at the origin, existing in a vacuum. The charge generates electrostatic field E given by
where the approximation
farad (F)/m is an electric constant. (The constant
is a measure of the resistance encountered when forming an electric field in a vacuum.) Notice that E is a radial vector field similar to the gravitational field described in [link]. The difference is that this field points outward whereas the gravitational field points inward. Because
we say that electrostatic fields obey an inverse-square law. That is, the electrostatic force at a given point is inversely proportional to the square of the distance from the source of the charge (which in this case is at the origin). Given this vector field, we show that the flux across closed surface S is zero if the charge is outside of S, and that the flux is
if the charge is inside of S. In other words, the flux across S is the charge inside the surface divided by constant
This is a special case of Gauss’ law, and here we use the divergence theorem to justify this special case.
To show that the flux across S is the charge inside the surface divided by constant
we need two intermediate steps. First we show that the divergence of
is zero and then we show that the flux of
across any smooth surface S is either zero or
We can then justify this special case of Gauss’ law.
Verify that the divergence of
is zero where
is defined (away from the origin).
Since
the quotient rule gives us
Similarly,
Therefore,
Notice that since the divergence of
is zero and E is
scaled by a constant, the divergence of electrostatic field E is also zero (except at the origin).
Let S be a connected, piecewise smooth closed surface and let
Then,
In other words, this theorem says that the flux of
across any piecewise smooth closed surface S depends only on whether the origin is inside of S.
The logic of this proof follows the logic of [link], only we use the divergence theorem rather than Green’s theorem.
First, suppose that S does not encompass the origin. In this case, the solid enclosed by S is in the domain of
and since the divergence of
is zero, we can immediately apply the divergence theorem and find that
is zero.
Now suppose that S does encompass the origin. We cannot just use the divergence theorem to calculate the flux, because the field is not defined at the origin. Let
be a sphere of radius a inside of S centered at the origin. The outward normal vector field on the sphere, in spherical coordinates, is
(see [link]). Therefore, on the surface of the sphere, the dot product
(in spherical coordinates) is
The flux of
across
is
Now, remember that we are interested in the flux across S, not necessarily the flux across
To calculate the flux across S, let E be the solid between surfaces
and S. Then, the boundary of E consists of
and S. Denote this boundary by
to indicate that S is oriented outward but now
is oriented inward. We would like to apply the divergence theorem to solid E. Notice that the divergence theorem, as stated, can’t handle a solid such as E because E has a hole. However, the divergence theorem can be extended to handle solids with holes, just as Green’s theorem can be extended to handle regions with holes. This allows us to use the divergence theorem in the following way. By the divergence theorem,
Therefore,
and we have our desired result.
□
Now we return to calculating the flux across a smooth surface in the context of electrostatic field
of a point charge at the origin. Let S be a piecewise smooth closed surface that encompasses the origin. Then
If S does not encompass the origin, then
Therefore, we have justified the claim that we set out to justify: the flux across closed surface S is zero if the charge is outside of S, and the flux is
if the charge is inside of S.
This analysis works only if there is a single point charge at the origin. In this case, Gauss’ law says that the flux of E across S is the total charge enclosed by S. Gauss’ law can be extended to handle multiple charged solids in space, not just a single point charge at the origin. The logic is similar to the previous analysis, but beyond the scope of this text. In full generality, Gauss’ law states that if S is a piecewise smooth closed surface and Q is the total amount of charge inside of S, then the flux of E across S is
Suppose we have four stationary point charges in space, all with a charge of 0.002 Coulombs (C). The charges are located at
Let E denote the electrostatic field generated by these point charges. If S is the sphere of radius 2 oriented outward and centered at the origin, then find
According to Gauss’ law, the flux of E across S is the total charge inside of S divided by the electric constant. Since S has radius 2, notice that only two of the charges are inside of S: the charge at
and the charge at
Therefore, the total charge encompassed by S is 0.004 and, by Gauss’ law,
Work the previous example for surface S that is a sphere of radius 4 centered at the origin, oriented outward.
Use Gauss’ law.
For the following exercises, use a computer algebraic system (CAS) and the divergence theorem to evaluate surface integral
for the given choice of F and the boundary surface S. For each closed surface, assume N is the outward unit normal vector.
[T]
S is the surface of cube
[T]
S is the surface of hemisphere
together with disk
in the xy-plane.
[T]
S is the surface of the five faces of unit cube
[T]
S is the surface of paraboloid
[T]
S is the surface of sphere
[T]
S is the surface of the solid bounded by cylinder
and planes
[T]
S is the surface bounded above by sphere
and below by cone
in spherical coordinates. (Think of S as the surface of an “ice cream cone.”)
[T]
S is the surface bounded by cylinder
and planes
[T] Surface integral
where S is the solid bounded by paraboloid
and plane
and
Use the divergence theorem to calculate surface integral
where
and S is upper hemisphere
oriented upward.
Use the divergence theorem to calculate surface integral
where
and S is the surface bounded by cylinder
and planes
and
Use the divergence theorem to calculate surface integral
when
and S is the surface of the box with vertices
Use the divergence theorem to calculate surface integral
when
and S is a part of paraboloid
that lies above plane
and is oriented upward.
[T] Use a CAS and the divergence theorem to calculate flux
where
and S is a sphere with center (0, 0) and radius 2.
Use the divergence theorem to compute the value of flux integral
where
and S is the area of the region bounded by
Use the divergence theorem to compute flux integral
where
and S consists of the union of paraboloid
and disk
oriented outward. What is the flux through just the paraboloid?
Use the divergence theorem to compute flux integral
where
and S is a part of cone
beneath top plane
oriented downward.
Use the divergence theorem to calculate surface integral
for
where S is the surface bounded by cylinder
and planes
Consider
Let E be the solid enclosed by paraboloid
and plane
with normal vectors pointing outside E. Compute flux F across the boundary of E using the divergence theorem.
For the following exercises, use a CAS along with the divergence theorem to compute the net outward flux for the fields across the given surfaces S.
[T]
S is sphere
[T]
S is the boundary of the tetrahedron in the first octant formed by plane
[T]
S is sphere
[T]
S is the surface of paraboloid
for
plus its base in the xy-plane.
For the following exercises, use a CAS and the divergence theorem to compute the net outward flux for the vector fields across the boundary of the given regions D.
[T]
D is the region between spheres of radius 2 and 4 centered at the origin.
[T]
D is the region between spheres of radius 1 and 2 centered at the origin.
[T]
D is the region in the first octant between planes
and
20
Let
Use the divergence theorem to calculate
where S is the surface of the cube with corners at
oriented outward.
Use the divergence theorem to find the outward flux of field
through the cube bounded by planes
Let
and let S be hemisphere
together with disk
in the xy-plane. Use the divergence theorem.
Evaluate
where
and S is the surface consisting of all faces except the tetrahedron bounded by plane
and the coordinate planes, with outward unit normal vector N.
Find the net outward flux of field
across any smooth closed surface in
where a, b, and c are constants.
Use the divergence theorem to evaluate
where
and S is sphere
with constant
Use the divergence theorem to evaluate
where
and S is the boundary of the cube defined by
Let R be the region defined by
Use the divergence theorem to find
Let E be the solid bounded by the xy-plane and paraboloid
so that S is the surface of the paraboloid piece together with the disk in the xy-plane that forms its bottom. If
find
using the divergence theorem.
Let E be the solid unit cube with diagonally opposite corners at the origin and (1, 1, 1), and faces parallel to the coordinate planes. Let S be the surface of E, oriented with the outward-pointing normal. Use a CAS to find
using the divergence theorem if
Use the divergence theorem to calculate the flux of
through sphere
Find
where
and S is the outwardly oriented surface obtained by removing cube
from cube
Consider radial vector field
Compute the surface integral, where S is the surface of a sphere of radius a centered at the origin.
Compute the flux of water through parabolic cylinder
from
if the velocity vector is
[T] Use a CAS to find the flux of vector field
across the portion of hyperboloid
between planes
and
oriented so the unit normal vector points away from the z-axis.
[T] Use a CAS to find the flux of vector field
through surface S, where S is given by
from
oriented so the unit normal vector points downward.
[T] Use a CAS to compute
where
and S is a part of sphere
with
Evaluate
where
and S is a closed surface bounding the region and consisting of solid cylinder
and
[T] Use a CAS to calculate the flux of
across surface S, where S is the boundary of the solid bounded by hemispheres
and
and plane
Use the divergence theorem to evaluate
where
and S is the surface consisting of three pieces:
on the top;
on the sides; and
on the bottom.
[T] Use a CAS and the divergence theorem to evaluate
where
and S is sphere
orientated outward.
Use the divergence theorem to evaluate
where
and S is the boundary of the solid enclosed by paraboloid
cylinder
and plane
and S is oriented outward.
For the following exercises, Fourier’s law of heat transfer states that the heat flow vector F at a point is proportional to the negative gradient of the temperature; that is,
which means that heat energy flows hot regions to cold regions. The constant
is called the conductivity, which has metric units of joules per meter per second-kelvin or watts per meter-kelvin. A temperature function for region D is given. Use the divergence theorem to find net outward heat flux
across the boundary S of D, where
D is the sphere of radius a centered at the origin.
True or False? Justify your answer with a proof or a counterexample.
Vector field
is conservative.
False
For vector field
if
in open region
then
The divergence of a vector field is a vector field.
False
If
then
is a conservative vector field.
Draw the following vector fields.
Are the following the vector fields conservative? If so, find the potential function
such that
Conservative,
Conservative,
Evaluate the following integrals.
along
from (0, 0) to (4, 2)
where
where S is surface
Find the divergence and curl for the following vector fields.
Divergence:
curl:
Use Green’s theorem to evaluate the following integrals.
where C is a square with vertices (0, 0), (0, 2), (2, 2) and (2, 0)
where C is a circle centered at the origin with radius 3
Use Stokes’ theorem to evaluate
where
is the upper half of the unit sphere
where
is the upward-facing paraboloid
lying in cylinder
Use the divergence theorem to evaluate
over cube
defined by
where
is bounded by paraboloid
and plane
Find the amount of work performed by a 50-kg woman ascending a helical staircase with radius 2 m and height 100 m. The woman completes five revolutions during the climb.
Find the total mass of a thin wire in the shape of a semicircle with radius
and a density function of
Find the total mass of a thin sheet in the shape of a hemisphere with radius 2 for
with a density function
Use the divergence theorem to compute the value of the flux integral over the unit sphere with

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: