We have already discussed a few applications of multiple integrals, such as finding areas, volumes, and the average value of a function over a bounded region. In this section we develop computational techniques for finding the center of mass and moments of inertia of several types of physical objects, using double integrals for a lamina (flat plate) and triple integrals for a three-dimensional object with variable density. The density is usually considered to be a constant number when the lamina or the object is homogeneous; that is, the object has uniform density.
The center of mass is also known as the center of gravity if the object is in a uniform gravitational field. If the object has uniform density, the center of mass is the geometric center of the object, which is called the centroid. [link] shows a point
as the center of mass of a lamina. The lamina is perfectly balanced about its center of mass.

To find the coordinates of the center of mass
of a lamina, we need to find the moment
of the lamina about the
and the moment
about the
We also need to find the mass
of the lamina. Then
Refer to Moments and Centers of Mass for the definitions and the methods of single integration to find the center of mass of a one-dimensional object (for example, a thin rod). We are going to use a similar idea here except that the object is a two-dimensional lamina and we use a double integral.
If we allow a constant density function, then
give the centroid of the lamina.
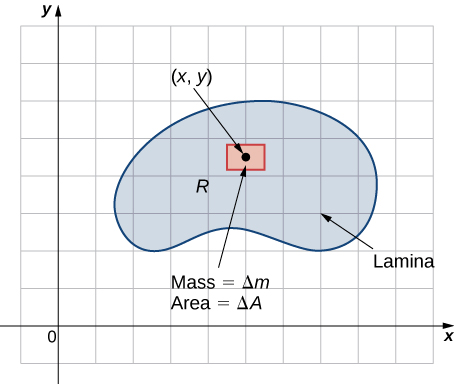
Suppose that the lamina occupies a region
in the
and let
be its density (in units of mass per unit area) at any point
Hence,
where
and
are the mass and area of a small rectangle containing the point
and the limit is taken as the dimensions of the rectangle go to
(see the following figure).
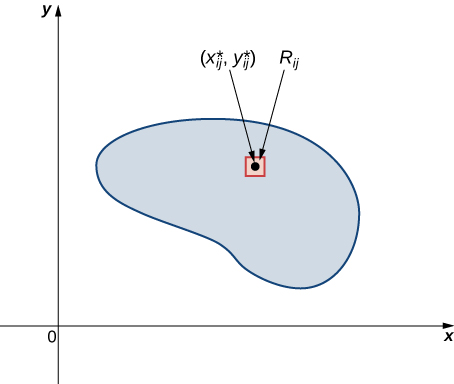
Just as before, we divide the region
into tiny rectangles
with area
and choose
as sample points. Then the mass
of each
is equal to
([link]). Let
and
be the number of subintervals in
and
respectively. Also, note that the shape might not always be rectangular but the limit works anyway, as seen in previous sections.
Hence, the mass of the lamina is
Let’s see an example now of finding the total mass of a triangular lamina.
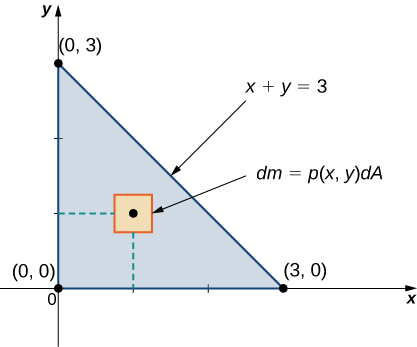
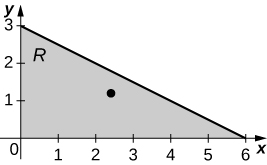
Consider a triangular lamina
with vertices
and with density
Find the total mass.
A sketch of the region
is always helpful, as shown in the following figure.
Using the expression developed for mass, we see that
The computation is straightforward, giving the answer
Consider the same region
as in the previous example, and use the density function
Find the total mass.
Now that we have established the expression for mass, we have the tools we need for calculating moments and centers of mass. The moment
about the
for
is the limit of the sums of moments of the regions
about the
Hence
Similarly, the moment
about the
for
is the limit of the sums of moments of the regions
about the
Hence
Consider the same triangular lamina
with vertices
and with density
Find the moments
and
Use double integrals for each moment and compute their values:
The computation is quite straightforward.
Consider the same lamina
as above, and use the density function
Find the moments
and
and
Finally we are ready to restate the expressions for the center of mass in terms of integrals. We denote the x-coordinate of the center of mass by
and the y-coordinate by
Specifically,
Again consider the same triangular region
with vertices
and with density function
Find the center of mass.
Using the formulas we developed, we have
Therefore, the center of mass is the point
If we choose the density
instead to be uniform throughout the region (i.e., constant), such as the value 1 (any constant will do), then we can compute the centroid,
Notice that the center of mass
is not exactly the same as the centroid
of the triangular region. This is due to the variable density of
If the density is constant, then we just use
(constant). This value cancels out from the formulas, so for a constant density, the center of mass coincides with the centroid of the lamina.
Again use the same region
as above and the density function
Find the center of mass.
and
Once again, based on the comments at the end of [link], we have expressions for the centroid of a region on the plane:
We should use these formulas and verify the centroid of the triangular region
referred to in the last three examples.
Find the mass, moments, and the center of mass of the lamina of density
occupying the region
under the curve
in the interval
(see the following figure).
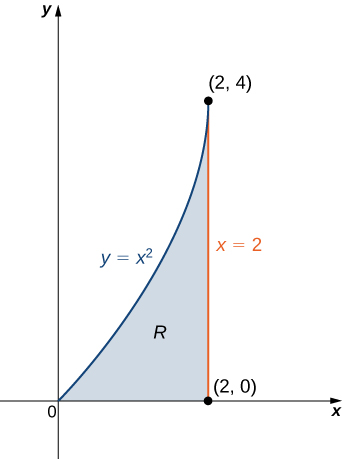
First we compute the mass
We need to describe the region between the graph of
and the vertical lines
and
Now compute the moments
and
Finally, evaluate the center of mass,
Hence the center of mass is
Calculate the mass, moments, and the center of mass of the region between the curves
and
with the density function
in the interval
and
Find the centroid of the region under the curve
over the interval
(see the following figure).
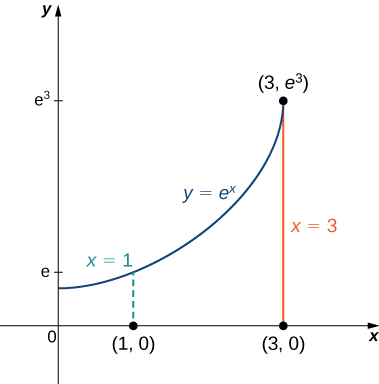
To compute the centroid, we assume that the density function is constant and hence it cancels out:
Thus the centroid of the region is
Calculate the centroid of the region between the curves
and
with uniform density in the interval
For a clear understanding of how to calculate moments of inertia using double integrals, we need to go back to the general definition in Section
The moment of inertia of a particle of mass
about an axis is
where
is the distance of the particle from the axis. We can see from [link] that the moment of inertia of the subrectangle
about the
is
Similarly, the moment of inertia of the subrectangle
about the
is
The moment of inertia is related to the rotation of the mass; specifically, it measures the tendency of the mass to resist a change in rotational motion about an axis.
The moment of inertia
about the
for the region
is the limit of the sum of moments of inertia of the regions
about the
Hence
Similarly, the moment of inertia
about the
for
is the limit of the sum of moments of inertia of the regions
about the
Hence
Sometimes, we need to find the moment of inertia of an object about the origin, which is known as the polar moment of inertia. We denote this by
and obtain it by adding the moments of inertia
and
Hence
All these expressions can be written in polar coordinates by substituting
and
For example,
Use the triangular region
with vertices
and
and with density
as in previous examples. Find the moments of inertia.
Using the expressions established above for the moments of inertia, we have
Again use the same region
as above and the density function
Find the moments of inertia.
and
Also,
As mentioned earlier, the moment of inertia of a particle of mass
about an axis is
where
is the distance of the particle from the axis, also known as the radius of gyration.
Hence the radii of gyration with respect to the
the
and the origin are
respectively. In each case, the radius of gyration tells us how far (perpendicular distance) from the axis of rotation the entire mass of an object might be concentrated. The moments of an object are useful for finding information on the balance and torque of the object about an axis, but radii of gyration are used to describe the distribution of mass around its centroidal axis. There are many applications in engineering and physics. Sometimes it is necessary to find the radius of gyration, as in the next example.
Consider the same triangular lamina
with vertices
and
and with density
as in previous examples. Find the radii of gyration with respect to the
the
and the origin.
If we compute the mass of this region we find that
We found the moments of inertia of this lamina in [link]. From these data, the radii of gyration with respect to the
and the origin are, respectively,
Use the same region
from [link] and the density function
Find the radii of gyration with respect to the
the
and the origin.
and
Follow the steps shown in the previous example.
All the expressions of double integrals discussed so far can be modified to become triple integrals.
If we have a solid object
with a density function
at any point
in space, then its mass is
Its moments about the
the
and the
are
If the center of mass of the object is the point
then
Also, if the solid object is homogeneous (with constant density), then the center of mass becomes the centroid of the solid. Finally, the moments of inertia about the
the
and the
are
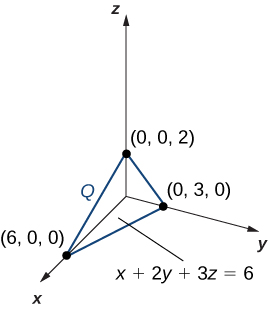
Suppose that
is a solid region bounded by
and the coordinate planes and has density
Find the total mass.
The region
is a tetrahedron ([link]) meeting the axes at the points
and
To find the limits of integration, let
in the slanted plane
Then for
and
find the projection of
onto the
which is bounded by the axes and the line
Hence the mass is
Follow the steps in the previous example.
Suppose
is a solid region bounded by the plane
and the coordinate planes with density
(see [link]). Find the center of mass using decimal approximation.
We have used this tetrahedron before and know the limits of integration, so we can proceed to the computations right away. First, we need to find the moments about the
the
and the
Hence the center of mass is
The center of mass for the tetrahedron
is the point
Check that
and
Then use
from a previous checkpoint question.
We conclude this section with an example of finding moments of inertia
and
Suppose that
is a solid region and is bounded by
and the coordinate planes with density
(see [link]). Find the moments of inertia of the tetrahedron
about the
the
and the
Once again, we can almost immediately write the limits of integration and hence we can quickly proceed to evaluating the moments of inertia. Using the formula stated before, the moments of inertia of the tetrahedron
about the
the
and the
are
and
Proceeding with the computations, we have
Thus, the moments of inertia of the tetrahedron
about the
the
and the
are
respectively.
Consider the same region
([link]), and use the density function
Find the moments of inertia about the three coordinate planes.
The moments of inertia of the tetrahedron
about the
the
and the
are
respectively.
Finding the mass, center of mass, moments, and moments of inertia in double integrals:
with a density function
at any point
in the plane, the mass is
and
are
and the origin are
Finding the mass, center of mass, moments, and moments of inertia in triple integrals:
with a density function
at any point
in space, the mass is
the
and the
are
the
and the
are
and
In the following exercises, the region
occupied by a lamina is shown in a graph. Find the mass of
with the density function
is the triangular region with vertices
and
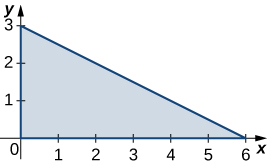
is the triangular region with vertices
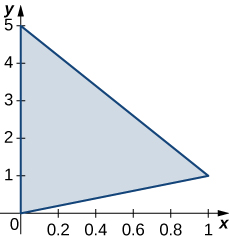
is the rectangular region with vertices
and
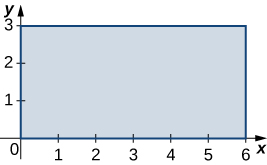
is the rectangular region with vertices
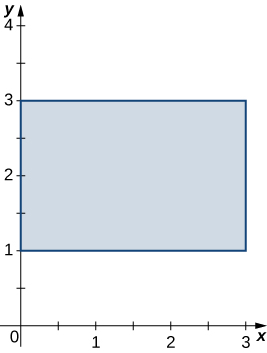
and
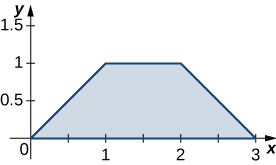
is the trapezoidal region determined by the lines
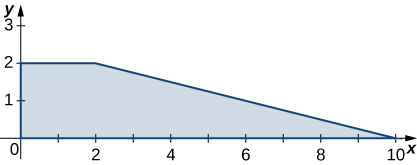
and
is the trapezoidal region determined by the lines
and
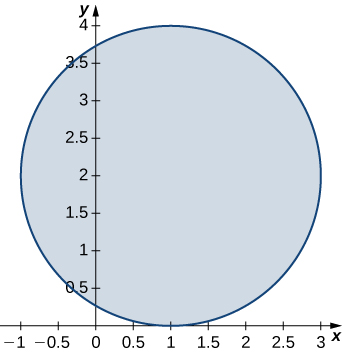
is the disk of radius
centered at
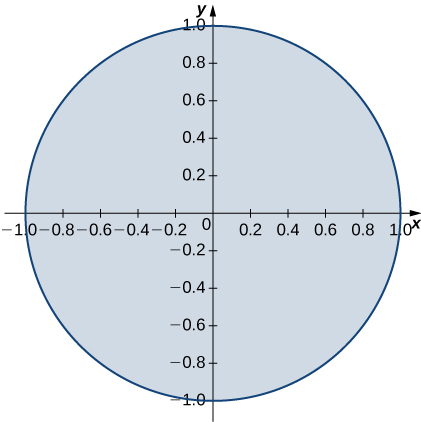
is the unit disk;
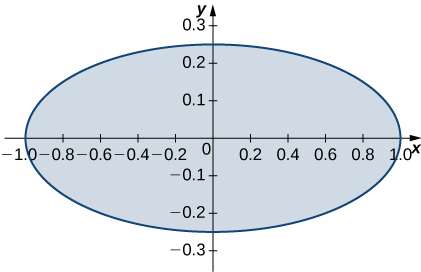
is the region enclosed by the ellipse
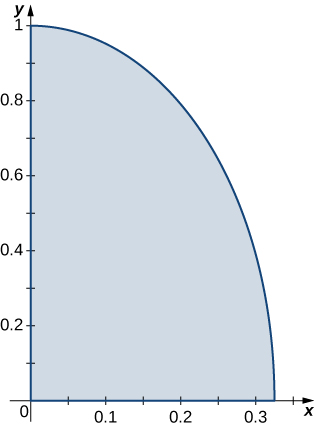
is the region bounded by
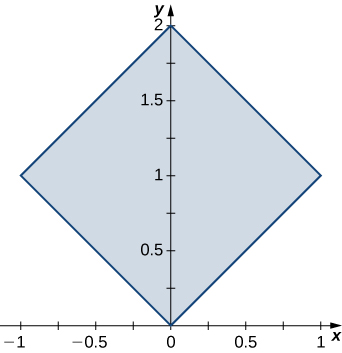
is the region bounded by
and
In the following exercises, consider a lamina occupying the region
and having the density function
given in the preceding group of exercises. Use a computer algebra system (CAS) to answer the following questions.
and
about the
and
respectively.
[T]
is the triangular region with vertices
and
a.
b.
c.* * *
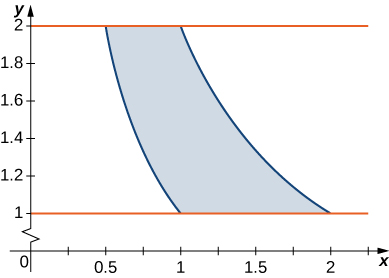
[T]
is the triangular region with vertices
[T]
is the rectangular region with vertices
a.
b.
c.* * *
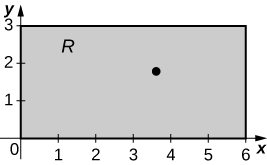
[T]
is the rectangular region with vertices
[T]
is the trapezoidal region determined by the lines
a.
b.
c.* * *
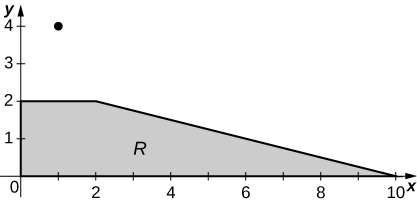
[T]
is the trapezoidal region determined by the lines
and
[T]
is the disk of radius
centered at
a.
b.
c.* * *
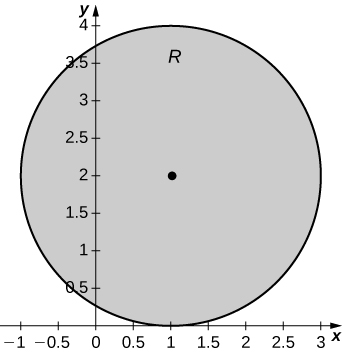
[T]
is the unit disk;
[T]
is the region enclosed by the ellipse
a.
b.
c.* * *
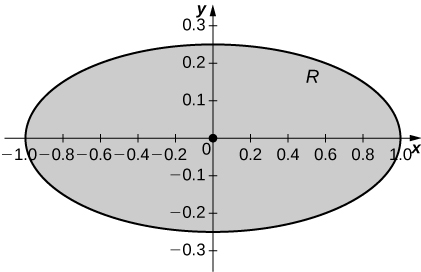
[T]
[T]
is the region bounded by
and
a.
b.
c.* * *
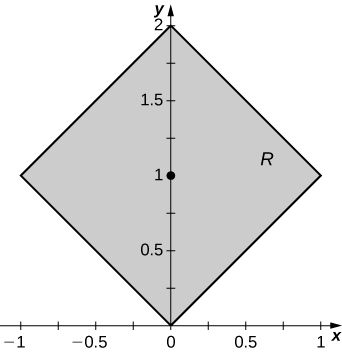
[T]
is the region bounded by
In the following exercises, consider a lamina occupying the region
and having the density function
given in the first two groups of Exercises.
and
about the
and origin, respectively.
and origin, respectively.
is the triangular region with vertices
and
a.
b.
is the triangular region with vertices
and
is the rectangular region with vertices
and
a.
b.
is the rectangular region with vertices
and
is the trapezoidal region determined by the lines
and
a.
b.
and
is the trapezoidal region determined by the lines
and
is the disk of radius
centered at
a.
b.
and
is the unit disk;
is the region enclosed by the ellipse
a.
b.
is the region bounded by
a.
b.
is the region bounded by
Let
be the solid unit cube. Find the mass of the solid if its density
is equal to the square of the distance of an arbitrary point of
to the
Let
be the solid unit hemisphere. Find the mass of the solid if its density
is proportional to the distance of an arbitrary point of
to the origin.
The solid
of constant density
is situated inside the sphere
and outside the sphere
Show that the center of mass of the solid is not located within the solid.
Find the mass of the solid
whose density is
where
[T] The solid
has density equal to the distance to the
Use a CAS to answer the following questions.
about the
and
respectively.
and locate its center of mass.
a.
b.
c.
d. the solid
and its center of mass are shown in the following figure.* * *
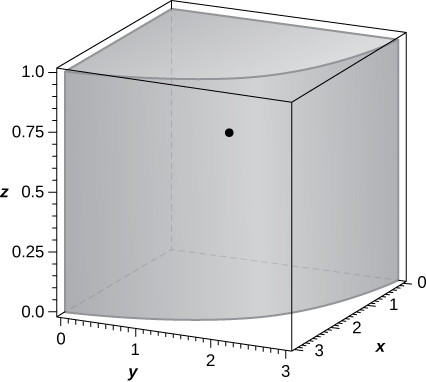
Consider the solid
with the density function
about the
and
respectively.
[T] The solid
has the mass given by the triple integral
Use a CAS to answer the following questions.
is located in the
and locate its center of mass.
a.
b. the solid
and its center of mass are shown in the following figure.* * *
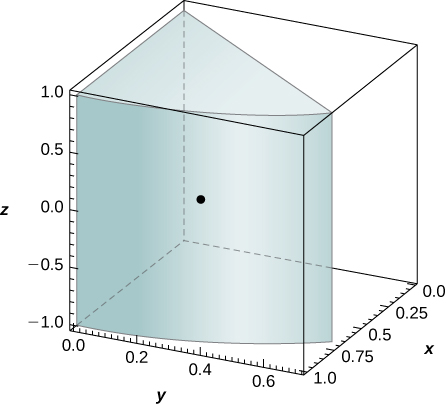
The solid
is bounded by the planes
Its density at any point is equal to the distance to the
Find the moments of inertia
of the solid about the
The solid
is bounded by the planes
and
Its density is
where
Show that the center of mass of the solid is located in the plane
for any value of
Let
be the solid situated outside the sphere
and inside the upper hemisphere
where
If the density of the solid is
find
such that the mass of the solid is
The mass of a solid
is given by
where
is an integer. Determine
such the mass of the solid is
Let
be the solid bounded above the cone
and below the sphere
Its density is a constant
Find
such that the center of mass of the solid is situated
units from the origin.
The solid
has the density
Show that the moment
about the
is half of the moment
about the
The solid
is bounded by the cylinder
the paraboloid
and the
where
Find the mass of the solid if its density is given by
Let
be a solid of constant density
where
that is located in the first octant, inside the circular cone
and above the plane
Show that the moment
about the
is the same as the moment
about the
The solid
has the mass given by the triple integral
about the
The solid
has the moment of inertia
about the
given by the triple integral
about the
a.
b.
The solid
has the mass given by the triple integral
about the
Let
be the solid bounded by the
the cylinder
and the plane
where
is a real number. Find the moment
of the solid about the
if its density given in cylindrical coordinates is
where
is a differentiable function with the first and second derivatives continuous and differentiable on
A solid
has a volume given by
where
is the projection of the solid onto the
and
are real numbers, and its density does not depend on the variable
Show that its center of mass lies in the plane
Consider the solid enclosed by the cylinder
and the planes
and
where
and
are real numbers. The density of
is given by
where
is a differential function whose derivative is continuous on
Show that if
then the moment of inertia about the
of
is null.
[T] The average density of a solid
is defined as
where
and
are the volume and the mass of
respectively. If the density of the unit ball centered at the origin is
use a CAS to find its average density. Round your answer to three decimal places.
Show that the moments of inertia
about the
and
respectively, of the unit ball centered at the origin whose density is
are the same. Round your answer to two decimal places.

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: