Earlier in this chapter we showed how to convert a double integral in rectangular coordinates into a double integral in polar coordinates in order to deal more conveniently with problems involving circular symmetry. A similar situation occurs with triple integrals, but here we need to distinguish between cylindrical symmetry and spherical symmetry. In this section we convert triple integrals in rectangular coordinates into a triple integral in either cylindrical or spherical coordinates.
Also recall the chapter opener, which showed the opera house l’Hemisphèric in Valencia, Spain. It has four sections with one of the sections being a theater in a five-story-high sphere (ball) under an oval roof as long as a football field. Inside is an IMAX screen that changes the sphere into a planetarium with a sky full of
twinkling stars. Using triple integrals in spherical coordinates, we can find the volumes of different geometric shapes like these.
As we have seen earlier, in two-dimensional space
a point with rectangular coordinates
can be identified with
in polar coordinates and vice versa, where
and
are the relationships between the variables.
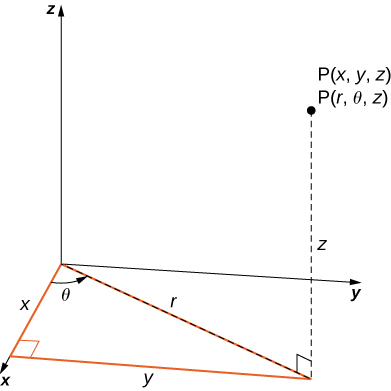
In three-dimensional space
a point with rectangular coordinates
can be identified with cylindrical coordinates
and vice versa. We can use these same conversion relationships, adding
as the vertical distance to the point from the
-plane as shown in the following figure.

To convert from rectangular to cylindrical coordinates, we use the conversion
and
To convert from cylindrical to rectangular coordinates, we use
and
The
-coordinate remains the same in both cases.
In the two-dimensional plane with a rectangular coordinate system, when we say
(constant) we mean an unbounded vertical line parallel to the
-axis and when
(constant) we mean an unbounded horizontal line parallel to the
-axis. With the polar coordinate system, when we say
(constant), we mean a circle of radius
units and when
(constant) we mean an infinite ray making an angle
with the positive
-axis.
Similarly, in three-dimensional space with rectangular coordinates
the equations
and
where
and
are constants, represent unbounded planes parallel to the
-plane,
-plane and
-plane, respectively. With cylindrical coordinates
by
and
where
and
are constants, we mean an unbounded vertical cylinder with the
-axis as its radial axis; a plane making a constant angle
with the
-plane; and an unbounded horizontal plane parallel to the
-plane, respectively. This means that the circular cylinder
in rectangular coordinates can be represented simply as
in cylindrical coordinates. (Refer to Cylindrical and Spherical Coordinates for more review.)
Triple integrals can often be more readily evaluated by using cylindrical coordinates instead of rectangular coordinates. Some common equations of surfaces in rectangular coordinates along with corresponding equations in cylindrical coordinates are listed in [link]. These equations will become handy as we proceed with solving problems using triple integrals.
| Circular cylinder | Circular cone | Sphere | Paraboloid | |
|---|---|---|---|---|
| Rectangular | ||||
| Cylindrical |
As before, we start with the simplest bounded region
in
to describe in cylindrical coordinates, in the form of a cylindrical box,
([link]). Suppose we divide each interval into
subdivisions such that
and
Then we can state the following definition for a triple integral in cylindrical coordinates.
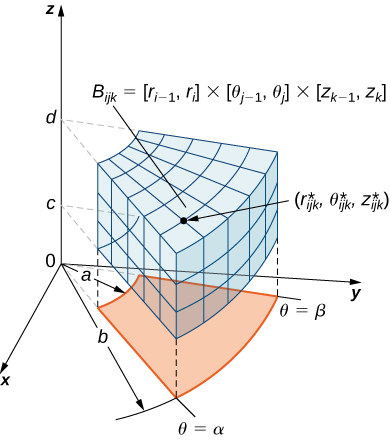
Consider the cylindrical box (expressed in cylindrical coordinates)
If the function
is continuous on
and if
is any sample point in the cylindrical subbox
([link]), then we can define the triple integral in cylindrical coordinates as the limit of a triple Riemann sum, provided the following limit exists:
Note that if
is the function in rectangular coordinates and the box
is expressed in rectangular coordinates, then the triple integral
is equal to the triple integral
and we have
As mentioned in the preceding section, all the properties of a double integral work well in triple integrals, whether in rectangular coordinates or cylindrical coordinates. They also hold for iterated integrals. To reiterate, in cylindrical coordinates, Fubini’s theorem takes the following form:
Suppose that
is continuous on a rectangular box
which when described in cylindrical coordinates looks like
Then
and
The iterated integral may be replaced equivalently by any one of the other five iterated integrals obtained by integrating with respect to the three variables in other orders.
Cylindrical coordinate systems work well for solids that are symmetric around an axis, such as cylinders and cones. Let us look at some examples before we define the triple integral in cylindrical coordinates on general cylindrical regions.
Evaluate the triple integral
where the cylindrical box
is
As stated in Fubini’s theorem, we can write the triple integral as the iterated integral
The evaluation of the iterated integral is straightforward. Each variable in the integral is independent of the others, so we can integrate each variable separately and multiply the results together. This makes the computation much easier:
Evaluate the triple integral
Follow the same steps as in the previous example.
If the cylindrical region over which we have to integrate is a general solid, we look at the projections onto the coordinate planes. Hence the triple integral of a continuous function
over a general solid region
in
where
is the projection of
onto the
-plane, is
In particular, if
then we have
Similar formulas exist for projections onto the other coordinate planes. We can use polar coordinates in those planes if necessary.
Consider the region
inside the right circular cylinder with equation
bounded below by the
-plane and bounded above by the sphere with radius
centered at the origin ([link]). Set up a triple integral over this region with a function
in cylindrical coordinates.
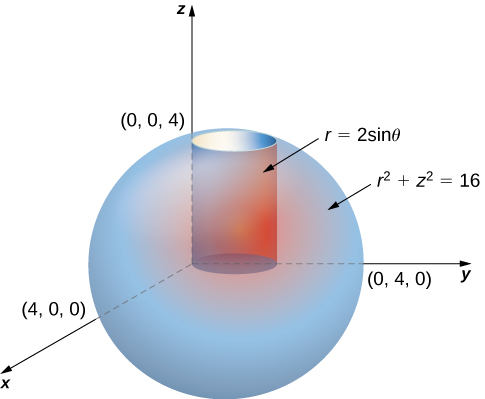
First, identify that the equation for the sphere is
We can see that the limits for
are from
to
Then the limits for
are from
to
Finally, the limits for
are from
to
Hence the region is
Therefore, the triple integral is
Consider the region
inside the right circular cylinder with equation
bounded below by the
-plane and bounded above by
Set up a triple integral with a function
in cylindrical coordinates.
Analyze the region, and draw a sketch.
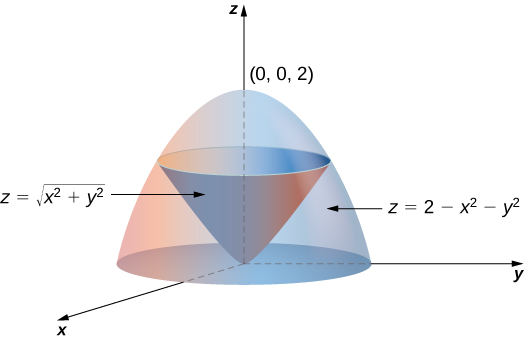
Let
be the region bounded below by the cone
and above by the paraboloid
([link]). Set up a triple integral in cylindrical coordinates to find the volume of the region, using the following orders of integration:
and
(assuming
is nonnegative), we have
Solving, we have
Since
we have
Therefore
So the intersection of these two surfaces is a circle of radius
in the plane
The cone is the lower bound for
and the paraboloid is the upper bound. The projection of the region onto the
-plane is the circle of radius
centered at the origin.
Thus, we can describe the region as
Hence the integral for the volume is
and the paraboloid as
The lower bound for
is zero, but the upper bound is sometimes the cone and the other times it is the paraboloid. The plane
divides the region into two regions. Then the region can be described as
Now the integral for the volume becomes
Redo the previous example with the order of integration
and
Note that
is independent of
and
Let E be the region bounded below by the
-plane, above by the sphere
and on the sides by the cylinder
([link]). Set up a triple integral in cylindrical coordinates to find the volume of the region using the following orders of integration, and in each case find the volume and check that the answers are the same:
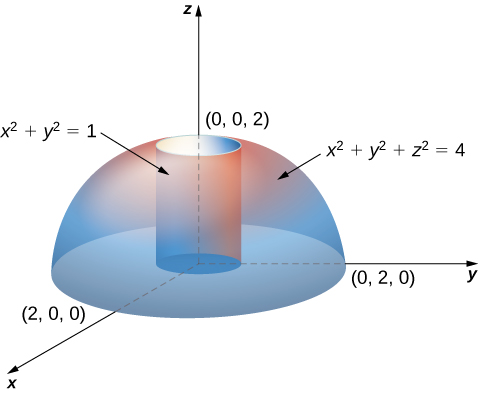
and the equation for the cylinder is
Thus, we have for the region
Hence the integral for the volume is
which is
and the cylinder is
which is
we have
that is,
Thus we have two regions, since the sphere and the cylinder intersect at
in the
-plane
and
Hence the integral for the volume is
Redo the previous example with the order of integration
and
A figure can be helpful. Note that
is independent of
and
In three-dimensional space
in the spherical coordinate system, we specify a point
by its distance
from the origin, the polar angle
from the positive
(same as in the cylindrical coordinate system), and the angle
from the positive
and the line
([link]). Note that
and
(Refer to Cylindrical and Spherical Coordinates for a review.) Spherical coordinates are useful for triple integrals over regions that are symmetric with respect to the origin.
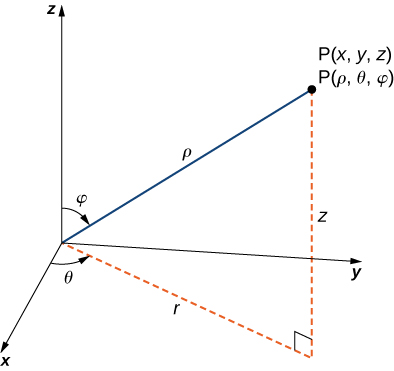
Recall the relationships that connect rectangular coordinates with spherical coordinates.
From spherical coordinates to rectangular coordinates:
From rectangular coordinates to spherical coordinates:
Other relationships that are important to know for conversions are
and
The following figure shows a few solid regions that are convenient to express in spherical coordinates.
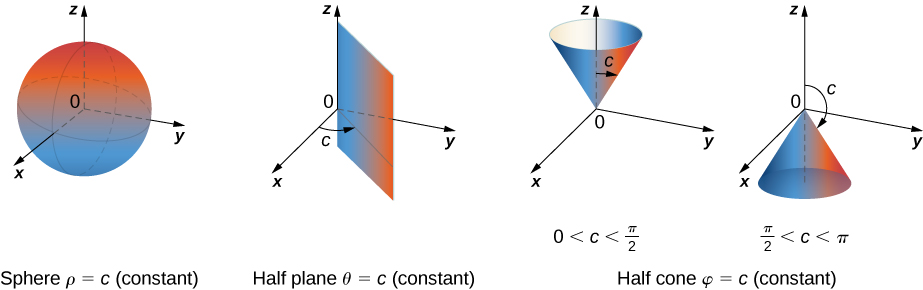
We now establish a triple integral in the spherical coordinate system, as we did before in the cylindrical coordinate system. Let the function
be continuous in a bounded spherical box,
We then divide each interval into
subdivisions such that
Now we can illustrate the following theorem for triple integrals in spherical coordinates with
being any sample point in the spherical subbox
For the volume element of the subbox
in spherical coordinates, we have
as shown in the following figure.
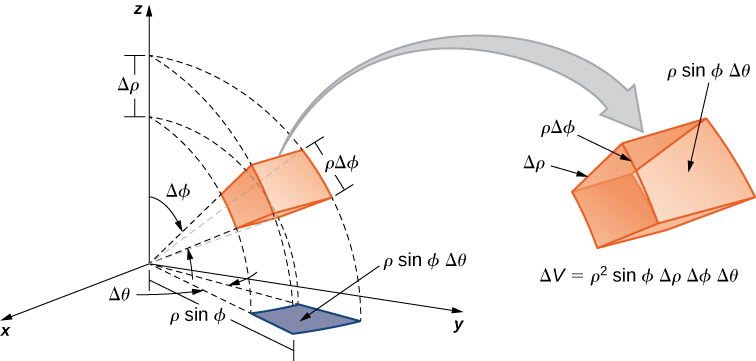
The triple integral in spherical coordinates is the limit of a triple Riemann sum,
provided the limit exists.
As with the other multiple integrals we have examined, all the properties work similarly for a triple integral in the spherical coordinate system, and so do the iterated integrals. Fubini’s theorem takes the following form.
If
is continuous on a spherical solid box
then
This iterated integral may be replaced by other iterated integrals by integrating with respect to the three variables in other orders.
As stated before, spherical coordinate systems work well for solids that are symmetric around a point, such as spheres and cones. Let us look at some examples before we consider triple integrals in spherical coordinates on general spherical regions.
Evaluate the iterated triple integral
As before, in this case the variables in the iterated integral are actually independent of each other and hence we can integrate each piece and multiply:
The concept of triple integration in spherical coordinates can be extended to integration over a general solid, using the projections onto the coordinate planes. Note that
and
mean the increments in volume and area, respectively. The variables
and
are used as the variables for integration to express the integrals.
The triple integral of a continuous function
over a general solid region
in
where
is the projection of
onto the
-plane, is
In particular, if
then we have
Similar formulas occur for projections onto the other coordinate planes.
Set up an integral for the volume of the region bounded by the cone
and the hemisphere
(see the figure below).
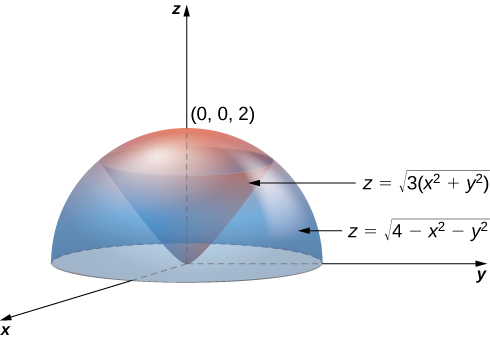
Using the conversion formulas from rectangular coordinates to spherical coordinates, we have:
For the cone:
or
or
or
For the sphere:
or
or
or
Thus, the triple integral for the volume is
Set up a triple integral for the volume of the solid region bounded above by the sphere
and bounded below by the cone
Follow the steps of the previous example.
Let
be the region bounded below by the cone
and above by the sphere
([link]). Set up a triple integral in spherical coordinates and find the volume of the region using the following orders of integration:
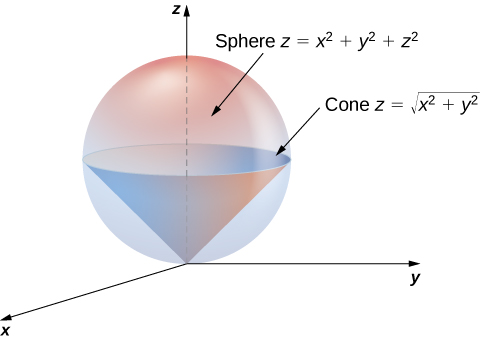
For the sphere:
For the cone:
Hence the integral for the volume of the solid region
becomes
-plane. Note that the ranges for
and
(from part a.) are
The curve
meets the line
at the point
Thus, to change the order of integration, we need to use two pieces:
Hence the integral for the volume of the solid region
becomes
In each case, the integration results in
Before we end this section, we present a couple of examples that can illustrate the conversion from rectangular coordinates to cylindrical coordinates and from rectangular coordinates to spherical coordinates.
Convert the following integral into cylindrical coordinates:
The ranges of the variables are
The first two inequalities describe the right half of a circle of radius
Therefore, the ranges for
and
are
The limits of
are
hence
Convert the following integral into spherical coordinates:
The ranges of the variables are
The first two ranges of variables describe a quarter disk in the first quadrant of the
-plane. Hence the range for
is
The lower bound
is the upper half of a cone and the upper bound
is the upper half of a sphere. Therefore, we have
which is
For the ranges of
we need to find where the cone and the sphere intersect, so solve the equation
This gives
Putting this together, we obtain
Use rectangular, cylindrical, and spherical coordinates to set up triple integrals for finding the volume of the region inside the sphere
but outside the cylinder
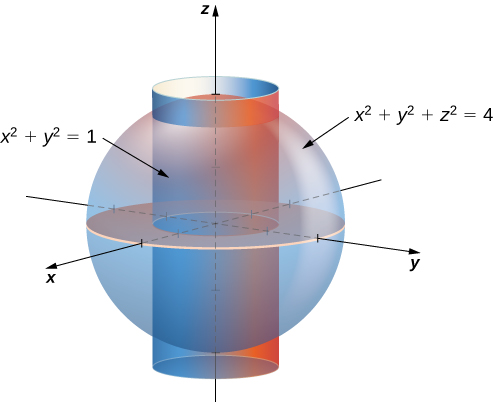
Rectangular:
Cylindrical:
Spherical:
Now that we are familiar with the spherical coordinate system, let’s find the volume of some known geometric figures, such as spheres and ellipsoids.
Find the volume of the spherical planetarium in l’Hemisphèric in Valencia, Spain, which is five stories tall and has a radius of approximately
ft, using the equation

We calculate the volume of the ball in the first octant, where
and
using spherical coordinates, and then multiply the result by
for symmetry. Since we consider the region
as the first octant in the integral, the ranges of the variables are
Therefore,
This exactly matches with what we knew. So for a sphere with a radius of approximately
ft, the volume is
For the next example we find the volume of an ellipsoid.
Find the volume of the ellipsoid
We again use symmetry and evaluate the volume of the ellipsoid using spherical coordinates. As before, we use the first octant
and
and then multiply the result by
In this case the ranges of the variables are
Also, we need to change the rectangular to spherical coordinates in this way:
Then the volume of the ellipsoid becomes
Find the volume of the space inside the ellipsoid
and outside the sphere
This problem is directly related to the l’Hemisphèric structure. The volume of space inside the ellipsoid and outside the sphere might be useful to find the expense of heating or cooling that space. We can use the preceding two examples for the volume of the sphere and ellipsoid and then substract.
First we find the volume of the ellipsoid using
and
in the result from [link]. Hence the volume of the ellipsoid is
From [link], the volume of the sphere is
Therefore, the volume of the space inside the ellipsoid
and outside the sphere
is approximately
Hot air ballooning is a relaxing, peaceful pastime that many people enjoy. Many balloonist gatherings take place around the world, such as the Albuquerque International Balloon Fiesta. The Albuquerque event is the largest hot air balloon festival in the world, with over
balloons participating each year.

As the name implies, hot air balloons use hot air to generate lift. (Hot air is less dense than cooler air, so the balloon floats as long as the hot air stays hot.) The heat is generated by a propane burner suspended below the opening of the basket. Once the balloon takes off, the pilot controls the altitude of the balloon, either by using the burner to heat the air and ascend or by using a vent near the top of the balloon to release heated air and descend. The pilot has very little control over where the balloon goes, however—balloons are at the mercy of the winds. The uncertainty over where we will end up is one of the reasons balloonists are attracted to the sport.
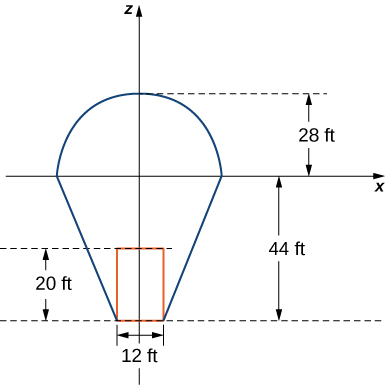
In this project we use triple integrals to learn more about hot air balloons. We model the balloon in two pieces. The top of the balloon is modeled by a half sphere of radius
feet. The bottom of the balloon is modeled by a frustum of a cone (think of an ice cream cone with the pointy end cut off). The radius of the large end of the frustum is
feet and the radius of the small end of the frustum is
feet. A graph of our balloon model and a cross-sectional diagram showing the dimensions are shown in the following figure.
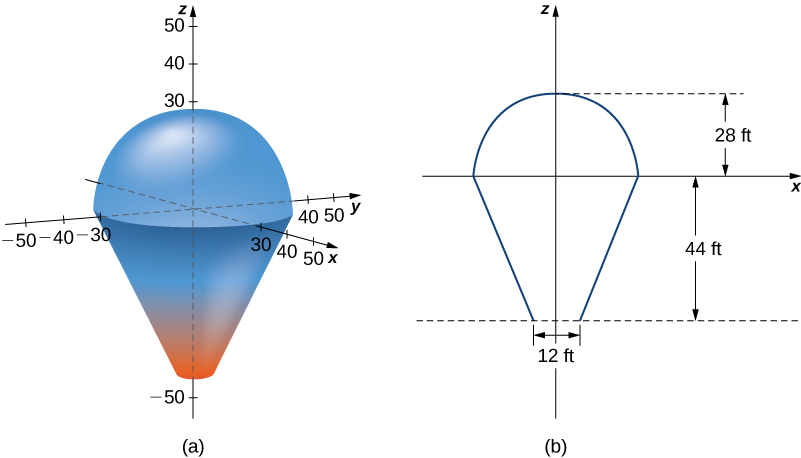
We first want to find the volume of the balloon. If we look at the top part and the bottom part of the balloon separately, we see that they are geometric solids with known volume formulas. However, it is still worthwhile to set up and evaluate the integrals we would need to find the volume. If we calculate the volume using integration, we can use the known volume formulas to check our answers. This will help ensure that we have the integrals set up correctly for the later, more complicated stages of the project.
and for the volume of a cone,
In reality, calculating the temperature at a point inside the balloon is a tremendously complicated endeavor. In fact, an entire branch of physics (thermodynamics) is devoted to studying heat and temperature. For the purposes of this project, however, we are going to make some simplifying assumptions about how temperature varies from point to point within the balloon. Assume that just prior to liftoff, the temperature (in degrees Fahrenheit) of the air inside the balloon varies according to the function
Now the pilot activates the burner for
seconds. This action affects the temperature in a
-foot-wide column
feet high, directly above the burner. A cross section of the balloon depicting this column in shown in the following figure.
Assume that after the pilot activates the burner for
seconds, the temperature of the air in the column described above increases according to the formula
Then the temperature of the air in the column is given by
while the temperature in the remainder of the balloon is still given by
seconds.
In the following exercises, evaluate the triple integrals
over the solid
be a cylindrical shell with inner radius
outer radius
and height
where
and
Assume that a function
defined on
can be expressed in cylindrical coordinates as
where
and
are differentiable functions. If
and
where
and
are antiderivatives of
and
respectively, show that
where
is a cylindrical shell with inner radius
outer radius
and height
be a cylindrical shell with inner radius
outer radius
and height
where
and
Assume that a function
defined on
can be expressed in cylindrical coordinates as
where
are differentiable functions. If
where
is an antiderivative of
show that
where
and
are antiderivatives of
and
respectively.
where
is a cylindrical shell with inner radius
outer radius
and height
In the following exercises, the boundaries of the solid
are given in cylindrical coordinates.
in cylindrical coordinates.
to cylindrical coordinates.
E is bounded by the right circular cylinder
the
-plane, and the sphere
a.
b.
is bounded by the right circular cylinder
the
-plane, and the sphere
is located in the first octant and is bounded by the circular paraboloid
the cylinder
and the plane
a.
b.
is located in the first octant outside the circular paraboloid
and inside the cylinder
and is bounded also by the planes
and
In the following exercises, the function
and region
are given.
and the function
in cylindrical coordinates.
into cylindrical coordinates and evaluate it.
a.
b.
a.
b.
In the following exercises, find the volume of the solid
whose boundaries are given in rectangular coordinates.
is above the
-plane, inside the cylinder
and below the plane
is below the plane
and inside the paraboloid
is bounded by the circular cone
and
is located above the
-plane, below
outside the one-sheeted hyperboloid
and inside the cylinder
is located inside the cylinder
and between the circular paraboloids
and
is located inside the sphere
above the
-plane, and inside the circular cone
is located outside the circular cone
and between the planes
and
is located outside the circular cone
above the
-plane, below the circular paraboloid, and between the planes
[T] Use a computer algebra system (CAS) to graph the solid whose volume is given by the iterated integral in cylindrical coordinates
Find the volume
of the solid. Round your answer to four decimal places.
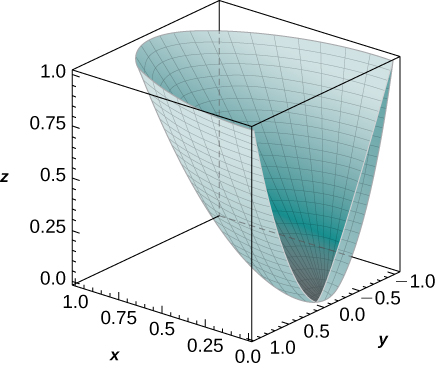
[T] Use a CAS to graph the solid whose volume is given by the iterated integral in cylindrical coordinates
Find the volume
of the solid Round your answer to four decimal places.
Convert the integral
into an integral in cylindrical coordinates.
Convert the integral
into an integral in cylindrical coordinates.
In the following exercises, evaluate the triple integral
over the solid
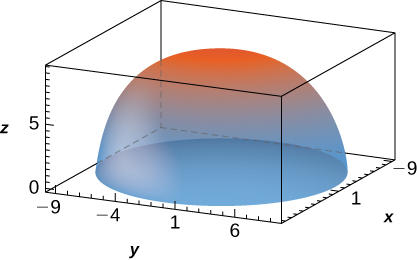
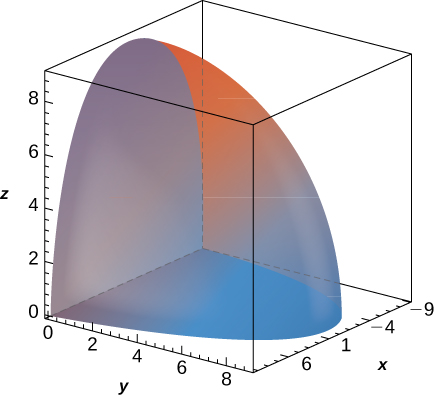
is bounded above by the half-sphere
with
and below by the cone
is bounded above by the half-sphere
with
and below by the cone
Show that if
is a continuous function on the spherical box
then
is said to have spherical symmetry if it depends on the distance to the origin only, that is, it can be expressed in spherical coordinates as
where
Show that
where
is the region between the upper concentric hemispheres of radii
and
centered at the origin, with
and
a spherical function defined on
where
be the region between the upper concentric hemispheres of radii a and b centered at the origin and situated in the first octant, where
Consider F a function defined on B whose form in spherical coordinates
is
Show that if
and
then
where
is an antiderivative of
and
is an antiderivative of
where
is the region between the upper concentric hemispheres of radii
and
centered at the origin and situated in the first octant.
In the following exercises, the function
and region
are given.
and function
in cylindrical coordinates.
into cylindrical coordinates and evaluate it.
a.
b.
a.
b.
In the following exercises, find the volume of the solid
whose boundaries are given in rectangular coordinates.
Use spherical coordinates to find the volume of the solid situated outside the sphere
and inside the sphere
with
Use spherical coordinates to find the volume of the ball
that is situated between the cones
Convert the integral
into an integral in spherical coordinates.
Convert the integral
into an integral in spherical coordinates.
Convert the integral
into an integral in spherical coordinates and evaluate it.
[T] Use a CAS to graph the solid whose volume is given by the iterated integral in spherical coordinates
Find the volume
of the solid. Round your answer to three decimal places.
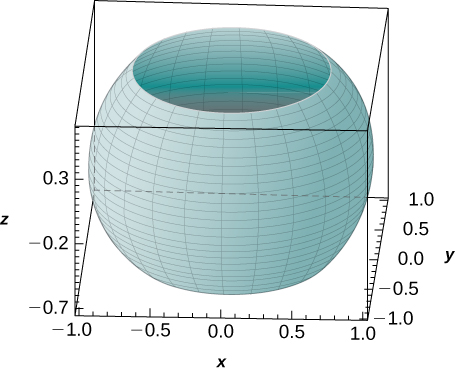
[T] Use a CAS to graph the solid whose volume is given by the iterated integral in spherical coordinates as
Find the volume
of the solid. Round your answer to three decimal places.
[T] Use a CAS to evaluate the integral
where
lies above the paraboloid
and below the plane
[T]
where
is bounded by the spheres
and
Express the volume of the solid inside the sphere
and outside the cylinder
as triple integrals in cylindrical coordinates and spherical coordinates, respectively.
Express the volume of the solid inside the sphere
and outside the cylinder
that is located in the first octant as triple integrals in cylindrical coordinates and spherical coordinates, respectively.
The power emitted by an antenna has a power density per unit volume given in spherical coordinates by
where
is a constant with units in watts. The total power within a sphere
of radius
meters is defined as
Find the total power
watts
Use the preceding exercise to find the total power within a sphere
of radius 5 meters when the power density per unit volume is given by
A charge cloud contained in a sphere
of radius r centimeters centered at the origin has its charge density given by
where
The total charge contained in
is given by
Find the total charge
Use the preceding exercise to find the total charge cloud contained in the unit sphere if the charge density is

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: