Double integrals are sometimes much easier to evaluate if we change rectangular coordinates to polar coordinates. However, before we describe how to make this change, we need to establish the concept of a double integral in a polar rectangular region.
When we defined the double integral for a continuous function in rectangular coordinates—say,
over a region
in the
-plane—we divided
into subrectangles with sides parallel to the coordinate axes. These sides have either constant
-values and/or constant
-values. In polar coordinates, the shape we work with is a polar rectangle, whose sides have constant
-values and/or constant
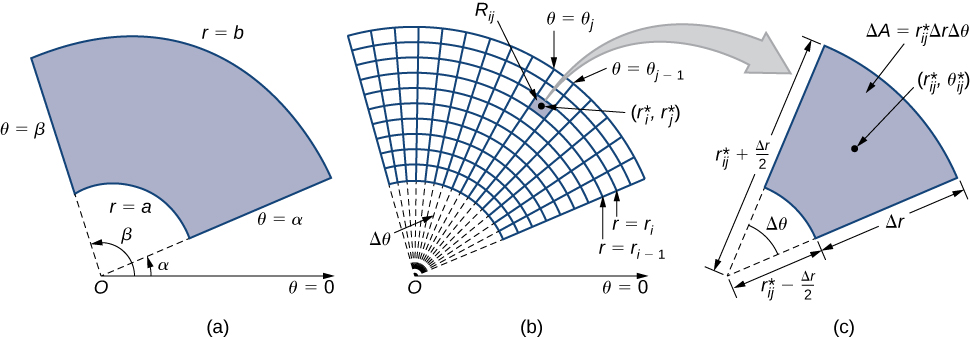
-values. This means we can describe a polar rectangle as in [link](a), with
In this section, we are looking to integrate over polar rectangles. Consider a function
over a polar rectangle
We divide the interval
into
subintervals
of length
and divide the interval
into
subintervals
of width
This means that the circles
and rays
for
and
divide the polar rectangle
into smaller polar subrectangles
([link](b)).

As before, we need to find the area
of the polar subrectangle
and the “polar” volume of the thin box above
Recall that, in a circle of radius
the length
of an arc subtended by a central angle of
radians is
Notice that the polar rectangle
looks a lot like a trapezoid with parallel sides
and
and with a width
Hence the area of the polar subrectangle
is
Simplifying and letting
we have
Therefore, the polar volume of the thin box above
([link]) is
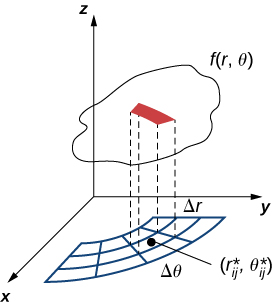
Using the same idea for all the subrectangles and summing the volumes of the rectangular boxes, we obtain a double Riemann sum as
As we have seen before, we obtain a better approximation to the polar volume of the solid above the region
when we let
and
become larger. Hence, we define the polar volume as the limit of the double Riemann sum,
This becomes the expression for the double integral.
The double integral of the function
over the polar rectangular region
in the
-plane is defined as
Again, just as in Double Integrals over Rectangular Regions, the double integral over a polar rectangular region can be expressed as an iterated integral in polar coordinates. Hence,
Notice that the expression for
is replaced by
when working in polar coordinates. Another way to look at the polar double integral is to change the double integral in rectangular coordinates by substitution. When the function
is given in terms of
and
using
changes it to
Note that all the properties listed in Double Integrals over Rectangular Regions for the double integral in rectangular coordinates hold true for the double integral in polar coordinates as well, so we can use them without hesitation.
Sketch the polar rectangular region
As we can see from [link],
and
are circles of radius
and
covers the entire top half of the plane. Hence the region
looks like a semicircular band.
Now that we have sketched a polar rectangular region, let us demonstrate how to evaluate a double integral over this region by using polar coordinates.
Evaluate the integral
over the region
First we sketch a figure similar to [link] but with outer radius
From the figure we can see that we have
Evaluate the integral
where
is the unit circle on the
-plane.
The region
is a unit circle, so we can describe it as
Using the conversion
and
we have
Evaluate the integral
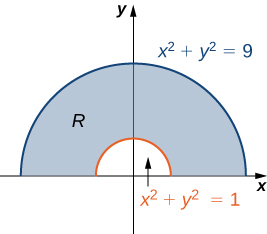
where
We can see that
is an annular region that can be converted to polar coordinates and described as
(see the following graph).
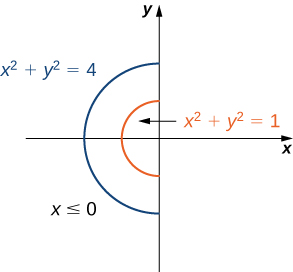
Hence, using the conversion
and
we have
Evaluate the integral
where
is the circle of radius
on the
-plane.
Follow the steps in the previous example.
To evaluate the double integral of a continuous function by iterated integrals over general polar regions, we consider two types of regions, analogous to Type I and Type II as discussed for rectangular coordinates in Double Integrals over General Regions. It is more common to write polar equations as
than
so we describe a general polar region as
(see the following figure).
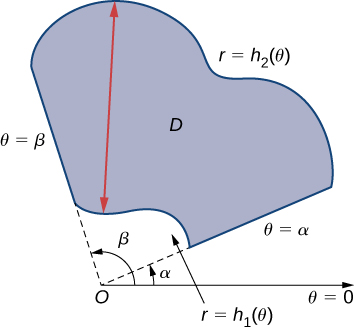
If
is continuous on a general polar region
as described above, then
Evaluate the integral
where
is the region bounded by the polar axis and the upper half of the cardioid
We can describe the region
as
as shown in the following figure.
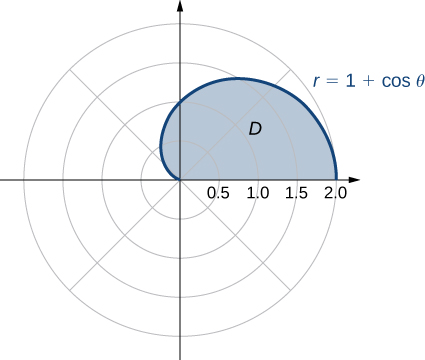
Hence, we have
Evaluate the integral
Graph the region and follow the steps in the previous example.
As in rectangular coordinates, if a solid
is bounded by the surface
as well as by the surfaces
and
we can find the volume
of
by double integration, as
If the base of the solid can be described as
then the double integral for the volume becomes
We illustrate this idea with some examples.
Find the volume of the solid that lies under the paraboloid
and above the unit circle on the
-plane (see the following figure).
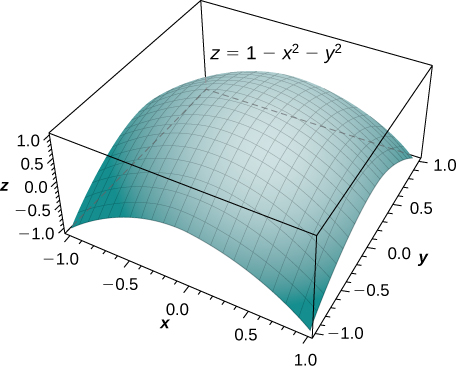
By the method of double integration, we can see that the volume is the iterated integral of the form
where
This integration was shown before in [link], so the volume is
cubic units.
Find the volume of the solid that lies under the paraboloid
and above the disk
on the
-plane. See the paraboloid in [link] intersecting the cylinder
above the
-plane.
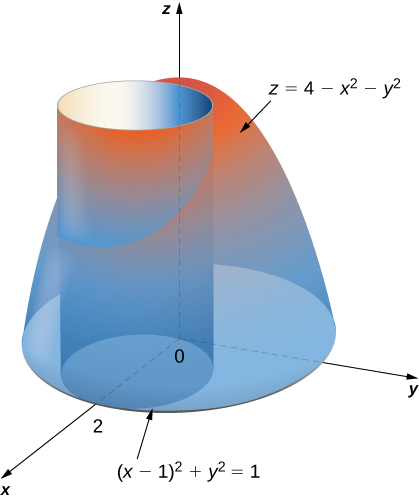
First change the disk
to polar coordinates. Expanding the square term, we have
Then simplify to get
which in polar coordinates becomes
and then either
or
Similarly, the equation of the paraboloid changes to
Therefore we can describe the disk
on the
-plane as the region
Hence the volume of the solid bounded above by the paraboloid
and below by
is
Notice in the next example that integration is not always easy with polar coordinates. Complexity of integration depends on the function and also on the region over which we need to perform the integration. If the region has a more natural expression in polar coordinates or if
has a simpler antiderivative in polar coordinates, then the change in polar coordinates is appropriate; otherwise, use rectangular coordinates.
Find the volume of the region that lies under the paraboloid
and above the triangle enclosed by the lines
and
in the
-plane ([link]).
First examine the region over which we need to set up the double integral and the accompanying paraboloid.
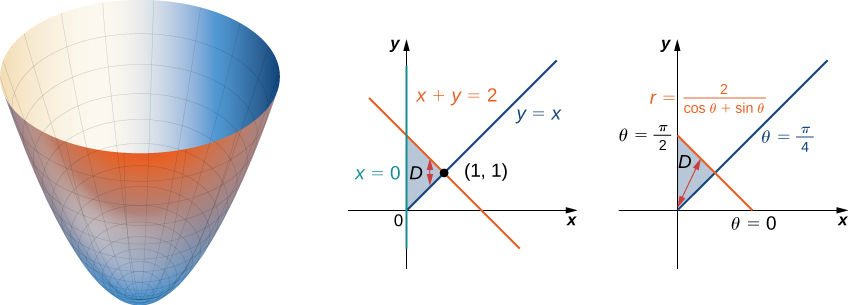
The region
is
Converting the lines
and
in the
-plane to functions of
and
we have
and
respectively. Graphing the region on the
-plane, we see that it looks like
Now converting the equation of the surface gives
Therefore, the volume of the solid is given by the double integral
As you can see, this integral is very complicated. So, we can instead evaluate this double integral in rectangular coordinates as
Evaluating gives
To answer the question of how the formulas for the volumes of different standard solids such as a sphere, a cone, or a cylinder are found, we want to demonstrate an example and find the volume of an arbitrary cone.
Use polar coordinates to find the volume inside the cone
and above the
The region
for the integration is the base of the cone, which appears to be a circle on the
(see the following figure).
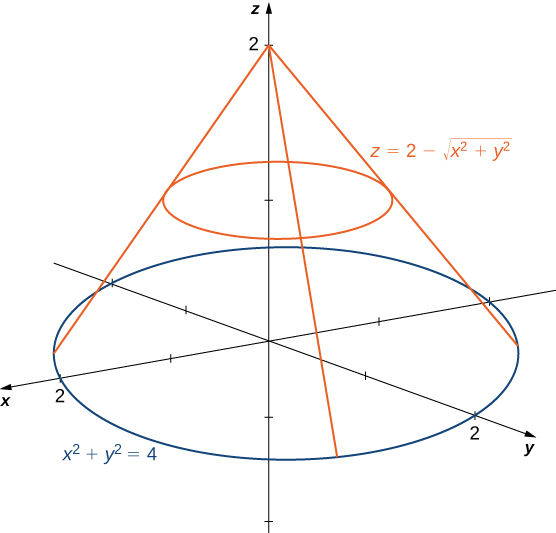
We find the equation of the circle by setting
This means the radius of the circle is
so for the integration we have
and
Substituting
and
in the equation
we have
Therefore, the volume of the cone is
cubic units.
Note that if we were to find the volume of an arbitrary cone with radius
units and height
units, then the equation of the cone would be
We can still use [link] and set up the integral as
Evaluating the integral, we get
Use polar coordinates to find an iterated integral for finding the volume of the solid enclosed by the paraboloids
and
cubic units
Sketching the graphs can help.
As with rectangular coordinates, we can also use polar coordinates to find areas of certain regions using a double integral. As before, we need to understand the region whose area we want to compute. Sketching a graph and identifying the region can be helpful to realize the limits of integration. Generally, the area formula in double integration will look like
Evaluate the area bounded by the curve
Sketching the graph of the function
reveals that it is a polar rose with eight petals (see the following figure).
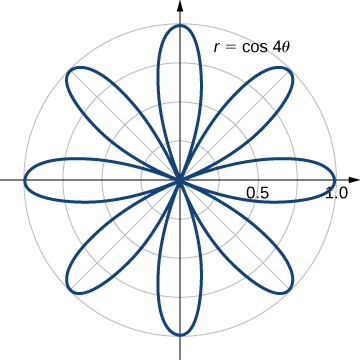
Using symmetry, we can see that we need to find the area of one petal and then multiply it by
Notice that the values of
for which the graph passes through the origin are the zeros of the function
and these are odd multiples of
Thus, one of the petals corresponds to the values of
in the interval
Therefore, the area bounded by the curve
is
Find the area enclosed by the circle
and the cardioid
First and foremost, sketch the graphs of the region ([link]).
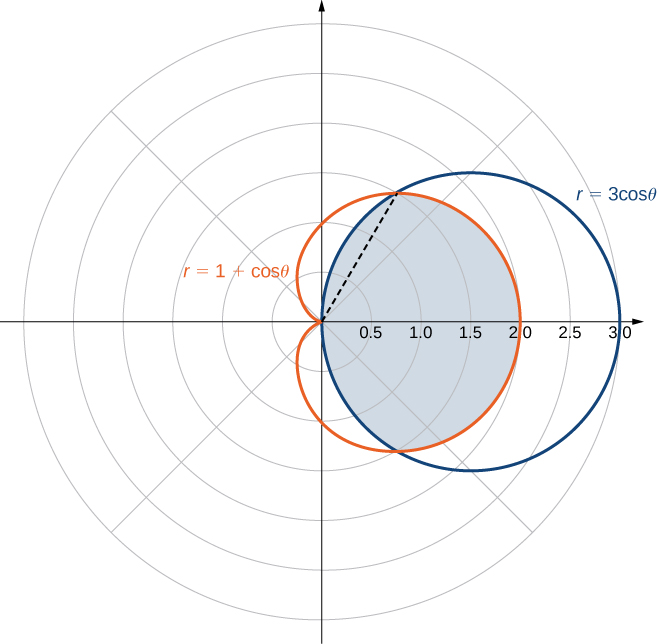
We can from see the symmetry of the graph that we need to find the points of intersection. Setting the two equations equal to each other gives
One of the points of intersection is
The area above the polar axis consists of two parts, with one part defined by the cardioid from
to
and the other part defined by the circle from
to
By symmetry, the total area is twice the area above the polar axis. Thus, we have
Evaluating each piece separately, we find that the area is
Find the area enclosed inside the cardioid
and outside the cardioid
Sketch the graph, and solve for the points of intersection.
Evaluate the integral
This is an improper integral because we are integrating over an unbounded region
In polar coordinates, the entire plane
can be seen as
Using the changes of variables from rectangular coordinates to polar coordinates, we have
Evaluate the integral
Convert to the polar coordinate system.
in polar coordinates becomes
and
to convert an integral in rectangular coordinates to an integral in polar coordinates.
and
to convert an integral in polar coordinates to an integral in rectangular coordinates, if needed.
over a region on the
-plane, use a double integral in polar coordinates.
**Double integral over a polar rectangular region
**
Double integral over a general polar region
In the following exercises, express the region
in polar coordinates.
is the region of the disk of radius
centered at the origin that lies in the first quadrant.
is the region between the circles of radius
and radius
centered at the origin that lies in the second quadrant.
is the region bounded by the
-axis and
is the region bounded by the
-axis and
In the following exercises, the graph of the polar rectangular region
is given. Express
in polar coordinates.
In the following graph, the region
is situated below
and is bounded by
and
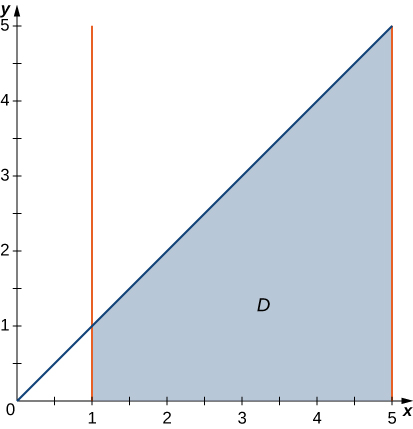
In the following graph, the region
is bounded by
and
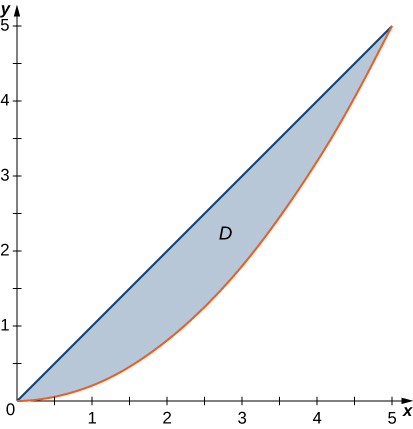
In the following exercises, evaluate the double integral
over the polar rectangular region
where
where
where
where
In the following exercises, the integrals have been converted to polar coordinates. Verify that the identities are true and choose the easiest way to evaluate the integrals, in rectangular or polar coordinates.
In the following exercises, convert the integrals to polar coordinates and evaluate them.
Evaluate the integral
where
is the region bounded by the polar axis and the upper half of the cardioid
Find the area of the region
bounded by the polar axis and the upper half of the cardioid
Evaluate the integral
where
is the region bounded by the part of the four-leaved rose
situated in the first quadrant (see the following figure).
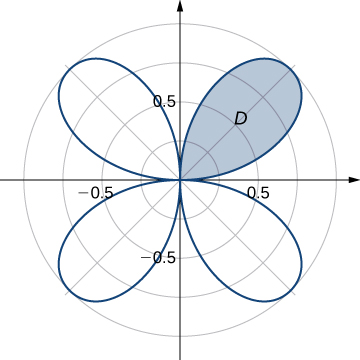
Find the total area of the region enclosed by the four-leaved rose
(see the figure in the previous exercise).
Find the area of the region
which is the region bounded by
and
Find the area of the region
which is the region inside the disk
and to the right of the line
Determine the average value of the function
over the region
bounded by the polar curve
where
(see the following graph).
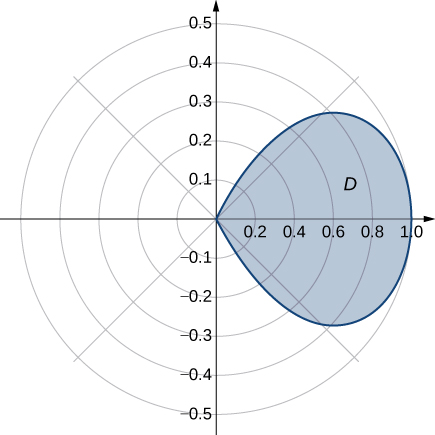
Determine the average value of the function
over the region
bounded by the polar curve
where
(see the following graph).
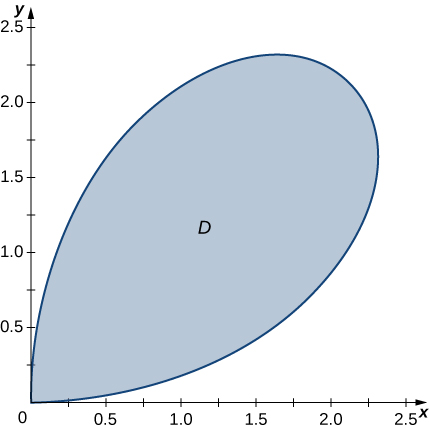
Find the volume of the solid situated in the first octant and bounded by the paraboloid
and the planes
and
Find the volume of the solid bounded by the paraboloid
and the plane
bounded by the cylinder
and the planes
and
outside the double cone
inside the cylinder
and above the plane
and below the plane
by subtracting the volumes of the solids
and
inside the unit sphere
and above the plane
inside the double cone
and above the plane
and inside the sphere
a.
b.
c.
For the following two exercises, consider a spherical ring, which is a sphere with a cylindrical hole cut so that the axis of the cylinder passes through the center of the sphere (see the following figure).

If the sphere has radius
and the cylinder has radius
find the volume of the spherical ring.
A cylindrical hole of diameter
cm is bored through a sphere of radius
cm such that the axis of the cylinder passes through the center of the sphere. Find the volume of the resulting spherical ring.
Find the volume of the solid that lies under the double cone
inside the cylinder
and above the plane
Find the volume of the solid that lies under the paraboloid
inside the cylinder
and above the plane
Find the volume of the solid that lies under the plane
and above the disk
Find the volume of the solid that lies under the plane
and above the unit disk
A radial function
is a function whose value at each point depends only on the distance between that point and the origin of the system of coordinates; that is,
where
Show that if
is a continuous radial function, then
where
and
with
and
Use the information from the preceding exercise to calculate the integral
where
is the unit disk.
Let
be a continuous radial function defined on the annular region
where
and
is a differentiable function. Show that
Apply the preceding exercise to calculate the integral
where
is the annular region between the circles of radii
and
situated in the third quadrant.
Let
be a continuous function that can be expressed in polar coordinates as a function of
only; that is,
where
with
and
Show that
where
is an antiderivative of
Apply the preceding exercise to calculate the integral
where
Let
be a continuous function that can be expressed in polar coordinates as a function of
only; that is,
where
with
and
Show that
where
and
are antiderivatives of
and
respectively.
Evaluate
where
A spherical cap is the region of a sphere that lies above or below a given plane.
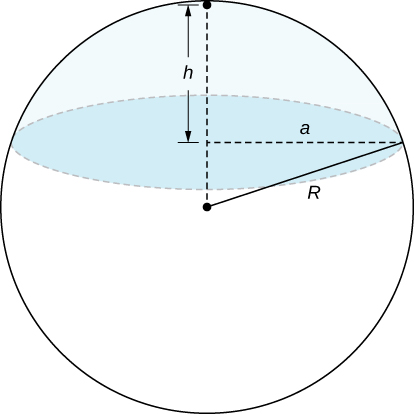
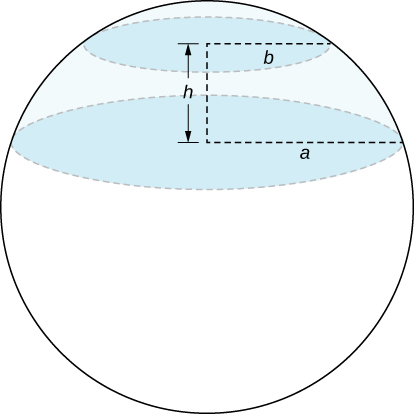
show that the volume of the spherical segment in the figure below is
In statistics, the joint density for two independent, normally distributed events with a mean
and a standard distribution
is defined by
Consider
the Cartesian coordinates of a ball in the resting position after it was released from a position on the z-axis toward the
-plane. Assume that the coordinates of the ball are independently normally distributed with a mean
and a standard deviation of
(in feet). The probability that the ball will stop no more than
feet from the origin is given by
where
is the disk of radius a centered at the origin. Show that
The double improper integral
may be defined as the limit value of the double integrals
over disks
of radii a centered at the origin, as a increases without bound; that is,
by using the relation
and
and the angles
and
it is described as

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: