In this section we investigate double integrals and show how we can use them to find the volume of a solid over a rectangular region in the
-plane. Many of the properties of double integrals are similar to those we have already discussed for single integrals.
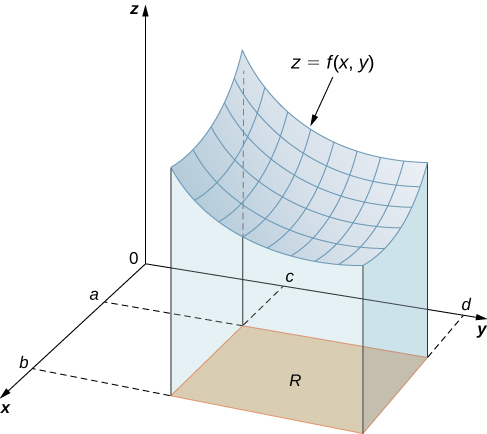
We begin by considering the space above a rectangular region R. Consider a continuous function
of two variables defined on the closed rectangle R:
Here
denotes the Cartesian product of the two closed intervals
and
It consists of rectangular pairs
such that
and
The graph of
represents a surface above the
-plane with equation
where
is the height of the surface at the point
Let
be the solid that lies above
and under the graph of
([link]). The base of the solid is the rectangle
in the
-plane. We want to find the volume
of the solid

We divide the region
into small rectangles
each with area
and with sides
and
([link]). We do this by dividing the interval
into
subintervals and dividing the interval
into
subintervals. Hence
and
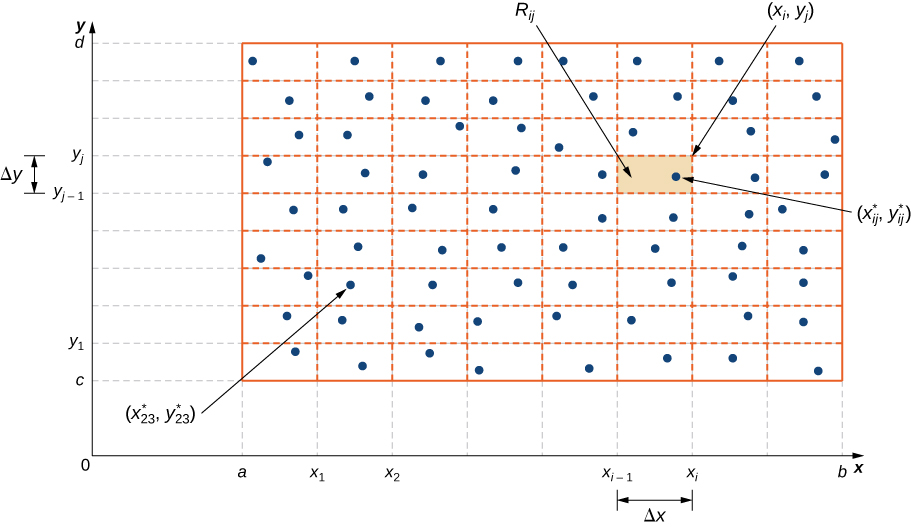
The volume of a thin rectangular box above
is
where
is an arbitrary sample point in each
as shown in the following figure.
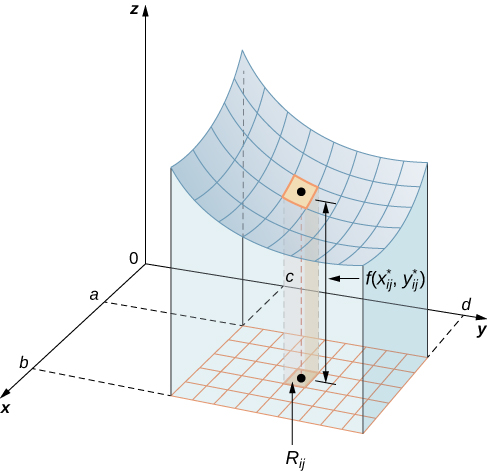
Using the same idea for all the subrectangles, we obtain an approximate volume of the solid
as
This sum is known as a double Riemann sum and can be used to approximate the value of the volume of the solid. Here the double sum means that for each subrectangle we evaluate the function at the chosen point, multiply by the area of each rectangle, and then add all the results.
As we have seen in the single-variable case, we obtain a better approximation to the actual volume if m and n become larger.
Note that the sum approaches a limit in either case and the limit is the volume of the solid with the base R. Now we are ready to define the double integral.
The double integral of the function
over the rectangular region
in the
-plane is defined as
If
then the volume V of the solid S, which lies above
in the
-plane and under the graph of f, is the double integral of the function
over the rectangle
If the function is ever negative, then the double integral can be considered a “signed” volume in a manner similar to the way we defined net signed area in The Definite Integral.
Consider the function
over the rectangular region
([link]).
and “under” the graph of
and choose the sample point as the upper right corner point of each square
and
([link]) to approximate the signed volume of the solid S that lies above
and “under” the graph of
and choose the sample point as the midpoint of each square:
to approximate the signed volume.
![The function z=f(x,y) graphed over the rectangular region R=[0,2]×[0,2]. In xyz space, there is a surface z = f(x, y) = 3x2 minus y. The corners of the surface are given as (0, 0, 0), (2, 0, 12), (0, 2, negative 2), and (2, 2, 10). The surface is parabolic along the x axis.](../resources/CNX_Calc_Figure_15_01_004.jpg)
is above the plane. To find the signed volume of S, we need to divide the region R into small rectangles
each with area
and with sides
and
and choose
as sample points in each
Hence, a double integral is set up as
we have
Also, the sample points are (1, 1), (2, 1), (1, 2), and (2, 2) as shown in the following figure.
![Subrectangles for the rectangular region R=[0,2]×[0,2]. On the xy plane, the points (1, 1), (1, 2), (2, 1), and (2, 2) are marked, and these form the upper right corners of four squares marked R11, R12, R21, and R22, respectively. Each square has area Delta A = 1.](../resources/CNX_Calc_Figure_15_01_005.jpg)
Hence,
we have
In this case the sample points are (1/2, 1/2), (3/2, 1/2), (1/2, 3/2),
and (3/2, 3/2).
Hence
Notice that the approximate answers differ due to the choices of the sample points. In either case, we are introducing some error because we are using only a few sample points. Thus, we need to investigate how we can achieve an accurate answer.
Use the same function
over the rectangular region
Divide R into the same four squares with
and choose the sample points as the upper left corner point of each square
and
([link]) to approximate the signed volume of the solid S that lies above
and “under” the graph of
Follow the steps of the previous example.
Note that we developed the concept of double integral using a rectangular region R. This concept can be extended to any general region. However, when a region is not rectangular, the subrectangles may not all fit perfectly into R, particularly if the base area is curved. We examine this situation in more detail in the next section, where we study regions that are not always rectangular and subrectangles may not fit perfectly in the region R. Also, the heights may not be exact if the surface
is curved. However, the errors on the sides and the height where the pieces may not fit perfectly within the solid S approach 0 as m and n approach infinity. Also, the double integral of the function
exists provided that the function
is not too discontinuous. If the function is bounded and continuous over R except on a finite number of smooth curves, then the double integral exists and we say that
is integrable over R.
Since
we can express
as
or
This means that, when we are using rectangular coordinates, the double integral over a region
denoted by
can be written as
or
Now let’s list some of the properties that can be helpful to compute double integrals.
The properties of double integrals are very helpful when computing them or otherwise working with them. We list here six properties of double integrals. Properties 1 and 2 are referred to as the linearity of the integral, property 3 is the additivity of the integral, property 4 is the monotonicity of the integral, and property 5 is used to find the bounds of the integral. Property 6 is used if
is a product of two functions
and
Assume that the functions
and
are integrable over the rectangular region R; S and T are subregions of R; and assume that m and M are real numbers.
is integrable and
is integrable and
and
except an overlap on the boundaries, then
for
in
then
then
can be factored as a product of a function
of
only and a function
of
only, then over the region
the double integral can be written as
These properties are used in the evaluation of double integrals, as we will see later. We will become skilled in using these properties once we become familiar with the computational tools of double integrals. So let’s get to that now.
So far, we have seen how to set up a double integral and how to obtain an approximate value for it. We can also imagine that evaluating double integrals by using the definition can be a very lengthy process if we choose larger values for
and
Therefore, we need a practical and convenient technique for computing double integrals. In other words, we need to learn how to compute double integrals without employing the definition that uses limits and double sums.
The basic idea is that the evaluation becomes easier if we can break a double integral into single integrals by integrating first with respect to one variable and then with respect to the other. The key tool we need is called an iterated integral.
Assume
and
are real numbers. We define an iterated integral for a function
over the rectangular region
as
The notation
means that we integrate
with respect to y while holding x constant. Similarly, the notation
means that we integrate
with respect to x while holding y constant. The fact that double integrals can be split into iterated integrals is expressed in Fubini’s theorem. Think of this theorem as an essential tool for evaluating double integrals.
Suppose that
is a function of two variables that is continuous over a rectangular region
Then we see from [link] that the double integral of
over the region equals an iterated integral,
More generally, Fubini’s theorem is true if
is bounded on
and
is discontinuous only on a finite number of continuous curves. In other words,
has to be integrable over
Use Fubini’s theorem to compute the double integral
where
and
Fubini’s theorem offers an easier way to evaluate the double integral by the use of an iterated integral. Note how the boundary values of the region R become the upper and lower limits of integration.
The double integration in this example is simple enough to use Fubini’s theorem directly, allowing us to convert a double integral into an iterated integral. Consequently, we are now ready to convert all double integrals to iterated integrals and demonstrate how the properties listed earlier can help us evaluate double integrals when the function
is more complex. Note that the order of integration can be changed (see [link]).
Evaluate the double integral
where
This function has two pieces: one piece is
and the other is
Also, the second piece has a constant
Notice how we use properties i and ii to help evaluate the double integral.
Over the region
we have
Find a lower and an upper bound for the integral
For a lower bound, integrate the constant function 2 over the region
For an upper bound, integrate the constant function 13 over the region
Hence, we obtain
Evaluate the integral
over the region
This is a great example for property vi because the function
is clearly the product of two single-variable functions
and
Thus we can split the integral into two parts and then integrate each one as a single-variable integration problem.
where
a. 26 b. Answers may vary.
Use properties i. and ii. and evaluate the iterated integral, and then use property v.
As we mentioned before, when we are using rectangular coordinates, the double integral over a region
denoted by
can be written as
or
The next example shows that the results are the same regardless of which order of integration we choose.
Let’s return to the function
from [link], this time over the rectangular region
Use Fubini’s theorem to evaluate
in two different ways:
[link] shows how the calculation works in two different ways.
With either order of integration, the double integral gives us an answer of 15. We might wish to interpret this answer as a volume in cubic units of the solid
below the function
over the region
However, remember that the interpretation of a double integral as a (non-signed) volume works only when the integrand
is a nonnegative function over the base region
Evaluate
Use Fubini’s theorem.
In the next example we see that it can actually be beneficial to switch the order of integration to make the computation easier. We will come back to this idea several times in this chapter.
Consider the double integral
over the region
([link]).
![The function z=f(x,y)=xsin(xy) over the rectangular region R=[0,π]×[1,2]. The function z = f(x, y) = x sin(xy) is shown, which starts with z = 0 along the x axis. Then, the function increases roughly as a normal sin function would, but then skews a bit and decreases as x increases after pi/2.](../resources/CNX_Calc_Figure_15_01_007.jpg)
in the following two ways: first by integrating with respect to
and then with respect to
second by integrating with respect to
and then with respect to
we see that we can use the substitution
which gives
Hence the inner integral is simply
and we can change the limits to be functions of x,
However, integrating with respect to
first and then integrating with respect to
requires integration by parts for the inner integral, with
and
Then
and
so
Since the evaluation is getting complicated, we will only do the computation that is easier to do, which is clearly the first method.
Evaluate the integral
where
Integrate with respect to
first.
Double integrals are very useful for finding the area of a region bounded by curves of functions. We describe this situation in more detail in the next section. However, if the region is a rectangular shape, we can find its area by integrating the constant function
over the region
The area of the region
is given by
This definition makes sense because using
and evaluating the integral make it a product of length and width. Let’s check this formula with an example and see how this works.
Find the area of the region
by using a double integral, that is, by integrating 1 over the region
The region is rectangular with length 3 and width 2, so we know that the area is 6. We get the same answer when we use a double integral:
We have already seen how double integrals can be used to find the volume of a solid bounded above by a function
over a region
provided
for all
in
Here is another example to illustrate this concept.
Find the volume
of the solid
that is bounded by the elliptic paraboloid
the planes
and
and the three coordinate planes.
First notice the graph of the surface
in [link](a) and above the square region
However, we need the volume of the solid bounded by the elliptic paraboloid
the planes
and
and the three coordinate planes.
![(a) The surface z=27−2x2−y2 above the square region R1=[−3,3]×[−3,3]. (b) The solid S lies under the surface z=27−2x2−y2 above the square region R2=[0,3]×[0,3]. This figure consists of two figures marked a and b. In figure a, in xyz space, the surface z = 20 minus 2x2 minus y2 is shown for x and y from negative 3 to positive 3. The shape looks like a sheet that has been pinned at the corners and forced up gently in the middle. In figure b, in xyz space, the surface z = 20 minus 2x2 minus y2 is shown for x and y from 0 to positive 3. The surface is the upper corner of the figure from part a, and below the surface is marked the solid S.](../resources/CNX_Calc_Figure_15_01_008.jpg)
Now let’s look at the graph of the surface in [link](b). We determine the volume V by evaluating the double integral over
Find the volume of the solid bounded above by the graph of
and below by the
-plane on the rectangular region
Graph the function, set up the integral, and use an iterated integral.
Recall that we defined the average value of a function of one variable on an interval
as
Similarly, we can define the average value of a function of two variables over a region R. The main difference is that we divide by an area instead of the width of an interval.
The average value of a function of two variables over a region
is
In the next example we find the average value of a function over a rectangular region. This is a good example of obtaining useful information for an integration by making individual measurements over a grid, instead of trying to find an algebraic expression for a function.
The weather map in [link] shows an unusually moist storm system associated with the remnants of Hurricane Karl, which dumped 4–8 inches (100–200 mm) of rain in some parts of the Midwest on September 22–23, 2010. The area of rainfall measured 300 miles east to west and 250 miles north to south. Estimate the average rainfall over the entire area in those two days.
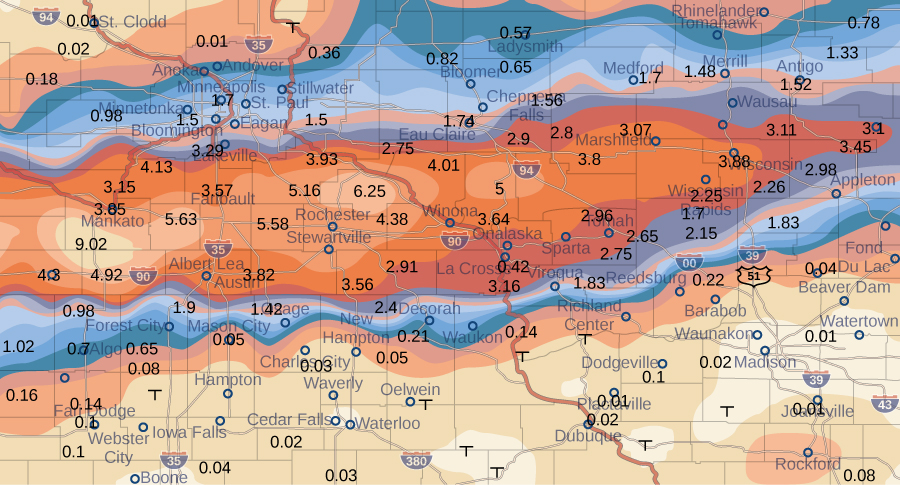
Place the origin at the southwest corner of the map so that all the values can be considered as being in the first quadrant and hence all are positive. Now divide the entire map into six rectangles
as shown in [link]. Assume
denotes the storm rainfall in inches at a point approximately
miles to the east of the origin and y miles to the north of the origin. Let
represent the entire area of
square miles. Then the area of each subrectangle is
Assume
are approximately the midpoints of each subrectangle
Note the color-coded region at each of these points, and estimate the rainfall. The rainfall at each of these points can be estimated as:
At
the rainfall is 0.08.
At
the rainfall is 0.08.
At
the rainfall is 0.01.
At
the rainfall is 1.70.
At
the rainfall is 1.74.
At
the rainfall is 3.00.
According to our definition, the average storm rainfall in the entire area during those two days was
During September 22–23, 2010 this area had an average storm rainfall of approximately 1.10 inches.
A contour map is shown for a function
on the rectangle
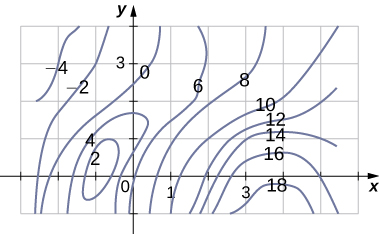
and
to estimate the value of
Answers to both parts a. and b. may vary.
Divide the region into six rectangles, and use the contour lines to estimate the values for
or
In the following exercises, use the midpoint rule with
and
to estimate the volume of the solid bounded by the surface
the vertical planes
and
and the horizontal plane
27.
In the following exercises, estimate the volume of the solid under the surface
and above the rectangular region R by using a Riemann sum with
and the sample points to be the lower left corners of the subrectangles of the partition.
0.
Use the midpoint rule with
to estimate
where the values of the function f on
are given in the following table.
| y | |||||
| x | 9 | 9.5 | 10 | 10.5 | 11 |
| 8 | 9.8 | 5 | 6.7 | 5 | 5.6 |
| 8.5 | 9.4 | 4.5 | 8 | 5.4 | 3.4 |
| 9 | 8.7 | 4.6 | 6 | 5.5 | 3.4 |
| 9.5 | 6.7 | 6 | 4.5 | 5.4 | 6.7 |
| 10 | 6.8 | 6.4 | 5.5 | 5.7 | 6.8 |
21.3.
The values of the function f on the rectangle
are given in the following table. Estimate the double integral
by using a Riemann sum with
Select the sample points to be the upper right corners of the subsquares of R.
| {: valign=”top”} |
| 10.22 | 10.21 | 9.85 |
| {: valign=”top”} |
| 6.73 | 9.75 | 9.63 |
| {: valign=”top”} |
| 5.62 | 7.83 | 8.21 | {: valign=”top”}{: .unnumbered summary=”This table consists of four columns and four rows. The values along the top row are values of y; specifically, they are y0 = 7, y1 = 8, and y2 = 9. The values down the first column are values of x and they are x0 = 0, x1 = 1, and x2 = 2. Down the second column the values are 10.22, 6.73, and 5.62. Down the third column the values are 10.21, 9.75, and 7.83. Down the fourth column the values are 9.85, 9.63, and 8.21.” data-label=””}
The depth of a children’s 4-ft by 4-ft swimming pool, measured at 1-ft intervals, is given in the following table.
Select the sample points using the midpoint rule on
| y | |||||
| x | 0 | 1 | 2 | 3 | 4 |
| 0 | 1 | 1.5 | 2 | 2.5 | 3 |
| 1 | 1 | 1.5 | 2 | 2.5 | 3 |
| 2 | 1 | 1.5 | 1.5 | 2.5 | 3 |
| 3 | 1 | 1 | 1.5 | 2 | 2.5 |
| 4 | 1 | 1 | 1 | 1.5 | 2 |
a. 28
b. 1.75 ft.
The depth of a 3-ft by 3-ft hole in the ground, measured at 1-ft intervals, is given in the following table.
and the sample points to be the upper left corners of the subsquares of R.
| y | ||||
| x | 0 | 1 | 2 | 3 |
| 0 | 6 | 6.5 | 6.4 | 6 |
| 1 | 6.5 | 7 | 7.5 | 6.5 |
| 2 | 6.5 | 6.7 | 6.5 | 6 |
| 3 | 6 | 6.5 | 5 | 5.6 |
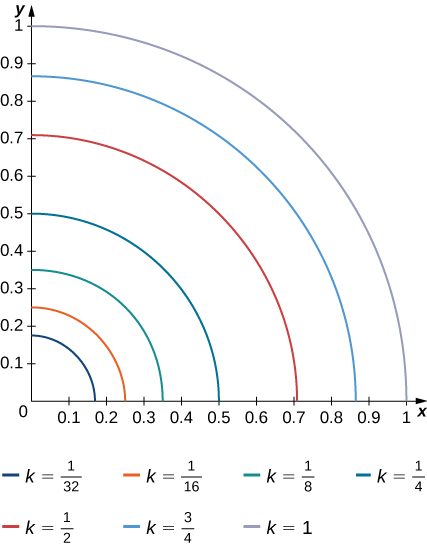
The level curves
of the function f are given in the following graph, where k is a constant.
to estimate the double integral
where
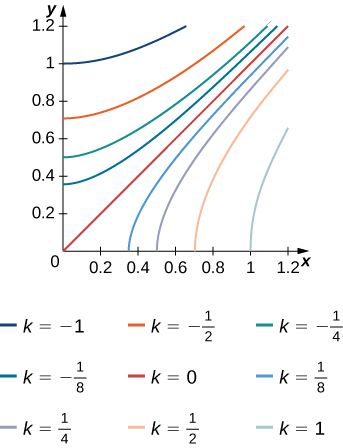
a.
b.
here
and
The level curves
of the function f are given in the following graph, where k is a constant.
to estimate the double integral
where
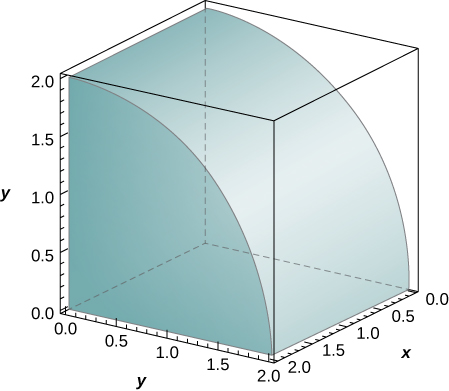
The solid lying under the surface
and above the rectangular region
is illustrated in the following graph. Evaluate the double integral
where
by finding the volume of the corresponding solid.
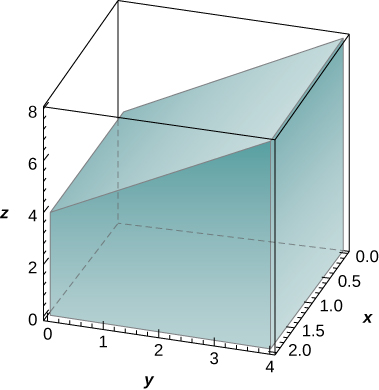
The solid lying under the plane
and above the rectangular region
is illustrated in the following graph. Evaluate the double integral
where
by finding the volume of the corresponding solid.
In the following exercises, calculate the integrals by interchanging the order of integration.
40.
In the following exercises, evaluate the iterated integrals by choosing the order of integration.
0.
In the following exercises, find the average value of the function over the given rectangles.
Let f and g be two continuous functions such that
for any
and
for any
Show that the following inequality is true:
In the following exercises, use property v. of double integrals and the answer from the preceding exercise to show that the following inequalities are true.
where
where
where
where
Let f and g be two continuous functions such that
for any
and
for any
Show that the following inequality is true:
In the following exercises, use property v. of double integrals and the answer from the preceding exercise to show that the following inequalities are true.
where
where
where
where
In the following exercises, the function f is given in terms of double integrals.
and above the region R.
and
in the same system of coordinates.
[T]
where
a.
b.
c.
d.* * *
[T]
where
Show that if f and g are continuous on
and
respectively, then
Show that
[T] Consider the function
where
to estimate the double integral
Round your answers to the nearest hundredths.
find the average value of f over the region R. Round your answer to the nearest hundredths.
and the plane
a. For
b.
c.* * *
[T] Consider the function
where
to estimate the double integral
Round your answers to the nearest hundredths.
find the average value of f over the region R. Round your answer to the nearest hundredths.
and the plane
In the following exercises, the functions
are given, where
is a natural number.
under the surfaces
and above the region R.
as n increases without bound.
a.
b.
Show that the average value of a function f on a rectangular region
is
where
are the sample points of the partition of R, where
and
Use the midpoint rule with
to show that the average value of a function f on a rectangular region
is approximated by
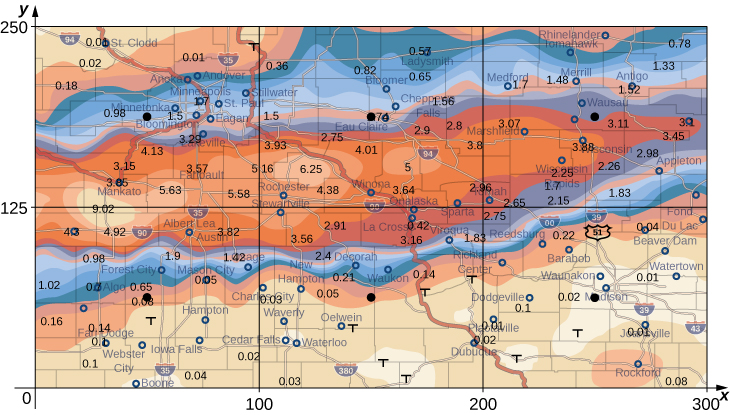
An isotherm map is a chart connecting points having the same temperature at a given time for a given period of time. Use the preceding exercise and apply the midpoint rule with
to find the average temperature over the region given in the following figure.
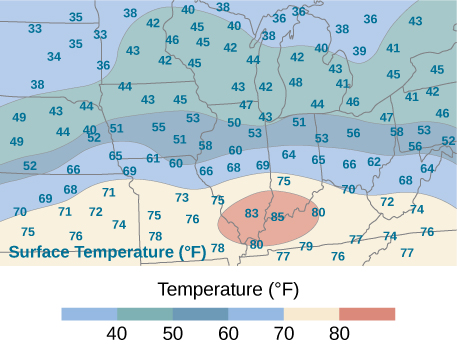
F; here
where
and
are the midpoints of the subintervals of the partitions of
and
respectively.
over the region
in the
-plane is defined as the limit of a double Riemann sum,
over a rectangular region
is
where
is divided into smaller subrectangles
and
is an arbitrary point in
is a function of two variables that is continuous over a rectangular region
then the double integral of
over the region equals an iterated integral,
over the region
is
where
and
are any real numbers and

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: