Solving optimization problems for functions of two or more variables can be similar to solving such problems in single-variable calculus. However, techniques for dealing with multiple variables allow us to solve more varied optimization problems for which we need to deal with additional conditions or constraints. In this section, we examine one of the more common and useful methods for solving optimization problems with constraints.
[link] was an applied situation involving maximizing a profit function, subject to certain constraints. In that example, the constraints involved a maximum number of golf balls that could be produced and sold in
month
and a maximum number of advertising hours that could be purchased per month
Suppose these were combined into a budgetary constraint, such as
that took into account the cost of producing the golf balls and the number of advertising hours purchased per month. The goal is, still, to maximize profit, but now there is a different type of constraint on the values of
and
This constraint, when combined with the profit function
is an example of an optimization problem, and the function
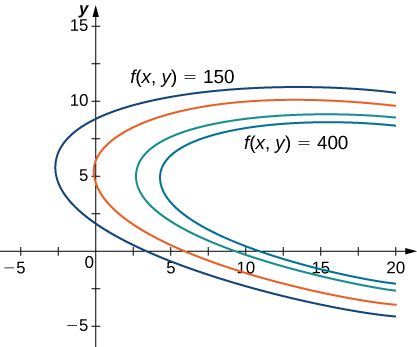
is called the objective function. A graph of various level curves of the function
follows.

In [link], the value
represents different profit levels (i.e., values of the function
As the value of
increases, the curve shifts to the right. Since our goal is to maximize profit, we want to choose a curve as far to the right as possible. If there was no restriction on the number of golf balls the company could produce, or the number of units of advertising available, then we could produce as many golf balls as we want, and advertise as much as we want, and there would be not be a maximum profit for the company. Unfortunately, we have a budgetary constraint that is modeled by the inequality
To see how this constraint interacts with the profit function, [link] shows the graph of the line
superimposed on the previous graph.
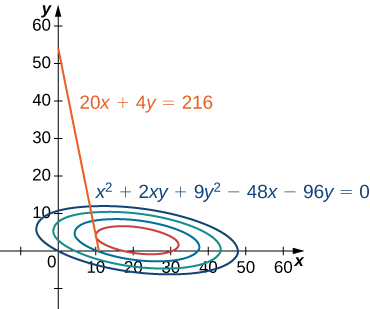
As mentioned previously, the maximum profit occurs when the level curve is as far to the right as possible. However, the level of production corresponding to this maximum profit must also satisfy the budgetary constraint, so the point at which this profit occurs must also lie on (or to the left of) the red line in [link]. Inspection of this graph reveals that this point exists where the line is tangent to the level curve of
Trial and error reveals that this profit level seems to be around
when
and
are both just less than
We return to the solution of this problem later in this section. From a theoretical standpoint, at the point where the profit curve is tangent to the constraint line, the gradient of both of the functions evaluated at that point must point in the same (or opposite) direction. Recall that the gradient of a function of more than one variable is a vector. If two vectors point in the same (or opposite) directions, then one must be a constant multiple of the other. This idea is the basis of the method of Lagrange multipliers.
Let
and
be functions of two variables with continuous partial derivatives at every point of some open set containing the smooth curve
Suppose that
when restricted to points on the curve
has a local extremum at the point
and that
Then there is a number
called a Lagrange multiplier, for which
Assume that a constrained extremum occurs at the point
Furthermore, we assume that the equation
can be smoothly parameterized as
where s is an arc length parameter with reference point
at
Therefore, the quantity
has a relative maximum or relative minimum at
and this implies that
at that point. From the chain rule,
where the derivatives are all evaluated at
However, the first factor in the dot product is the gradient of
and the second factor is the unit tangent vector
to the constraint curve. Since the point
corresponds to
it follows from this equation that
which implies that the gradient is either
or is normal to the constraint curve at a constrained relative extremum. However, the constraint curve
is a level curve for the function
so that if
then
is normal to this curve at
It follows, then, that there is some scalar
such that
□
To apply [link] to an optimization problem similar to that for the golf ball manufacturer, we need a problem-solving strategy.
and the constraint function
Does the optimization problem involve maximizing or minimizing the objective function?
and
at the solutions found in step
maximizes
the smallest of those values minimizes
Use the method of Lagrange multipliers to find the minimum value of
subject to the constraint
Let’s follow the problem-solving strategy:
To determine the constraint function, we must first subtract
from both sides of the constraint. This gives
The constraint function is equal to the left-hand side, so
The problem asks us to solve for the minimum value of
subject to the constraint (see the following graph).
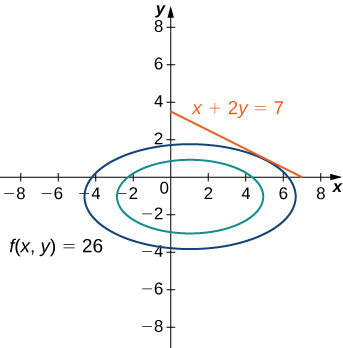
The equation
becomes
which can be rewritten as
Next, we set the coefficients of
equal to each other:
The equation
becomes
Therefore, the system of equations that needs to be solved is
and substituting it into the first equation. This gives
so substituting this into the first equation gives
Solving this equation for
gives
We then substitute this into the third equation:
Since
this gives
into
gives
To ensure this corresponds to a minimum value on the constraint function, let’s try some other values, such as the intercepts of
Which are
and
We get
and
so it appears
has a minimum at
Use the method of Lagrange multipliers to find the maximum value of
subject to the constraint
has a maximum value of
at the point
Use the problem-solving strategy for the method of Lagrange multipliers.
Let’s now return to the problem posed at the beginning of the section.
The golf ball manufacturer, Pro-T, has developed a profit model that depends on the number
of golf balls sold per month (measured in thousands), and the number of hours per month of advertising y, according to the function
where
is measured in thousands of dollars. The budgetary constraint function relating the cost of the production of thousands golf balls and advertising units is given by
Find the values of
and
that maximize profit, and find the maximum profit.
Again, we follow the problem-solving strategy:
To determine the constraint function, we first subtract 216 from both sides of the constraint, then divide both sides by
which gives
The constraint function is equal to the left-hand side, so
The problem asks us to solve for the maximum value of
subject to this constraint.
The equation
becomes
which can be rewritten as
We then set the coefficients of
equal to each other:
The equation
becomes
Therefore, the system of equations that needs to be solved is
in the first equation:
Then we substitute this into the third equation:
Since
this gives
into
which gives
Therefore the maximum profit that can be attained, subject to budgetary constraints, is
with a production level of
golf balls and
hours of advertising bought per month. Let’s check to make sure this truly is a maximum. The endpoints of the line that defines the constraint are
and
Let’s evaluate
at both of these points:
The second value represents a loss, since no golf balls are produced. Neither of these values exceed
so it seems that our extremum is a maximum value of
A company has determined that its production level is given by the Cobb-Douglas function
where x represents the total number of labor hours in
year and y represents the total capital input for the company. Suppose
unit of labor costs
and
unit of capital costs
Use the method of Lagrange multipliers to find the maximum value of
subject to a budgetary constraint of
per year.
A maximum production level of
occurs with
labor hours and
of total capital input.
Use the problem-solving strategy for the method of Lagrange multipliers.
In the case of an optimization function with three variables and a single constraint function, it is possible to use the method of Lagrange multipliers to solve an optimization problem as well. An example of an optimization function with three variables could be the Cobb-Douglas function in the previous example:
where
represents the cost of labor,
represents capital input, and
represents the cost of advertising. The method is the same as for the method with a function of two variables; the equations to be solved are
Maximize the function
subject to the constraint
To determine the constraint function, we subtract
from each side of the constraint:
which gives the constraint function as
and
This leads to the equations
which can be rewritten in the following form:
on the right-hand side, we know that
and all three variables are equal to each other. Substituting
and
into the last equation yields
so
and
and
which corresponds to a critical point on the constraint curve.
Therefore, an extremum of the function is
To verify it is a minimum, choose other points that satisfy the constraint and calculate
at that point. For example,
Both of these values are greater than
leading us to believe the extremum is a minimum.
Use the method of Lagrange multipliers to find the minimum value of the function
subject to the constraint
Use the problem-solving strategy for the method of Lagrange multipliers with an optimization function of three variables.
The method of Lagrange multipliers can be applied to problems with more than one constraint. In this case the optimization function,
is a function of three variables:
and it is subject to two constraints:
There are two Lagrange multipliers,
and
and the system of equations becomes
Find the maximum and minimum values of the function
subject to the constraints
and
Let’s follow the problem-solving strategy:
To determine the constraint functions, we first subtract
from both sides of the first constraint, which gives
so
The second constraint function is
The equation
becomes
which can be rewritten as
Next, we set the coefficients of
equal to each other:
The two equations that arise from the constraints are
and
Combining these equations with the previous three equations gives
Solving the third equation for
and replacing into the first and second equations reduces the number of equations to four:
Next, we solve the first and second equation for
The first equation gives
the second equation gives
We set the right-hand side of each equation equal to each other and cross-multiply:
Therefore, either
or
If
then the first constraint becomes
The only real solution to this equation is
and
which gives the ordered triple
This point does not satisfy the second constraint, so it is not a solution.
Next, we consider
which reduces the number of equations to three:
We substitute the first equation into the second and third equations:
Then, we solve the second equation for
which gives
We then substitute this into the first equation,
and use the quadratic formula to solve for
Recall
so this solves for
as well. Then,
so
Therefore, there are two ordered triplet solutions:
into
which gives
Then, we substitute
into
which gives
is the maximum value and
is the minimum value of
subject to the given constraints.
Use the method of Lagrange multipliers to find the minimum value of the function
subject to the constraints
and
is a minimum.
Use the problem-solving strategy for the method of Lagrange multipliers with two constraints.
For the following exercises, use the method of Lagrange multipliers to find the maximum and minimum values of the function subject to the given constraints.
maximum:
minimum:
maximum:
minimum:
maximum:
minimum =
maxima:
minima:
maximum:
at
minimum:
at
Minimize
on the hyperbola
Minimize
on the ellipse
Maximize
on the sphere
Maximize
The curve
is asymptotic to the line
Find the point(s) on the curve
farthest from the line
Maximize
Minimize
Maximize
Minimize
Minimize
subject to the constraint
Minimize
when
and
minimum:
For the next group of exercises, use the method of Lagrange multipliers to solve the following applied problems.
A pentagon is formed by placing an isosceles triangle on a rectangle, as shown in the diagram. If the perimeter of the pentagon is
in., find the lengths of the sides of the pentagon that will maximize the area of the pentagon.
A rectangular box without a top (a topless box) is to be made from
ft2 of cardboard. Find the maximum volume of such a box.
The maximum volume is
ft3. The dimensions are
ft.
Find the minimum and maximum distances between the ellipse
and the origin.
Find the point on the surface
closest to the point
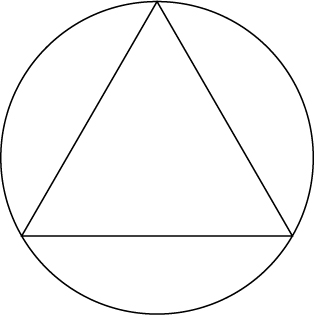
Show that, of all the triangles inscribed in a circle of radius
(see diagram), the equilateral triangle has the largest perimeter.
Find the minimum distance from point
to the parabola
Find the minimum distance from the parabola
to point
Find the minimum distance from the plane
to point
A large container in the shape of a rectangular solid must have a volume of
m3. The bottom of the container costs $5/m2 to construct whereas the top and sides cost $3/m2 to construct. Use Lagrange multipliers to find the dimensions of the container of this size that has the minimum cost.
Find the point on the line
that is closest to point
Find the point on the plane
that is closest to the point
Find the maximum value of
where
denote the acute angles of a right triangle. Draw the contours of the function using a CAS.
A rectangular solid is contained within a tetrahedron with vertices at
and the origin. The base of the box has dimensions
and the height of the box is
If the sum of
is 1.0, find the dimensions that maximizes the volume of the rectangular solid.
[T] By investing x units of labor and y units of capital, a watch manufacturer can produce
watches. Find the maximum number of watches that can be produced on a budget of
if labor costs $100/unit and capital costs $200/unit. Use a CAS to sketch a contour plot of the function.
Roughly 3365 watches at the critical point
For the following exercises, determine whether the statement is true or false. Justify your answer with a proof or a counterexample.
The domain of
is
all real numbers, and
If the function
is continuous everywhere, then
True, by Clairaut’s theorem
The linear approximation to the function of
at
is given by
is a critical point of
False
For the following exercises, sketch the function in one graph and, in a second, sketch several level curves.
Answers may vary
For the following exercises, evaluate the following limits, if they exist. If they do not exist, prove it.
Does not exist
For the following exercises, find the largest interval of continuity for the function.
Continuous at all points on the
except where
For the following exercises, find all first partial derivatives.
For the following exercises, find all second partial derivatives.
For the following exercises, find the equation of the tangent plane to the specified surface at the given point.
at point
at point
Approximate
at
Write down your linear approximation function
How accurate is the approximation to the exact answer, rounded to four digits?
Find the differential
of
and approximate
at the point
Let
and
Find the directional derivative of
in the direction
Find the maximal directional derivative magnitude and direction for the function
at point
For the following exercises, find the gradient.
For the following exercises, find and classify the critical points.
For the following exercises, use Lagrange multipliers to find the maximum and minimum values for the functions with the given constraints.
maximum:
minimum:
A machinist is constructing a right circular cone out of a block of aluminum. The machine gives an error of
in height and
in radius. Find the maximum error in the volume of the cone if the machinist creates a cone of height
cm and radius
cm.
cm3
A trash compactor is in the shape of a cuboid. Assume the trash compactor is filled with incompressible liquid. The length and width are decreasing at rates of
ft/sec and
ft/sec, respectively. Find the rate at which the liquid level is rising when the length is
ft, the width is
ft, and the height is
ft.

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: