Maxima/Minima Problems

Use partial derivatives to locate critical points for a function of two variables.
Apply a second derivative test to identify a critical point as a local maximum, local minimum, or saddle point for a function of two variables.
Examine critical points and boundary points to find absolute maximum and minimum values for a function of two variables.

One of the most useful applications for derivatives of a function of one variable is the determination of maximum and/or minimum values. This application is also important for functions of two or more variables, but as we have seen in earlier sections of this chapter, the introduction of more independent variables leads to more possible outcomes for the calculations. The main ideas of finding critical points and using derivative tests are still valid, but new wrinkles appear when assessing the results.

Critical Points

For functions of a single variable, we defined critical points as the values of the function when the derivative equals zero or does not exist. For functions of two or more variables, the concept is essentially the same, except for the fact that we are now working with partial derivatives.

Definition

Let $z = f (x, y)$

be a function of two variables that is defined on an open set containing the point $(x_{0}, y_{0}) .$

The point $(x_{0}, y_{0})$

is called a critical point of a function of two variables $f$

if one of the two following conditions holds:

$f_{x} (x_{0}, y_{0}) = f_{y} (x_{0}, y_{0}) = 0$
Either $f_{x} (x_{0}, y_{0}) or f_{y} (x_{0}, y_{0})$
does not exist.

Finding Critical Points

Find the critical points of each of the following functions:

$f (x, y) = \sqrt{4 y^{2} - 9 x^{2} + 24 y + 36 x + 36}$
$g (x, y) = x^{2} + 2 x y - 4 y^{2} + 4 x - 6 y + 4$

First, we calculate $f_{x} (x, y) and f_{y} (x, y) :$

$\begin{matrix} f_{x} (x, y) & = & \frac{1}{2} (−18 x + 36) {(4 y^{2} - 9 x^{2} + 24 y + 36 x + 36)}^{−1 / 2} \\ = & \frac{−9 x + 18}{\sqrt{4 y^{2} - 9 x^{2} + 24 y + 36 x + 36}} \\ f_{y} (x, y) & = & \frac{1}{2} (8 y + 24) {(4 y^{2} - 9 x^{2} + 24 y + 36 x + 36)}^{−1 / 2} \\ = & \frac{4 y + 12}{\sqrt{4 y^{2} - 9 x^{2} + 24 y + 36 x + 36}} . \end{matrix}$

Next, we set each of these expressions equal to zero:

$\begin{matrix} \frac{−9 x + 18}{\sqrt{4 y^{2} - 9 x^{2} + 24 y + 36 x + 36}} & = & 0 \\ \frac{4 y + 12}{\sqrt{4 y^{2} - 9 x^{2} + 24 y + 36 x + 36}} & = & 0 . \end{matrix}$

Then, multiply each equation by its common denominator:

$\begin{matrix} - 9 x + 18 & = & 0 \\ 4 y + 12 & = & 0 . \end{matrix}$

Therefore,
$x = 2$
and
$y = −3,$
so
$(2, −3)$
is a critical point of
$f .$

We must also check for the possibility that the denominator of each partial derivative can equal zero, thus causing the partial derivative not to exist. Since the denominator is the same in each partial derivative, we need only do this once:

$4 y^{2} - 9 x^{2} + 24 y + 36 x + 36 = 0 .$

This equation represents a hyperbola. We should also note that the domain of
$f$
consists of points satisfying the inequality

$4 y^{2} - 9 x^{2} + 24 y + 36 x + 36 \geq 0 .$

Therefore, any points on the hyperbola are not only critical points, they are also on the boundary of the domain. To put the hyperbola in standard form, we use the method of completing the square:

$\begin{matrix} 4 y^{2} - 9 x^{2} + 24 y + 36 x + 36 & = & 0 \\ 4 y^{2} - 9 x^{2} + 24 y + 36 x & = & −36 \\ 4 y^{2} + 24 y - 9 x^{2} + 36 x & = & −36 \\ 4 (y^{2} + 6 y) - 9 (x^{2} - 4 x) & = & −36 \\ 4 (y^{2} + 6 y + 9) - 9 (x^{2} - 4 x + 4) & = & −36 + 36 - 36 \\ 4 {(y + 3)}^{2} - 9 {(x - 2)}^{2} & = & −36 . \end{matrix}$

Dividing both sides by
$−36$
puts the equation in standard form:

$\begin{matrix} \frac{4 {(y + 3)}^{2}}{−36} - \frac{9 {(x - 2)}^{2}}{−36} & = & 1 \\ \frac{{(x - 2)}^{2}}{4} - \frac{{(y + 3)}^{2}}{9} & = & 1 . \end{matrix}$

Notice that point
$(2, −3)$
is the center of the hyperbola.
First, we calculate $g_{x} (x, y) and g_{y} (x, y) :$

$\begin{matrix} g_{x} (x, y) & = & 2 x + 2 y + 4 \\ g_{y} (x, y) & = & 2 x - 8 y - 6 . \end{matrix}$

Next, we set each of these expressions equal to zero, which gives a system of equations in
$x and y :$

$\begin{matrix} 2 x + 2 y + 4 & = & 0 \\ 2 x - 8 y - 6 & = & 0 . \end{matrix}$

Subtracting the second equation from the first gives
$10 y + 10 = 0, so y = −1 .$
Substituting this into the first equation gives
$2 x + 2 (−1) + 4 = 0,$
so
$x = −1 .$
Therefore
$(−1, −1)$
is a critical point of
$g$
([link]). There are no points in
$ℝ^{2}$
that make either partial derivative not exist.

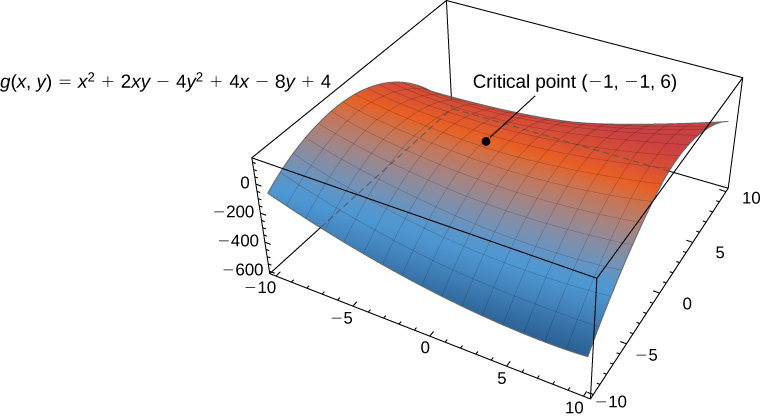
Find the critical point of the function $f (x, y) = x^{3} + 2 x y - 2 x - 4 y .$

(2, −5)

Hint

Calculate $f_{x} (x, y)$

and $f_{y} (x, y),$

then set them equal to zero.

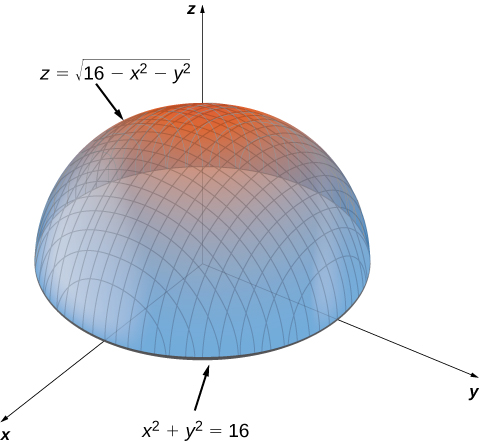
The main purpose for determining critical points is to locate relative maxima and minima, as in single-variable calculus. When working with a function of one variable, the definition of a local extremum involves finding an interval around the critical point such that the function value is either greater than or less than all the other function values in that interval. When working with a function of two or more variables, we work with an open disk around the point.

Definition

Let $z = f (x, y)$

be a function of two variables that is defined and continuous on an open set containing the point $(x_{0}, y_{0}) .$

Then f has a local maximum at $(x_{0}, y_{0})$

f (x_{0}, y_{0}) \geq f (x, y)

for all points $(x, y)$

within some disk centered at $(x_{0}, y_{0}) .$

The number $f (x_{0}, y_{0})$

is called a local maximum value. If the preceding inequality holds for every point $(x, y)$

in the domain of $f,$

then $f$

has a global maximum (also called an absolute maximum) at $(x_{0}, y_{0}) .$

The function $f$

has a local minimum at $(x_{0}, y_{0})$

f (x_{0}, y_{0}) \leq f (x, y)

for all points $(x, y)$

within some disk centered at $(x_{0}, y_{0}) .$

The number $f (x_{0}, y_{0})$

is called a local minimum value. If the preceding inequality holds for every point $(x, y)$

in the domain of $f,$

then $f$

has a global minimum (also called an absolute minimum) at $(x_{0}, y_{0}) .$

If $f (x_{0}, y_{0})$

is either a local maximum or local minimum value, then it is called a local extremum (see the following figure).

The function z = the square root of (16 – x2 – y2) is shown, which is the upper hemisphere of radius 4 with center at the origin. In the xy plane, the circle with radius 4 and center at the origin is highlighted; it has equation x2 + y2 = 16.

In Maxima and Minima, we showed that extrema of functions of one variable occur at critical points. The same is true for functions of more than one variable, as stated in the following theorem.

Fermat’s Theorem for Functions of Two Variables

Let $z = f (x, y)$

be a function of two variables that is defined and continuous on an open set containing the point $(x_{0}, y_{0}) .$

Suppose $f_{x}$

and $f_{y}$

each exists at $(x_{0}, y_{0}) .$

If $f$

has a local extremum at $(x_{0}, y_{0}),$

then $(x_{0}, y_{0})$

is a critical point of $f .$

Second Derivative Test

Consider the function $f (x) = x^{3} .$

This function has a critical point at $x = 0,$

since $f' (0) = 3 {(0)}^{2} = 0 .$

However, $f$

does not have an extreme value at $x = 0 .$

Therefore, the existence of a critical value at $x = x_{0}$

does not guarantee a local extremum at $x = x_{0} .$

The same is true for a function of two or more variables. One way this can happen is at a saddle point. An example of a saddle point appears in the following figure.

The function z = x2 – y2 is shown, which is roughly saddle looking, with the function achieving maxima along the x and y axes.

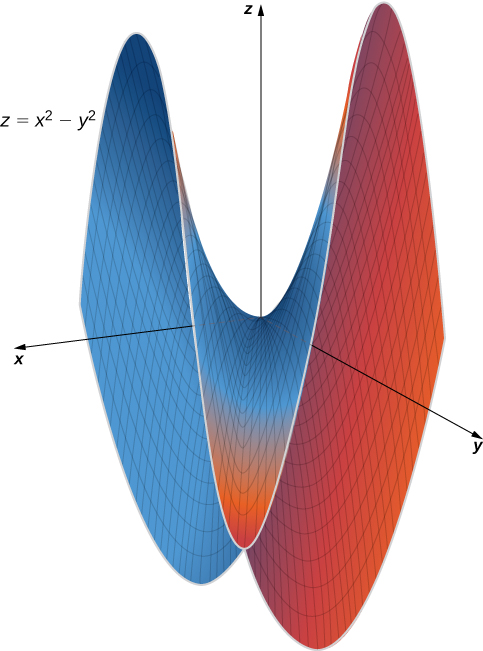
In this graph, the origin is a saddle point. This is because the first partial derivatives of $f (x, y) = x^{2} - y^{2}$

are both equal to zero at this point, but it is neither a maximum nor a minimum for the function. Furthermore the vertical trace corresponding to $y = 0$

is $z = x^{2}$

(a parabola opening upward), but the vertical trace corresponding to $x = 0$

is $z = − y^{2}$

(a parabola opening downward). Therefore, it is both a global maximum for one trace and a global minimum for another.

Definition

Given the function $z = f (x, y),$

the point $(x_{0}, y_{0}, f (x_{0}, y_{0}))$

is a saddle point if both $f_{0} (x_{0}, y_{0}) = 0$

and $f_{y} (x_{0}, y_{0}) = 0,$

but $f$

does not have a local extremum at $(x_{0}, y_{0}) .$

The second derivative test for a function of one variable provides a method for determining whether an extremum occurs at a critical point of a function. When extending this result to a function of two variables, an issue arises related to the fact that there are, in fact, four different second-order partial derivatives, although equality of mixed partials reduces this to three. The second derivative test for a function of two variables, stated in the following theorem, uses a discriminant $D$

that replaces $f ″ (x_{0})$

in the second derivative test for a function of one variable.

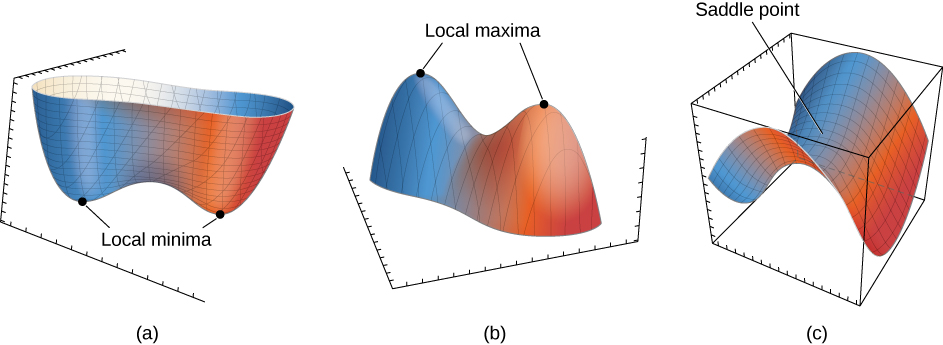
Second Derivative Test

Let $z = f (x, y)$

be a function of two variables for which the first- and second-order partial derivatives are continuous on some disk containing the point $(x_{0}, y_{0}) .$

Suppose $f_{x} (x_{0}, y_{0}) = 0$

and $f_{y} (x_{0}, y_{0}) = 0 .$

Define the quantity

D = f_{x x} (x_{0}, y_{0}) f_{y y} (x_{0}, y_{0}) - {(f_{x y} (x_{0}, y_{0}))}^{2} .

If $D > 0$
and
$f_{x x} (x_{0}, y_{0}) > 0,$
then
$f$
has a local minimum at
$(x_{0}, y_{0}) .$
If $D > 0$
and
$f_{x x} (x_{0}, y_{0}) < 0,$
then
$f$
has a local maximum at
$(x_{0}, y_{0}) .$
If $D < 0,,$
then
$f$
has a saddle point at
$(x_{0}, y_{0}) .$
If $D = 0,$
then the test is inconclusive.

See [link].

This figure consists of three figures labeled a, b, and c. Figure a has two bulbous mounds pointing down, and the two extrema are listed as the local minima. Figure b has two bulbous mounds pointed up, and the two extrema are listed as the local maxima. Figure c is shaped like a saddle, and in the middle of the saddle, a point is marked as the saddle point.

To apply the second derivative test, it is necessary that we first find the critical points of the function. There are several steps involved in the entire procedure, which are outlined in a problem-solving strategy.

Problem-Solving Strategy: Using the Second Derivative Test for Functions of Two Variables

Let $z = f (x, y)$

be a function of two variables for which the first- and second-order partial derivatives are continuous on some disk containing the point $(x_{0}, y_{0}) .$

To apply the second derivative test to find local extrema, use the following steps:

Determine the critical points $(x_{0}, y_{0})$
of the function
$f$
where
$f_{x} (x_{0}, y_{0}) = f_{y} (x_{0}, y_{0}) = 0 .$
Discard any points where at least one of the partial derivatives does not exist.
Calculate the discriminant $D = f_{x x} (x_{0}, y_{0}) f_{y y} (x_{0}, y_{0}) - {(f_{x y} (x_{0}, y_{0}))}^{2}$
for each critical point of
$f .$
Apply [link] to determine whether each critical point is a local maximum, local minimum, or saddle point, or whether the theorem is inconclusive.

Using the Second Derivative Test

Find the critical points for each of the following functions, and use the second derivative test to find the local extrema:

$f (x, y) = 4 x^{2} + 9 y^{2} + 8 x - 36 y + 24$
$g (x, y) = \frac{1}{3} x^{3} + y^{2} + 2 x y - 6 x - 3 y + 4$

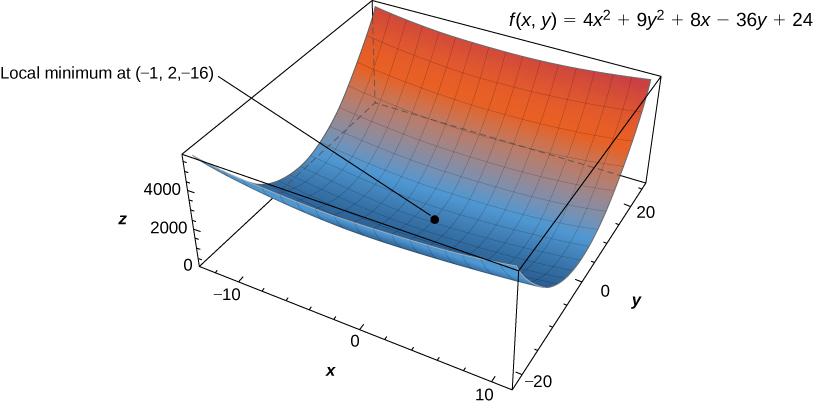
Step $1$
of the problem-solving strategy involves finding the critical points of
$f .$
To do this, we first calculate
$f_{x} (x, y)$
and
$f_{y} (x, y),$
then set each of them equal to zero:

$\begin{matrix} f_{x} (x, y) & = & 8 x + 8 \\ f_{y} (x, y) & = & 18 y - 36 . \end{matrix}$

Setting them equal to zero yields the system of equations

$\begin{matrix} 8 x + 8 & = & 0 \\ 18 y - 36 & = & 0 . \end{matrix}$

The solution to this system is
$x = −1$
and
$y = 2 .$
Therefore
$(−1, 2)$
is a critical point of
$f .$

Step 2 of the problem-solving strategy involves calculating
$D .$
To do this, we first calculate the second partial derivatives of
$f :$

$\begin{matrix} f_{x x} (x, y) & = & 8 \\ f_{x y} (x, y) & = & 0 \\ f_{y y} (x, y) & = & 18 . \end{matrix}$

Therefore,
$D = f_{x x} (−1, 2) f_{y y} (−1, 2) - {(f_{x y} (−1, 2))}^{2} = (8) (18) - {(0)}^{2} = 144 .$

Step 3 states to check [link]. Since
$D > 0$
and
$f_{x x} (−1, 2) > 0,$
this corresponds to case 1. Therefore,
$f$
has a local minimum at
$(−1, 2)$
as shown in the following figure.
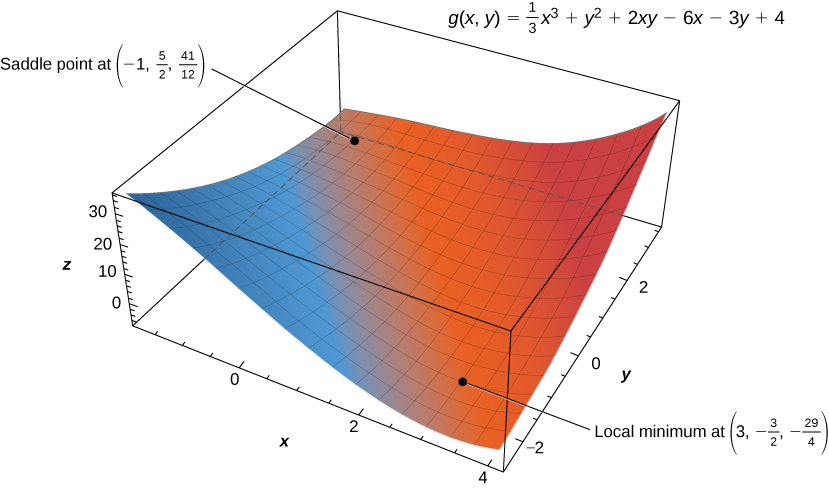
For step 1, we first calculate $g_{x} (x, y)$
and
$g_{y} (x, y),$
then set each of them equal to zero:

$\begin{array}{r} g_{x} (x, y) & = & x^{2} + 2 y - 6 \\ g_{y} (x, y) & = & 2 y + 2 x - 3 . \end{array}$

Setting them equal to zero yields the system of equations

$\begin{matrix} x^{2} + 2 y - 6 & = & 0 \\ 2 y + 2 x - 3 & = & 0 . \end{matrix}$

To solve this system, first solve the second equation for y. This gives
$y = \frac{3 - 2 x}{2} .$
Substituting this into the first equation gives

$\begin{matrix} x^{2} + 3 - 2 x - 6 & = & 0 \\ x^{2} - 2 x - 3 & = & 0 \\ (x - 3) (x + 1) & = & 0 . \end{matrix}$

Therefore, $x = −1$

or $x = 3 .$

Substituting these values into the equation $y = \frac{3 - 2 x}{2}$

yields the critical points $(−1, \frac{5}{2})$

and $(3, - \frac{3}{2}) .$

Step 2 involves calculating the second partial derivatives of $g :$

$\begin{matrix} g_{x x} (x, y) & = & 2 x \\ g_{x y} (x, y) & = & 2 \\ g_{y y} (x, y) & = & 2 . \end{matrix}$

Then, we find a general formula for
$D :$

$\begin{matrix} D & = g_{x x} (x_{0}, y_{0}) g_{y y} (x_{0}, y_{0}) - {(g_{x y} (x_{0}, y_{0}))}^{2} \\ = (2 x_{0}) (2) - 2^{2} \\ = 4 x_{0} - 4 . \end{matrix}$

Next, we substitute each critical point into this formula:

$\begin{matrix} D (−1, \frac{5}{2}) & = & (2 (−1)) (2) - {(2)}^{2} = −4 - 4 = −8 \\ D (3, - \frac{3}{2}) & = & (2 (3)) (2) - {(2)}^{2} = 12 - 4 = 8 . \end{matrix}$

In step 3, we note that, applying [link] to point
$(−1, \frac{5}{2})$
leads to case
$3,$
which means that
$(−1, \frac{5}{2})$
is a saddle point. Applying the theorem to point
$(3, - \frac{3}{2})$
leads to case 1, which means that
$(3, - \frac{3}{2})$
corresponds to a local minimum as shown in the following figure.

Use the second derivative to find the local extrema of the function

f (x, y) = x^{3} + 2 x y - 6 x - 4 y^{2} .

(\frac{4}{3}, \frac{1}{3})

is a saddle point, $(- \frac{3}{2}, - \frac{3}{8})$

is a local maximum.

Hint

Follow the problem-solving strategy for applying the second derivative test.

Absolute Maxima and Minima

When finding global extrema of functions of one variable on a closed interval, we start by checking the critical values over that interval and then evaluate the function at the endpoints of the interval. When working with a function of two variables, the closed interval is replaced by a closed, bounded set. A set is bounded if all the points in that set can be contained within a ball (or disk) of finite radius. First, we need to find the critical points inside the set and calculate the corresponding critical values. Then, it is necessary to find the maximum and minimum value of the function on the boundary of the set. When we have all these values, the largest function value corresponds to the global maximum and the smallest function value corresponds to the absolute minimum. First, however, we need to be assured that such values exist. The following theorem does this.

Extreme Value Theorem

A continuous function $f (x, y)$

on a closed and bounded set $D$

in the plane attains an absolute maximum value at some point of $D$

and an absolute minimum value at some point of $D .$

Now that we know any continuous function $f$

defined on a closed, bounded set attains its extreme values, we need to know how to find them.

Finding Extreme Values of a Function of Two Variables

Assume $z = f (x, y)$

is a differentiable function of two variables defined on a closed, bounded set $D .$

Then $f$

will attain the absolute maximum value and the absolute minimum value, which are, respectively, the largest and smallest values found among the following:

The values of $f$
at the critical points of
$f$
in
$D .$
The values of $f$
on the boundary of
$D .$

The proof of this theorem is a direct consequence of the extreme value theorem and Fermat’s theorem. In particular, if either extremum is not located on the boundary of $D,$

then it is located at an interior point of $D .$

But an interior point $(x_{0}, y_{0})$

of $D$

that’s an absolute extremum is also a local extremum; hence, $(x_{0}, y_{0})$

is a critical point of $f$

by Fermat’s theorem. Therefore the only possible values for the global extrema of $f$

on $D$

are the extreme values of $f$

on the interior or boundary of $D .$

Problem-Solving Strategy: Finding Absolute Maximum and Minimum Values

Let $z = f (x, y)$

be a continuous function of two variables defined on a closed, bounded set $D,$

and assume $f$

is differentiable on $D .$

To find the absolute maximum and minimum values of $f$

on $D,$

do the following:

Determine the critical points of $f$
in
$D .$
Calculate $f$
at each of these critical points.
Determine the maximum and minimum values of $f$
on the boundary of its domain.
The maximum and minimum values of $f$
will occur at one of the values obtained in steps
$2 and 3 .$

Finding the maximum and minimum values of $f$

on the boundary of $D$

can be challenging. If the boundary is a rectangle or set of straight lines, then it is possible to parameterize the line segments and determine the maxima on each of these segments, as seen in [link]. The same approach can be used for other shapes such as circles and ellipses.

If the boundary of the set $D$

is a more complicated curve defined by a function $g (x, y) = c$

for some constant $c,$

and the first-order partial derivatives of $g$

exist, then the method of Lagrange multipliers can prove useful for determining the extrema of $f$

on the boundary. The method of Lagrange multipliers is introduced in Lagrange Multipliers.

Finding Absolute Extrema

Use the problem-solving strategy for finding absolute extrema of a function to determine the absolute extrema of each of the following functions:

$f (x, y) = x^{2} - 2 x y + 4 y^{2} - 4 x - 2 y + 24$
on the domain defined by
$0 \leq x \leq 4$
and
$0 \leq y \leq 2$
$g (x, y) = x^{2} + y^{2} + 4 x - 6 y$
on the domain defined by
$x^{2} + y^{2} \leq 16$

Using the problem-solving strategy, step $1$
involves finding the critical points of
$f$
on its domain. Therefore, we first calculate
$f_{x} (x, y)$
and
$f_{y} (x, y),$
then set them each equal to zero:

$\begin{matrix} f_{x} (x, y) & = & 2 x - 2 y - 4 \\ f_{y} (x, y) & = & −2 x + 8 y - 2 . \end{matrix}$

Setting them equal to zero yields the system of equations

$\begin{matrix} 2 x - 2 y - 4 & = & 0 \\ - 2 x + 8 y - 2 & = & 0 . \end{matrix}$

The solution to this system is
$x = 3$
and
$y = 1 .$
Therefore
$(3, 1)$
is a critical point of
$f .$
Calculating
$f (3, 1)$
gives
$f (3, 1) = 17 .$

The next step involves finding the extrema of
$f$
on the boundary of its domain. The boundary of its domain consists of four line segments as shown in the following graph:

$L_{1}$
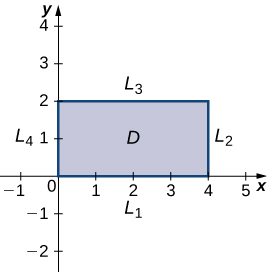
is the line segment connecting
$(0, 0)$
and
$(4, 0),$
and it can be parameterized by the equations
$x (t) = t, y (t) = 0$
for
$0 \leq t \leq 4 .$
Define
$g (t) = f (x (t), y (t)) .$
This gives
$g (t) = t^{2} - 4 t + 24 .$
Differentiating g leads to
$g^{'} (t) = 2 t - 4 .$
Therefore,
$g$
has a critical value at
$t = 2,$
which corresponds to the point
$(2, 0) .$
Calculating
$f (2, 0)$
gives the z-value
$20 .$
$L_{2}$
is the line segment connecting
$(4, 0)$
and
$(4, 2),$
and it can be parameterized by the equations
$x (t) = 4, y (t) = t$
for
$0 \leq t \leq 2 .$
Again, define
$g (t) = f (x (t), y (t)) .$
This gives
$g (t) = 4 t^{2} - 10 t + 24 .$
Then,
$g^{'} (t) = 8 t - 10 .$ $g$
has a critical value at
$t = \frac{5}{4},$
which corresponds to the point
$(0, \frac{5}{4}) .$
Calculating
$f (0, \frac{5}{4})$
gives the z-value
$27.75 .$
$L_{3}$
is the line segment connecting
$(0, 2)$
and
$(4, 2),$
and it can be parameterized by the equations
$x (t) = t, y (t) = 2$
for
$0 \leq t \leq 4 .$
Again, define
$g (t) = f (x (t), y (t)) .$
This gives
$g (t) = t^{2} - 8 t + 36 .$
The critical value

corresponds to the point
$(4, 2) .$
So, calculating
$f (4, 2)$
gives the z-value
$20 .$
$L_{4}$
is the line segment connecting
$(0, 0)$
and
$(0, 2),$
and it can be parameterized by the equations
$x (t) = 0, y (t) = t$
for
$0 \leq t \leq 2 .$
This time,
$g (t) = 4 t^{2} - 2 t + 24$
and the critical value
$t = \frac{1}{4}$
correspond to the point
$(0, \frac{1}{4}) .$
Calculating
$f (0, \frac{1}{4})$
gives the z-value
$23.75 .$

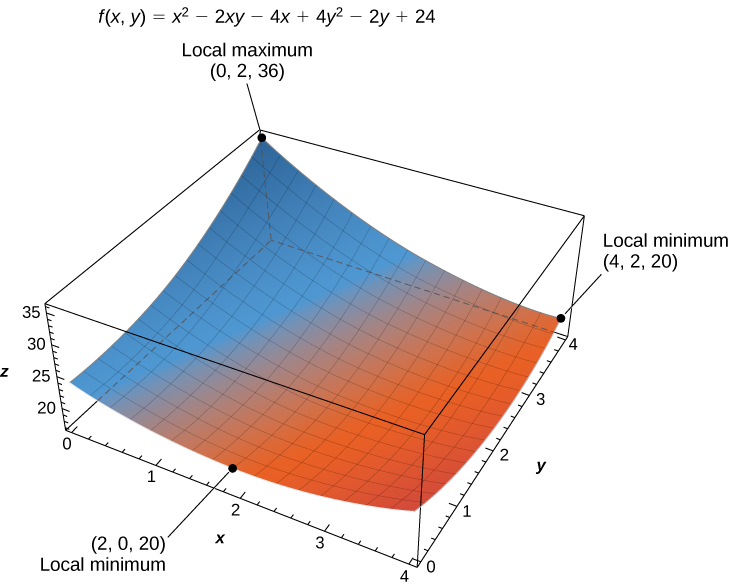
We also need to find the values of
$f (x, y)$
at the corners of its domain. These corners are located at
$(0, 0), (4, 0), (4, 2) and (0, 2) :$

$\begin{matrix} f (0, 0) & = & {(0)}^{2} - 2 (0) (0) + 4 {(0)}^{2} - 4 (0) - 2 (0) + 24 & = & 24 \\ f (4, 0) & = & {(4)}^{2} - 2 (4) (0) + 4 {(0)}^{2} - 4 (4) - 2 (0) + 24 & = & 24 \\ f (4, 2) & = & {(4)}^{2} - 2 (4) (2) + 4 {(2)}^{2} - 4 (4) - 2 (2) + 24 & = & 20 \\ f (0, 2) & = & {(0)}^{2} - 2 (0) (2) + 4 {(2)}^{2} - 4 (0) - 2 (2) + 24 & = & 36 . \end{matrix}$

The absolute maximum value is
$36,$
which occurs at
$(0, 2),$
and the global minimum value is
$20,$
which occurs at both
$(4, 2)$
and
$(2, 0)$
as shown in the following figure.
Using the problem-solving strategy, step $1$
involves finding the critical points of
$g$
on its domain. Therefore, we first calculate
$g_{x} (x, y)$
and
$g_{y} (x, y),$
then set them each equal to zero:

$\begin{matrix} g_{x} (x, y) & = & 2 x + 4 \\ g_{y} (x, y) & = & 2 y - 6 . \end{matrix}$

Setting them equal to zero yields the system of equations

$\begin{matrix} 2 x + 4 & = & 0 \\ 2 y - 6 & = & 0 . \end{matrix}$

The solution to this system is
$x = −2$
and
$y = 3 .$
Therefore,
$(−2, 3)$
is a critical point of
$g .$
Calculating
$g (−2, 3),$
we get

$g (−2, 3) = {(−2)}^{2} + 3^{2} + 4 (−2) - 6 (3) = 4 + 9 - 8 - 18 = −13 .$

The next step involves finding the extrema of g on the boundary of its domain. The boundary of its domain consists of a circle of radius
$4$
centered at the origin as shown in the following graph.

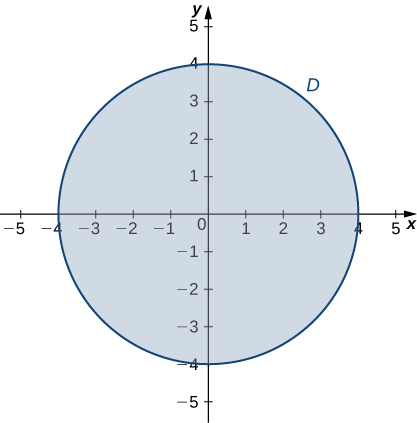
The boundary of the domain of
$g$
can be parameterized using the functions
$x (t) = 4 cos t, y (t) = 4 sin t$
for
$0 \leq t \leq 2 π .$
Define
$h (t) = g (x (t), y (t)) :$

$\begin{matrix} h (t) & = g (x (t), y (t)) \\ = {(4 cos t)}^{2} + {(4 sin t)}^{2} + 4 (4 cos t) - 6 (4 sin t) \\ = 16 {cos}^{2} t + 16 {sin}^{2} t + 16 cos t - 24 sin t \\ = 16 + 16 cos t - 24 sin t . \end{matrix}$

Setting
$h^{'} (t) = 0$
leads to

$\begin{matrix} - 16 sin t - 24 cos t & = & 0 \\ - 16 sin t & = & 24 cos t \\ \frac{−16 sin t}{−16 cos t} & = & \frac{24 cos t}{−16 cos t} \\ tan t & = & - \frac{3}{2} . \end{matrix}$

This equation has two solutions over the interval
$0 \leq t \leq 2 π .$
One is
$t = π - arctan (\frac{3}{2})$
and the other is
$t = 2 π - arctan (\frac{3}{2}) .$
For the first angle,

$\begin{matrix} sin t & = & sin (π - arctan (\frac{3}{2})) = sin (arctan (\frac{3}{2})) = \frac{3 \sqrt{13}}{13} \\ cos t & = & cos (π - arctan (\frac{3}{2})) = − cos (arctan (\frac{3}{2})) = - \frac{2 \sqrt{13}}{13} . \end{matrix}$

Therefore,
$x (t) = 4 cos t = - \frac{8 \sqrt{13}}{13}$
and
$y (t) = 4 sin t = \frac{12 \sqrt{13}}{13},$
so
$(- \frac{8 \sqrt{13}}{13}, \frac{12 \sqrt{13}}{13})$
is a critical point on the boundary and

$\begin{matrix} g (- \frac{8 \sqrt{13}}{13}, \frac{12 \sqrt{13}}{13}) & = {(- \frac{8 \sqrt{13}}{13})}^{2} + {(\frac{12 \sqrt{13}}{13})}^{2} + 4 (- \frac{8 \sqrt{13}}{13}) - 6 (\frac{12 \sqrt{13}}{13}) \\ = \frac{144}{13} + \frac{64}{13} - \frac{32 \sqrt{13}}{13} - \frac{72 \sqrt{13}}{13} \\ = \frac{208 - 104 \sqrt{13}}{13} \approx −12.844 . \end{matrix}$

For the second angle,

$\begin{matrix} sin t & = & sin (2 π - arctan (\frac{3}{2})) = − sin (arctan (\frac{3}{2})) = - \frac{3 \sqrt{13}}{13} \\ cos t & = & cos (2 π - arctan (\frac{3}{2})) = cos (arctan (\frac{3}{2})) = \frac{2 \sqrt{13}}{13} . \end{matrix}$

Therefore,
$x (t) = 4 cos t = \frac{8 \sqrt{13}}{13}$
and
$y (t) = 4 sin t = - \frac{12 \sqrt{13}}{13},$
so
$(\frac{8 \sqrt{13}}{13}, - \frac{12 \sqrt{13}}{13})$
is a critical point on the boundary and

$\begin{matrix} g (\frac{8 \sqrt{13}}{13}, - \frac{12 \sqrt{13}}{13}) & = {(\frac{8 \sqrt{13}}{13})}^{2} + {(- \frac{12 \sqrt{13}}{13})}^{2} + 4 (\frac{8 \sqrt{13}}{13}) - 6 (- \frac{12 \sqrt{13}}{13}) \\ = \frac{144}{13} + \frac{64}{13} + \frac{32 \sqrt{13}}{13} + \frac{72 \sqrt{13}}{13} \\ = \frac{208 + 104 \sqrt{13}}{13} \approx 44.844 . \end{matrix}$

The absolute minimum of g is
$−13,$
which is attained at the point
$(−2, 3),$
which is an interior point of D. The absolute maximum of g is approximately equal to 44.844, which is attained at the boundary point
$(\frac{8 \sqrt{13}}{13}, - \frac{12 \sqrt{13}}{13}) .$
These are the absolute extrema of g on D as shown in the following figure.

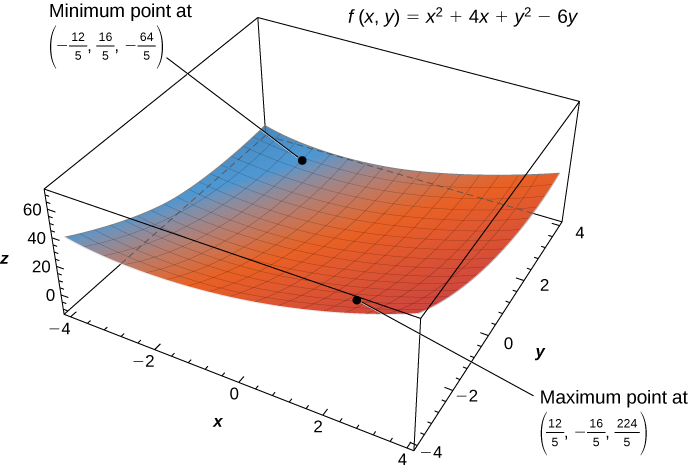
Use the problem-solving strategy for finding absolute extrema of a function to find the absolute extrema of the function

f (x, y) = 4 x^{2} - 2 x y + 6 y^{2} - 8 x + 2 y + 3

on the domain defined by $0 \leq x \leq 2$

and $−1 \leq y \leq 3 .$

The absolute minimum occurs at $(1, 0) :$

f (1, 0) = −1 .

The absolute maximum occurs at $(0, 3) :$

f (0, 3) = 63 .

Hint

Calculate $f_{x} (x, y)$

and $f_{y} (x, y),$

and set them equal to zero. Then, calculate $f$

for each critical point and find the extrema of $f$

on the boundary of $D .$

Chapter Opener: Profitable Golf Balls

A basket full of golf balls.

Pro- $T$

company has developed a profit model that depends on the number x of golf balls sold per month (measured in thousands), and the number of hours per month of advertising y, according to the function

z = f (x, y) = 48 x + 96 y - x^{2} - 2 x y - 9 y^{2},

where $z$

is measured in thousands of dollars. The maximum number of golf balls that can be produced and sold is $50,000,$

and the maximum number of hours of advertising that can be purchased is $25 .$

Find the values of $x$

and $y$

that maximize profit, and find the maximum profit.

Using the problem-solving strategy, step $1$

involves finding the critical points of $f$

on its domain. Therefore, we first calculate $f_{x} (x, y)$

and $f_{y} (x, y),$

then set them each equal to zero:

\begin{matrix} f_{x} (x, y) & = & 48 - 2 x - 2 y \\ f_{y} (x, y) & = & 96 - 2 x - 18 y . \end{matrix}

Setting them equal to zero yields the system of equations

\begin{matrix} 48 - 2 x - 2 y & = & 0 \\ 96 - 2 x - 18 y & = & 0 . \end{matrix}

The solution to this system is $x = 21$

and $y = 3 .$

Therefore $(21, 3)$

is a critical point of $f .$

Calculating $f (21, 3)$

gives $f (21, 3) = 48 (21) + 96 (3) - 21^{2} - 2 (21) (3) - 9 {(3)}^{2} = 648 .$

The domain of this function is $0 \leq x \leq 50$

and $0 \leq y \leq 25$

as shown in the following graph.

A rectangle is drawn in the first quadrant with one corner at the origin, horizontal length 50, and height 25. This rectangle is marked D, and the sides are marked in counterclockwise order from the side overlapping the x axis L1, L2, L3, and L4.

L_{1}

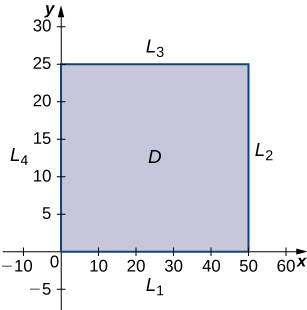
is the line segment connecting $(0, 0)$

and $(50, 0),$

and it can be parameterized by the equations $x (t) = t, y (t) = 0$

for $0 \leq t \leq 50 .$

We then define $g (t) = f (x (t), y (t)) :$

\begin{matrix} g (t) & = f (x (t), y (t)) \\ = f (t, 0) \\ = 48 t + 96 (0) - y^{2} - 2 (t) (0) - 9 {(0)}^{2} \\ = 48 t - t^{2} . \end{matrix}

Setting $g^{'} (t) = 0$

yields the critical point $t = 24,$

which corresponds to the point $(24, 0)$

in the domain of $f .$

Calculating $f (24, 0)$

gives $576 .$

L_{2}

is the line segment connecting

and $(50, 25),$

and it can be parameterized by the equations $x (t) = 50, y (t) = t$

for $0 \leq t \leq 25 .$

Once again, we define $g (t) = f (x (t), y (t)) :$

\begin{matrix} g (t) & = f (x (t), y (t)) \\ = f (50, t) \\ = 48 (50) + 96 t - 50^{2} - 2 (50) t - 9 t^{2} \\ = −9 t^{2} - 4 t - 100 . \end{matrix}

This function has a critical point at $t = - \frac{2}{9},$

which corresponds to the point $(50, - \frac{2}{9}) .$

This point is not in the domain of $f .$

L_{3}

is the line segment connecting $(0, 25) and (50, 25),$

and it can be parameterized by the equations $x (t) = t, y (t) = 25$

for $0 \leq t \leq 50 .$

We define $g (t) = f (x (t), y (t)) :$

\begin{matrix} g (t) & = f (x (t), y (t)) \\ = f (t, 25) \\ = 48 t + 96 (25) - t^{2} - 2 t (25) - 9 (25^{2}) \\ = − t^{2} - 2 t - 3225 . \end{matrix}

This function has a critical point at $t = −1,$

which corresponds to the point $(−1, 25),$

which is not in the domain.

L_{4}

is the line segment connecting $(0, 0) to (0, 25),$

and it can be parameterized by the equations $x (t) = 0, y (t) = t$

for $0 \leq t \leq 25 .$

We define $g (t) = f (x (t), y (t)) :$

\begin{matrix} g (t) & = f (x (t), y (t)) \\ = f (0, t) \\ = 48 (0) + 96 t - {(0)}^{2} - 2 (0) t - 9 t^{2} \\ = 96 t - t^{2} . \end{matrix}

This function has a critical point at $t = \frac{16}{3},$

which corresponds to the point $(0, \frac{16}{3}),$

which is on the boundary of the domain. Calculating $f (0, \frac{16}{3})$

gives $256 .$

We also need to find the values of $f (x, y)$

at the corners of its domain. These corners are located at $(0, 0), (50, 0), (50, 25) and (0, 25) :$

\begin{matrix} f (0, 0) & = & 48 (0) + 96 (0) - {(0)}^{2} - 2 (0) (0) - 9 {(0)}^{2} = 0 \\ f (50, 0) & = & 48 (50) + 96 (0) - {(50)}^{2} - 2 (50) (0) - 9 {(0)}^{2} = −100 \\ f (50, 25) & = & 48 (50) + 96 (25) - {(50)}^{2} - 2 (50) (25) - 9 {(25)}^{2} = −5825 \\ f (0, 25) & = & 48 (0) + 96 (25) - {(0)}^{2} - 2 (0) (25) - 9 {(25)}^{2} = −3225 . \end{matrix}

The maximum critical value is $648,$

which occurs at $(21, 3) .$

Therefore, a maximum profit of $$ 648,000$

is realized when $21,000$

golf balls are sold and $3$

hours of advertising are purchased per month as shown in the following figure.

The function f(x, y) = 48x + 96y – x2 – 2xy – 9y2 is shown with maximum point at (21, 3, 648). The shape is a plane curving from near the origin down to (50, 25).

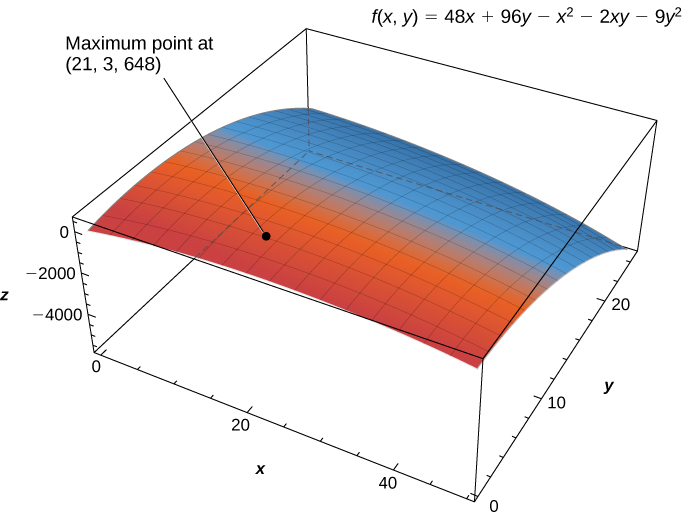
Key Concepts

A critical point of the function $f (x, y)$
is any point
$(x_{0}, y_{0})$
where either
$f_{x} (x_{0}, y_{0}) = f_{y} (x_{0}, y_{0}) = 0,$
or at least one of
$f_{x} (x_{0}, y_{0})$
and
$f_{y} (x_{0}, y_{0})$
do not exist.
A saddle point is a point $(x_{0}, y_{0})$
where
$f_{x} (x_{0}, y_{0}) = f_{y} (x_{0}, y_{0}) = 0,$
but
$(x_{0}, y_{0})$
is neither a maximum nor a minimum at that point.
To find extrema of functions of two variables, first find the critical points, then calculate the discriminant and apply the second derivative test.

Key Equations

Discriminant
$D = f_{x x} (x_{0}, y_{0}) f_{y y} (x_{0}, y_{0}) - {(f_{x y} (x_{0}, y_{0}))}^{2}$

For the following exercises, find all critical points.

f (x, y) = 1 + x^{2} + y^{2}

f (x, y) = {(3 x - 2)}^{2} + {(y - 4)}^{2}

(\frac{2}{3}, 4)

f (x, y) = x^{4} + y^{4} - 16 x y

f (x, y) = 15 x^{3} - 3 x y + 15 y^{3}

(0, 0)

(\frac{1}{15}, \frac{1}{15})

For the following exercises, find the critical points of the function by using algebraic techniques (completing the square) or by examining the form of the equation. Verify your results using the partial derivatives test.

f (x, y) = \sqrt{x^{2} + y^{2} + 1}

f (x, y) = − x^{2} - 5 y^{2} + 8 x - 10 y - 13

Maximum at $(4, −1, 8)$

f (x, y) = x^{2} + y^{2} + 2 x - 6 y + 6

f (x, y) = \sqrt{x^{2} + y^{2}} + 1

Relative minimum at $(0, 0, 1)$

For the following exercises, use the second derivative test to identify any critical points and determine whether each critical point is a maximum, minimum, saddle point, or none of these.

f (x, y) = − x^{3} + 4 x y - 2 y^{2} + 1

f (x, y) = x^{2} y^{2}

The second derivative test fails. Since $x^{2} y^{2} > 0$

for all x and y different from zero, and $x^{2} y^{2} = 0$

when either x or y equals zero (or both), then the absolute minimum occurs at $(0, 0) .$

f (x, y) = x^{2} - 6 x + y^{2} + 4 y - 8

f (x, y) = 2 x y + 3 x + 4 y

f (−2, - \frac{3}{2}) = −6

is a saddle point.

f (x, y) = 8 x y (x + y) + 7

f (x, y) = x^{2} + 4 x y + y^{2}

f (0, 0) = 0;

(0, 0, 0)

is a saddle point.

f (x, y) = x^{3} + y^{3} - 300 x - 75 y - 3

f (x, y) = 9 - x^{4} y^{4}

f (0, 0) = 9

is a local maximum.

f (x, y) = 7 x^{2} y + 9 x y^{2}

f (x, y) = 3 x^{2} - 2 x y + y^{2} - 8 y

Relative minimum located at $(2, 6) .$

f (x, y) = 3 x^{2} + 2 x y + y^{2}

f (x, y) = y^{2} + x y + 3 y + 2 x + 3

(1, −2)

is a saddle point.

f (x, y) = x^{2} + x y + y^{2} - 3 x

f (x, y) = x^{2} + 2 y^{2} - x^{2} y

(2, 1)

and $(−2, 1)$

are saddle points; $(0, 0)$

is a relative minimum.

f (x, y) = x^{2} + y - e^{y}

f (x, y) = e^{− (x^{2} + y^{2} + 2 x)}

(−1, 0)

is a relative maximum.

f (x, y) = x^{2} + x y + y^{2} - x - y + 1

f (x, y) = x^{2} + 10 x y + y^{2}

(0, 0)

is a saddle point.

f (x, y) = − x^{2} - 5 y^{2} + 10 x - 30 y - 62

f (x, y) = 120 x + 120 y - x y - x^{2} - y^{2}

The relative maximum is at $(40, 40) .$

f (x, y) = 2 x^{2} + 2 x y + y^{2} + 2 x - 3

f (x, y) = x^{2} + x - 3 x y + y^{3} - 5

(\frac{1}{4}, \frac{1}{2})

is a saddle point and $(1, 1)$

is the relative minimum.

f (x, y) = 2 x y e^{− x^{2} - y^{2}}

For the following exercises, determine the extreme values and the saddle points. Use a CAS to graph the function.

[T] $f (x, y) = y e^{x} - e^{y}$

A saddle point is located at $(0, 0) .$

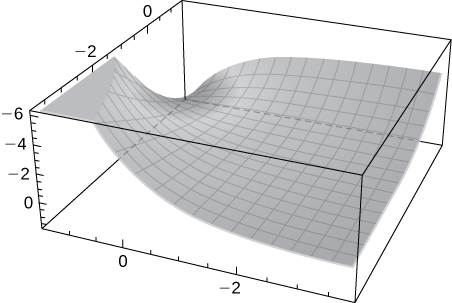
A complicated graph that starts near (1, 1, 1), and decreases significantly along the x and y axes, so much so along the y axis that it is cut off. The rest of the graph stays near 0.

[T] $f (x, y) = x sin (y)$

[T] $f (x, y) = sin (x) sin (y), x \in (0, 2 π), y \in (0, 2 π)$

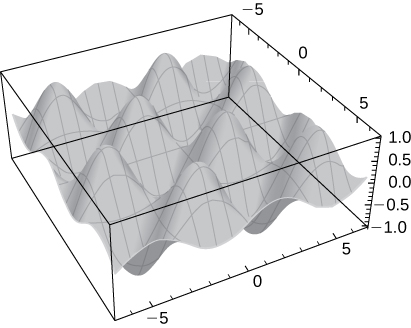
There is a saddle point at $(π, π),$

local maxima at $(\frac{π}{2}, \frac{π}{2}) and (\frac{3 π}{2}, \frac{3 π}{2}),$

and local minima at $(\frac{π}{2}, \frac{3 π}{2}) and (\frac{3 π}{2}, \frac{π}{2}) .$

A series of hills and holes alternating through a space with amplitude 1.

Find the absolute extrema of the given function on the indicated closed and bounded set $R .$

f (x, y) = x y - x - 3 y;

R

is the triangular region with vertices $(0, 0), (0, 4), and (5, 0) .$

Find the absolute maximum and minimum values of $f (x, y) = x^{2} + y^{2} - 2 y + 1$

on the region $R = {(x, y) \| x^{2} + y^{2} \leq 4} .$

(0, 1, 0)

is the absolute minimum and $(0, −2, 9)$

is the absolute maximum.

f (x, y) = x^{3} - 3 x y - y^{3}

on $R = {(x, y) : −2 \leq x \leq 2, −2 \leq y \leq 2}$

f (x, y) = \frac{−2 y}{x^{2} + y^{2} + 1}

on $R = {(x, y) : x^{2} + y^{2} \leq 4}$

There is an absolute minimum at $(0, 1, −1)$

and an absolute maximum at $(0, −1, 1) .$

Find three positive numbers the sum of which is $27,$

such that the sum of their squares is as small as possible.

Find the points on the surface $x^{2} - y z = 5$

that are closest to the origin.

(\sqrt{5}, 0, 0), (− \sqrt{5}, 0, 0)

Find the maximum volume of a rectangular box with three faces in the coordinate planes and a vertex in the first octant on the plane $x + y + z = 1 .$

The sum of the length and the girth (perimeter of a cross-section) of a package carried by a delivery service cannot exceed $108$

in. Find the dimensions of the rectangular package of largest volume that can be sent.

18 by 36 by 18 in .

A cardboard box without a lid is to be made with a volume of $4$

ft³. Find the dimensions of the box that requires the least amount of cardboard.

Find the point on the surface $f (x, y) = x^{2} + y^{2} + 10$

nearest the plane $x + 2 y - z = 0 .$

Identify the point on the plane.

(\frac{47}{24}, \frac{47}{12}, \frac{235}{24})

Find the point in the plane $2 x - y + 2 z = 16$

that is closest to the origin.

A company manufactures two types of athletic shoes: jogging shoes and cross-trainers. The total revenue from $x$

units of jogging shoes and $y$

units of cross-trainers is given by $R (x, y) = −5 x^{2} - 8 y^{2} - 2 x y + 42 x + 102 y,$

where $x$

and $y$

are in thousands of units. Find the values of x and y to maximize the total revenue.

x = 3

and $y = 6$

A shipping company handles rectangular boxes provided the sum of the length, width, and height of the box does not exceed $96$

in. Find the dimensions of the box that meets this condition and has the largest volume.

Find the maximum volume of a cylindrical soda can such that the sum of its height and circumference is $120$

cm.

V = \frac{64,000}{π} \approx 20, 372

cm³

Glossary

critical point of a function of two variables

the point

(x_{0}, y_{0})

is called a critical point of

f (x, y)

if one of the two following conditions holds:

$f_{x} (x_{0}, y_{0}) = f_{y} (x_{0}, y_{0}) = 0$
At least one of $f_{x} (x_{0}, y_{0})$
and
$f_{y} (x_{0}, y_{0})$
do not exist

discriminant: the discriminant of the function $f (x, y)$
is given by the formula
$D = f_{x x} (x_{0}, y_{0}) f_{y y} (x_{0}, y_{0}) - {(f_{x y} (x_{0}, y_{0}))}^{2}$

saddle point

given the function

z = f (x, y),

the point

(x_{0}, y_{0}, f (x_{0}, y_{0}))

is a saddle point if both

f_{x} (x_{0}, y_{0}) = 0

and

f_{y} (x_{0}, y_{0}) = 0,

but

f

does not have a local extremum at

(x_{0}, y_{0})

This work is licensed under a Creative Commons Attribution 4.0 International License.

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1

Attribution:

For questions regarding this license, please contact partners@openstaxcollege.org.
If you use this textbook as a bibliographic reference, then you should cite it as follows: OpenStax College, Calculus. OpenStax CNX. http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1.
If you redistribute this textbook in a print format, then you must include on every physical page the following attribution: "Download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1."
If you redistribute part of this textbook, then you must retain in every digital format page view (including but not limited to EPUB, PDF, and HTML) and on every physical printed page the following attribution: "Download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1."