In single-variable calculus, we found that one of the most useful differentiation rules is the chain rule, which allows us to find the derivative of the composition of two functions. The same thing is true for multivariable calculus, but this time we have to deal with more than one form of the chain rule. In this section, we study extensions of the chain rule and learn how to take derivatives of compositions of functions of more than one variable.
Recall that the chain rule for the derivative of a composite of two functions can be written in the form
In this equation, both
and
are functions of one variable. Now suppose that
is a function of two variables and
is a function of one variable. Or perhaps they are both functions of two variables, or even more. How would we calculate the derivative in these cases? The following theorem gives us the answer for the case of one independent variable.
Suppose that
and
are differentiable functions of
and
is a differentiable function of
Then
is a differentiable function of
and
where the ordinary derivatives are evaluated at
and the partial derivatives are evaluated at
The proof of this theorem uses the definition of differentiability of a function of two variables. Suppose that f is differentiable at the point
where
and
for a fixed value of
We wish to prove that
is differentiable at
and that [link] holds at that point as well.
Since
is differentiable at
we know that
where
We then subtract
from both sides of this equation:
Next, we divide both sides by
Then we take the limit as
approaches
The left-hand side of this equation is equal to
which leads to
The last term can be rewritten as
As
approaches
approaches
so we can rewrite the last product as
Since the first limit is equal to zero, we need only show that the second limit is finite:
Since
and
are both differentiable functions of
both limits inside the last radical exist. Therefore, this value is finite. This proves the chain rule at
the rest of the theorem follows from the assumption that all functions are differentiable over their entire domains.
□
Closer examination of [link] reveals an interesting pattern. The first term in the equation is
and the second term is
Recall that when multiplying fractions, cancelation can be used. If we treat these derivatives as fractions, then each product “simplifies” to something resembling
The variables
that disappear in this simplification are often called intermediate variables: they are independent variables for the function
but are dependent variables for the variable
Two terms appear on the right-hand side of the formula, and
is a function of two variables. This pattern works with functions of more than two variables as well, as we see later in this section.
Calculate
for each of the following functions:
and
Now, we substitute each of these into [link]:
This answer has three variables in it. To reduce it to one variable, use the fact that
We obtain
This derivative can also be calculated by first substituting
and
into
then differentiating with respect to
Then
which is the same solution. However, it may not always be this easy to differentiate in this form.
and
We substitute each of these into [link]:
To reduce this to one variable, we use the fact that
and
Therefore,
To eliminate negative exponents, we multiply the top by
and the bottom by
Again, this derivative can also be calculated by first substituting
and
into
then differentiating with respect to
Then
This is the same solution.
Calculate
given the following functions. Express the final answer in terms of
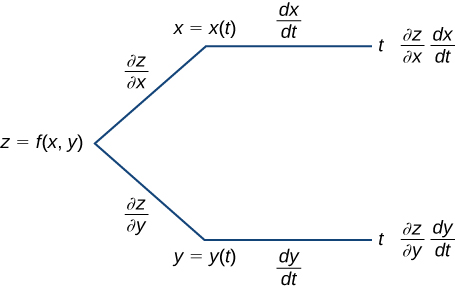
It is often useful to create a visual representation of [link] for the chain rule. This is called a tree diagram for the chain rule for functions of one variable and it provides a way to remember the formula ([link]). This diagram can be expanded for functions of more than one variable, as we shall see very shortly.

In this diagram, the leftmost corner corresponds to
Since
has two independent variables, there are two lines coming from this corner. The upper branch corresponds to the variable
and the lower branch corresponds to the variable
Since each of these variables is then dependent on one variable
one branch then comes from
and one branch comes from
Last, each of the branches on the far right has a label that represents the path traveled to reach that branch. The top branch is reached by following the
branch, then the
branch; therefore, it is labeled
The bottom branch is similar: first the
branch, then the
branch. This branch is labeled
To get the formula for
add all the terms that appear on the rightmost side of the diagram. This gives us [link].
In [link],
is a function of
and both
and
are functions of the independent variables
Suppose
and
are differentiable functions of
and
and
is a differentiable function of
Then,
is a differentiable function of
and
and
We can draw a tree diagram for each of these formulas as well as follows.
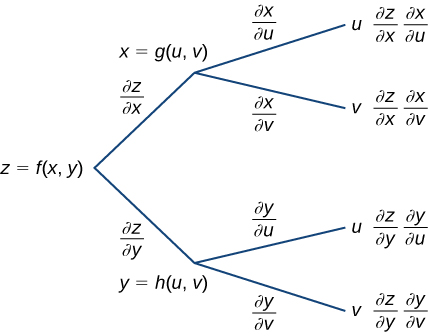
To derive the formula for
start from the left side of the diagram, then follow only the branches that end with
and add the terms that appear at the end of those branches. For the formula for
follow only the branches that end with
and add the terms that appear at the end of those branches.
There is an important difference between these two chain rule theorems. In [link], the left-hand side of the formula for the derivative is not a partial derivative, but in [link] it is. The reason is that, in [link],
is ultimately a function of
alone, whereas in [link],
is a function of both
Now that we’ve see how to extend the original chain rule to functions of two variables, it is natural to ask: Can we extend the rule to more than two variables? The answer is yes, as the generalized chain rule states.
Let
be a differentiable function of
independent variables, and for each
let
be a differentiable function of
independent variables. Then
for any
In the next example we calculate the derivative of a function of three independent variables in which each of the three variables is dependent on two other variables.
Calculate
and
using the following functions:
The formulas for
and
are
Therefore, there are nine different partial derivatives that need to be calculated and substituted. We need to calculate each of them:
Now, we substitute each of them into the first formula to calculate
then substitute
and
into this equation:
Next, we calculate
then we substitute
and
into this equation:
Calculate
and
given the following functions:
Calculate nine partial derivatives, then use the same formulas from [link].
Create a tree diagram for the case when
and write out the formulas for the three partial derivatives of
Starting from the left, the function
has three independent variables:
Therefore, three branches must be emanating from the first node. Each of these three branches also has three branches, for each of the variables
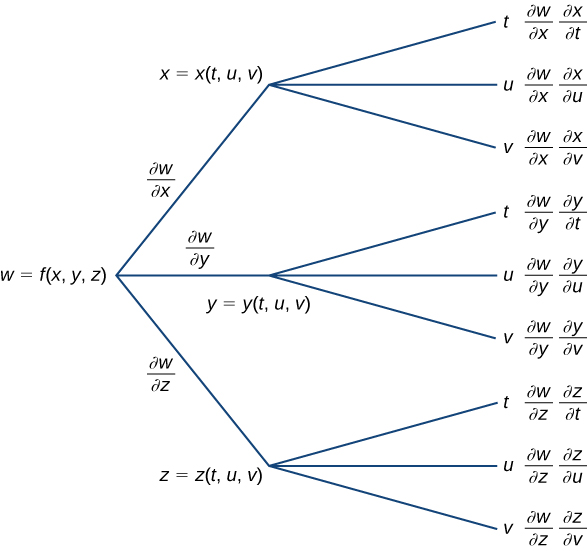
The three formulas are
Create a tree diagram for the case when
and write out the formulas for the three partial derivatives of
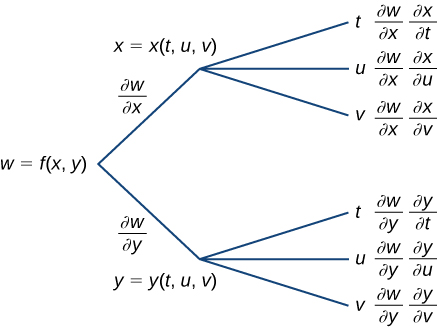
Determine the number of branches that emanate from each node in the tree.
Recall from Implicit Differentiation that implicit differentiation provides a method for finding
when
is defined implicitly as a function of
The method involves differentiating both sides of the equation defining the function with respect to
then solving for
Partial derivatives provide an alternative to this method.
Consider the ellipse defined by the equation
as follows.
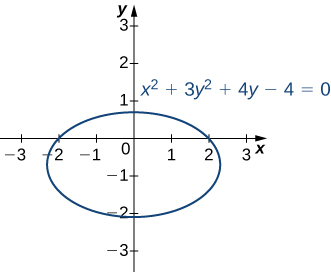
This equation implicitly defines
as a function of
As such, we can find the derivative
using the method of implicit differentiation:
We can also define a function
by using the left-hand side of the equation defining the ellipse. Then
The ellipse
can then be described by the equation
Using this function and the following theorem gives us an alternative approach to calculating
Suppose the function
defines
implicitly as a function
of
via the equation
Then
provided
If the equation
defines
implicitly as a differentiable function of
then
as long as
[link] is a direct consequence of [link]. In particular, if we assume that
is defined implicitly as a function of
via the equation
we can apply the chain rule to find
Solving this equation for
gives [link]. [link] can be derived in a similar fashion.
Let’s now return to the problem that we started before the previous theorem. Using [link] and the function
we obtain
Then [link] gives
which is the same result obtained by the earlier use of implicit differentiation.
if
is defined implicitly as a function of
via the equation
What is the equation of the tangent line to the graph of this curve at point
and
given
Find
if
is defined implicitly as a function of
by the equation
What is the equation of the tangent line to the graph of this curve at point
Equation of the tangent line:
For the following exercises, use the information provided to solve the problem.
Let
where
and
Find
Let
where
and
Find
and
If
and
find
and
If
and
find
If
and
find
and express the answer in terms of
and
Suppose
and
where
and
Find
For the following exercises, find
using the chain rule and direct substitution.
Let
and
Express
as a function of
and find
directly. Then, find
using the chain rule.
in both cases
Let
where
and
Find
Let
where
and
Find
when
and
For the following exercises, find
using partial derivatives.
Find
using the chain rule where
and
Let
and
Find
Let
and
Find
Find
by the chain rule where
and
Let
and
Find
and
and
Let
where
and
Find
and
If
and
find
and
when
and
Find
if
and
If
and
find
For the following exercises, use this information: A function
is said to be homogeneous of degree
if
For all homogeneous functions of degree
the following equation is true:
Show that the given function is homogeneous and verify that
The volume of a right circular cylinder is given by
where
is the radius of the cylinder and y is the cylinder height. Suppose
and
are functions of
given by
and
so that
are both increasing with time. How fast is the volume increasing when
and
The pressure
of a gas is related to the volume and temperature by the formula
where temperature is expressed in kelvins. Express the pressure of the gas as a function of both
and
Find
when
cm3/min,
K/min,
cm3, and
The radius of a right circular cone is increasing at
cm/min whereas the height of the cone is decreasing at
cm/min. Find the rate of change of the volume of the cone when the radius is
cm and the height is
cm.
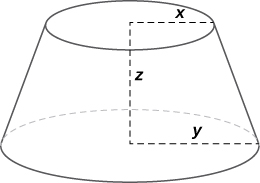
The volume of a frustum of a cone is given by the formula
where
is the radius of the smaller circle,
is the radius of the larger circle, and
is the height of the frustum (see figure). Find the rate of change of the volume of this frustum when
A closed box is in the shape of a rectangular solid with dimensions
(Dimensions are in inches.) Suppose each dimension is changing at the rate of
in./min. Find the rate of change of the total surface area of the box when
The total resistance in a circuit that has three individual resistances represented by
and
is given by the formula
Suppose at a given time the
resistance is
the y resistance is
and the
resistance is
Also, suppose the
resistance is changing at a rate of
the
resistance is changing at the rate of
and the
resistance has no change. Find the rate of change of the total resistance in this circuit at this time.
The temperature
at a point
is
and is measured using the Celsius scale. A fly crawls so that its position after
seconds is given by
and
where
are measured in centimeters. The temperature function satisfies
and
How fast is the temperature increasing on the fly’s path after
sec?
The
components of a fluid moving in two dimensions are given by the following functions:
and
The speed of the fluid at the point
is
Find
and
using the chain rule.
Let
where
Use a tree diagram and the chain rule to find an expression for
the intermediate variables are the variables that are independent in the outer function but dependent on other variables as well; in the function
the variables
are examples of intermediate variables

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: