In this section, we consider the problem of finding the tangent plane to a surface, which is analogous to finding the equation of a tangent line to a curve when the curve is defined by the graph of a function of one variable,
The slope of the tangent line at the point
is given by
what is the slope of a tangent plane? We learned about the equation of a plane in Equations of Lines and Planes in Space; in this section, we see how it can be applied to the problem at hand.
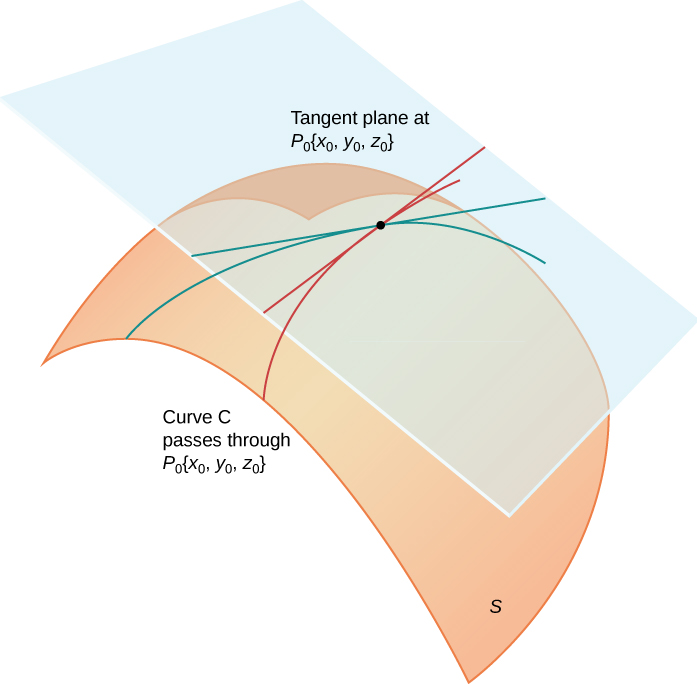
Intuitively, it seems clear that, in a plane, only one line can be tangent to a curve at a point. However, in three-dimensional space, many lines can be tangent to a given point. If these lines lie in the same plane, they determine the tangent plane at that point. A tangent plane at a regular point contains all of the lines tangent to that point. A more intuitive way to think of a tangent plane is to assume the surface is smooth at that point (no corners). Then, a tangent line to the surface at that point in any direction does not have any abrupt changes in slope because the direction changes smoothly.
Let
be a point on a surface
and let
be any curve passing through
and lying entirely in
If the tangent lines to all such curves
at
lie in the same plane, then this plane is called the tangent plane to
at
([link]).

For a tangent plane to a surface to exist at a point on that surface, it is sufficient for the function that defines the surface to be differentiable at that point. We define the term tangent plane here and then explore the idea intuitively.
Let
be a surface defined by a differentiable function
and let
be a point in the domain of
Then, the equation of the tangent plane to
at
is given by
To see why this formula is correct, let’s first find two tangent lines to the surface
The equation of the tangent line to the curve that is represented by the intersection of
with the vertical trace given by
is
Similarly, the equation of the tangent line to the curve that is represented by the intersection of
with the vertical trace given by
is
A parallel vector to the first tangent line is
a parallel vector to the second tangent line is
We can take the cross product of these two vectors:
This vector is perpendicular to both lines and is therefore perpendicular to the tangent plane. We can use this vector as a normal vector to the tangent plane, along with the point
in the equation for a plane:
Solving this equation for
gives [link].
Find the equation of the tangent plane to the surface defined by the function
at point
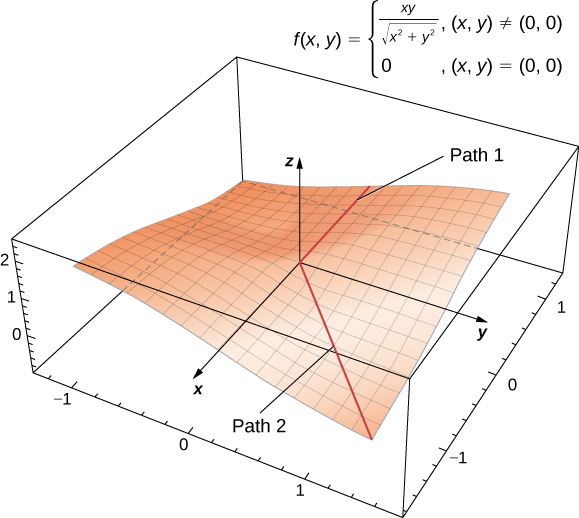
A tangent plane to a surface does not always exist at every point on the surface. Consider the function
The graph of this function follows.
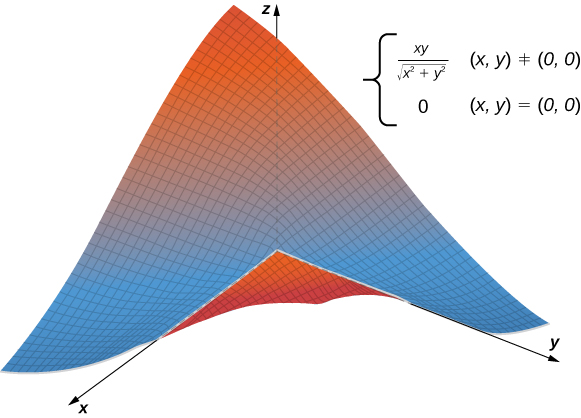
If either
or
then
so the value of the function does not change on either the x- or y-axis. Therefore,
so as either
approach zero, these partial derivatives stay equal to zero. Substituting them into [link] gives
as the equation of the tangent line. However, if we approach the origin from a different direction, we get a different story. For example, suppose we approach the origin along the line
If we put
into the original function, it becomes
When
the slope of this curve is equal to
when
the slope of this curve is equal to
This presents a problem. In the definition of tangent plane, we presumed that all tangent lines through point
(in this case, the origin) lay in the same plane. This is clearly not the case here. When we study differentiable functions, we will see that this function is not differentiable at the origin.
Recall from Linear Approximations and Differentials that the formula for the linear approximation of a function
at the point
is given by
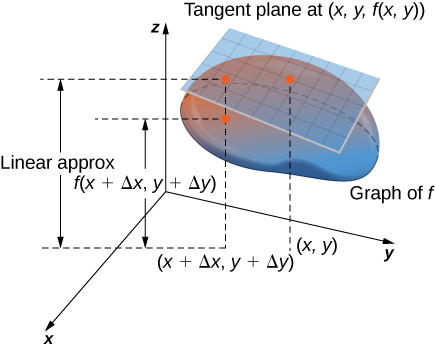
The diagram for the linear approximation of a function of one variable appears in the following graph.
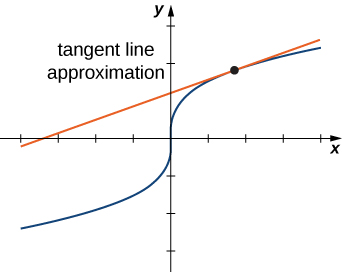
The tangent line can be used as an approximation to the function
for values of
reasonably close to
When working with a function of two variables, the tangent line is replaced by a tangent plane, but the approximation idea is much the same.
Given a function
with continuous partial derivatives that exist at the point
the linear approximation of
at the point
is given by the equation
Notice that this equation also represents the tangent plane to the surface defined by
at the point
The idea behind using a linear approximation is that, if there is a point
at which the precise value of
is known, then for values of
reasonably close to
the linear approximation (i.e., tangent plane) yields a value that is also reasonably close to the exact value of
([link]). Furthermore the plane that is used to find the linear approximation is also the tangent plane to the surface at the point
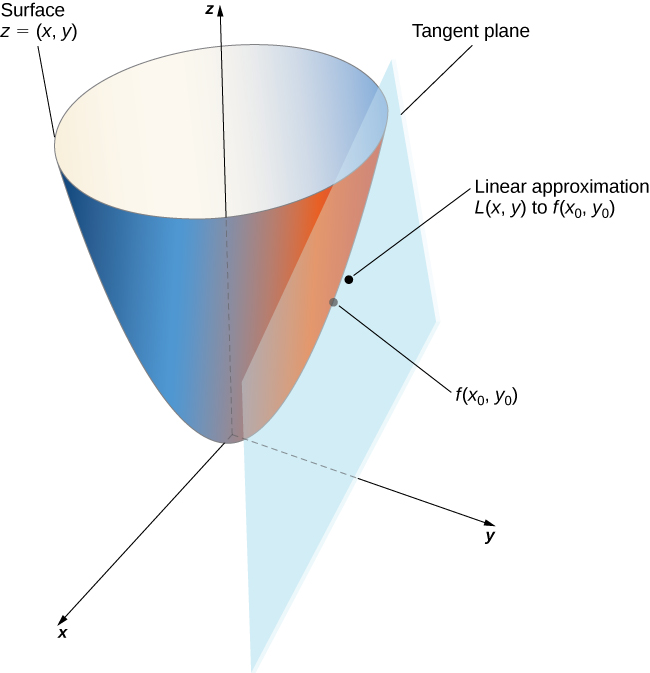
Given the function
approximate
using point
for
What is the approximate value of
to four decimal places?
Given the function
approximate
using point
for
What is the approximate value of
to four decimal places?
so
When working with a function
of one variable, the function is said to be differentiable at a point
if
exists. Furthermore, if a function of one variable is differentiable at a point, the graph is “smooth” at that point (i.e., no corners exist) and a tangent line is well-defined at that point.
The idea behind differentiability of a function of two variables is connected to the idea of smoothness at that point. In this case, a surface is considered to be smooth at point
if a tangent plane to the surface exists at that point. If a function is differentiable at a point, then a tangent plane to the surface exists at that point. Recall the formula for a tangent plane at a point
is given by
For a tangent plane to exist at the point
the partial derivatives must therefore exist at that point. However, this is not a sufficient condition for smoothness, as was illustrated in [link]. In that case, the partial derivatives existed at the origin, but the function also had a corner on the graph at the origin.
A function
is differentiable at a point
if, for all points
in a
disk around
we can write
where the error term
satisfies
The last term in [link] is referred to as the error term and it represents how closely the tangent plane comes to the surface in a small neighborhood
disk) of point
For the function
to be differentiable at
the function must be smooth—that is, the graph of
must be close to the tangent plane for points near
Show that the function
is differentiable at point
The function
is not differentiable at the origin. We can see this by calculating the partial derivatives. This function appeared earlier in the section, where we showed that
Substituting this information into [link] using
and
we get
Calculating
gives
Depending on the path taken toward the origin, this limit takes different values. Therefore, the limit does not exist and the function
is not differentiable at the origin as shown in the following figure.
Differentiability and continuity for functions of two or more variables are connected, the same as for functions of one variable. In fact, with some adjustments of notation, the basic theorem is the same.
Let
be a function of two variables with
in the domain of
If
is differentiable at
then
is continuous at
[link] shows that if a function is differentiable at a point, then it is continuous there. However, if a function is continuous at a point, then it is not necessarily differentiable at that point. For example,
is continuous at the origin, but it is not differentiable at the origin. This observation is also similar to the situation in single-variable calculus.
[link] further explores the connection between continuity and differentiability at a point. This theorem says that if the function and its partial derivatives are continuous at a point, the function is differentiable.
Let
be a function of two variables with
in the domain of
If
and
all exist in a neighborhood of
and are continuous at
then
is differentiable there.
Recall that earlier we showed that the function
was not differentiable at the origin. Let’s calculate the partial derivatives
and
The contrapositive of the preceding theorem states that if a function is not differentiable, then at least one of the hypotheses must be false. Let’s explore the condition that
must be continuous. For this to be true, it must be true that
Let
Then
If
then this expression equals
if
then it equals
In either case, the value depends on
so the limit fails to exist.
In Linear Approximations and Differentials we first studied the concept of differentials. The differential of
written
is defined as
The differential is used to approximate
where
Extending this idea to the linear approximation of a function of two variables at the point
yields the formula for the total differential for a function of two variables.
Let
be a function of two variables with
in the domain of
and let
and
be chosen so that
is also in the domain of
If
is differentiable at the point
then the differentials
and
are defined as
The differential
also called the total differential of
at
is defined as
Notice that the symbol
is not used to denote the total differential; rather,
appears in front of
Now, let’s define
We use
to approximate
so
Therefore, the differential is used to approximate the change in the function
at the point
for given values of
and
Since
this can be used further to approximate
See the following figure.
One such application of this idea is to determine error propagation. For example, if we are manufacturing a gadget and are off by a certain amount in measuring a given quantity, the differential can be used to estimate the error in the total volume of the gadget.
Find the differential
of the function
and use it to approximate
at point
Use
and
What is the exact value of
First, we must calculate
using
and
Then, we substitute these quantities into [link]:
This is the approximation to
The exact value of
is given by
Find the differential
of the function
and use it to approximate
at point
Use
and
What is the exact value of
All of the preceding results for differentiability of functions of two variables can be generalized to functions of three variables. First, the definition:
A function
is differentiable at a point
if for all points
in a
disk around
we can write
where the error term E satisfies
If a function of three variables is differentiable at a point
then it is continuous there. Furthermore, continuity of first partial derivatives at that point guarantees differentiability.
at the point
for given values of
and
where the error term
satisfies
where the error term
satisfies
For the following exercises, find a unit normal vector to the surface at the indicated point.
when
For the following exercises, as a useful review for techniques used in this section, find a normal vector and a tangent vector at point
Normal vector:
tangent vector:
Normal vector:
tangent vector:
For the following exercises, find the equation for the tangent plane to the surface at the indicated point. (Hint: Solve for
in terms of
and
For the following exercises, find parametric equations for the normal line to the surface at the indicated point. (Recall that to find the equation of a line in space, you need a point on the line,
and a vector
that is parallel to the line. Then the equation of the line is
at point
For the following exercises, use the figure shown here.
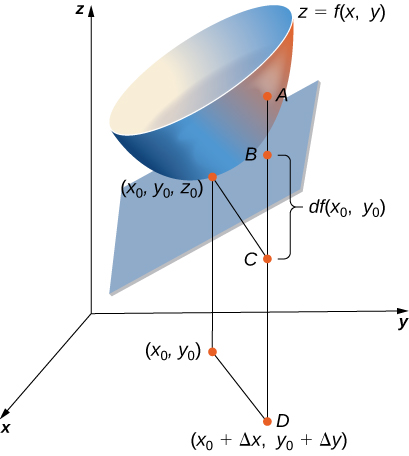
The length of line segment
is equal to what mathematical expression?
The length of line segment
is equal to what mathematical expression?
The differential of the function
Using the figure, explain what the length of line segment
represents.
For the following exercises, complete each task.
Show that
is differentiable at point
Using the definition of differentiability, we have
Find the total differential of the function
Show that
is differentiable at every point. In other words, show that
where both
and
approach zero as
approaches
for small
and
satisfies the definition of differentiability.
Find the total differential of the function
where
changes from
and
changes from
Let
Compute
from
to
and then find the approximate change in
from point
to point
Recall
and
and
are approximately equal.
and
They are relatively close.
The volume of a right circular cylinder is given by
Find the differential
Interpret the formula geometrically.
See the preceding problem. Use differentials to estimate the amount of aluminum in an enclosed aluminum can with diameter
and height
if the aluminum is
cm thick.
cm3
Use the differential
to approximate the change in
as
moves from point
to point
Compare this approximation with the actual change in the function.
Let
Find the exact change in the function and the approximate change in the function as
changes from
and
changes from
exact change
approximate change is
The two values are close.
The centripetal acceleration of a particle moving in a circle is given by
where
is the velocity and
is the radius of the circle. Approximate the maximum percent error in measuring the acceleration resulting from errors of
in
and
in
(Recall that the percentage error is the ratio of the amount of error over the original amount. So, in this case, the percentage error in
is given by
The radius
and height
of a right circular cylinder are measured with possible errors of
respectively. Approximate the maximum possible percentage error in measuring the volume (Recall that the percentage error is the ratio of the amount of error over the original amount. So, in this case, the percentage error in
is given by
The base radius and height of a right circular cone are measured as
in. and
in., respectively, with a possible error in measurement of as much as
in. each. Use differentials to estimate the maximum error in the calculated volume of the cone.
The electrical resistance
produced by wiring resistors
and
in parallel can be calculated from the formula
If
and
are measured to be
and
respectively, and if these measurements are accurate to within
estimate the maximum possible error in computing
(The symbol
represents an ohm, the unit of electrical resistance.)
The area of an ellipse with axes of length
and
is given by the formula
Approximate the percent change in the area when
increases by
and
increases by
The period
of a simple pendulum with small oscillations is calculated from the formula
where
is the length of the pendulum and
is the acceleration resulting from gravity. Suppose that
and
have errors of, at most,
and
respectively. Use differentials to approximate the maximum percentage error in the calculated value of
Electrical power
is given by
where
is the voltage and
is the resistance. Approximate the maximum percentage error in calculating power if
is applied to a
resistor and the possible percent errors in measuring
and
are
and
respectively.
For the following exercises, find the linear approximation of each function at the indicated point.
[T] Find the equation of the tangent plane to the surface
at point
and graph the surface and the tangent plane at the point.
[T] Find the equation for the tangent plane to the surface at the indicated point, and graph the surface and the tangent plane:
[T] Find the equation of the tangent plane to the surface
at point
and graph the surface and the tangent plane.
is differentiable at
if
can be expressed in the form
where the error term
satisfies
and a tangent plane to the function at a point
we can approximate
for points near
using the tangent plane formula
that is differentiable at a point
the equation of the tangent plane to the surface
is given by
at
is given by the formula

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: