In this section, we study formulas related to curves in both two and three dimensions, and see how they are related to various properties of the same curve. For example, suppose a vector-valued function describes the motion of a particle in space. We would like to determine how far the particle has traveled over a given time interval, which can be described by the arc length of the path it follows. Or, suppose that the vector-valued function describes a road we are building and we want to determine how sharply the road curves at a given point. This is described by the curvature of the function at that point. We explore each of these concepts in this section.
We have seen how a vector-valued function describes a curve in either two or three dimensions. Recall [link], which states that the formula for the arc length of a curve defined by the parametric functions
is given by
In a similar fashion, if we define a smooth curve using a vector-valued function
where
the arc length is given by the formula
In three dimensions, if the vector-valued function is described by
over the same interval
the arc length is given by
where t lies within the interval
the arc length of C over the interval is
where t lies within the interval
the arc length of C over the interval is
The two formulas are very similar; they differ only in the fact that a space curve has three component functions instead of two. Note that the formulas are defined for smooth curves: curves where the vector-valued function
is differentiable with a non-zero derivative. The smoothness condition guarantees that the curve has no cusps (or corners) that could make the formula problematic.
We now return to the helix introduced earlier in this chapter. A vector-valued function that describes a helix can be written in the form
where R represents the radius of the helix, h represents the height (distance between two consecutive turns), and the helix completes N turns. Let’s derive a formula for the arc length of this helix using [link]. First of all,
Therefore,
This gives a formula for the length of a wire needed to form a helix with N turns that has radius R and height h.
We now have a formula for the arc length of a curve defined by a vector-valued function. Let’s take this one step further and examine what an arc-length function is.
If a vector-valued function represents the position of a particle in space as a function of time, then the arc-length function measures how far that particle travels as a function of time. The formula for the arc-length function follows directly from the formula for arc length:
If the curve is in two dimensions, then only two terms appear under the square root inside the integral. The reason for using the independent variable u is to distinguish between time and the variable of integration. Since
measures distance traveled as a function of time,
measures the speed of the particle at any given time. Since we have a formula for
in [link], we can differentiate both sides of the equation:
If we assume that
defines a smooth curve, then the arc length is always increasing, so
for
Last, if
is a curve on which
for all t, then
which means that t represents the arc length as long as
Let
describe a smooth curve for
Then the arc-length function is given by
Furthermore,
If
for all
then the parameter t represents the arc length from the starting point at
A useful application of this theorem is to find an alternative parameterization of a given curve, called an arc-length parameterization. Recall that any vector-valued function can be reparameterized via a change of variables. For example, if we have a function
that parameterizes a circle of radius 3, we can change the parameter from t to
obtaining a new parameterization
The new parameterization still defines a circle of radius 3, but now we need only use the values
to traverse the circle once.
Suppose that we find the arc-length function
and are able to solve this function for t as a function of s. We can then reparameterize the original function
by substituting the expression for t back into
The vector-valued function is now written in terms of the parameter s. Since the variable s represents the arc length, we call this an arc-length parameterization of the original function
One advantage of finding the arc-length parameterization is that the distance traveled along the curve starting from
is now equal to the parameter s. The arc-length parameterization also appears in the context of curvature (which we examine later in this section) and line integrals, which we study in the Introduction to Vector Calculus.
Find the arc-length parameterization for each of the following curves:
which gives the relationship between the arc length s and the parameter t as
so,
Next we replace the variable t in the original function
with the expression
to obtain
This is the arc-length parameterization of
Since the original restriction on t was given by
the restriction on s becomes
or
Therefore, the relationship between the arc length s and the parameter t is
so
Substituting this into the original function
yields
This is an arc-length parameterization of
The original restriction on the parameter
was
so the restriction on s is
or
Find the arc-length function for the helix
Then, use the relationship between the arc length and the parameter t to find an arc-length parameterization of
or
Substituting this into
gives
Start by finding the arc-length function.
An important topic related to arc length is curvature. The concept of curvature provides a way to measure how sharply a smooth curve turns. A circle has constant curvature. The smaller the radius of the circle, the greater the curvature.
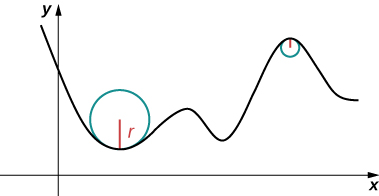
Think of driving down a road. Suppose the road lies on an arc of a large circle. In this case you would barely have to turn the wheel to stay on the road. Now suppose the radius is smaller. In this case you would need to turn more sharply to stay on the road. In the case of a curve other than a circle, it is often useful first to inscribe a circle to the curve at a given point so that it is tangent to the curve at that point and “hugs” the curve as closely as possible in a neighborhood of the point ([link]). The curvature of the graph at that point is then defined to be the same as the curvature of the inscribed circle.

Let C be a smooth curve in the plane or in space given by
where
is the arc-length parameter. The curvature
at s is
Visit this website for more information about the curvature of a space curve.
The formula in the definition of curvature is not very useful in terms of calculation. In particular, recall that
represents the unit tangent vector to a given vector-valued function
and the formula for
is
To use the formula for curvature, it is first necessary to express
in terms of the arc-length parameter s, then find the unit tangent vector
for the function
then take the derivative of
with respect to s. This is a tedious process. Fortunately, there are equivalent formulas for curvature.
If C is a smooth curve given by
then the curvature
of C at t is given by
If C is a three-dimensional curve, then the curvature can be given by the formula
If C is the graph of a function
and both
and
exist, then the curvature
at point
is given by
The first formula follows directly from the chain rule:
where s is the arc length along the curve C. Dividing both sides by
and taking the magnitude of both sides gives
Since
this gives the formula for the curvature
of a curve C in terms of any parameterization of C:
In the case of a three-dimensional curve, we start with the formulas
and
Therefore,
We can take the derivative of this function using the scalar product formula:
Using these last two equations we get
Since
this reduces to
Since
is parallel to
and
is orthogonal to
it follows that
and
are orthogonal. This means that
so
Now we solve this equation for
and use the fact that
Then, we divide both sides by
This gives
This proves [link]. To prove [link], we start with the assumption that curve C is defined by the function
Then, we can define
Using the previous formula for curvature:
Therefore,
□
Find the curvature for each of the following curves at the given point:
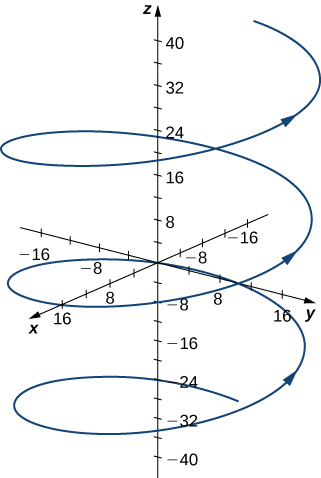
The curvature of the helix at
can be found by using [link]. First, calculate
Next, calculate
Last, apply [link]:
The curvature of this helix is constant at all points on the helix.
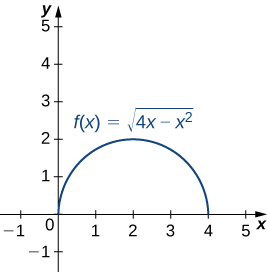
To find the curvature of this graph, we must use [link]. First, we calculate
and
Then, we apply [link]:
The curvature of this circle is equal to the reciprocal of its radius. There is a minor issue with the absolute value in [link]; however, a closer look at the calculation reveals that the denominator is positive for any value of x.
We have seen that the derivative
of a vector-valued function is a tangent vector to the curve defined by
and the unit tangent vector
can be calculated by dividing
by its magnitude. When studying motion in three dimensions, two other vectors are useful in describing the motion of a particle along a path in space: the principal unit normal vector and the binormal vector.
Let C be a three-dimensional smooth curve represented by r over an open interval I. If
then the principal unit normal vector at t is defined to be
The binormal vector at t is defined as
where
is the unit tangent vector.
Note that, by definition, the binormal vector is orthogonal to both the unit tangent vector and the normal vector. Furthermore,
is always a unit vector. This can be shown using the formula for the magnitude of a cross product
where
is the angle between
and
Since
is the derivative of a unit vector, property (vii) of the derivative of a vector-valued function tells us that
and
are orthogonal to each other, so
Furthermore, they are both unit vectors, so their magnitude is 1. Therefore,
and
is a unit vector.
The principal unit normal vector can be challenging to calculate because the unit tangent vector involves a quotient, and this quotient often has a square root in the denominator. In the three-dimensional case, finding the cross product of the unit tangent vector and the unit normal vector can be even more cumbersome. Fortunately, we have alternative formulas for finding these two vectors, and they are presented in Motion in Space.
For each of the following vector-valued functions, find the principal unit normal vector. Then, if possible, find the binormal vector.
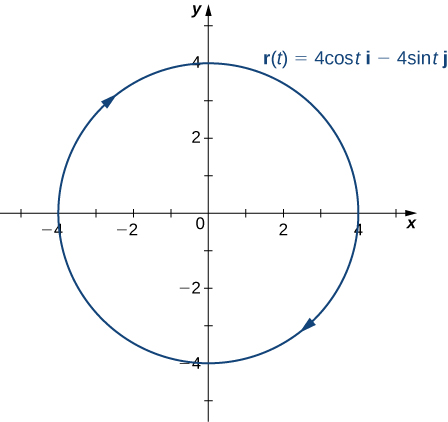
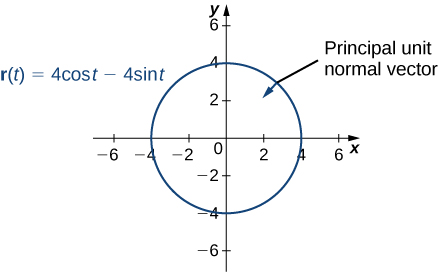
To find the principal unit normal vector, we first must find the unit tangent vector
Next, we use [link]:
Notice that the unit tangent vector and the principal unit normal vector are orthogonal to each other for all values of t:
Furthermore, the principal unit normal vector points toward the center of the circle from every point on the circle. Since
defines a curve in two dimensions, we cannot calculate the binormal vector.
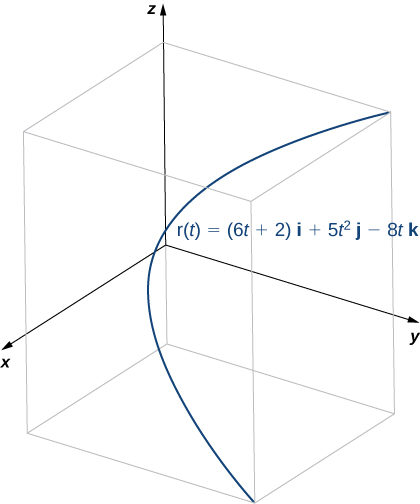
To find the principal unit normal vector, we first find the unit tangent vector
Next, we calculate
and
Therefore, according to [link]:
Once again, the unit tangent vector and the principal unit normal vector are orthogonal to each other for all values of t:
Last, since
represents a three-dimensional curve, we can calculate the binormal vector using [link]:
Find the unit normal vector for the vector-valued function
and evaluate it at
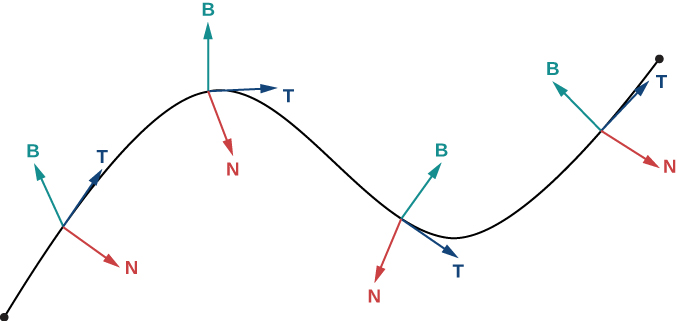
For any smooth curve in three dimensions that is defined by a vector-valued function, we now have formulas for the unit tangent vector T, the unit normal vector N, and the binormal vector B. The unit normal vector and the binormal vector form a plane that is perpendicular to the curve at any point on the curve, called the normal plane. In addition, these three vectors form a frame of reference in three-dimensional space called the Frenet frame of reference (also called the TNB frame) ([link]). Lat, the plane determined by the vectors T and N forms the osculating plane of C at any point P on the curve.
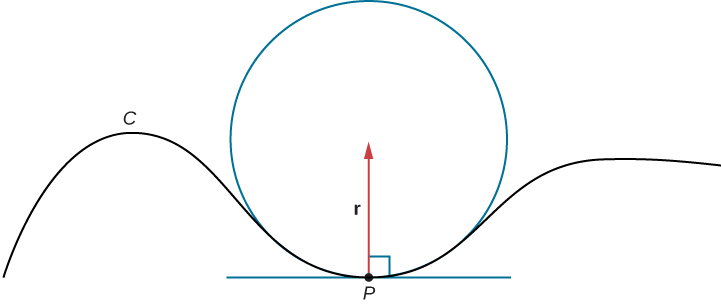
Suppose we form a circle in the osculating plane of C at point P on the curve. Assume that the circle has the same curvature as the curve does at point P and let the circle have radius r. Then, the curvature of the circle is given by
We call r the radius of curvature of the curve, and it is equal to the reciprocal of the curvature. If this circle lies on the concave side of the curve and is tangent to the curve at point P, then this circle is called the osculating circle of C at P, as shown in the following figure.
For more information on osculating circles, see this demonstration on curvature and torsion, this article on osculating circles, and this discussion of Serret formulas.
To find the equation of an osculating circle in two dimensions, we need find only the center and radius of the circle.
Find the equation of the osculating circle of the helix defined by the function
at
[link] shows the graph of
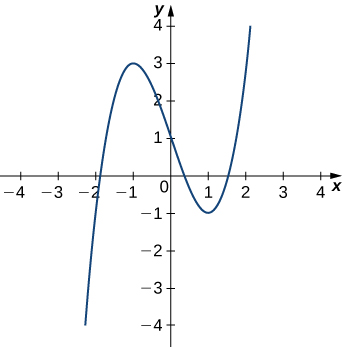
First, let’s calculate the curvature at
This gives
Therefore, the radius of the osculating circle is given by
Next, we then calculate the coordinates of the center of the circle. When
the slope of the tangent line is zero. Therefore, the center of the osculating circle is directly above the point on the graph with coordinates
The center is located at
The formula for a circle with radius r and center
is given by
Therefore, the equation of the osculating circle is
The graph and its osculating circle appears in the following graph.
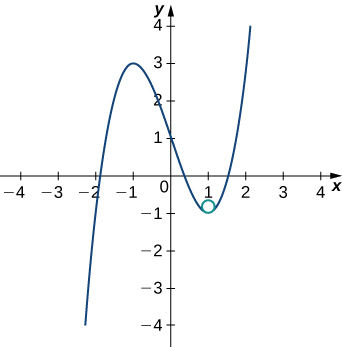
Find the equation of the osculating circle of the curve defined by the vector-valued function
at
At the point
the curvature is equal to 4. Therefore, the radius of the osculating circle is
A graph of this function appears next:* * *
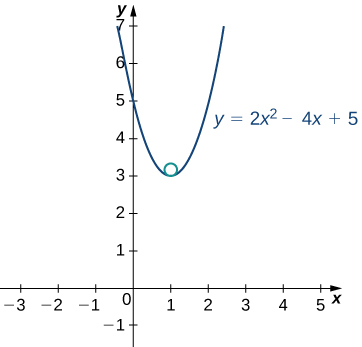 The vertex of this parabola is located at the point
The vertex of this parabola is located at the point
Furthermore, the center of the osculating circle is directly above the vertex. Therefore, the coordinates of the center are
The equation of the osculating circle is
Use [link] to find the curvature of the graph, then draw a graph of the function around
to help visualize the circle in relation to the graph.
This formula is valid in both two and three dimensions.
where
is the unit tangent vector.
Find the arc length of the curve on the given interval.
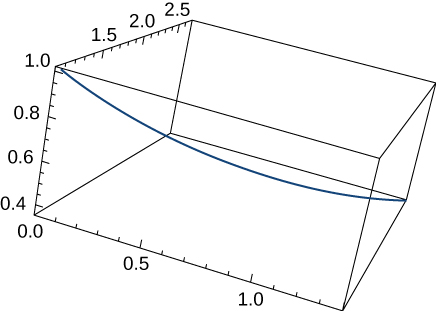
This portion of the graph is shown here:
This portion of the graph is shown here:
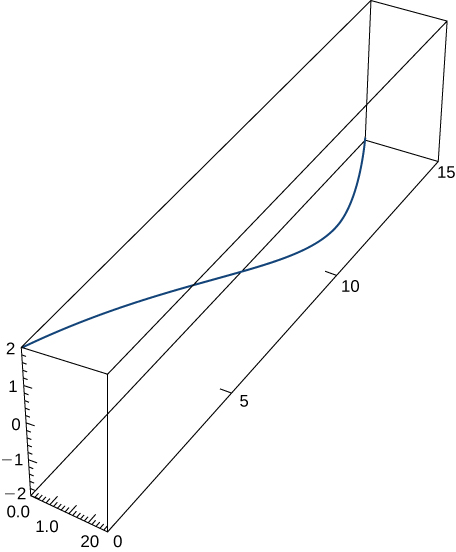
over the interval
Here is the portion of the graph on the indicated interval:
Find the length of one turn of the helix given by
Length
Find the arc length of the vector-valued function
over
A particle travels in a circle with the equation of motion
Find the distance traveled around the circle by the particle.
Set up an integral to find the circumference of the ellipse with the equation
Find the length of the curve
over the interval
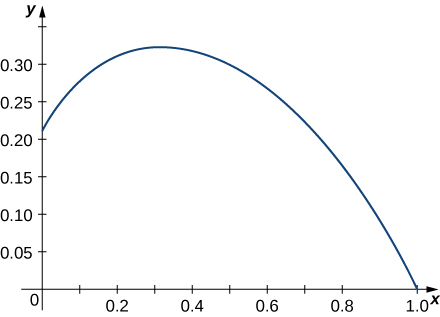
The graph is shown here:
Find the length of the curve
for
The position function for a particle is
Find the unit tangent vector and the unit normal vector at
Given
find the binormal vector
Given
determine the tangent vector
Given
determine the unit tangent vector
evaluated at
Given
find the unit normal vector
evaluated at
Given
find the unit normal vector evaluated at
Given
find the unit tangent vector
The graph is shown here:
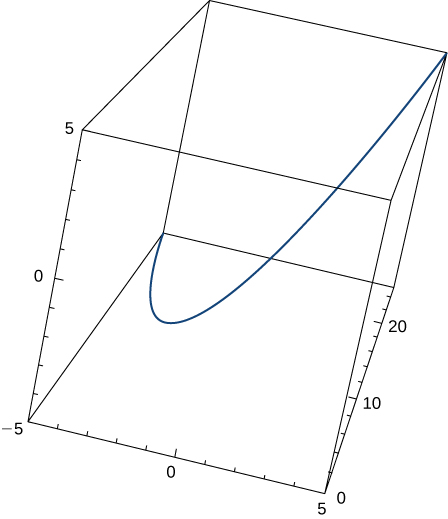
Find the unit tangent vector
and unit normal vector
at
for the plane curve
The graph is shown here:
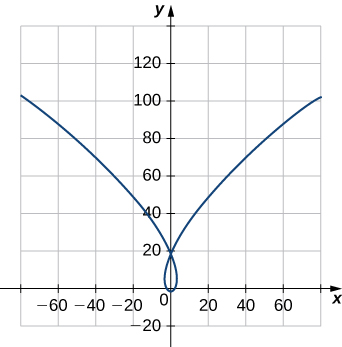
Find the unit tangent vector
for
Find the principal normal vector to the curve
at the point determined by
Find
for the curve
Find
for the curve
Find the unit normal vector
for
Find the unit tangent vector
for
Find the arc-length function
for the line segment given by
Write r as a parameter of s.
Arc-length function:
r as a parameter of s:
Parameterize the helix
using the arc-length parameter s, from
Parameterize the curve using the arc-length parameter s, at the point at which
for
Find the curvature of the curve
at
(Note: The graph is an ellipse.)
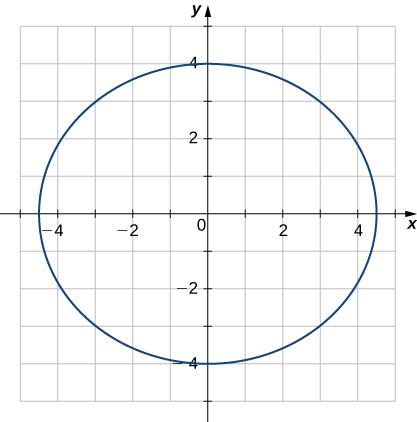
Find the x-coordinate at which the curvature of the curve
is a maximum value.
The maximum value of the curvature occurs at
Find the curvature of the curve
Does the curvature depend upon the parameter t?
Find the curvature
for the curve
at the point
Find the curvature
for the curve
at the point
Find the curvature
of the curve
The graph is shown here:
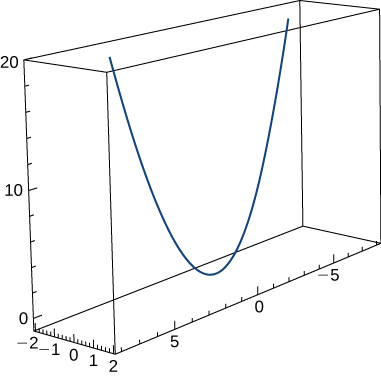
Find the curvature of
Find the curvature of
at point
At what point does the curve
have maximum curvature?
What happens to the curvature as
for the curve
The curvature approaches zero.
Find the point of maximum curvature on the curve
Find the equations of the normal plane and the osculating plane of the curve
at point
and
Find equations of the osculating circles of the ellipse
at the points
and
Find the equation for the osculating plane at point
on the curve
Find the radius of curvature of
at the point
Find the curvature at each point
on the hyperbola
Calculate the curvature of the circular helix
Find the radius of curvature of
at point
Find the radius of curvature of the hyperbola
at point
A particle moves along the plane curve C described by
Solve the following problems.
Find the length of the curve over the interval
Find the curvature of the plane curve at
Describe the curvature as t increases from
to
The curvature is decreasing over this interval.
The surface of a large cup is formed by revolving the graph of the function
from
to
about the y-axis (measured in centimeters).
[T] Use technology to graph the surface.
Find the curvature
of the generating curve as a function of x.
[T] Use technology to graph the curvature function.
that describes the arc length of curve C as a function of t
is differentiable with a non-zero derivative

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: