Calculus of Vector-Valued Functions

To study the calculus of vector-valued functions, we follow a similar path to the one we took in studying real-valued functions. First, we define the derivative, then we examine applications of the derivative, then we move on to defining integrals. However, we will find some interesting new ideas along the way as a result of the vector nature of these functions and the properties of space curves.

Derivatives of Vector-Valued Functions

Now that we have seen what a vector-valued function is and how to take its limit, the next step is to learn how to differentiate a vector-valued function. The definition of the derivative of a vector-valued function is nearly identical to the definition of a real-valued function of one variable. However, because the range of a vector-valued function consists of vectors, the same is true for the range of the derivative of a vector-valued function.

Many of the rules for calculating derivatives of real-valued functions can be applied to calculating the derivatives of vector-valued functions as well. Recall that the derivative of a real-valued function can be interpreted as the slope of a tangent line or the instantaneous rate of change of the function. The derivative of a vector-valued function can be understood to be an instantaneous rate of change as well; for example, when the function represents the position of an object at a given point in time, the derivative represents its velocity at that same point in time.

Notice that in the calculations in [link], we could also obtain the answer by first calculating the derivative of each component function, then putting these derivatives back into the vector-valued function. This is always true for calculating the derivative of a vector-valued function, whether it is in two or three dimensions. We state this in the following theorem. The proof of this theorem follows directly from the definitions of the limit of a vector-valued function and the derivative of a vector-valued function.

We can extend to vector-valued functions the properties of the derivative that we presented in the Introduction to Derivatives. In particular, the constant multiple rule, the sum and difference rules, the product rule, and the chain rule all extend to vector-valued functions. However, in the case of the product rule, there are actually three extensions: (1) for a real-valued function multiplied by a vector-valued function, (2) for the dot product of two vector-valued functions, and (3) for the cross product of two vector-valued functions.

Proof

The proofs of the first two properties follow directly from the definition of the derivative of a vector-valued function. The third property can be derived from the first two properties, along with the product rule from the Introduction to Derivatives. Let

u (t) = g (t) i + h (t) j .

The proof of property v. is similar to that of property iv. Property vi. can be proved using the chain rule. Last, property vii. follows from property iv:

Tangent Vectors and Unit Tangent Vectors

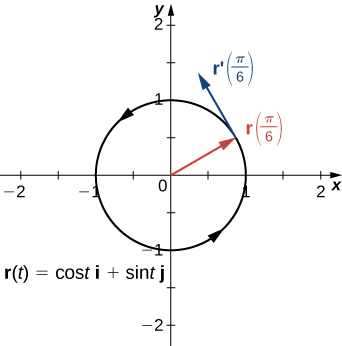
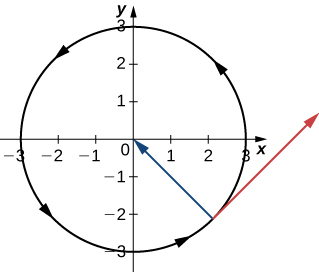
Recall from the Introduction to Derivatives that the derivative at a point can be interpreted as the slope of the tangent line to the graph at that point. In the case of a vector-valued function, the derivative provides a tangent vector to the curve represented by the function. Consider the vector-valued function

r (t) = cos t i + sin t j .

The graph of this function appears in [link], along with the vectors

r (\frac{π}{6})

This is an example of a tangent vector to the plane curve defined by

r (t) = cos t i + sin t j .

The unit tangent vector is exactly what it sounds like: a unit vector that is tangent to the curve. To calculate a unit tangent vector, first find the derivative

r^{'} (t) .

Second, calculate the magnitude of the derivative. The third step is to divide the derivative by its magnitude.

Integrals of Vector-Valued Functions

We introduced antiderivatives of real-valued functions in Antiderivatives and definite integrals of real-valued functions in The Definite Integral. Each of these concepts can be extended to vector-valued functions. Also, just as we can calculate the derivative of a vector-valued function by differentiating the component functions separately, we can calculate the antiderivative in the same manner. Furthermore, the Fundamental Theorem of Calculus applies to vector-valued functions as well.

The antiderivative of a vector-valued function appears in applications. For example, if a vector-valued function represents the velocity of an object at time t, then its antiderivative represents position. Or, if the function represents the acceleration of the object at a given time, then the antiderivative represents its velocity.

Since the indefinite integral of a vector-valued function involves indefinite integrals of the component functions, each of these component integrals contains an integration constant. They can all be different. For example, in the two-dimensional case, we can have

Key Concepts

Key Equations

Compute the derivatives of the vector-valued functions.

r (t) = t^{3} i + 3 t^{2} j + \frac{t^{3}}{6} k

〈 3 t^{2}, 6 t, \frac{1}{2} t^{2} 〉

r (t) = sin (t) i + cos (t) j + e^{t} k

r (t) = e^{− t} i + sin (3 t) ​ j + 10 \sqrt{t} k .

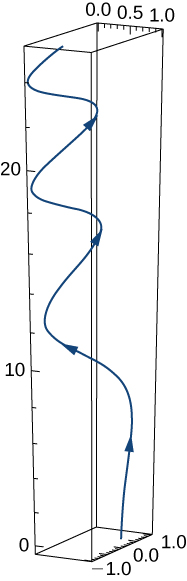
A sketch of the graph is shown here. Notice the varying periodic nature of the graph.

This figure is a 3 dimensional graph. It is a curve inside of a box. The curve starts at the bottom of the box and spirals around the middle, with upward orientation.

〈 − e^{− t}, 3 cos (3 t), \frac{5}{\sqrt{t}} 〉

r (t) = e^{t} i + 2 e^{t} j + k

r (t) = i + j + k

〈 0, 0, 0 〉

r (t) = t e^{t} i + t ln (t) j + sin (3 t) k

r (t) = \frac{1}{t + 1} i + arctan (t) j + ln t^{3} k

〈 \frac{−1}{{(t + 1)}^{2}}, \frac{1}{1 + t^{2}}, \frac{3}{t} 〉

r (t) = tan (2 t) i + sec (2 t) j + {sin}^{2} (t) k

r (t) = 3 i + 4 sin (3 t) j + t cos (t) k

〈 0, 12 cos (3 t), cos t - t sin t 〉

r (t) = t^{2} i + t e^{−2 t} j - 5 e^{−4 t} k

For the following problems, find a tangent vector at the indicated value of t.

r (t) = t i + sin (2 t) j + cos (3 t) k; t = \frac{π}{3}

\frac{1}{\sqrt{2}} 〈 1, −1, 0 〉

r (t) = 3 t^{3} i + 2 t^{2} j + \frac{1}{t} k; t = 1

r (t) = 3 e^{t} i + 2 e^{−3 t} j + 4 e^{2 t} k;

t = ln (2)

\frac{1}{\sqrt{1060.5625}} 〈 6, - \frac{3}{4}, 32 〉

r (t) = cos (2 t) i + 2 sin t j + t^{2} k; t = \frac{π}{2}

Find the unit tangent vector for the following parameterized curves.

r (t) = 6 i + cos (3 t) j + 3 sin (4 t) k,

0 \leq t < 2 π

\frac{1}{\sqrt{9 {sin}^{2} (3 t) + 144 {cos}^{2} (4 t)}} 〈 0, −3 sin (3 t), 12 cos (4 t) 〉

r (t) = cos t i + sin t j + sin t k,

0 \leq t < 2 π .

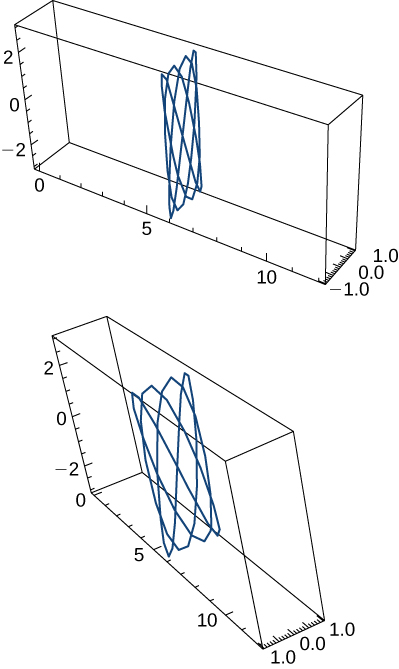
Two views of this curve are presented here:

This figure has two graphs. The first graph is inside a 3 dimensional box. It has a lattice-look to the graph in the middle of the box, crossing over itself. The second graph is the same as the first, with a different position of the box for a different perspective of the lattice-looking curve.

r (t) = 3 cos (4 t) i + 3 sin (4 t) j + 5 t k, 1 \leq t \leq 2

T (t) = \frac{−12}{13} sin (4 t) i + \frac{12}{13} cos (4 t) j + \frac{5}{13} k

r (t) = t i + 3 t j + t^{2} k

Let $r (t) = t i + t^{2} j - t^{4} k$

and $s (t) = sin (t) i + e^{t} j + cos (t) k .$

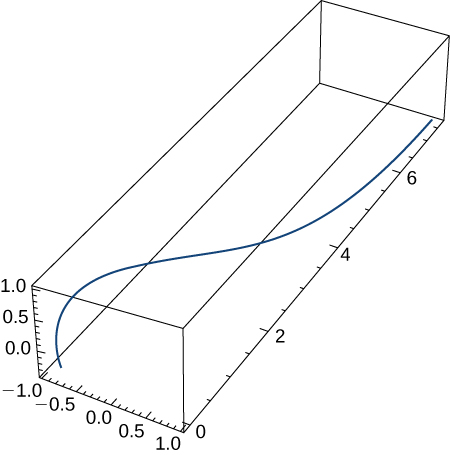
Here is the graph of the function:

This figure is a 3 dimensional graph. It is inside of a box. The box represents an octant. The curve in the graph starts at the lower left corner of the box and bends upward and out towards the other end of the box. Find the following.

\frac{d}{d t} [r (t^{2})]

〈 2 t, 4 t^{3}, −8 t^{7} 〉

\frac{d}{d t} [t^{2} \cdot s (t)]

\frac{d}{d t} [r (t) \cdot s (t)]

sin (t) + 2 t e^{t} - 4 t^{3} cos (t) + t cos (t) + t^{2} e^{t} + t^{4} sin (t)

Compute the first, second, and third derivatives of $r (t) = 3 t i + 6 ln (t) j + 5 e^{−3 t} k .$

Find $r' (t) \cdot r ″ (t) for r (t) = −3 t^{5} i + 5 t j + 2 t^{2} k .$

900 t^{7} + 16 t

The acceleration function, initial velocity, and initial position of a particle are* * *

a (t) = −5 cos t i - 5 sin t j, v (0) = 9 i + 2 j, and r (0) = 5 i .

Find $v (t) and r (t) .$

The position vector of a particle is $r (t) = 5 sec (2 t) i - 4 tan (t) j + 7 t^{2} k .$

Graph the position function and display a view of the graph that illustrates the asymptotic behavior of the function.
Find the velocity as t approaches but is not equal to $π / 4$
(if it exists).

Undefined or infinite

Find the velocity and the speed of a particle with the position function $r (t) = (\frac{2 t - 1}{2 t + 1}) i + ln (1 - 4 t^{2}) j .$

The speed of a particle is the magnitude of the velocity and is represented by $‖ r^{'} (t) ‖ .$

A particle moves on a circular path of radius b according to the function $r (t) = b cos (ω t) i + b sin (ω t) j,$

where $ω$

is the angular velocity, $d θ / d t .$

This figure is the graph of a circle centered at the origin with radius of 3. The orientation of the circle is counter-clockwise. Also, in the fourth quadrant there are two vectors. The first starts on the circle and terminates at the origin. The second vector is tangent at the same point in the fourth quadrant towards the x-axis.

Find the velocity function and show that $v (t)$

is always orthogonal to $r (t) .$

r' (t) = - b ω sin (ω t) i + b ω cos (ω t) j .

To show orthogonality, note that $r' (t) \cdot r (t) = 0 .$

Show that the speed of the particle is proportional to the angular velocity.

Evaluate $\frac{d}{d t} [u (t) \times u^{'} (t)]$

given $u (t) = t^{2} i - 2 t j + k .$

0 i + 2 j + 4 t j

Find the antiderivative of $r' (t) = cos (2 t) i - 2 sin t j + \frac{1}{1 + t^{2}} k$

that satisfies the initial condition $r (0) = 3 i - 2 j + k .$

Evaluate $\int_{0}^{3} ‖ t i + t^{2} j ‖ d t .$

\frac{1}{3} (10^{3 / 2} - 1)

An object starts from rest at point $P (1, 2, 0)$

and moves with an acceleration of $a (t) = j + 2 k,$

where $‖ a (t) ‖$

is measured in feet per second per second. Find the location of the object after $t = 2$

sec.

Show that if the speed of a particle traveling along a curve represented by a vector-valued function is constant, then the velocity function is always perpendicular to the acceleration function.

\begin{matrix} ‖ v (t) ‖ & = & k \\ v (t) \cdot v (t) & = & k \\ \frac{d}{d t} (v (t) \cdot v (t)) & = & \frac{d}{d t} k = 0 \\ v (t) \cdot v' (t) + v' (t) \cdot v (t) & = & 0 \\ 2 v (t) \cdot v' (t) & = & 0 \\ v (t) \cdot v' (t) & = & 0 . \end{matrix}

The last statement implies that the velocity and acceleration are perpendicular or orthogonal.* * *

Given $r (t) = t i + 3 t j + t^{2} k$

and $u (t) = 4 t i + t^{2} j + t^{3} k,$

find $\frac{d}{d t} (r (t) \times u (t)) .$

Given $r (t) = 〈 t + cos t, t - sin t 〉,$

find the velocity and the speed at any time.

v (t) = 〈 1 - sin t, 1 - cos t 〉,

speed = - v (t) ‖ = \sqrt{4 - 2 (sin t + cos t)}

Find the velocity vector for the function $r (t) = 〈 e^{t}, e^{− t}, 0 〉 .$

Find the equation of the tangent line to the curve $r (t) = 〈 e^{t}, e^{− t}, 0 〉$

at $t = 0 .$

x - 1 = t, y - 1 = - t, z - 0 = 0

Describe and sketch the curve represented by the vector-valued function $r (t) = 〈 6 t, 6 t - t^{2} 〉 .$

Locate the highest point on the curve $r (t) = 〈 6 t, 6 t - t^{2} 〉$

and give the value of the function at this point.

r (t) = 〈 18, 9 〉

at $t = 3$

The position vector for a particle is $r (t) = t i + t^{2} j + t^{3} k .$

The graph is shown here:

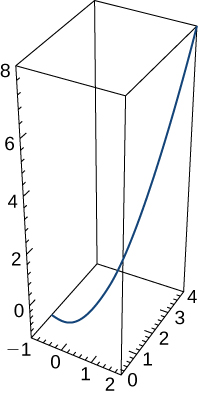
This figure is the graph of a curve in 3 dimensions. The curve is inside of a box. The box represents an octant. The curve begins at the bottom of the box to the left and curves upward to the top right corner.

Find the velocity vector at any time.

Find the speed of the particle at time $t = 2$

sec.

\sqrt{593}

Find the acceleration at time $t = 2$

sec.

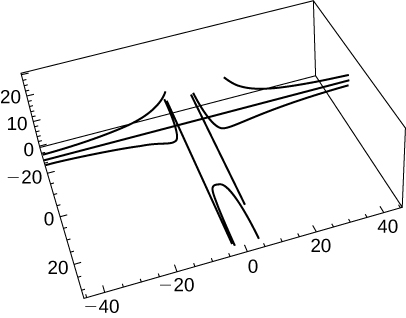
A particle travels along the path of a helix with the equation $r (t) = cos (t) i + sin (t) j + t k .$

See the graph presented here:

This figure is the graph of a curve in 3 dimensions. The curve is inside of a box. The box represents an octant. The curve is a helix and begins at the bottom of the box to the right and spirals upward. Find the following:

Velocity of the particle at any time

v (t) = 〈 − sin t, cos t, 1 〉

Speed of the particle at any time

Acceleration of the particle at any time

a (t) = - cos t i - sin t j + 0 j

Find the unit tangent vector for the helix.

A particle travels along the path of an ellipse with the equation $r (t) = cos t i + 2 sin t j + 0 k .$

Find the following:

Velocity of the particle

v (t) = 〈 − sin t, 2 cos t, 0 〉

Speed of the particle at $t = \frac{π}{4}$

Acceleration of the particle at $t = \frac{π}{4}$

a (t) = 〈 - \frac{\sqrt{2}}{2}, - \sqrt{2}, 0 〉

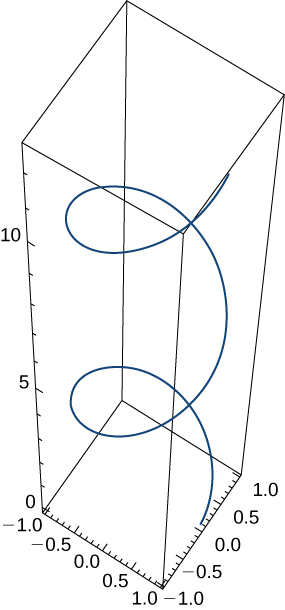
Given the vector-valued function $r (t) = 〈 tan t, sec t, 0 〉$

(graph is shown here), find the following:

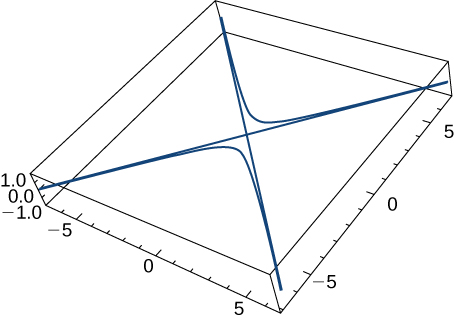
This figure is the graph of a curve in 3 dimensions. The curve is inside of a box. The box represents an octant. The curve has asymptotes that are the diagonals of the box. The curve is hyperbolic.

Velocity

Speed

‖ v (t) ‖ = \sqrt{{sec}^{4} t + {sec}^{2} t {tan}^{2} t} = \sqrt{{sec}^{2} t ({sec}^{2} t + {tan}^{2} t)}

Acceleration

Find the minimum speed of a particle traveling along the curve $r (t) = 〈 t + cos t, t - sin t 〉$

t \in [0, 2 π) .

Given $r (t) = t i + 2 sin t j + 2 cos t k$

and $u (t) = \frac{1}{t} i + 2 sin t j + 2 cos t k,$

find the following:

r (t) \times u (t)

\frac{d}{d t} (r (t) \times u (t))

〈 0, 2 sin t (t - \frac{1}{t}) - 2 cos t (1 + \frac{1}{t^{2}}), 2 sin t (1 + \frac{1}{t^{2}}) + 2 cos t (t - \frac{2}{t}) 〉

Now, use the product rule for the derivative of the cross product of two vectors and show this result is the same as the answer for the preceding problem.

Find the unit tangent vector T(t) for the following vector-valued functions.

r (t) = 〈 t, \frac{1}{t} 〉 .

The graph is shown here:

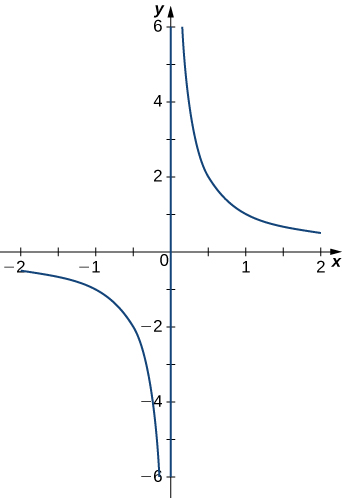
This figure is the graph of a hyperbolic curve. The y-axis is a vertical asymptote and the x-axis is the horizontal asymptote.

T (t) = 〈 \frac{t^{2}}{\sqrt{t^{4} + 1}}, \frac{−1}{\sqrt{t^{4} + 1}} 〉

r (t) = 〈 t cos t, t sin t 〉

r (t) = 〈 t + 1, 2 t + 1, 2 t + 2 〉

T (t) = \frac{1}{3} 〈 1, 2, 2 〉

Evaluate the following integrals:

\int (e^{t} i + sin t j + \frac{1}{2 t - 1} k) d t

\int_{0}^{1} r (t) d t,

where $r (t) = 〈 \sqrt[3]{t}, \frac{1}{t + 1}, e^{− t} 〉$

\frac{3}{4} i + ln (2) j + (1 - \frac{1}{e}) j

Calculus of Vector-Valued Functions

Derivatives of Vector-Valued Functions

Proof

Tangent Vectors and Unit Tangent Vectors

Integrals of Vector-Valued Functions

Key Concepts

Key Equations

Glossary