Imagine a mechanic turning a wrench to tighten a bolt. The mechanic applies a force at the end of the wrench. This creates rotation, or torque, which tightens the bolt. We can use vectors to represent the force applied by the mechanic, and the distance (radius) from the bolt to the end of the wrench. Then, we can represent torque by a vector oriented along the axis of rotation. Note that the torque vector is orthogonal to both the force vector and the radius vector.
In this section, we develop an operation called the cross product, which allows us to find a vector orthogonal to two given vectors. Calculating torque is an important application of cross products, and we examine torque in more detail later in the section.
The dot product is a multiplication of two vectors that results in a scalar. In this section, we introduce a product of two vectors that generates a third vector orthogonal to the first two. Consider how we might find such a vector. Let
and
be nonzero vectors. We want to find a vector
orthogonal to both
and
—that is, we want to find
such that
and
Therefore,
and
must satisfy
If we multiply the top equation by
and the bottom equation by
and subtract, we can eliminate the variable
which gives
If we select
we get a possible solution vector. Substituting these values back into the original equations gives
That is, vector
is orthogonal to both
and
which leads us to define the following operation, called the cross product.
Let
Then, the cross product
is vector
From the way we have developed
it should be clear that the cross product is orthogonal to both
and
However, it never hurts to check. To show that
is orthogonal to
we calculate the dot product of
and
In a similar manner, we can show that the cross product is also orthogonal to
Find
for
and
Express the answer using standard unit vectors.
Use the formula
Although it may not be obvious from [link], the direction of
is given by the right-hand rule. If we hold the right hand out with the fingers pointing in the direction of
then curl the fingers toward vector
the thumb points in the direction of the cross product, as shown.
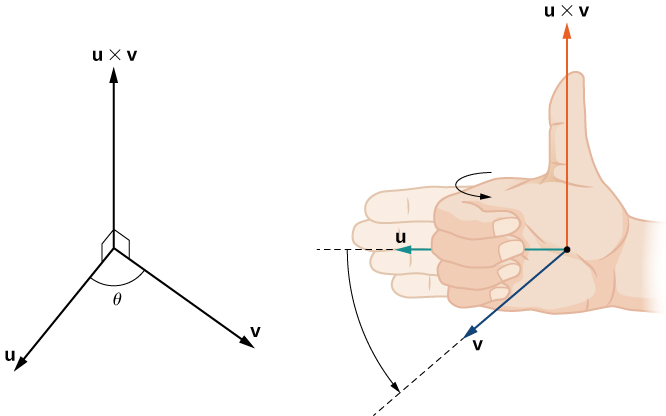
Notice what this means for the direction of
If we apply the right-hand rule to
we start with our fingers pointed in the direction of
then curl our fingers toward the vector
In this case, the thumb points in the opposite direction of
(Try it!)
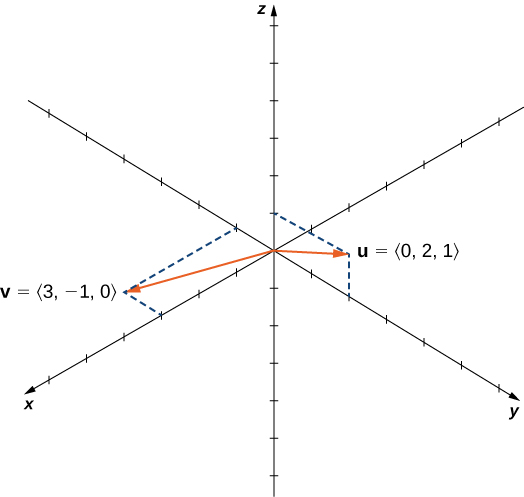
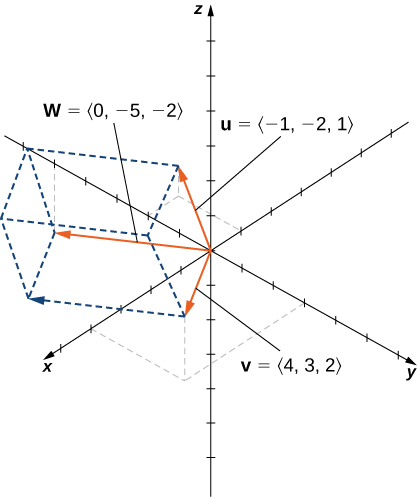
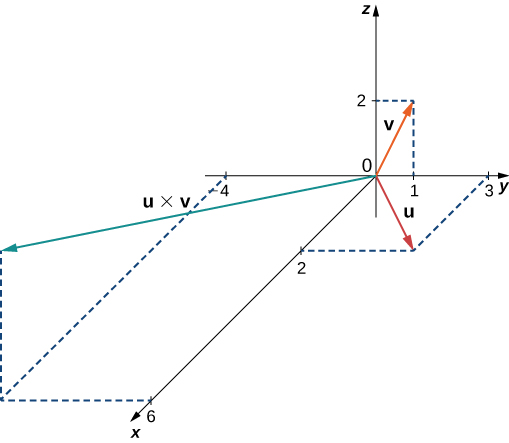
Let
and
Calculate
and
and graph them.
Suppose vectors
and
lie in the xy-plane (the z-component of each vector is zero). Now suppose the x- and y-components of
and the y-component of
are all positive, whereas the x-component of
is negative. Assuming the coordinate axes are oriented in the usual positions, in which direction does
point?
Up (the positive z-direction)
Remember the right-hand rule.
The cross products of the standard unit vectors
and
can be useful for simplifying some calculations, so let’s consider these cross products. A straightforward application of the definition shows that
(The cross product of two vectors is a vector, so each of these products results in the zero vector, not the scalar
It’s up to you to verify the calculations on your own.
Furthermore, because the cross product of two vectors is orthogonal to each of these vectors, we know that the cross product of
and
is parallel to
Similarly, the vector product of
and
is parallel to
and the vector product of
and
is parallel to
We can use the right-hand rule to determine the direction of each product. Then we have
These formulas come in handy later.
Find
We know that
Therefore,
Find
Remember the right-hand rule.
As we have seen, the dot product is often called the scalar product because it results in a scalar. The cross product results in a vector, so it is sometimes called the vector product. These operations are both versions of vector multiplication, but they have very different properties and applications. Let’s explore some properties of the cross product. We prove only a few of them. Proofs of the other properties are left as exercises.
Let
and
be vectors in space, and let
be a scalar.
For property
we want to show
We have
Unlike most operations we’ve seen, the cross product is not commutative. This makes sense if we think about the right-hand rule.
For property
this follows directly from the definition of the cross product. We have
Then, by property i.,
as well. Remember that the dot product of a vector and the zero vector is the scalar
whereas the cross product of a vector with the zero vector is the vector
Property
looks like the associative property, but note the change in operations:
□
Use the cross product properties to calculate
Use the properties of the cross product to calculate
So far in this section, we have been concerned with the direction of the vector
but we have not discussed its magnitude. It turns out there is a simple expression for the magnitude of
involving the magnitudes of
and
and the sine of the angle between them.
Let
and
be vectors, and let
be the angle between them. Then,
Let
and
be vectors, and let
denote the angle between them. Then
Taking square roots and noting that
for
we have the desired result:
□
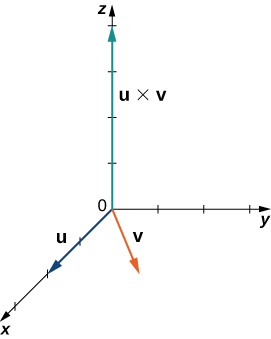
This definition of the cross product allows us to visualize or interpret the product geometrically. It is clear, for example, that the cross product is defined only for vectors in three dimensions, not for vectors in two dimensions. In two dimensions, it is impossible to generate a vector simultaneously orthogonal to two nonparallel vectors.
We have
Using [link] to find the cross product of two vectors is straightforward, and it presents the cross product in the useful component form. The formula, however, is complicated and difficult to remember. Fortunately, we have an alternative. We can calculate the cross product of two vectors using determinant notation.
A
determinant is defined by
For example,
A
determinant is defined in terms of
determinants as follows:
[link] is referred to as the expansion of the determinant along the first row. Notice that the multipliers of each of the
determinants on the right side of this expression are the entries in the first row of the
determinant. Furthermore, each of the
determinants contains the entries from the
determinant that would remain if you crossed out the row and column containing the multiplier. Thus, for the first term on the right,
is the multiplier, and the
determinant contains the entries that remain if you cross out the first row and first column of the
determinant. Similarly, for the second term, the multiplier is
and the
determinant contains the entries that remain if you cross out the first row and second column of the
determinant. Notice, however, that the coefficient of the second term is negative. The third term can be calculated in similar fashion.
Evaluate the determinant
We have
Evaluate the determinant
Expand along the first row. Don’t forget the second term is negative!
Technically, determinants are defined only in terms of arrays of real numbers. However, the determinant notation provides a useful mnemonic device for the cross product formula.
Let
and
be vectors. Then the cross product
is given by
Let
and
Find
We set up our determinant by putting the standard unit vectors across the first row, the components of
in the second row, and the components of
in the third row. Then, we have
Notice that this answer confirms the calculation of the cross product in [link].
Use determinant notation to find
where
and
Calculate the determinant
The cross product is very useful for several types of calculations, including finding a vector orthogonal to two given vectors, computing areas of triangles and parallelograms, and even determining the volume of the three-dimensional geometric shape made of parallelograms known as a parallelepiped. The following examples illustrate these calculations.
Let
and
Find a unit vector orthogonal to both
and
The cross product
is orthogonal to both vectors
and
We can calculate it with a determinant:
Normalize this vector to find a unit vector in the same direction:
Thus,
is a unit vector orthogonal to
and
Find a unit vector orthogonal to both
and
where
and
Normalize the cross product.
To use the cross product for calculating areas, we state and prove the following theorem.
If we locate vectors
and
such that they form adjacent sides of a parallelogram, then the area of the parallelogram is given by
([link]).
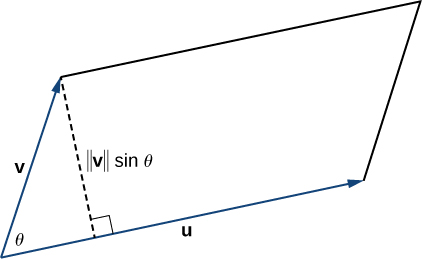
We show that the magnitude of the cross product is equal to the base times height of the parallelogram.
□
We have
and
The area of the parallelogram with adjacent sides
and
is given by
The area of
is half the area of the parallelogram, or
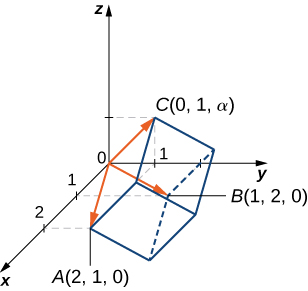
Find the area of the parallelogram
with vertices
and
Sketch the parallelogram and identify two vectors that form adjacent sides of the parallelogram.
Because the cross product of two vectors is a vector, it is possible to combine the dot product and the cross product. The dot product of a vector with the cross product of two other vectors is called the triple scalar product because the result is a scalar.
The triple scalar product of vectors
and
is
The triple scalar product of vectors
and
is the determinant of the
matrix formed by the components of the vectors:
The calculation is straightforward.
□
Let
Calculate the triple scalar product
Apply [link] directly:
Calculate the triple scalar product
where
and
Place the vectors as the rows of a
matrix, then calculate the determinant.
When we create a matrix from three vectors, we must be careful about the order in which we list the vectors. If we list them in a matrix in one order and then rearrange the rows, the absolute value of the determinant remains unchanged. However, each time two rows switch places, the determinant changes sign:
Verifying this fact is straightforward, but rather messy. Let’s take a look at this with an example:
Switching the top two rows we have
Rearranging vectors in the triple products is equivalent to reordering the rows in the matrix of the determinant. Let
and
Applying [link], we have
We can obtain the determinant for calculating
by switching the bottom two rows of
Therefore,
Following this reasoning and exploring the different ways we can interchange variables in the triple scalar product lead to the following identities:
Let
and
be two vectors in standard position. If
and
are not scalar multiples of each other, then these vectors form adjacent sides of a parallelogram. We saw in [link] that the area of this parallelogram is
Now suppose we add a third vector
that does not lie in the same plane as
and
but still shares the same initial point. Then these vectors form three edges of a parallelepiped, a three-dimensional prism with six faces that are each parallelograms, as shown in [link]. The volume of this prism is the product of the figure’s height and the area of its base. The triple scalar product of
and
provides a simple method for calculating the volume of the parallelepiped defined by these vectors.
The volume of a parallelepiped with adjacent edges given by the vectors
is the absolute value of the triple scalar product:
See [link].
Note that, as the name indicates, the triple scalar product produces a scalar. The volume formula just presented uses the absolute value of a scalar quantity.
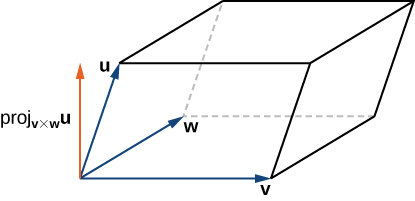
The area of the base of the parallelepiped is given by
The height of the figure is given by
The volume of the parallelepiped is the product of the height and the area of the base, so we have
□
Let
Find the volume of the parallelepiped with adjacent edges
([link]).
We have
Thus, the volume of the parallelepiped is
units3.
Find the volume of the parallelepiped formed by the vectors
and
units3
Calculate the triple scalar product by finding a determinant.
The cross product appears in many practical applications in mathematics, physics, and engineering. Let’s examine some of these applications here, including the idea of torque, with which we began this section. Other applications show up in later chapters, particularly in our study of vector fields such as gravitational and electromagnetic fields (Introduction to Vector Calculus).
Use the triple scalar product to show that vectors
are coplanar—that is, show that these vectors lie in the same plane.
Start by calculating the triple scalar product to find the volume of the parallelepiped defined by
The volume of the parallelepiped is
units3, so one of the dimensions must be zero. Therefore, the three vectors all lie in the same plane.
Are the vectors
and
coplanar?
No, the triple scalar product is
so the three vectors form the adjacent edges of a parallelepiped. They are not coplanar.
Calculate the triple scalar product.
Only a single plane can pass through any set of three noncolinear points. Find a vector orthogonal to the plane containing points
and
The plane must contain vectors
and
The cross product
produces a vector orthogonal to both
and
Therefore, the cross product is orthogonal to the plane that contains these two vectors:
We have seen how to use the triple scalar product and how to find a vector orthogonal to a plane. Now we apply the cross product to real-world situations.
Sometimes a force causes an object to rotate. For example, turning a screwdriver or a wrench creates this kind of rotational effect, called torque.
Torque,
(the Greek letter tau), measures the tendency of a force to produce rotation about an axis of rotation. Let
be a vector with an initial point located on the axis of rotation and with a terminal point located at the point where the force is applied, and let vector
represent the force. Then torque is equal to the cross product of
and
See [link].
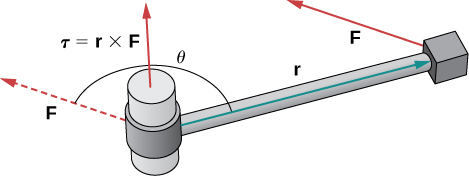
Think about using a wrench to tighten a bolt. The torque
applied to the bolt depends on how hard we push the wrench (force) and how far up the handle we apply the force (distance). The torque increases with a greater force on the wrench at a greater distance from the bolt. Common units of torque are the newton-meter or foot-pound. Although torque is dimensionally equivalent to work (it has the same units), the two concepts are distinct. Torque is used specifically in the context of rotation, whereas work typically involves motion along a line.
A bolt is tightened by applying a force of
N to a 0.15-m wrench ([link]). The angle between the wrench and the force vector is
Find the magnitude of the torque about the center of the bolt. Round the answer to two decimal places.
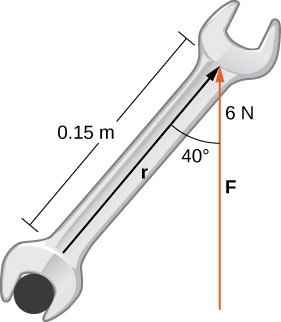
Substitute the given information into the equation defining torque:
Calculate the force required to produce
torque at an angle of
from a 150-cm rod.
N
and
of two vectors
and
is a vector orthogonal to both
and
Its length is given by
where
is the angle between
and
Its direction is given by the right-hand rule.
is
and scalar
and
is the determinant
and
form adjacent sides of a parallelogram, then the area of the parallelogram is given by
and
is
is
is zero, then the vectors are coplanar. The converse is also true: If the vectors are coplanar, then their triple scalar product is zero.
measures the tendency of a force to produce rotation about an axis of rotation. If force
is acting at a distance
from the axis, then torque is equal to the cross product of
and
For the following exercises, the vectors
and
are given.
of the vectors
and
Express the answer in component form.
and
a.
b.* * *
a.
b.* * *
Simplify
Simplify
In the following exercises, vectors
and
are given. Find unit vector
in the direction of the cross product vector
Express your answer using standard unit vectors.
where
and
where
and
Determine the real number
such that
and
are orthogonal, where
and
Show that
and
cannot be orthogonal for any
real number, where
and
Show that
is orthogonal to
and
where
and
are nonzero vectors.
Show that
is orthogonal to
where
and
are nonzero vectors.
Calculate the determinant
Calculate the determinant
For the following exercises, the vectors
and
are given. Use determinant notation to find vector
orthogonal to vectors
and
where
is a real number
where
is a nonzero real number
Find vector
where
and
Find vector
where
and
[T] Use the cross product
to find the acute angle between vectors
and
where
and
Express the answer in degrees rounded to the nearest integer.
[T] Use the cross product
to find the obtuse angle between vectors
and
where
and
Express the answer in degrees rounded to the nearest integer.
Use the sine and cosine of the angle between two nonzero vectors
and
to prove Lagrange’s identity:
Verify Lagrange’s identity
for vectors
and
Nonzero vectors
and
are called collinear if there exists a nonzero scalar
such that
Show that
and
are collinear if and only if
Nonzero vectors
and
are called collinear if there exists a nonzero scalar
such that
Show that vectors
and
are collinear, where
and
Find the area of the parallelogram with adjacent sides
and
Find the area of the parallelogram with adjacent sides
and
Consider points
and
with adjacent sides
and
to line
a.
b.
c.
Consider points
and
with adjacent sides
and
to line
In the following exercises, vectors
are given.
and
a.
b.
and
Calculate the triple scalar products
and
where
and
Calculate the triple scalar products
and
where
and
Find vectors
with a triple scalar product given by the determinant
Determine their triple scalar product.
The triple scalar product of vectors
is given by the determinant
Find vector
Consider the parallelepiped with edges
and
where
and
such that the volume of the parallelepiped is
units3.
find the height
from vertex
of the parallelepiped. Sketch the parallelepiped.
a.
b.
Consider points
and
with
and
positive real numbers.
and
(Hint: The volume of the tetrahedron is
of the volume of the parallelepiped.)
Sketch the parallelepiped and tetrahedron.
Let
be three-dimensional vectors and
be a real number. Prove the following properties of the cross product.
Show that vectors
and
satisfy the following properties of the cross product.
Nonzero vectors
are said to be linearly dependent if one of the vectors is a linear combination of the other two. For instance, there exist two nonzero real numbers
and
such that
Otherwise, the vectors are called linearly independent. Show that
are coplanar if and only if they are linear dependent.
Consider vectors
and
are coplanar by using their triple scalar product
are coplanar, using the definition that there exist two nonzero real numbers
and
such that
are linearly independent—that is, none of the vectors is a linear combination of the other two.
Consider points
and
Are vectors
and
linearly dependent (that is, one of the vectors is a linear combination of the other two)?
Yes,
where
and
Show that vectors
and
are linearly independent—that is, there exist two nonzero real numbers
and
such that
Let
and
be two-dimensional vectors. The cross product of vectors
and
is not defined. However, if the vectors are regarded as the three-dimensional vectors
and
respectively, then, in this case, we can define the cross product of
and
In particular, in determinant notation, the cross product of
and
is given by
Use this result to compute
where
is a real number.
Consider points
and
to the line passing through
Determine a vector of magnitude
perpendicular to the plane passing through the x-axis and point
Determine a unit vector perpendicular to the plane passing through the z-axis and point
Consider
and
two three-dimensional vectors. If the magnitude of the cross product vector
is
times larger than the magnitude of vector
show that the magnitude of
is greater than or equal to
where
is a natural number.
[T] Assume that the magnitudes of two nonzero vectors
and
are known. The function
defines the magnitude of the cross product vector
where
is the angle between
Interpret the results.
and
find the angle between
if the magnitude of their cross product vector is equal to
Find all vectors
that satisfy the equation
where
is any real number
Solve the equation
where
is a nonzero vector with a magnitude of
[T] A mechanic uses a 12-in. wrench to turn a bolt. The wrench makes a
angle with the horizontal. If the mechanic applies a vertical force of
lb on the wrench handle, what is the magnitude of the torque at point
(see the following figure)? Express the answer in foot-pounds rounded to two decimal places.
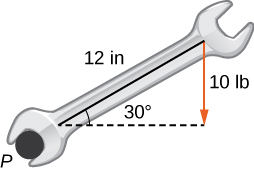
8.66 ft-lb
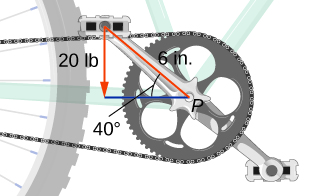
[T] A boy applies the brakes on a bicycle by applying a downward force of
lb on the pedal when the 6-in. crank makes a
angle with the horizontal (see the following figure). Find the torque at point
Express your answer in foot-pounds rounded to two decimal places.
[T] Find the magnitude of the force that needs to be applied to the end of a 20-cm wrench located on the positive direction of the y-axis if the force is applied in the direction
and it produces a
N·m torque to the bolt located at the origin.
250 N
[T] What is the magnitude of the force required to be applied to the end of a 1-ft wrench at an angle of
to produce a torque of
N·m?
[T] The force vector
acting on a proton with an electric charge of
(in coulombs) moving in a magnetic field
where the velocity vector
is given by
(here,
is expressed in meters per second,
is in tesla [T], and
is in newtons [N]). Find the force that acts on a proton that moves in the xy-plane at velocity
(in meters per second) in a magnetic field given by
[T] The force vector
acting on a proton with an electric charge of
moving in a magnetic field
where the velocity vector v is given by
(here,
is expressed in meters per second,
in
and
in
If the magnitude of force
acting on a proton is
N and the proton is moving at the speed of 300 m/sec in magnetic field
of magnitude 2.4 T, find the angle between velocity vector
of the proton and magnetic field
Express the answer in degrees rounded to the nearest integer.
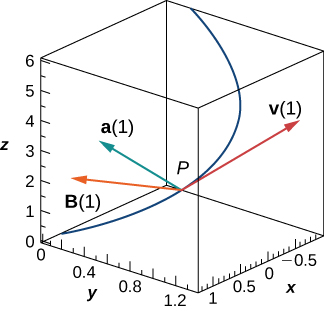
[T] Consider
the position vector of a particle at time
where the components of
are expressed in centimeters and time in seconds. Let
be the position vector of the particle after
sec.
(called the binormal unit vector) that has the direction of cross product vector
where
and
are the instantaneous velocity vector and, respectively, the acceleration vector of the particle after
seconds.
and
as vectors starting at point
along with the path of the particle.
a.
b.* * *
A solar panel is mounted on the roof of a house. The panel may be regarded as positioned at the points of coordinates (in meters)
and
(see the following figure).
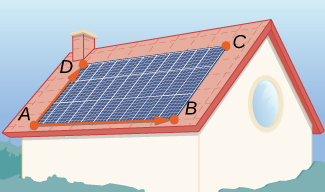
perpendicular to the surface of the solar panels. Express the answer using standard unit vectors.
points toward the Sun at a particular time of the day and the flow of solar energy is
(in watts per square meter [
]). Find the predicted amount of electrical power the panel can produce, which is given by the dot product of vectors
and
(expressed in watts).
and
and the angle of elevation are complementary.)
where
and

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: