Vectors are useful tools for solving two-dimensional problems. Life, however, happens in three dimensions. To expand the use of vectors to more realistic applications, it is necessary to create a framework for describing three-dimensional space. For example, although a two-dimensional map is a useful tool for navigating from one place to another, in some cases the topography of the land is important. Does your planned route go through the mountains? Do you have to cross a river? To appreciate fully the impact of these geographic features, you must use three dimensions. This section presents a natural extension of the two-dimensional Cartesian coordinate plane into three dimensions.
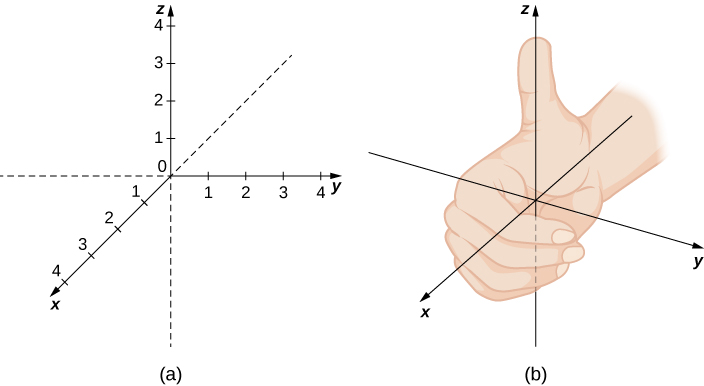
As we have learned, the two-dimensional rectangular coordinate system contains two perpendicular axes: the horizontal x-axis and the vertical y-axis. We can add a third dimension, the z-axis, which is perpendicular to both the x-axis and the y-axis. We call this system the three-dimensional rectangular coordinate system. It represents the three dimensions we encounter in real life.
The three-dimensional rectangular coordinate system consists of three perpendicular axes: the x-axis, the y-axis, and the z-axis. Because each axis is a number line representing all real numbers in
the three-dimensional system is often denoted by
In [link](a), the positive z-axis is shown above the plane containing the x- and y-axes. The positive x-axis appears to the left and the positive y-axis is to the right. A natural question to ask is: How was arrangement determined? The system displayed follows the right-hand rule. If we take our right hand and align the fingers with the positive x-axis, then curl the fingers so they point in the direction of the positive y-axis, our thumb points in the direction of the positive z-axis. In this text, we always work with coordinate systems set up in accordance with the right-hand rule. Some systems do follow a left-hand rule, but the right-hand rule is considered the standard representation.

In two dimensions, we describe a point in the plane with the coordinates
Each coordinate describes how the point aligns with the corresponding axis. In three dimensions, a new coordinate,
is appended to indicate alignment with the z-axis:
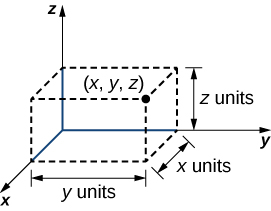
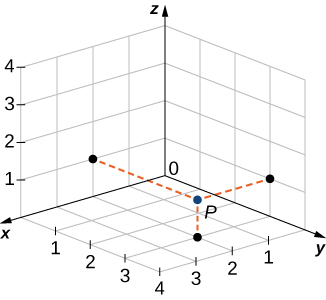
A point in space is identified by all three coordinates ([link]). To plot the point
go x units along the x-axis, then
units in the direction of the y-axis, then
units in the direction of the z-axis.
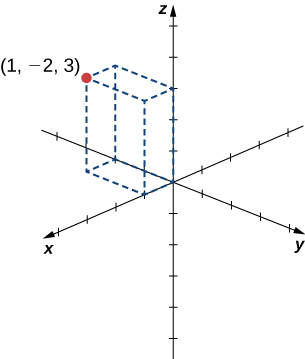
Sketch the point
in three-dimensional space.
To sketch a point, start by sketching three sides of a rectangular prism along the coordinate axes: one unit in the positive
direction,
units in the negative
direction, and
units in the positive
direction. Complete the prism to plot the point ([link]).
Sketch the point
in three-dimensional space.
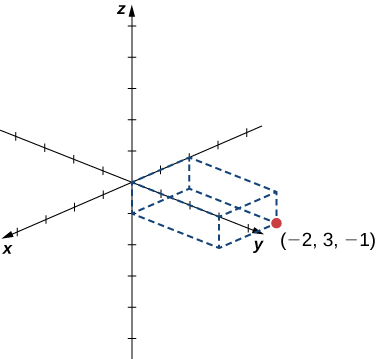
Start by sketching the coordinate axes. Then sketch a rectangular prism to help find the point in space.
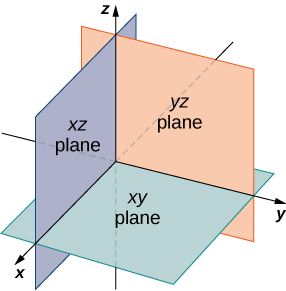
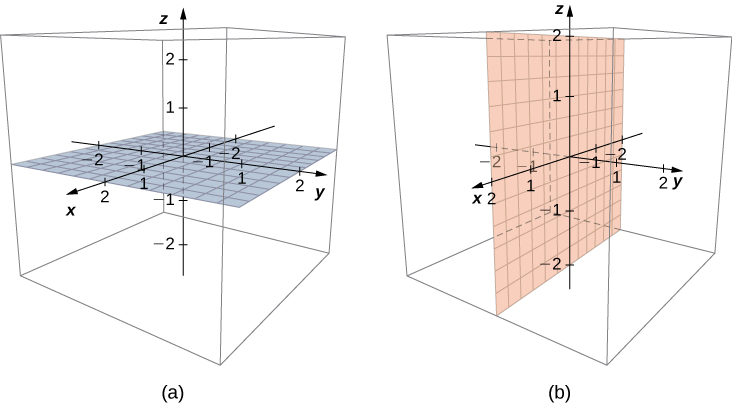
In two-dimensional space, the coordinate plane is defined by a pair of perpendicular axes. These axes allow us to name any location within the plane. In three dimensions, we define coordinate planes by the coordinate axes, just as in two dimensions. There are three axes now, so there are three intersecting pairs of axes. Each pair of axes forms a coordinate plane: the xy-plane, the xz-plane, and the yz-plane ([link]). We define the xy-plane formally as the following set:
Similarly, the xz-plane and the yz-plane are defined as
and
respectively.
To visualize this, imagine you’re building a house and are standing in a room with only two of the four walls finished. (Assume the two finished walls are adjacent to each other.) If you stand with your back to the corner where the two finished walls meet, facing out into the room, the floor is the xy-plane, the wall to your right is the xz-plane, and the wall to your left is the yz-plane.
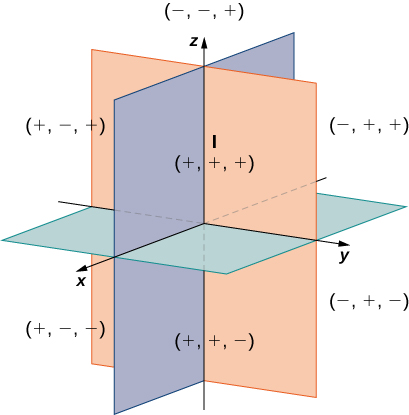
In two dimensions, the coordinate axes partition the plane into four quadrants. Similarly, the coordinate planes divide space between them into eight regions about the origin, called octants. The octants fill
in the same way that quadrants fill
as shown in [link].
Most work in three-dimensional space is a comfortable extension of the corresponding concepts in two dimensions. In this section, we use our knowledge of circles to describe spheres, then we expand our understanding of vectors to three dimensions. To accomplish these goals, we begin by adapting the distance formula to three-dimensional space.
If two points lie in the same coordinate plane, then it is straightforward to calculate the distance between them. We that the distance
between two points
and
in the xy-coordinate plane is given by the formula
The formula for the distance between two points in space is a natural extension of this formula.
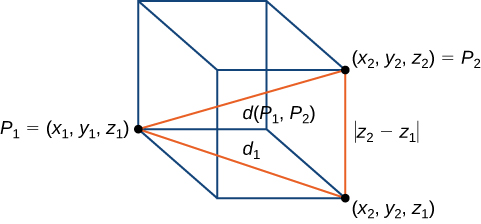
The distance
between points
and
is given by the formula
The proof of this theorem is left as an exercise. (Hint: First find the distance
between the points
and
as shown in [link].)
Find the distance between points
and
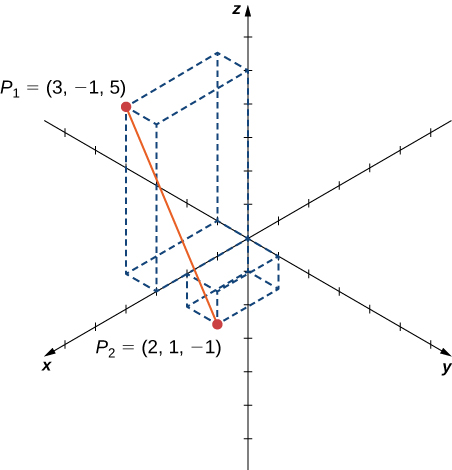
Substitute values directly into the distance formula:
Find the distance between points
and
Before moving on to the next section, let’s get a feel for how
differs from
For example, in
lines that are not parallel must always intersect. This is not the case in
For example, consider the line shown in [link]. These two lines are not parallel, nor do they intersect.
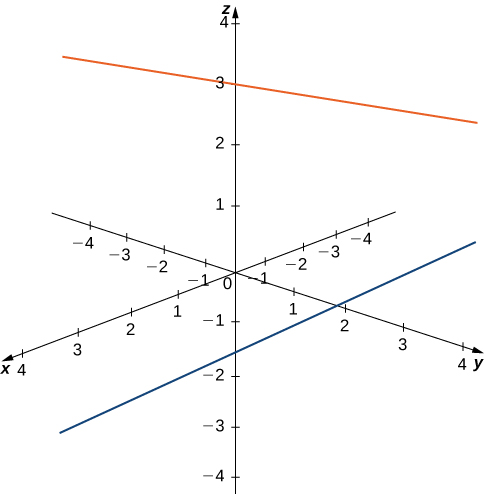
You can also have circles that are interconnected but have no points in common, as in [link].
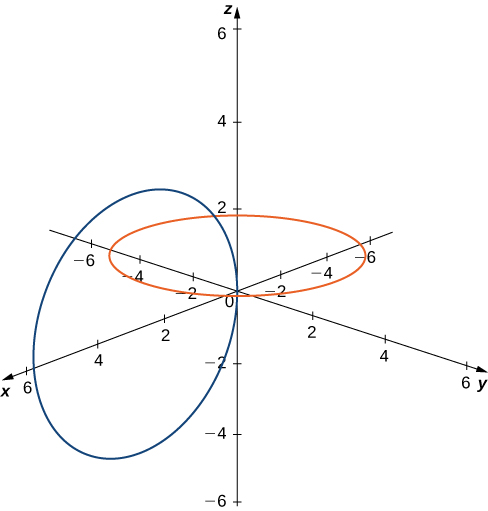
We have a lot more flexibility working in three dimensions than we do if we stuck with only two dimensions.
Now that we can represent points in space and find the distance between them, we can learn how to write equations of geometric objects such as lines, planes, and curved surfaces in
First, we start with a simple equation. Compare the graphs of the equation
in
([link]). From these graphs, we can see the same equation can describe a point, a line, or a plane.
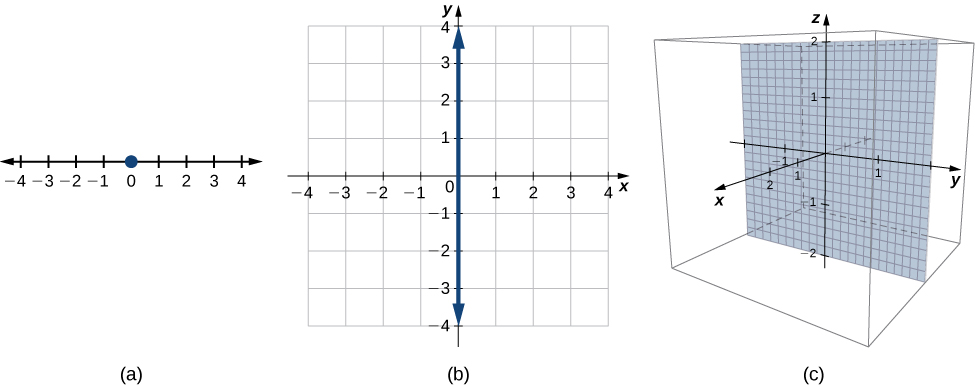
In space, the equation
describes all points
This equation defines the yz-plane. Similarly, the xy-plane contains all points of the form
The equation
defines the xy-plane and the equation
describes the xz-plane ([link]).
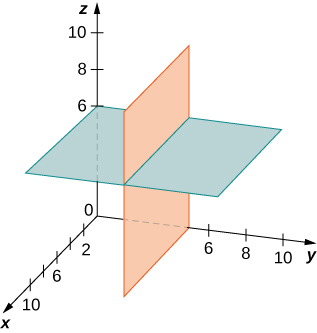
Understanding the equations of the coordinate planes allows us to write an equation for any plane that is parallel to one of the coordinate planes. When a plane is parallel to the xy-plane, for example, the z-coordinate of each point in the plane has the same constant value. Only the x- and y-coordinates of points in that plane vary from point to point.
can be represented by the equation
can be represented by the equation
can be represented by the equation
that is parallel to the yz-plane.
and
and
has the same y-coordinate. This plane can be represented by the equation
Write an equation of the plane passing through point
that is parallel to the xy-plane.
If a plane is parallel to the xy-plane, the z-coordinates of the points in that plane do not vary.
As we have seen, in
the equation
describes the vertical line passing through point
This line is parallel to the y-axis. In a natural extension, the equation
in
describes the plane passing through point
which is parallel to the yz-plane. Another natural extension of a familiar equation is found in the equation of a sphere.
A sphere is the set of all points in space equidistant from a fixed point, the center of the sphere ([link]), just as the set of all points in a plane that are equidistant from the center represents a circle. In a sphere, as in a circle, the distance from the center to a point on the sphere is called the radius.

The equation of a circle is derived using the distance formula in two dimensions. In the same way, the equation of a sphere is based on the three-dimensional formula for distance.
The sphere with center
and radius
can be represented by the equation
This equation is known as the standard equation of a sphere.
Find the standard equation of the sphere with center
and point
as shown in [link].
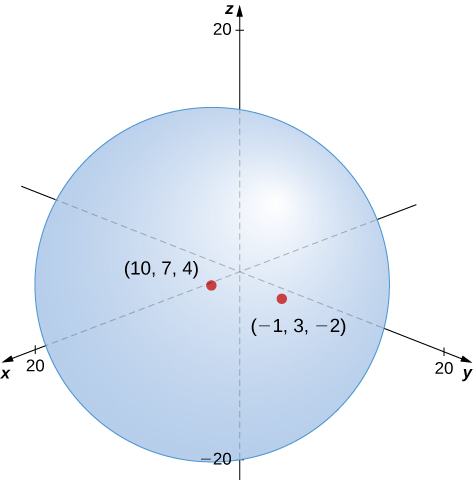
Use the distance formula to find the radius
of the sphere:
The standard equation of the sphere is
Find the standard equation of the sphere with center
containing point
First use the distance formula to find the radius of the sphere.
Let
and
and suppose line segment
forms the diameter of a sphere ([link]). Find the equation of the sphere.
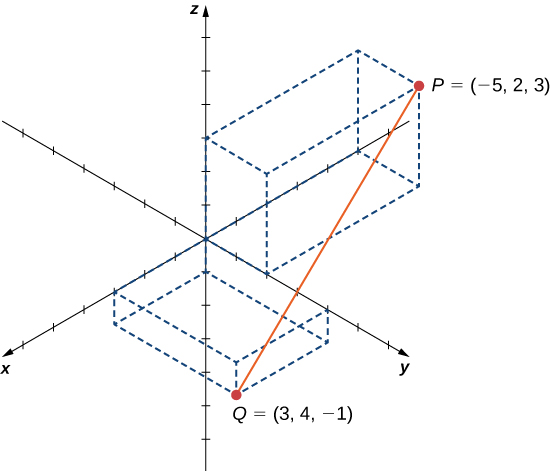
Since
is a diameter of the sphere, we know the center of the sphere is the midpoint of
Then,
Furthermore, we know the radius of the sphere is half the length of the diameter. This gives
Then, the equation of the sphere is
Find the equation of the sphere with diameter
where
and
Find the midpoint of the diameter first.
Describe the set of points that satisfies
and graph the set.
Describe the set of points that satisfies
and graph the set.
The set of points forms the two planes
and
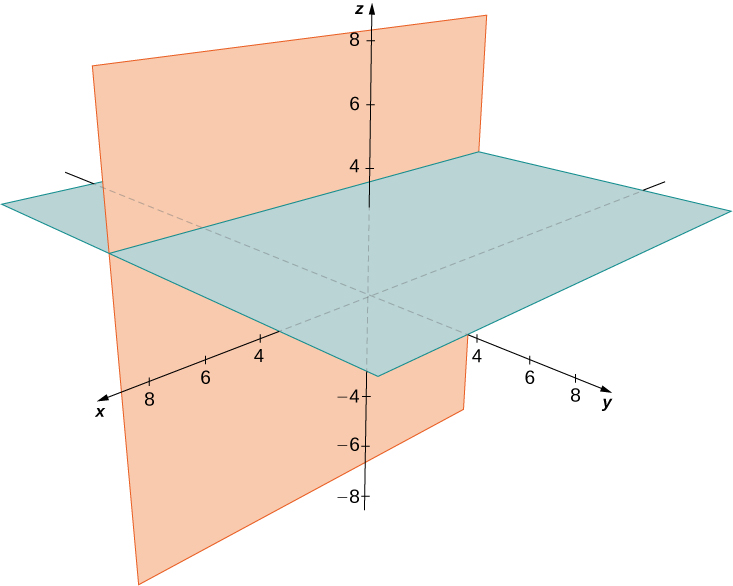
One of the factors must be zero.
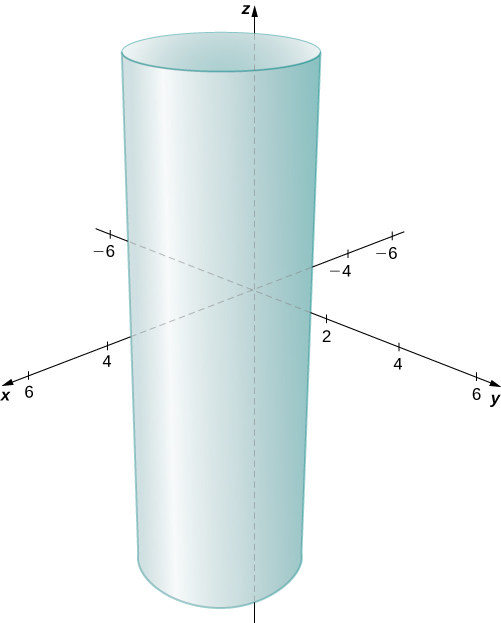
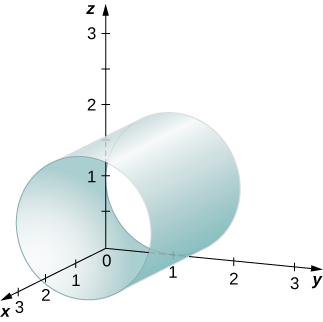
Describe the set of points in three-dimensional space that satisfies
and graph the set.
The x- and y-coordinates form a circle in the xy-plane of radius
centered at
Since there is no restriction on the z-coordinate, the three-dimensional result is a circular cylinder of radius
centered on the line with
The cylinder extends indefinitely in the z-direction ([link]).
Describe the set of points in three dimensional space that satisfies
and graph the surface.
A cylinder of radius 4 centered on the line with
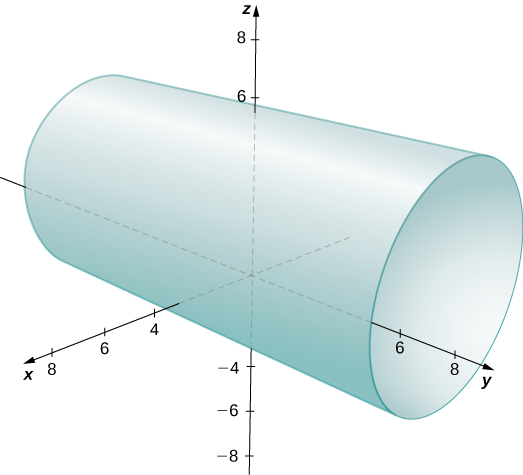
Think about what happens if you plot this equation in two dimensions in the xz-plane.
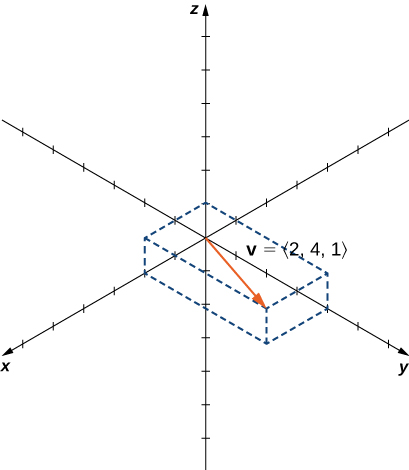
Just like two-dimensional vectors, three-dimensional vectors are quantities with both magnitude and direction, and they are represented by directed line segments (arrows). With a three-dimensional vector, we use a three-dimensional arrow.
Three-dimensional vectors can also be represented in component form. The notation
is a natural extension of the two-dimensional case, representing a vector with the initial point at the origin,
and terminal point
The zero vector is
So, for example, the three dimensional vector
is represented by a directed line segment from point
to point
([link]).
Vector addition and scalar multiplication are defined analogously to the two-dimensional case. If
and
are vectors, and
is a scalar, then
If
then
is written as
and vector subtraction is defined by
The standard unit vectors extend easily into three dimensions as well—
and
—and we use them in the same way we used the standard unit vectors in two dimensions. Thus, we can represent a vector in
in the following ways:
Let
be the vector with initial point
and terminal point
as shown in [link]. Express
in both component form and using standard unit vectors.
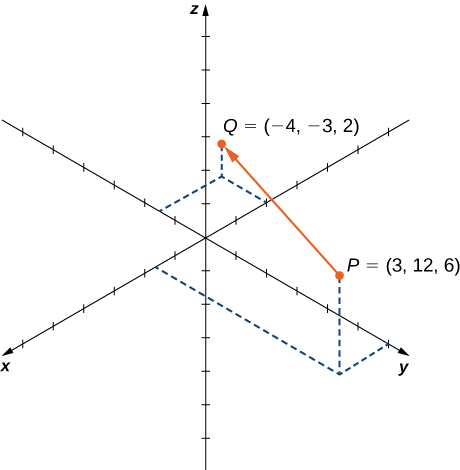
In component form,
In standard unit form,
Let
and
Express
in component form and in standard unit form.
Write
in component form first.
is the terminal point of
As described earlier, vectors in three dimensions behave in the same way as vectors in a plane. The geometric interpretation of vector addition, for example, is the same in both two- and three-dimensional space ([link]).
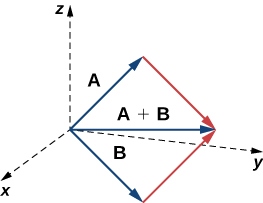
We have already seen how some of the algebraic properties of vectors, such as vector addition and scalar multiplication, can be extended to three dimensions. Other properties can be extended in similar fashion. They are summarized here for our reference.
Let
and
be vectors, and let
be a scalar.
Scalar multiplication:
Vector addition:
Vector subtraction:
Vector magnitude:
Unit vector in the direction of v:
if
We have seen that vector addition in two dimensions satisfies the commutative, associative, and additive inverse properties. These properties of vector operations are valid for three-dimensional vectors as well. Scalar multiplication of vectors satisfies the distributive property, and the zero vector acts as an additive identity. The proofs to verify these properties in three dimensions are straightforward extensions of the proofs in two dimensions.
Let
and
([link]). Find the following vectors.
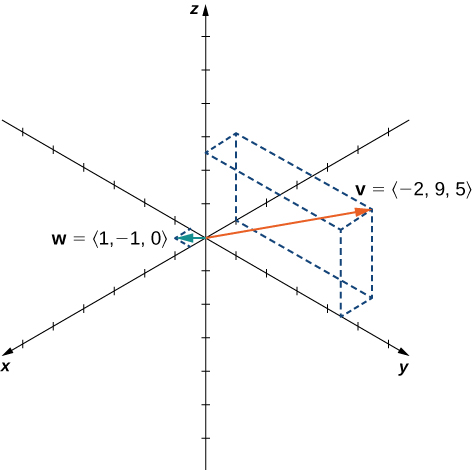
Let
and
Find a unit vector in the direction of
Start by writing
in component form.
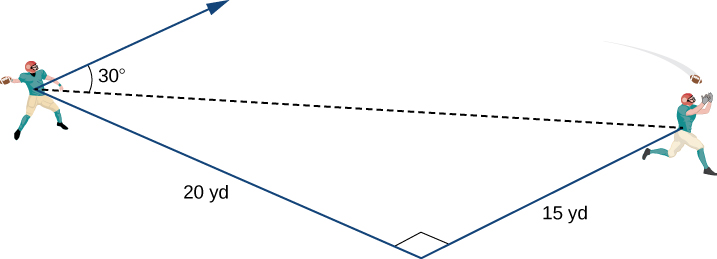
A quarterback is standing on the football field preparing to throw a pass. His receiver is standing 20 yd down the field and 15 yd to the quarterback’s left. The quarterback throws the ball at a velocity of 60 mph toward the receiver at an upward angle of
(see the following figure). Write the initial velocity vector of the ball,
in component form.
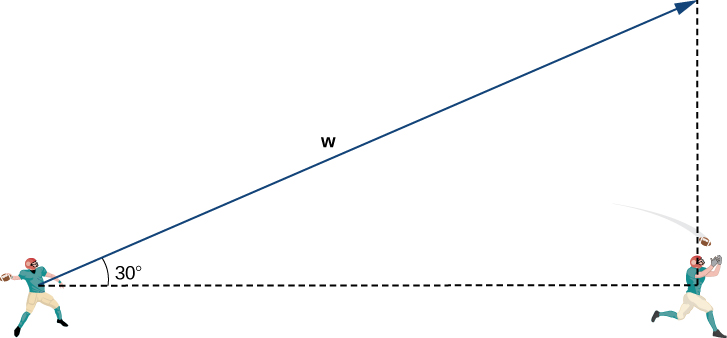
The first thing we want to do is find a vector in the same direction as the velocity vector of the ball. We then scale the vector appropriately so that it has the right magnitude. Consider the vector
extending from the quarterback’s arm to a point directly above the receiver’s head at an angle of
(see the following figure). This vector would have the same direction as
but it may not have the right magnitude.
 The receiver is 20 yd down the field and 15 yd to the quarterback’s left. Therefore, the straight-line distance from the quarterback to the receiver is
The receiver is 20 yd down the field and 15 yd to the quarterback’s left. Therefore, the straight-line distance from the quarterback to the receiver is
We have
Then the magnitude of
is given by
and the vertical distance from the receiver to the terminal point of
is
Then
and has the same direction as
Recall, though, that we calculated the magnitude of
to be
and
has magnitude
mph. So, we need to multiply vector
by an appropriate constant,
We want to find a value of
so that
mph. We have
so we want
Then
Let’s double-check that
We have
So, we have found the correct components for
Assume the quarterback and the receiver are in the same place as in the previous example. This time, however, the quarterback throws the ball at velocity of
mph and an angle of
Write the initial velocity vector of the ball,
in component form.
Follow the process used in the previous example.
are used to describe the location of a point in space.
between points
and
is given by the formula
describe planes that are parallel to the coordinate planes.
and radius
is
or in terms of the standard unit vectors,
and
be vectors, and let
be a scalar.
**Sphere with center
and radius r:**
Consider a rectangular box with one of the vertices at the origin, as shown in the following figure. If point
is the opposite vertex to the origin, then find
and
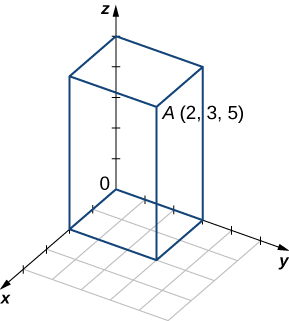
a.
b.
Find the coordinates of point
and determine its distance to the origin.
For the following exercises, describe and graph the set of points that satisfies the given equation.
A union of two planes:
(a plane parallel to the xz-plane) and
(a plane parallel to the xy-plane)* * *
A cylinder of radius
centered on the line
Write the equation of the plane passing through point
that is parallel to the xy-plane.
Write the equation of the plane passing through point
that is parallel to the xz-plane.
Find an equation of the plane passing through points
and
Find an equation of the plane passing through points
and
For the following exercises, find the equation of the sphere in standard form that satisfies the given conditions.
Center
and radius
Center
and radius
Diameter
where
and
Diameter
where
and
For the following exercises, find the center and radius of the sphere with an equation in general form that is given.
Center
and radius
For the following exercises, express vector
with the initial point at
and the terminal point at
and
a.
b.
and
and
where
is the midpoint of the line segment
a.
b.
and
where
is the midpoint of the line segment
Find terminal point
of vector
with the initial point at
Find initial point
of vector
with the terminal point at
For the following exercises, use the given vectors
and
to find and express the vectors
and
in component form.
For the following exercises, vectors u and v are given. Find the magnitudes of vectors
and
where
is a real number.
where
is a real number.
For the following exercises, find the unit vector in the direction of the given vector
and express it using standard unit vectors.
where
and
where
where
and
where
and
Determine whether
and
are equivalent vectors, where
and
Equivalent vectors
Determine whether the vectors
and
are equivalent, where
and
For the following exercises, find vector
with a magnitude that is given and satisfies the given conditions.
and
have the same direction
and
have the same direction
and
have opposite directions for any
where
is a real number
and
have opposite directions for any
where
is a real number
Determine a vector of magnitude
in the direction of vector
where
and
Find a vector of magnitude
that points in the opposite direction than vector
where
and
Express the answer in component form.
Consider the points
and
where
and
are negative real numbers. Find
and
such that
Consider points
and
where
and
are positive real numbers. Find
and
such that
Let
be a point situated at an equal distance from points
and
Show that point
lies on the plane of equation
Let
be a point situated at an equal distance from the origin and point
Show that the coordinates of point
satisfy the equation
The points
and
are collinear (in this order) if the relation
is satisfied. Show that
and
are collinear points.
Show that points
and
are not collinear.
[T] A force
of
acts on a particle in the direction of the vector
where
and the positive direction of the x-axis. Express the answer in degrees rounded to the nearest integer.
a.
b.
[T] A force
of
acts on a box in the direction of the vector
where
and the positive direction of the x-axis.
If
is a force that moves an object from point
to another point
then the displacement vector is defined as
A metal container is lifted
m vertically by a constant force
Express the displacement vector
by using standard unit vectors.
A box is pulled
yd horizontally in the x-direction by a constant force
Find the displacement vector in component form.
The sum of the forces acting on an object is called the resultant or net force. An object is said to be in static equilibrium if the resultant force of the forces that act on it is zero. Let
and
be three forces acting on a box. Find the force
acting on the box such that the box is in static equilibrium. Express the answer in component form.
[T] Let
be
forces acting on a particle, with
Express the answer using standard unit vectors.
The force of gravity
acting on an object is given by
where m is the mass of the object (expressed in kilograms) and
is acceleration resulting from gravity, with
A 2-kg disco ball hangs by a chain from the ceiling of a room.
acting on the disco ball and find its magnitude.
in the chain and its magnitude.
Express the answers using standard unit vectors.

a.
N; b.
N
A 5-kg pendant chandelier is designed such that the alabaster bowl is held by four chains of equal length, as shown in the following figure.

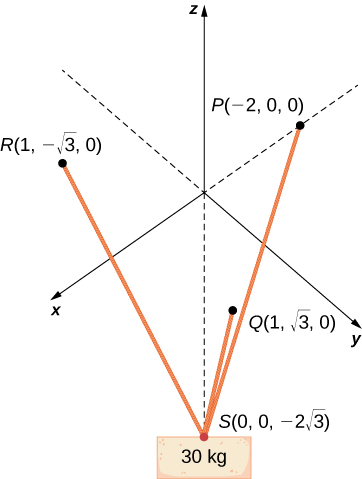
[T] A 30-kg block of cement is suspended by three cables of equal length that are anchored at points
and
The load is located at
as shown in the following figure. Let
and
be the forces of tension resulting from the load in cables
and
respectively.
acting on the block of cement that counterbalances the sum
of the forces of tension in the cables.
and
Express the answer in component form.
a.
N; b.
and
(each component is expressed in newtons)
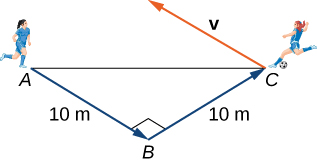
Two soccer players are practicing for an upcoming game. One of them runs 10 m from point A to point B. She then turns left at
and runs 10 m until she reaches point C. Then she kicks the ball with a speed of 10 m/sec at an upward angle of
to her teammate, who is located at point A. Write the velocity of the ball in component form.
Let
be the position vector of a particle at the time
where
and
are smooth functions on
The instantaneous velocity of the particle at time
is defined by vector
with components that are the derivatives with respect to
of the functions x, y, and z, respectively. The magnitude
of the instantaneous velocity vector is called the speed of the particle at time t. Vector
with components that are the second derivatives with respect to
of the functions
and
respectively, gives the acceleration of the particle at time
Consider
the position vector of a particle at time
where the components of
are expressed in centimeters and time is expressed in seconds.
where
a.
(each component is expressed in centimeters per second);
(expressed in centimeters per second);
(each component expressed in centimeters per second squared);
b.* * *
[T] Let
be the position vector of a particle at time
(in seconds), where
(here the components of
are expressed in centimeters).
where
describes a sphere with center
and radius
that plots its location relative to the defining axes

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: