By now, we are familiar with writing equations that describe a line in two dimensions. To write an equation for a line, we must know two points on the line, or we must know the direction of the line and at least one point through which the line passes. In two dimensions, we use the concept of slope to describe the orientation, or direction, of a line. In three dimensions, we describe the direction of a line using a vector parallel to the line. In this section, we examine how to use equations to describe lines and planes in space.
Let’s first explore what it means for two vectors to be parallel. Recall that parallel vectors must have the same or opposite directions. If two nonzero vectors,
and
are parallel, we claim there must be a scalar,
such that
If
and
have the same direction, simply choose
If
and
have opposite directions, choose
Note that the converse holds as well. If
for some scalar
then either
and
have the same direction
or opposite directions
so
and
are parallel. Therefore, two nonzero vectors
and
are parallel if and only if
for some scalar
By convention, the zero vector
is considered to be parallel to all vectors.
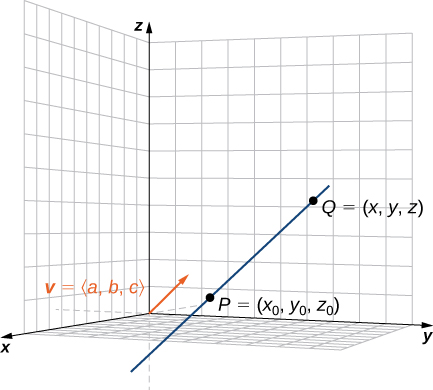
As in two dimensions, we can describe a line in space using a point on the line and the direction of the line, or a parallel vector, which we call the direction vector ([link]). Let
be a line in space passing through point
Let
be a vector parallel to
Then, for any point on line
we know that
is parallel to
Thus, as we just discussed, there is a scalar,
such that
which gives

Using vector operations, we can rewrite [link] as
Setting
and
we now have the vector equation of a line:
Equating components, [link] shows that the following equations are simultaneously true:
and
If we solve each of these equations for the component variables
we get a set of equations in which each variable is defined in terms of the parameter t and that, together, describe the line. This set of three equations forms a set of parametric equations of a line:
If we solve each of the equations for
assuming
are nonzero, we get a different description of the same line:
Because each expression equals t, they all have the same value. We can set them equal to each other to create symmetric equations of a line:
We summarize the results in the following theorem.
A line
parallel to vector
and passing through point
can be described by the following parametric equations:
If the constants
are all nonzero, then
can be described by the symmetric equation of the line:
The parametric equations of a line are not unique. Using a different parallel vector or a different point on the line leads to a different, equivalent representation. Each set of parametric equations leads to a related set of symmetric equations, so it follows that a symmetric equation of a line is not unique either.
Find parametric and symmetric equations of the line passing through points
and
First, identify a vector parallel to the line:
Use either of the given points on the line to complete the parametric equations:
Solve each equation for
to create the symmetric equation of the line:
Find parametric and symmetric equations of the line passing through points
and
Possible set of parametric equations:
related set of symmetric equations:
Start by finding a vector parallel to the line.
Sometimes we don’t want the equation of a whole line, just a line segment. In this case, we limit the values of our parameter
For example, let
and
be points on a line, and let
and
be the associated position vectors. In addition, let
We want to find a vector equation for the line segment between
and
Using
as our known point on the line, and
as the direction vector equation, [link] gives
Using properties of vectors, then
Thus, the vector equation of the line passing through
and
is
Remember that we didn’t want the equation of the whole line, just the line segment between
and
Notice that when
we have
and when
we have
Therefore, the vector equation of the line segment between
and
is
Going back to [link], we can also find parametric equations for this line segment. We have
Then, the parametric equations are
Find parametric equations of the line segment between the points
and
By [link], we have
Working with each component separately, we get
and
Therefore, the parametric equations for the line segment are
We already know how to calculate the distance between two points in space. We now expand this definition to describe the distance between a point and a line in space. Several real-world contexts exist when it is important to be able to calculate these distances. When building a home, for example, builders must consider “setback” requirements, when structures or fixtures have to be a certain distance from the property line. Air travel offers another example. Airlines are concerned about the distances between populated areas and proposed flight paths.
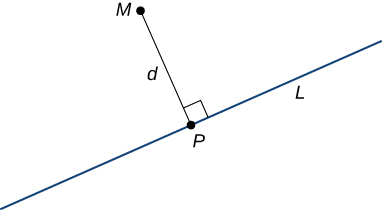
Let
be a line in the plane and let
be any point not on the line. Then, we define distance
from
to
as the length of line segment
where
is a point on
such that
is perpendicular to
([link]).
When we’re looking for the distance between a line and a point in space, [link] still applies. We still define the distance as the length of the perpendicular line segment connecting the point to the line. In space, however, there is no clear way to know which point on the line creates such a perpendicular line segment, so we select an arbitrary point on the line and use properties of vectors to calculate the distance. Therefore, let
be an arbitrary point on line
and let
be a direction vector for
([link]).
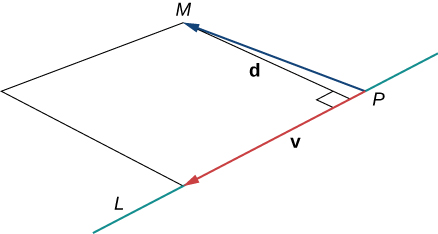
By [link], vectors
and
form two sides of a parallelogram with area
Using a formula from geometry, the area of this parallelogram can also be calculated as the product of its base and height:
We can use this formula to find a general formula for the distance between a line in space and any point not on the line.
Let
be a line in space passing through point
with direction vector
If
is any point not on
then the distance from
to
is
Find the distance between t point
and line
From the symmetric equations of the line, we know that vector
is a direction vector for the line. Setting the symmetric equations of the line equal to zero, we see that point
lies on the line. Then,
To calculate the distance, we need to find
Therefore, the distance between the point and the line is ([link])
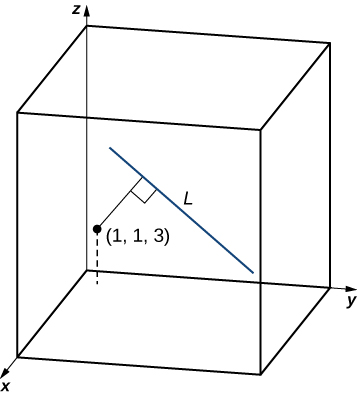
Find the distance between point
and the line with parametric equations
Find a vector with initial point
and a terminal point on the line, and then find a direction vector for the line.
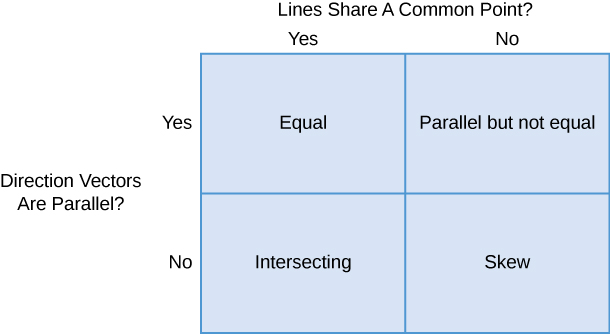
Given two lines in the two-dimensional plane, the lines are equal, they are parallel but not equal, or they intersect in a single point. In three dimensions, a fourth case is possible. If two lines in space are not parallel, but do not intersect, then the lines are said to be skew lines ([link]).
To classify lines as parallel but not equal, equal, intersecting, or skew, we need to know two things: whether the direction vectors are parallel and whether the lines share a point ([link]).
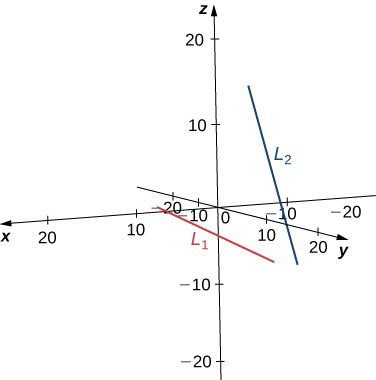
For each pair of lines, determine whether the lines are equal, parallel but not equal, skew, or intersecting.
has direction vector
line
has direction vector
Because the direction vectors are not parallel vectors, the lines are either intersecting or skew. To determine whether the lines intersect, we see if there is a point,
that lies on both lines. To find this point, we use the parametric equations to create a system of equalities:
By the first equation,
Substituting into the second equation yields
Substitution into the third equation, however, yields a contradiction:
There is no single point that satisfies the parametric equations for
simultaneously. These lines do not intersect, so they are skew (see the following figure).
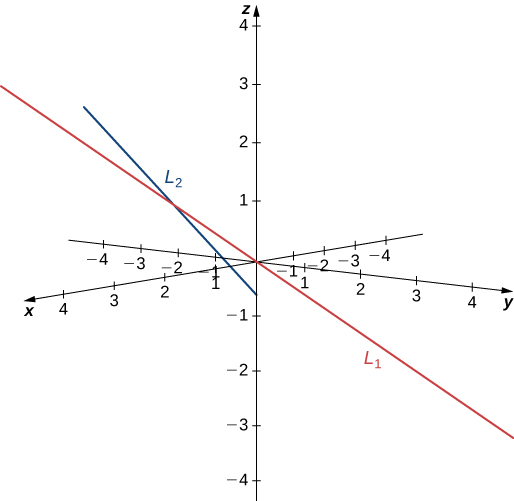
and passes through the origin,
Line
has a different direction vector,
so these lines are not parallel or equal. Let
represent the parameter for line
and let
represent the parameter for
Solve the system of equations to find
and
If we need to find the point of intersection, we can substitute these parameters into the original equations to get
(see the following figure).
and
have equivalent direction vectors:
These two lines are parallel (see the following figure).
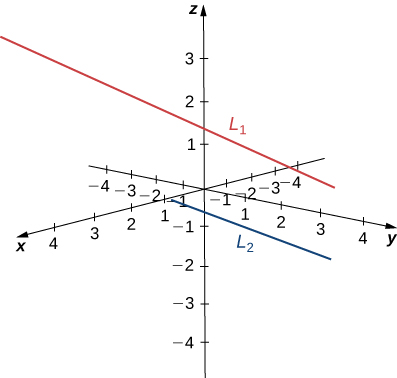
Describe the relationship between the lines with the following parametric equations:
These lines are skew because their direction vectors are not parallel and there is no point
that lies on both lines.
Start by identifying direction vectors for each line. Is one a multiple of the other?
We know that a line is determined by two points. In other words, for any two distinct points, there is exactly one line that passes through those points, whether in two dimensions or three. Similarly, given any three points that do not all lie on the same line, there is a unique plane that passes through these points. Just as a line is determined by two points, a plane is determined by three.
This may be the simplest way to characterize a plane, but we can use other descriptions as well. For example, given two distinct, intersecting lines, there is exactly one plane containing both lines. A plane is also determined by a line and any point that does not lie on the line. These characterizations arise naturally from the idea that a plane is determined by three points. Perhaps the most surprising characterization of a plane is actually the most useful.
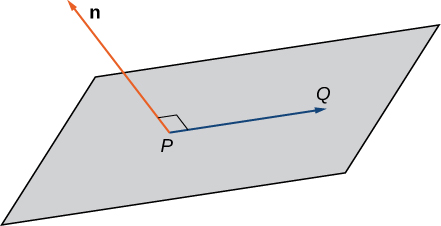
Imagine a pair of orthogonal vectors that share an initial point. Visualize grabbing one of the vectors and twisting it. As you twist, the other vector spins around and sweeps out a plane. Here, we describe that concept mathematically. Let
be a vector and
be a point. Then the set of all points
such that
is orthogonal to
forms a plane ([link]). We say that
is a normal vector, or perpendicular to the plane. Remember, the dot product of orthogonal vectors is zero. This fact generates the vector equation of a plane:
Rewriting this equation provides additional ways to describe the plane:
Given a point
and vector
the set of all points
satisfying the equation
forms a plane. The equation
is known as the vector equation of a plane.
The scalar equation of a plane containing point
with normal vector
is
This equation can be expressed as
where
This form of the equation is sometimes called the general form of the equation of a plane.
As described earlier in this section, any three points that do not all lie on the same line determine a plane. Given three such points, we can find an equation for the plane containing these points.
Write an equation for the plane containing points
and
in both standard and general forms.
To write an equation for a plane, we must find a normal vector for the plane. We start by identifying two vectors in the plane:
The cross product
is orthogonal to both
and
so it is normal to the plane that contains these two vectors:
Thus,
and we can choose any of the three given points to write an equation of the plane:
The scalar equations of a plane vary depending on the normal vector and point chosen.
Find an equation of the plane that passes through point
and contains the line given by
Symmetric equations describe the line that passes through point
parallel to vector
(see the following figure). Use this point and the given point,
to identify a second vector parallel to the plane:
Use the cross product of these vectors to identify a normal vector for the plane:
The scalar equations for the plane are
and
Find an equation of the plane containing the lines
and
or
The cross product of the lines’ direction vectors gives a normal vector for the plane.
Now that we can write an equation for a plane, we can use the equation to find the distance
between a point
and the plane. It is defined as the shortest possible distance from
to a point on the plane.
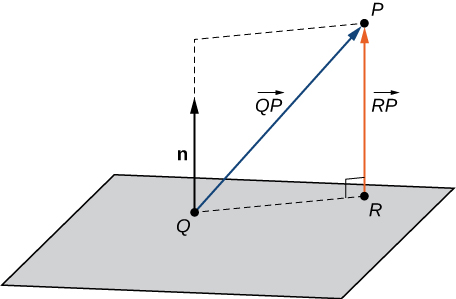
Just as we find the two-dimensional distance between a point and a line by calculating the length of a line segment perpendicular to the line, we find the three-dimensional distance between a point and a plane by calculating the length of a line segment perpendicular to the plane. Let
bet the point in the plane such that
is orthogonal to the plane, and let
be an arbitrary point in the plane. Then the projection of vector
onto the normal vector describes vector
as shown in [link].
Suppose a plane with normal vector
passes through point
The distance
from the plane to a point
not in the plane is given by
Find the distance between point
and the plane given by
(see the following figure).
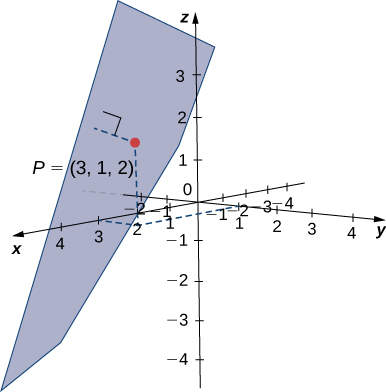
The coefficients of the plane’s equation provide a normal vector for the plane:
To find vector
we need a point in the plane. Any point will work, so set
to see that point
lies in the plane. Find the component form of the vector from
Apply the distance formula from [link]:
Find the distance between point
and the plane given by
Point
lies on the plane.
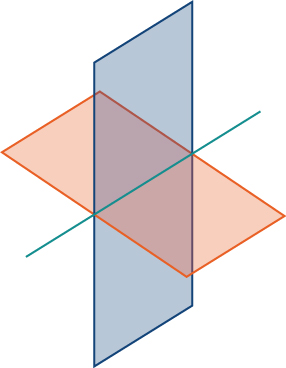
We have discussed the various possible relationships between two lines in two dimensions and three dimensions. When we describe the relationship between two planes in space, we have only two possibilities: the two distinct planes are parallel or they intersect. When two planes are parallel, their normal vectors are parallel. When two planes intersect, the intersection is a line ([link]).
We can use the equations of the two planes to find parametric equations for the line of intersection.
Find parametric and symmetric equations for the line formed by the intersection of the planes given by
and
(see the following figure).
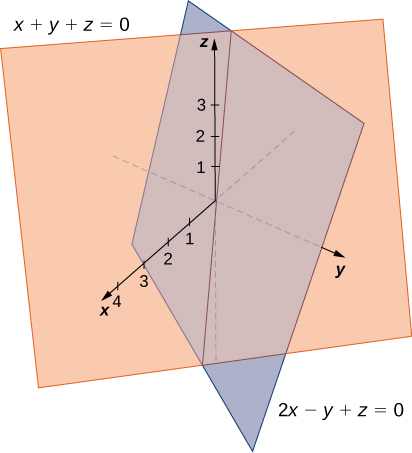
Note that the two planes have nonparallel normals, so the planes intersect. Further, the origin satisfies each equation, so we know the line of intersection passes through the origin. Add the plane equations so we can eliminate the one of the variables, in this case,
This gives us
We substitute this value into the first equation to express
in terms of
We now have the first two variables,
and
in terms of the third variable,
Now we define
in terms of
To eliminate the need for fractions, we choose to define the parameter
as
Then,
Substituting the parametric representation of
back into the other two equations, we see that the parametric equations for the line of intersection are
The symmetric equations for the line are
Find parametric equations for the line formed by the intersection of planes
and
Add the two equations, then express
in terms of
Then, express
in terms of
In addition to finding the equation of the line of intersection between two planes, we may need to find the angle formed by the intersection of two planes. For example, builders constructing a house need to know the angle where different sections of the roof meet to know whether the roof will look good and drain properly. We can use normal vectors to calculate the angle between the two planes. We can do this because the angle between the normal vectors is the same as the angle between the planes. [link] shows why this is true.
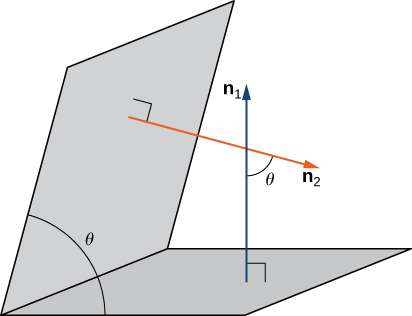
We can find the measure of the angle θ between two intersecting planes by first finding the cosine of the angle, using the following equation:
We can then use the angle to determine whether two planes are parallel or orthogonal or if they intersect at some other angle.
Determine whether each pair of planes is parallel, orthogonal, or neither. If the planes are intersecting, but not orthogonal, find the measure of the angle between them. Give the answer in radians and round to two decimal places.
and
These two vectors are scalar multiples of each other. The normal vectors are parallel, so the planes are parallel.
and
Taking the dot product of these vectors, we have
The normal vectors are orthogonal, so the corresponding planes are orthogonal as well.
and
The angle between the two planes is
rad, or approximately
Find the measure of the angle between planes
and
Give the answer in radians and round to two decimal places.
rad
Use the coefficients of the variables in each equation to find a normal vector for each plane.
When we find that two planes are parallel, we may need to find the distance between them. To find this distance, we simply select a point in one of the planes. The distance from this point to the other plane is the distance between the planes.
Previously, we introduced the formula for calculating this distance in [link]:
where
is a point on the plane,
is a point not on the plane, and
is the normal vector that passes through point
Consider the distance from point
to plane
Let
be any point in the plane. Substituting into the formula yields
We state this result formally in the following theorem.
Let
be a point. The distance from
to plane
is given by
Find the distance between the two parallel planes given by
and
Point
lies in the first plane. The desired distance, then, is
Find the distance between parallel planes
and
Set
to find a point on the first plane.
Finding the distance from a point to a line or from a line to a plane seems like a pretty abstract procedure. But, if the lines represent pipes in a chemical plant or tubes in an oil refinery or roads at an intersection of highways, confirming that the distance between them meets specifications can be both important and awkward to measure. One way is to model the two pipes as lines, using the techniques in this chapter, and then calculate the distance between them. The calculation involves forming vectors along the directions of the lines and using both the cross product and the dot product.
The symmetric forms of two lines,
and
are
You are to develop a formula for the distance
between these two lines, in terms of the values
The distance between two lines is usually taken to mean the minimum distance, so this is the length of a line segment or the length of a vector that is perpendicular to both lines and intersects both lines.
and
that lie along
and
respectively.
This vector is perpendicular to
and hence is perpendicular to both lines.
form a unit vector
in the same direction.
that lies between any two points, one on each line. Again, this can be done directly from the symmetric equations.
where
is the angle between the vectors. Using the dot product, find the projection of vector
found in step
onto unit vector
found in step 3. This projection is perpendicular to both lines, and hence its length must be the perpendicular distance
between them. Note that the value of
may be negative, depending on your choice of vector
or the order of the cross product, so use absolute value signs around the numerator.
between the following two lines:
and
What is the result of their dot product?
The rectangular frame structure has the dimensions
(height, width, and depth). One sector has a pipe entering the lower corner of the standard frame unit and exiting at the diametrically opposed corner (the one farthest away at the top); call this
A second pipe enters and exits at the two different opposite lower corners; call this
([link]).
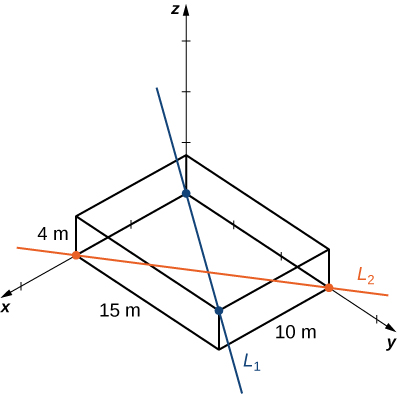
Write down the vectors along the lines representing those pipes, find the cross product between them from which to create the unit vector
define a vector that spans two points on each line, and finally determine the minimum distance between the lines. (Take the origin to be at the lower corner of the first pipe.) Similarly, you may also develop the symmetric equations for each line and substitute directly into your formula.
passing through point
is
where
is the position vector of point
This equation can be rewritten to form the parametric equations of the line:
and
The line can also be described with the symmetric equations
be a line in space passing through point
with direction vector
If
is any point not on
then the distance from
to
is
and vector
the set of all points
satisfying equation
forms a plane. Equation
is known as the vector equation of a plane.
with normal vector
is
This equation can be expressed as
where
This form of the equation is sometimes called the general form of the equation of a plane.
The distance
from the plane to point
not in the plane is given by
between two intersecting planes can be found using the equation:
where
and
are normal vectors to the planes.
from point
to plane
is given by
and
In the following exercises, points
and
are given. Let
be the line passing through points
and
and
a.
b.
c.
d.
a.
b.
c.
d.
For the following exercises, point
and vector
are given. Let
be the line passing through point
with direction
a.
b.
c.
where
and
a.
b.
c. The line does not intersect the xy-plane.
where
and
For the following exercises, line
is given.
that belongs to the line and direction vector
of the line. Express
in component form.
a.
b.
Find the distance between point
and the line of symmetric equations
Find the distance between point
and the line of parametric equations
For the following exercises, lines
and
are given.
and
are parallel.
and
are parallel, then find the distance between them.
a. Parallel; b.
Show that the line passing through points
and
is perpendicular to the line with equation
Are the lines of equations
and
perpendicular to each other?
Find the point of intersection of the lines of equations
and
Find the intersection point of the x-axis with the line of parametric equations
For the following exercises, lines
and
are given. Determine whether the lines are equal, parallel but not equal, skew, or intersecting.
and
The lines are skew.
and
and
The lines are equal.
and
Consider line
of symmetric equations
and point
that passes through point
and that passes through point
and passes through point
a.
b. For instance, the line passing through
with direction vector
c. For instance, the line passing through
and point
that belongs to
is a line that intersects;
Consider line
of parametric equations
that passes through the origin.
that passes through the origin.
and passes through the origin.
For the following exercises, point
and vector
are given.
and has normal vector
and has normal vector
a.
b.
a.
b.
For the following exercises, the equation of a plane is given.
to the plane. Express
using standard unit vectors.
[T]
a.
b.
and
c.* * *
a.
b.
c.* * *
Given point
and vector
find point
on the x-axis such that
and
are orthogonal.
Show there is no plane perpendicular to
that passes through points
and
Find parametric equations of the line passing through point
that is perpendicular to the plane of equation
Find symmetric equations of the line passing through point
that is perpendicular to the plane of equation
Show that line
is parallel to plane
Find the real number
such that the line of parametric equations
is parallel to the plane of equation
For the following exercises, points
are given.
of the plane at a., where
is an arbitrary point of the plane.
and
a.
b.
c.
and
Consider the planes of equations
and
that is parallel to the line of intersection of the planes.
a. Answers may vary; b.
Consider the planes of equations
and
that is parallel to the line of intersection of the planes.
Find the scalar equation of the plane that passes through point
and is perpendicular to the line of intersection of planes
and
Find the general equation of the plane that passes through the origin and is perpendicular to the line of intersection of planes
and
Determine whether the line of parametric equations
intersects the plane with equation
If it does intersect, find the point of intersection.
The line intersects the plane at point
Determine whether the line of parametric equations
intersects the plane with equation
If it does intersect, find the point of intersection.
Find the distance from point
to the plane of equation
Find the distance from point
to the plane of equation
For the following exercises, the equations of two planes are given.
[T]
a. The planes are neither parallel nor orthogonal; b.
a. The planes are parallel.
[T]
Show that the lines of equations
and
are skew, and find the distance between them.
Show that the lines of equations
and
are skew, and find the distance between them.
Consider point
and the plane of equation
tangent to the given plane.
a.
b.
Consider the plane of equation
at the origin that is tangent to the given plane.
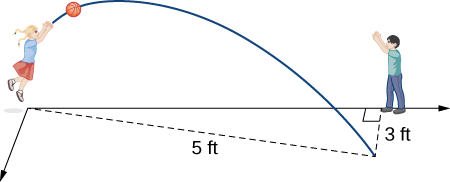
Two children are playing with a ball. The girl throws the ball to the boy. The ball travels in
the air, curves
ft to the right, and falls
ft away from the girl (see the following figure). If the plane that contains the trajectory of the ball is perpendicular to the ground, find its equation.
[T] John allocates
dollars to consume monthly three goods of prices
In this context, the budget equation is defined as
where
and
represent the number of items bought from each of the goods. The budget set is given by
and the budget plane is the part of the plane of equation
for which
and
Consider
and
find the new budget equation and graph the budget set in the same system of coordinates.
[T] Consider
the position vector of a particle at time
where the components of r are expressed in centimeters and time is measured in seconds. Let
be the position vector of the particle after
sec.
of the particle after
sec.
and passes through point
This plane is called the normal plane to the path of the particle at point
a.
b.
c.* * *
[T] A solar panel is mounted on the roof of a house. The panel may be regarded as positioned at the points of coordinates (in meters)
and
(see the following figure).
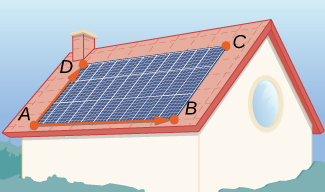
and show that its normal vector is equivalent to
that passes through the center of the solar panel and has direction vector
which points toward the position of the Sun at a particular time of day.
that passes through the center of the solar panel and is perpendicular to it.
and
where
is a normal vector of the plane,
is a point on the plane, and
and
describing the line with direction vector
passing through point
used to describe a plane containing point
with normal vector
or its alternate form
where
symmetric equations of
describing the line with direction vector
passing through point
used to describe a line with direction vector
passing through point
where
is the position vector of point
where
is a given point in the plane,
is any point in the plane, and
is a normal vector of the plane

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: