The rectangular coordinate system (or Cartesian plane) provides a means of mapping points to ordered pairs and ordered pairs to points. This is called a one-to-one mapping from points in the plane to ordered pairs. The polar coordinate system provides an alternative method of mapping points to ordered pairs. In this section we see that in some circumstances, polar coordinates can be more useful than rectangular coordinates.
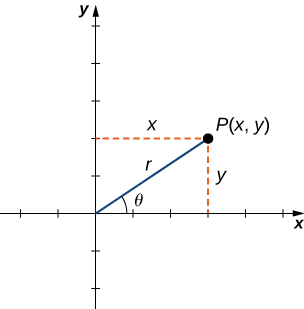
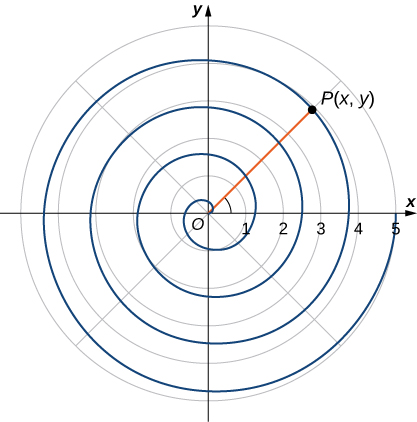
To find the coordinates of a point in the polar coordinate system, consider [link]. The point
has Cartesian coordinates
The line segment connecting the origin to the point
measures the distance from the origin to
and has length
The angle between the positive
-axis and the line segment has measure
This observation suggests a natural correspondence between the coordinate pair
and the values
and
This correspondence is the basis of the polar coordinate system. Note that every point in the Cartesian plane has two values (hence the term ordered pair) associated with it. In the polar coordinate system, each point also two values associated with it:
and

Using right-triangle trigonometry, the following equations are true for the point
Furthermore,
Each point
in the Cartesian coordinate system can therefore be represented as an ordered pair
in the polar coordinate system. The first coordinate is called the radial coordinate and the second coordinate is called the angular coordinate. Every point in the plane can be represented in this form.
Note that the equation
has an infinite number of solutions for any ordered pair
However, if we restrict the solutions to values between
and
then we can assign a unique solution to the quadrant in which the original point
is located. Then the corresponding value of r is positive, so
Given a point
in the plane with Cartesian coordinates
and polar coordinates
the following conversion formulas hold true:
These formulas can be used to convert from rectangular to polar or from polar to rectangular coordinates.
Convert each of the following points into polar coordinates.
Convert each of the following points into rectangular coordinates.
and
in [link]:
Therefore this point can be represented as
in polar coordinates.
and
in [link]:
Therefore this point can be represented as
in polar coordinates.
and
in [link]:
Direct application of the second equation leads to division by zero. Graphing the point
on the rectangular coordinate system reveals that the point is located on the positive y-axis. The angle between the positive x-axis and the positive y-axis is
Therefore this point can be represented as
in polar coordinates.
and
in [link]:
Therefore this point can be represented as
in polar coordinates.
and
in [link]:
Therefore this point can be represented as
in rectangular coordinates.
and
in [link]:
Therefore this point can be represented as
in rectangular coordinates.
and
in [link]:
Therefore this point can be represented as
in rectangular coordinates.
The polar representation of a point is not unique. For example, the polar coordinates
and
both represent the point
in the rectangular system. Also, the value of
can be negative. Therefore, the point with polar coordinates
also represents the point
in the rectangular system, as we can see by using [link]:
Every point in the plane has an infinite number of representations in polar coordinates. However, each point in the plane has only one representation in the rectangular coordinate system.
Note that the polar representation of a point in the plane also has a visual interpretation. In particular,
is the directed distance that the point lies from the origin, and
measures the angle that the line segment from the origin to the point makes with the positive
-axis. Positive angles are measured in a counterclockwise direction and negative angles are measured in a clockwise direction. The polar coordinate system appears in the following figure.
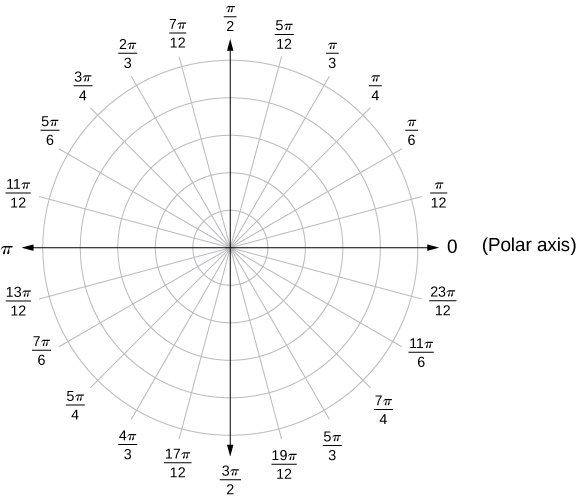
The line segment starting from the center of the graph going to the right (called the positive x-axis in the Cartesian system) is the polar axis. The center point is the pole, or origin, of the coordinate system, and corresponds to
The innermost circle shown in [link] contains all points a distance of 1 unit from the pole, and is represented by the equation
Then
is the set of points 2 units from the pole, and so on. The line segments emanating from the pole correspond to fixed angles. To plot a point in the polar coordinate system, start with the angle. If the angle is positive, then measure the angle from the polar axis in a counterclockwise direction. If it is negative, then measure it clockwise. If the value of
is positive, move that distance along the terminal ray of the angle. If it is negative, move along the ray that is opposite the terminal ray of the given angle.
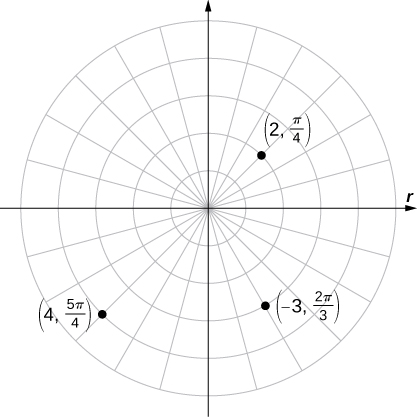
Plot each of the following points on the polar plane.
The three points are plotted in the following figure.
Plot
and
on the polar plane.
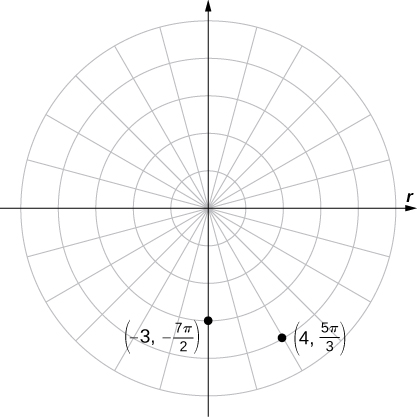
Start with
then use
Now that we know how to plot points in the polar coordinate system, we can discuss how to plot curves. In the rectangular coordinate system, we can graph a function
and create a curve in the Cartesian plane. In a similar fashion, we can graph a curve that is generated by a function
The general idea behind graphing a function in polar coordinates is the same as graphing a function in rectangular coordinates. Start with a list of values for the independent variable
in this case) and calculate the corresponding values of the dependent variable
This process generates a list of ordered pairs, which can be plotted in the polar coordinate system. Finally, connect the points, and take advantage of any patterns that may appear. The function may be periodic, for example, which indicates that only a limited number of values for the independent variable are needed.
and the second column is for
values for each
on the coordinate axes.
Watch this video for more information on sketching polar curves.
Graph the curve defined by the function
Identify the curve and rewrite the equation in rectangular coordinates.
Because the function is a multiple of a sine function, it is periodic with period
so use values for
between 0 and
The result of steps 1–3 appear in the following table. [link] shows the graph based on this table.
| 0 | 0 | 0 | ||
| 0 |
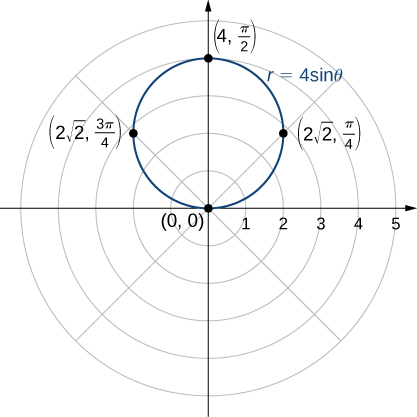
This is the graph of a circle. The equation
can be converted into rectangular coordinates by first multiplying both sides by
This gives the equation
Next use the facts that
and
This gives
To put this equation into standard form, subtract
from both sides of the equation and complete the square:
This is the equation of a circle with radius 2 and center
in the rectangular coordinate system.
Create a graph of the curve defined by the function
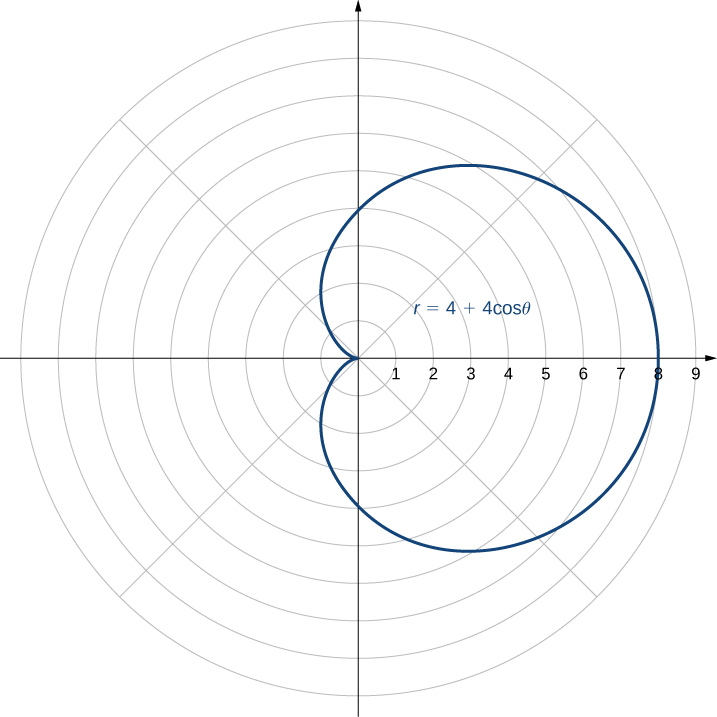
The name of this shape is a cardioid, which we will study further later in this section.
Follow the problem-solving strategy for creating a graph in polar coordinates.
The graph in [link] was that of a circle. The equation of the circle can be transformed into rectangular coordinates using the coordinate transformation formulas in [link]. [link] gives some more examples of functions for transforming from polar to rectangular coordinates.
Rewrite each of the following equations in rectangular coordinates and identify the graph.
Since
we can replace the left-hand side of this equation by
This gives
which can be rewritten as
This is the equation of a straight line passing through the origin with slope
In general, any polar equation of the form
represents a straight line through the pole with slope equal to
Next replace
with
This gives the equation
which is the equation of a circle centered at the origin with radius 3. In general, any polar equation of the form
where k is a positive constant represents a circle of radius k centered at the origin. (Note: when squaring both sides of an equation it is possible to introduce new points unintentionally. This should always be taken into consideration. However, in this case we do not introduce new points. For example,
is the same point as
This leads to
Next use the formulas
This gives
To put this equation into standard form, first move the variables from the right-hand side of the equation to the left-hand side, then complete the square.
This is the equation of a circle with center at
and radius 5. Notice that the circle passes through the origin since the center is 5 units away.
Rewrite the equation
in rectangular coordinates and identify its graph.
which is the equation of a parabola opening upward.
Convert to sine and cosine, then multiply both sides by cosine.
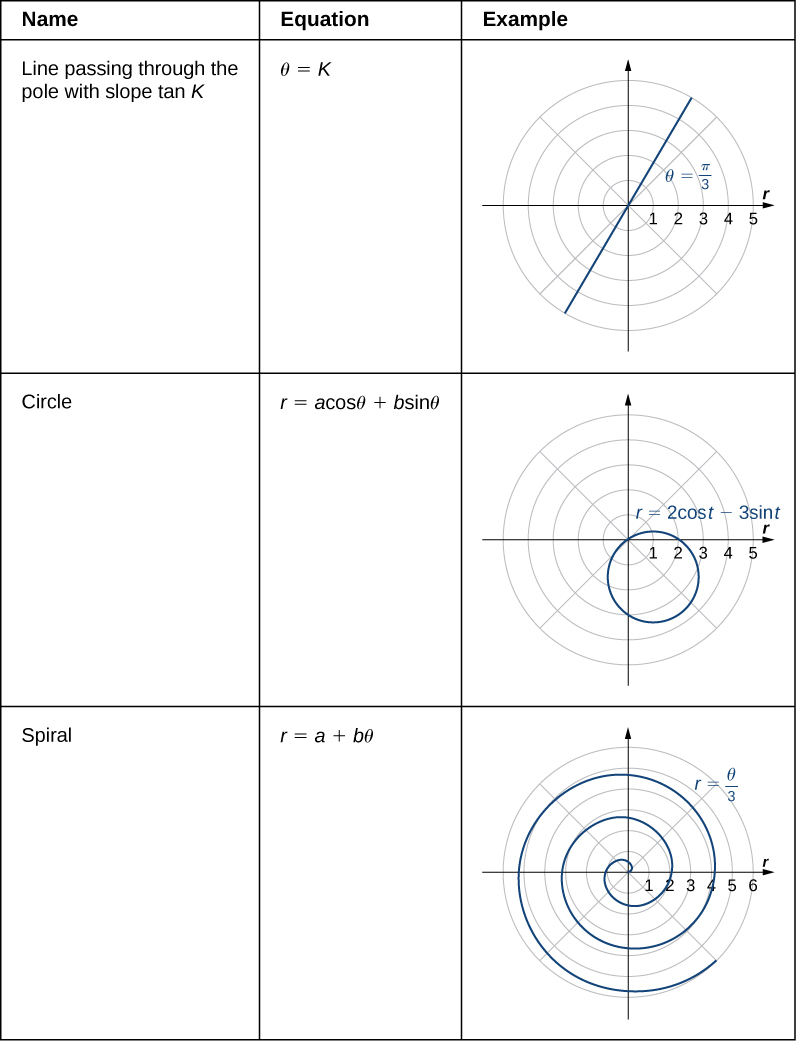
We have now seen several examples of drawing graphs of curves defined by polar equations. A summary of some common curves is given in the tables below. In each equation, a and b are arbitrary constants.
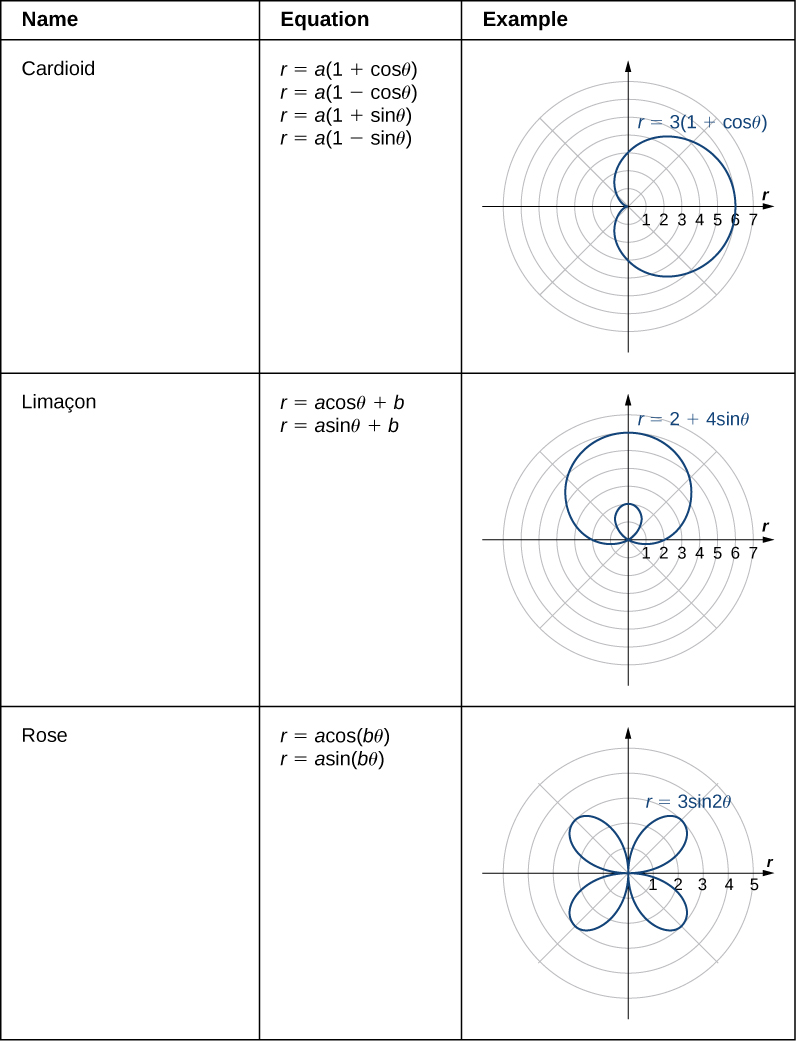
A cardioid is a special case of a limaçon (pronounced “lee-mah-son”), in which
or
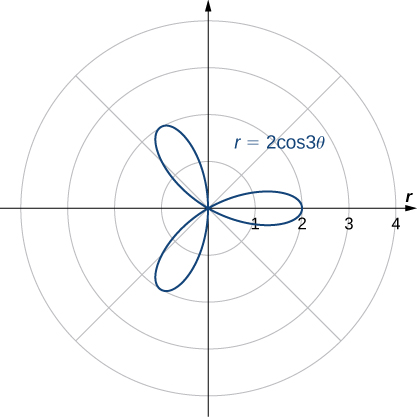
The rose is a very interesting curve. Notice that the graph of
has four petals. However, the graph of
has three petals as shown.
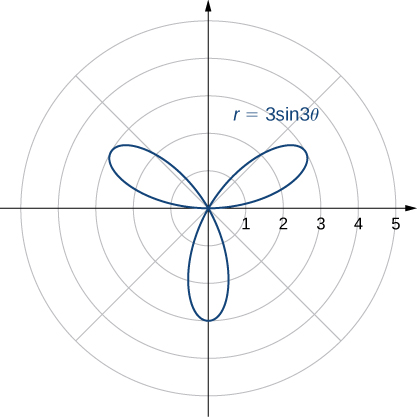
If the coefficient of
is even, the graph has twice as many petals as the coefficient. If the coefficient of
is odd, then the number of petals equals the coefficient. You are encouraged to explore why this happens. Even more interesting graphs emerge when the coefficient of
is not an integer. For example, if it is rational, then the curve is closed; that is, it eventually ends where it started ([link](a)). However, if the coefficient is irrational, then the curve never closes ([link](b)). Although it may appear that the curve is closed, a closer examination reveals that the petals just above the positive x axis are slightly thicker. This is because the petal does not quite match up with the starting point.
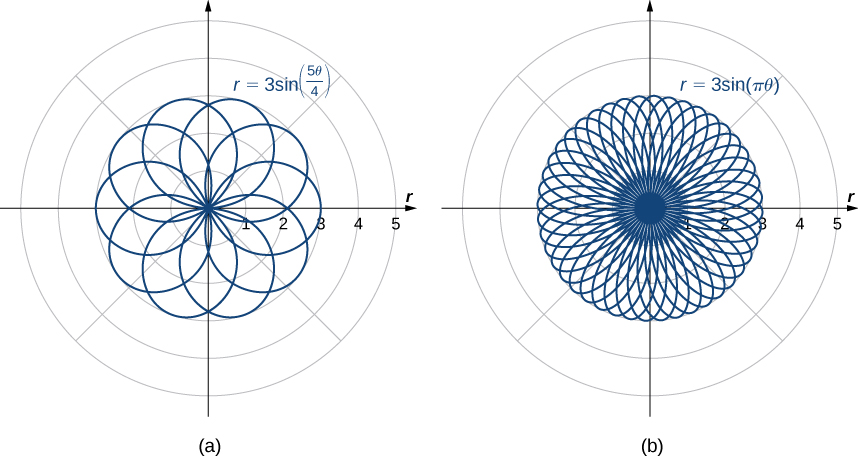
Since the curve defined by the graph of
never closes, the curve depicted in [link](b) is only a partial depiction. In fact, this is an example of a space-filling curve. A space-filling curve is one that in fact occupies a two-dimensional subset of the real plane. In this case the curve occupies the circle of radius 3 centered at the origin.
Recall the chambered nautilus introduced in the chapter opener. This creature displays a spiral when half the outer shell is cut away. It is possible to describe a spiral using rectangular coordinates. [link] shows a spiral in rectangular coordinates. How can we describe this curve mathematically?
As the point P travels around the spiral in a counterclockwise direction, its distance d from the origin increases. Assume that the distance d is a constant multiple k of the angle
that the line segment OP makes with the positive x-axis. Therefore
where
is the origin. Now use the distance formula and some trigonometry:
Although this equation describes the spiral, it is not possible to solve it directly for either x or y. However, if we use polar coordinates, the equation becomes much simpler. In particular,
and
is the second coordinate. Therefore the equation for the spiral becomes
Note that when
we also have
so the spiral emanates from the origin. We can remove this restriction by adding a constant to the equation. Then the equation for the spiral becomes
for arbitrary constants
and
This is referred to as an Archimedean spiral, after the Greek mathematician Archimedes.
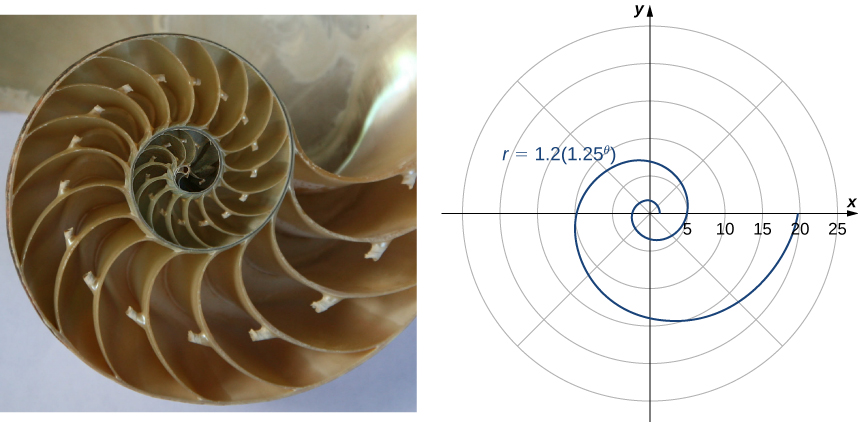
Another type of spiral is the logarithmic spiral, described by the function
A graph of the function
is given in [link]. This spiral describes the shell shape of the chambered nautilus.
Suppose a curve is described in the polar coordinate system via the function
Since we have conversion formulas from polar to rectangular coordinates given by
it is possible to rewrite these formulas using the function
This step gives a parameterization of the curve in rectangular coordinates using
as the parameter. For example, the spiral formula
from [link] becomes
Letting
range from
to
generates the entire spiral.
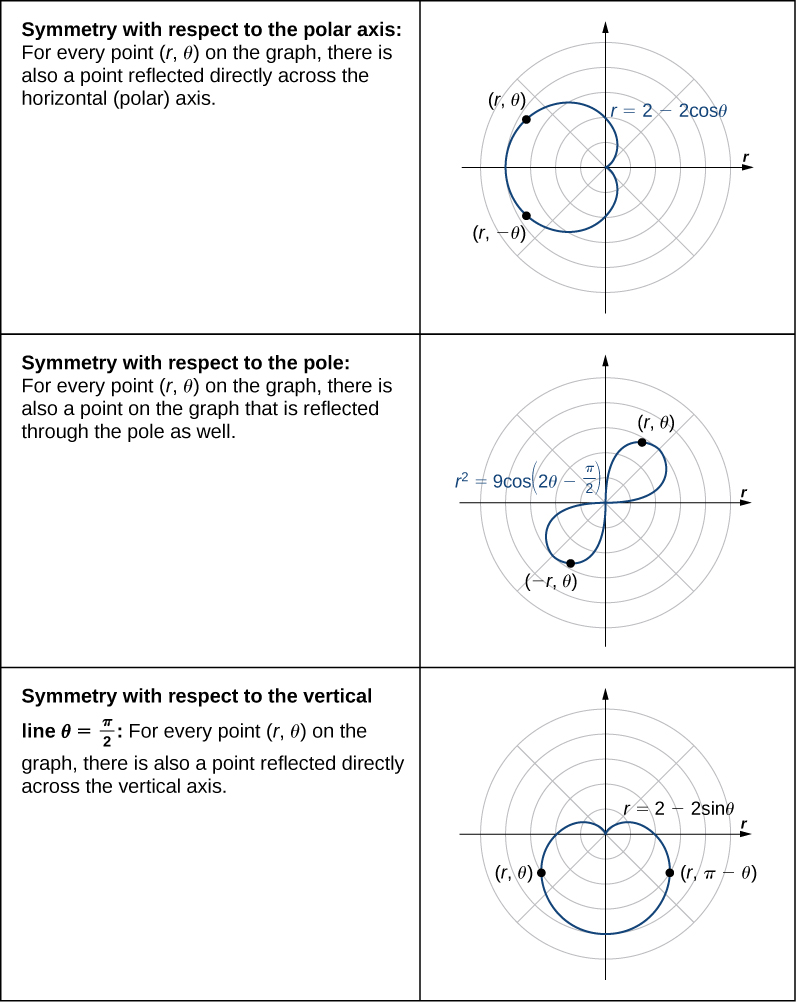
When studying symmetry of functions in rectangular coordinates (i.e., in the form
we talk about symmetry with respect to the y-axis and symmetry with respect to the origin. In particular, if
for all
in the domain of
then
is an even function and its graph is symmetric with respect to the y-axis. If
for all
in the domain of
then
is an odd function and its graph is symmetric with respect to the origin. By determining which types of symmetry a graph exhibits, we can learn more about the shape and appearance of the graph. Symmetry can also reveal other properties of the function that generates the graph. Symmetry in polar curves works in a similar fashion.
Consider a curve generated by the function
in polar coordinates.
on the graph, the point
is also on the graph. Similarly, the equation
is unchanged by replacing
with
on the graph, the point
is also on the graph. Similarly, the equation
is unchanged when replacing
with
or
with
if for every point
on the graph, the point
is also on the graph. Similarly, the equation
is unchanged when
is replaced by
The following table shows examples of each type of symmetry.
 <div data-type="example">
<div data-type="example">
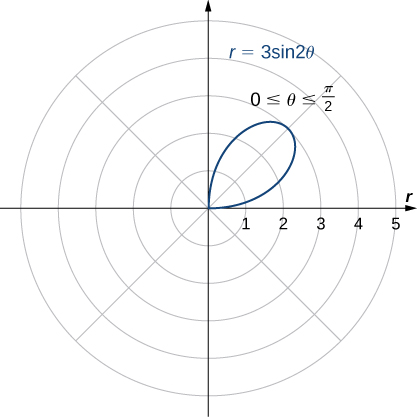
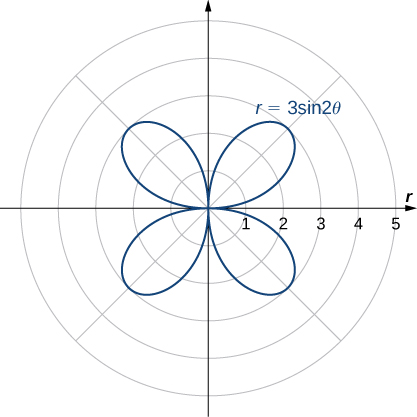
Find the symmetry of the rose defined by the equation
and create a graph.
Suppose the point
is on the graph of
with
This gives
Since this changes the original equation, this test is not satisfied. However, returning to the original equation and replacing
with
and
with
yields
Multiplying both sides of this equation by
gives
which is the original equation. This demonstrates that the graph is symmetric with respect to the polar axis.
with
which yields
Multiplying both sides by −1 gives
which does not agree with the original equation. Therefore the equation does not pass the test for this symmetry. However, returning to the original equation and replacing
with
gives
Since this agrees with the original equation, the graph is symmetric about the pole.
first replace both
with
and
with
Multiplying both sides of this equation by
gives
which is the original equation. Therefore the graph is symmetric about the vertical line
This graph has symmetry with respect to the polar axis, the origin, and the vertical line going through the pole. To graph the function, tabulate values of
between 0 and
and then reflect the resulting graph.
| {: valign=”top”} | ———- |
| {: valign=”top”} |
| {: valign=”top”} |
| {: valign=”top”} |
| {: valign=”top”} |
| {: valign=”top”}{: .unnumbered summary=”This table has two columns and six rows. The first row is a header row, and it reads from left to right θ and r. Below the header row, in the first column, the values read 0, π/6, π/4, π/3, and π/2. In the second column, the values read 0, (3 times the square root of 3) all divided by 2, which is approximately equal to 2.6, 3, (3 times the square root of 3) all divided by 2, which is approximately equal to 2.6, and 0.” data-label=””}
This gives one petal of the rose, as shown in the following graph.
Reflecting this image into the other three quadrants gives the entire graph as shown.
</div>
Determine the symmetry of the graph determined by the equation
and create a graph.
Symmetric with respect to the polar axis.* * *
Use [link].
and
In the following exercises, plot the point whose polar coordinates are given by first constructing the angle
and then marking off the distance r along the ray.
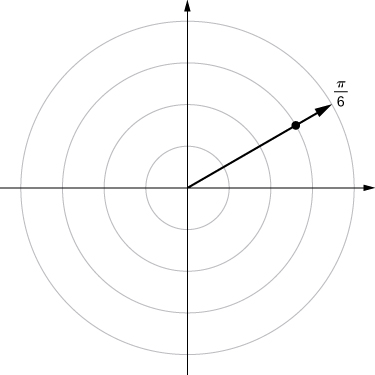
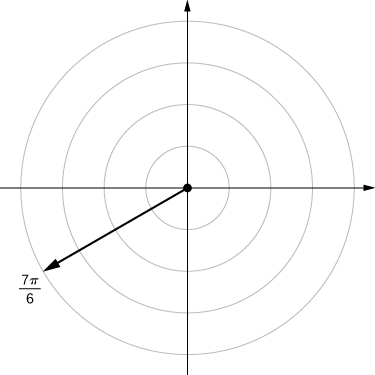
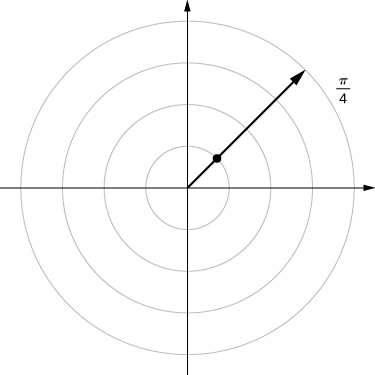
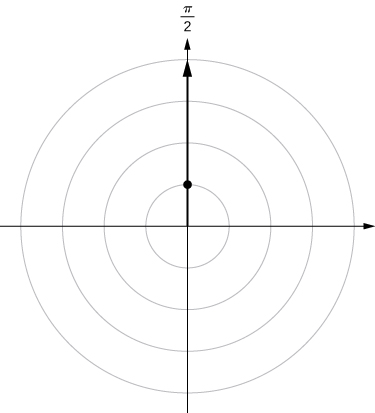
For the following exercises, consider the polar graph below. Give two sets of polar coordinates for each point.
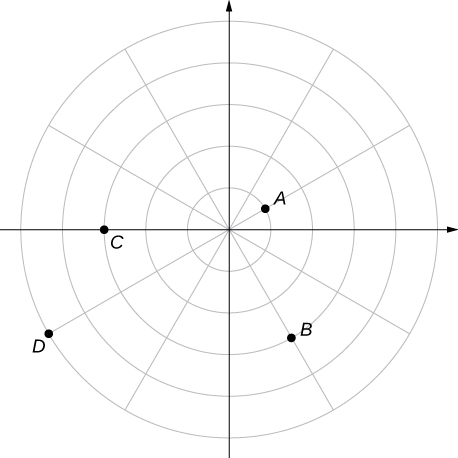
Coordinates of point A.
Coordinates of point B.
Coordinates of point C.
Coordinates of point D.
For the following exercises, the rectangular coordinates of a point are given. Find two sets of polar coordinates for the point in
Round to three decimal places.
(3, −4)
For the following exercises, find rectangular coordinates for the given point in polar coordinates.
For the following exercises, determine whether the graphs of the polar equation are symmetric with respect to the
-axis, the
-axis, or the origin.
Symmetry with respect to the x-axis, y-axis, and origin.
Symmetric with respect to x-axis only.
Symmetry with respect to x-axis only.
For the following exercises, describe the graph of each polar equation. Confirm each description by converting into a rectangular equation.
Line
For the following exercises, convert the rectangular equation to polar form and sketch its graph.
Hyperbola; polar form
or
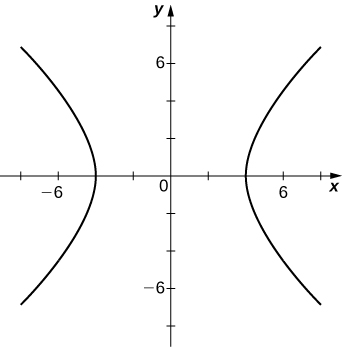
For the following exercises, convert the rectangular equation to polar form and sketch its graph.
For the following exercises, convert the polar equation to rectangular form and sketch its graph.
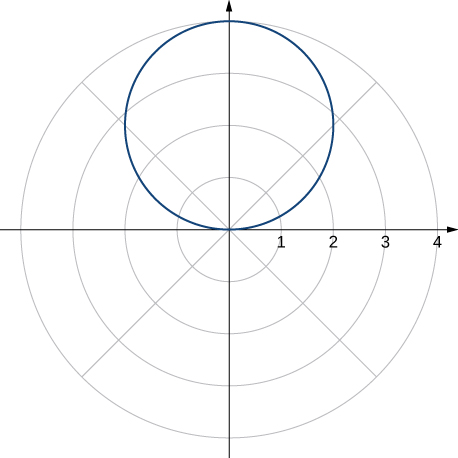
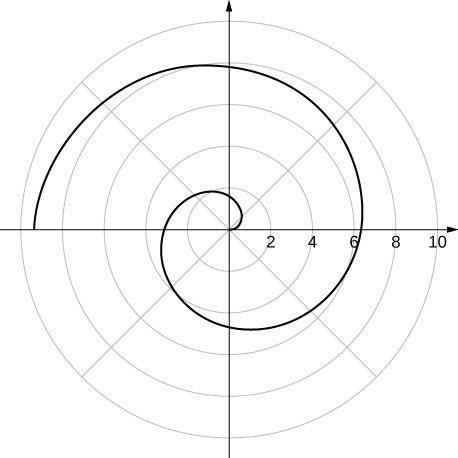
For the following exercises, sketch a graph of the polar equation and identify any symmetry.
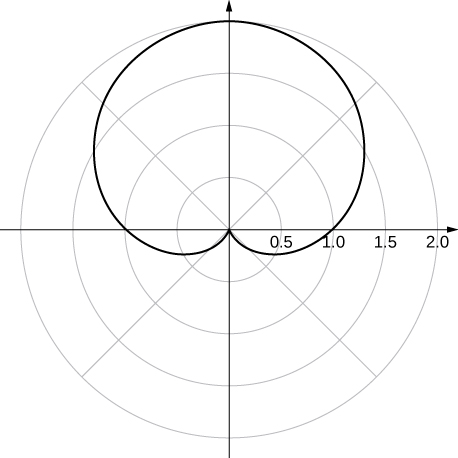
y-axis symmetry
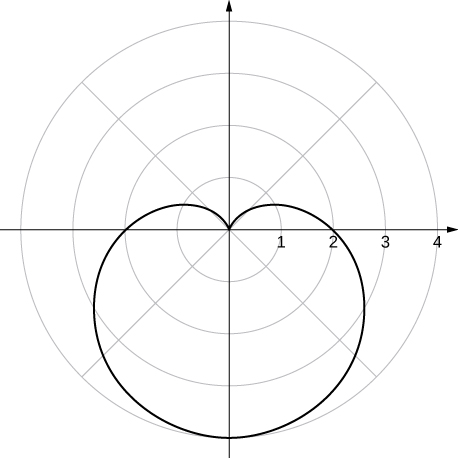
y-axis symmetry
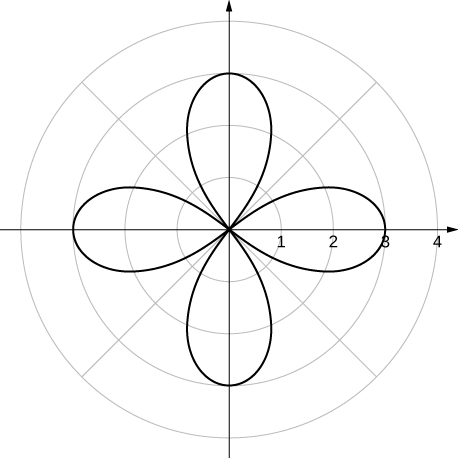
x- and y-axis symmetry and symmetry about the pole
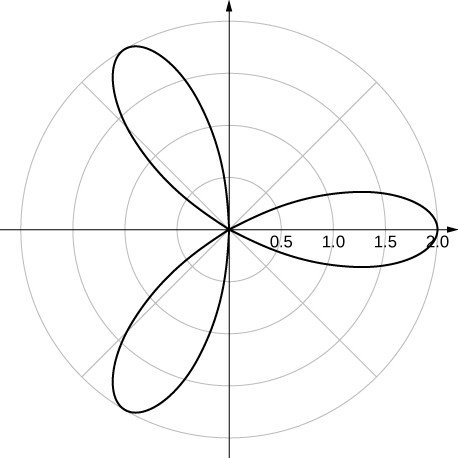
x-axis symmetry
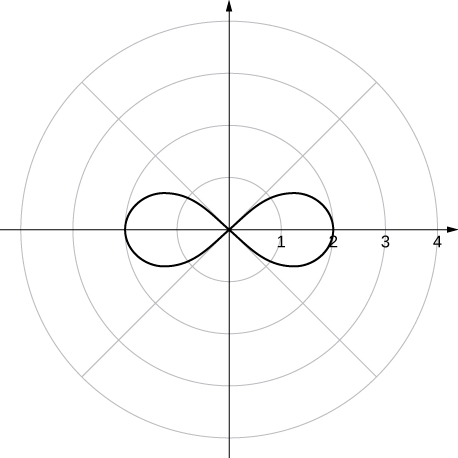
x- and y-axis symmetry and symmetry about the pole
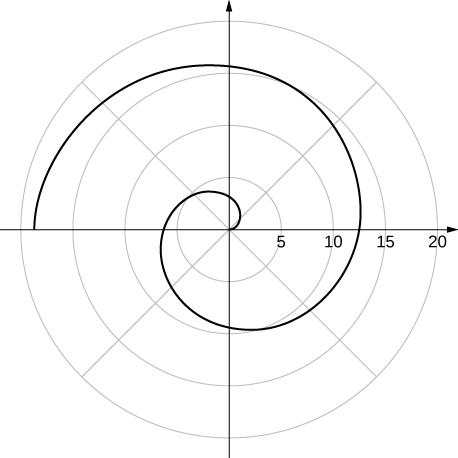
no symmetry
[T] The graph of
is called a strophoid. Use a graphing utility to sketch the graph, and, from the graph, determine the asymptote.
[T] Use a graphing utility and sketch the graph of
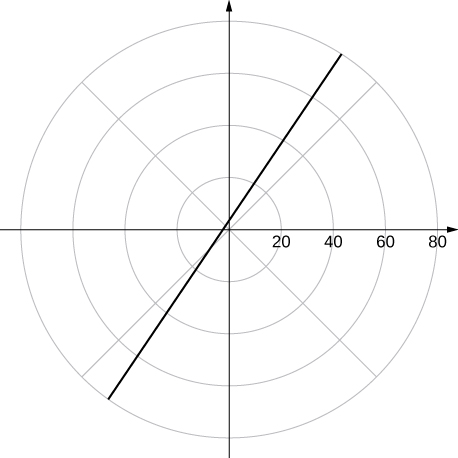
a line
[T] Use a graphing utility to graph
[T] Use technology to graph
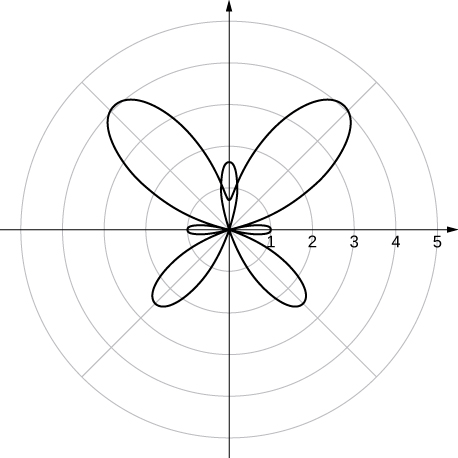
[T] Use technology to plot
(use the interval
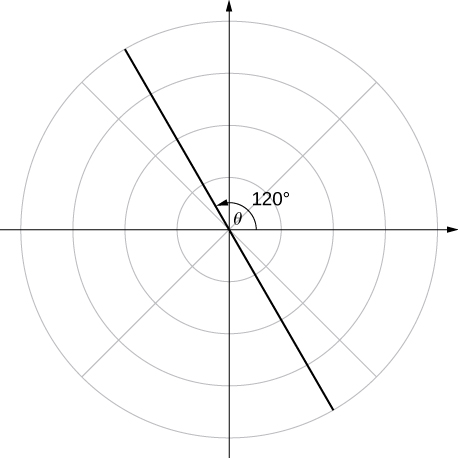
Without using technology, sketch the polar curve
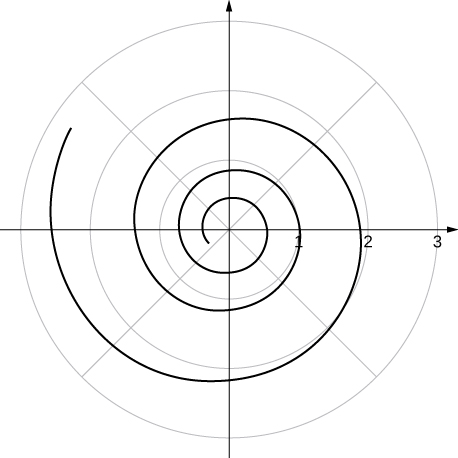
[T] Use a graphing utility to plot
for
[T] Use technology to plot
for
[T] There is a curve known as the “Black Hole.” Use technology to plot
for
[T] Use the results of the preceding two problems to explore the graphs of
and
for
Answers vary. One possibility is the spiral lines become closer together and the total number of spirals increases.
the angle formed by a line segment connecting the origin to a point in the polar coordinate system with the positive radial (x) axis, measured counterclockwise
or
or
If
then the graph is a cardioid
the radial coordinate, and
the angular coordinate
the coordinate in the polar coordinate system that measures the distance from a point in the plane to the pole
or
for a positive constant a

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: