Calculus of Parametric Curves

Now that we have introduced the concept of a parameterized curve, our next step is to learn how to work with this concept in the context of calculus. For example, if we know a parameterization of a given curve, is it possible to calculate the slope of a tangent line to the curve? How about the arc length of the curve? Or the area under the curve?

Another scenario: Suppose we would like to represent the location of a baseball after the ball leaves a pitcher’s hand. If the position of the baseball is represented by the plane curve (x(t),y(t)),

then we should be able to use calculus to find the speed of the ball at any given time. Furthermore, we should be able to calculate just how far that ball has traveled as a function of time.

Derivatives of Parametric Equations

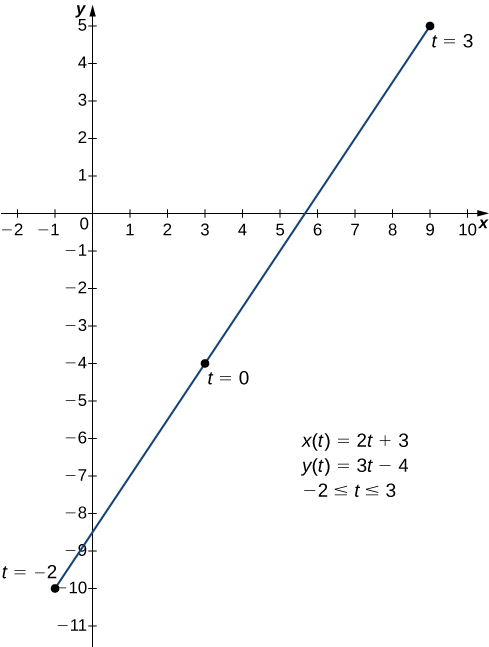
We start by asking how to calculate the slope of a line tangent to a parametric curve at a point. Consider the plane curve defined by the parametric equations

x(t)=2t+3,y(t)=3t−4,−2≤t≤3.

The graph of this curve appears in [link]. It is a line segment starting at (−1,−10)

and ending at (9,5).

A straight line from (−1, −10) to (9, 5). The point (−1, −10) is marked t = −2, the point (3, −4) is marked t = 0, and the point (9, 5) is marked t = 3. There are three equations marked: x(t) = 2t + 3, y(t) = 3t – 4, and −2 ≤ t ≤ 3

We can eliminate the parameter by first solving the equation x(t)=2t+3

for t:

x(t)=2t+3x−3=2tt=x−32.

Substituting this into y(t),

we obtain

y(t)=3t−4y=3(x−32)−4y=3x2−92−4y=3x2−172.

The slope of this line is given by dydx=32.

Next we calculate x′(t)

and y′(t).

This gives x′(t)=2

and y′(t)=3.

Notice that dydx=dy/dtdx/dt=32.

This is no coincidence, as outlined in the following theorem.

Derivative of Parametric Equations

Consider the plane curve defined by the parametric equations x=x(t)

and y=y(t).

Suppose that x′(t)

and y′(t)

exist, and assume that x′(t)≠0.

Then the derivative dydx

is given by

dydx=dy/dtdx/dt=y′(t)x′(t).

Proof

This theorem can be proven using the Chain Rule. In particular, assume that the parameter t can be eliminated, yielding a differentiable function y=F(x).

Then y(t)=F(x(t)).

Differentiating both sides of this equation using the Chain Rule yields

y′(t)=F′(x(t))x′(t),

so

F′(x(t))=y′(t)x′(t).

But F′(x(t))=dydx,

which proves the theorem.

□

[link] can be used to calculate derivatives of plane curves, as well as critical points. Recall that a critical point of a differentiable function y=f(x)

is any point x=x0

such that either f′(x0)=0

or f′(x0)

does not exist. [link] gives a formula for the slope of a tangent line to a curve defined parametrically regardless of whether the curve can be described by a function y=f(x)

or not.

Finding the Derivative of a Parametric Curve

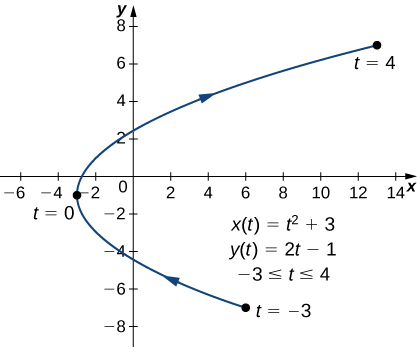
Calculate the derivative dydx

for each of the following parametrically defined plane curves, and locate any critical points on their respective graphs.

  1. x(t)=t2−3,y(t)=2t−1,−3≤t≤4
  2. x(t)=2t+1,y(t)=t3−3t+4,−2≤t≤5
  3. x(t)=5cost,y(t)=5sint,0≤t≤2π
  1. To apply [link], first calculate x′(t)

    and

    y′(t):
    x′(t)=2ty′(t)=2.

    Next substitute these into the equation:

    dydx=dy/dtdx/dtdydx=22tdydx=1t.

    This derivative is undefined when

    t=0.

    Calculating

    x(0)

    and

    y(0)

    gives

    x(0)=(0)2−3=−3

    and

    y(0)=2(0)−1=−1,

    which corresponds to the point

    (−3,−1)

    on the graph. The graph of this curve is a parabola opening to the right, and the point

    (−3,−1)

    is its vertex as shown.

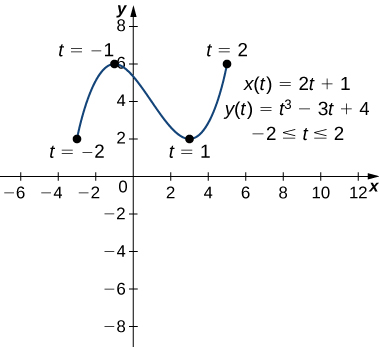
    A curved line going from (6, −7) through (−3, −1) to (13, 7) with arrow pointing in that order. The point (6, −7) is marked t = −3, the point (−3, −1) is marked t = 0, and the point (13, 7) is marked t = 4. On the graph there are also written three equations: x(t) = t2 − 3, y(t) = 2t − 1, and −3 ≤ t ≤ 4.

  2. To apply [link], first calculate x′(t)

    and

    y′(t):
    x′(t)=2y′(t)=3t2−3.

    Next substitute these into the equation:

    dydx=dy/dtdx/dtdydx=3t2−32.

    This derivative is zero when

    t=±1.

    When

    t=−1

    we have

    x(−1)=2(−1)+1=−1andy(−1)=(−1)3−3(−1)+4=−1+3+4=6,

    which corresponds to the point

    (−1,6)

    on the graph. When

    t=1

    we have

    x(1)=2(1)+1=3andy(1)=(1)3−3(1)+4=1−3+4=2,

    which corresponds to the point

    (3,2)

    on the graph. The point

    (3,2)

    is a relative minimum and the point

    (−1,6)

    is a relative maximum, as seen in the following graph.

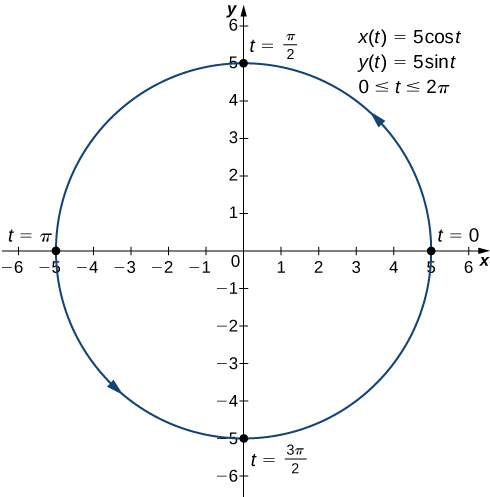
    A vaguely sinusoidal curve going from (−3, 2) through (−1, 6) and (3, 2) to (5, 6). The point (−3, 2) is marked t = −2, the point (−1, 6) is marked t = −1, the point (3, 2) is marked t = 1, and the point (5, 6) is marked t = 2. On the graph there are also written three equations: x(t) = 2t + 1, y(t) = t3 – 3t + 4, and −2 ≤ t ≤ 2.

  3. To apply [link], first calculate x′(t)

    and

    y′(t):
    x′(t)=−5sinty′(t)=5cost.

    Next substitute these into the equation:

    dydx=dy/dtdx/dtdydx=5cost−5sintdydx=−cott.

    This derivative is zero when

    cost=0

    and is undefined when

    sint=0.

    This gives

    t=0,π2,π,3π2,and2π

    as critical points for t. Substituting each of these into

    x(t)

    and

    y(t),

    we obtain

    t
    x(t)
    y(t)
         
    {: valign=”top”} ———-  
    0 5 0
    {: valign=”top”} π2  
    0 5
    {: valign=”top”} π
    −5 0
    {: valign=”top”} 3π2
    0 −5
    {: valign=”top”} 2π

    | 5 | 0 | {: valign=”top”}{: .unnumbered summary=”This table has three columns and six rows. The first row is a header row, and it reads from left to right t, x(t), and y(t). Below the header row, in the first column, the values read 0, π/2, π, 3π/2, and 2π. In the second column, the values read 5, 0, −5, 0, and 5. In the third column, the values read 0, 5, 0, −5, and 0.”}

    These points correspond to the sides, top, and bottom of the circle that is represented by the parametric equations ([link]). On the left and right edges of the circle, the derivative is undefined, and on the top and bottom, the derivative equals zero.

    A circle with radius 5 centered at the origin is graphed with arrow going counterclockwise. The point (5, 0) is marked t = 0, the point (0, 5) is marked t = π/2, the point (−5, 0) is marked t = π, and the point (0, −5) is marked t = 3π/2. On the graph there are also written three equations: x(t) = 5 cos(t), y(t) = 5 sin(t), and 0 ≤ t ≤ 2π.

Calculate the derivative dy/dx

for the plane curve defined by the equations

x(t)=t2−4t,y(t)=2t3−6t,−2≤t≤3

and locate any critical points on its graph.

x′(t)=2t−4

and y′(t)=6t2−6,

so dydx=6t2−62t−4=3t2−3t−2.

This expression is undefined when t=2

and equal to zero when t=±1.

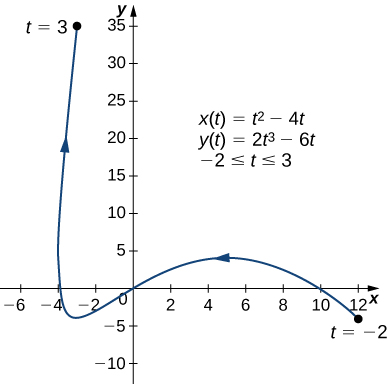
A curve going from (12, −4) through the origin and (−4, 0) to (−3, 36) with arrows in that order. The point (12, −4) is marked t = −2 and the point (−3, 36) is marked t = 3. On the graph there are also written three equations: x(t) = t2 – 4t, y(t) = 2t3 – 6t, and −2 ≤ t ≤ 3.

Hint

Calculate x′(t)

and y′(t)

and use [link].

Finding a Tangent Line

Find the equation of the tangent line to the curve defined by the equations

x(t)=t2−3,y(t)=2t−1,−3≤t≤4whent=2.

First find the slope of the tangent line using [link], which means calculating x′(t)

and y′(t):

x′(t)=2ty′(t)=2.

Next substitute these into the equation:

dydx=dy/dtdx/dtdydx=22tdydx=1t.

When t=2,

dydx=12,

so this is the slope of the tangent line. Calculating x(2)

and y(2)

gives

x(2)=(2)2−3=1andy(2)=2(2)−1=3,

which corresponds to the point (1,3)

on the graph ([link]). Now use the point-slope form of the equation of a line to find the equation of the tangent line:

y−y0=m(x−x0)y−3=12(x−1)y−3=12x−12y=12x+52.

A curved line going from (6, −7) through (−3, −1) to (13, 7) with arrow pointing in that order. The point (6, −7) is marked t = −3, the point (−3, −1) is marked t = 0, and the point (13, 7) is marked t = 4. On the graph there are also written three equations: x(t) = t2 − 3, y(t) = 2t − 1, and −3 ≤ t ≤ 4. At the point (1, 3), which is marked t = 2, there is a tangent line with equation y = x/2 + 5/2.

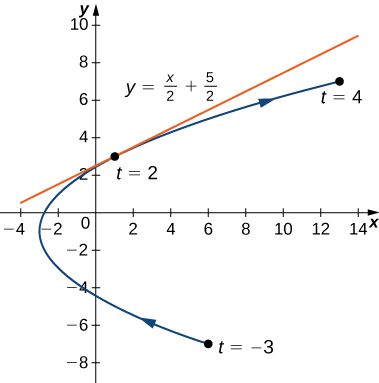
Find the equation of the tangent line to the curve defined by the equations

x(t)=t2−4t,y(t)=2t3−6t,−2≤t≤3whent=5.

The equation of the tangent line is y=24x+100.

Hint

Calculate x′(t)

and y′(t)

and use [link].

Second-Order Derivatives

Our next goal is to see how to take the second derivative of a function defined parametrically. The second derivative of a function y=f(x)

is defined to be the derivative of the first derivative; that is,

d2ydx2=ddx[dydx].

Since dydx=dy/dtdx/dt,

we can replace the y

on both sides of this equation with dydx.

This gives us

d2ydx2=ddx(dydx)=(d/dt)(dy/dx)dx/dt.

If we know dy/dx

as a function of t, then this formula is straightforward to apply.

Finding a Second Derivative

Calculate the second derivative d2y/dx2

for the plane curve defined by the parametric equations x(t)=t2−3,y(t)=2t−1,−3≤t≤4.

From [link] we know that dydx=22t=1t.

Using [link], we obtain

d2ydx2=(d/dt)(dy/dx)dx/dt=(d/dt)(1/t)2t=−t−22t=−12t3.

Calculate the second derivative d2y/dx2

for the plane curve defined by the equations

x(t)=t2−4t,y(t)=2t3−6t,−2≤t≤3

and locate any critical points on its graph.

d2ydx2=3t2−12t+32(t−2)3.

Critical points (5,4),(−3,−4),and(−4,6).

Hint

Start with the solution from the previous checkpoint, and use [link].

Integrals Involving Parametric Equations

Now that we have seen how to calculate the derivative of a plane curve, the next question is this: How do we find the area under a curve defined parametrically? Recall the cycloid defined by the equations x(t)=t−sint,y(t)=1−cost.

Suppose we want to find the area of the shaded region in the following graph.

A series of half circles drawn above the x axis with x intercepts being multiples of 2π. The half circle between 0 and 2π is highlighted. On the graph there are also written two equations: x(t) = t – sin(t) and y(t) = 1 – cos(t).

To derive a formula for the area under the curve defined by the functions

x=x(t),y=y(t),a≤t≤b,

we assume that x(t)

is differentiable and start with an equal partition of the interval a≤t≤b.

Suppose t0=a<t1<t2<⋯<tn=b

and consider the following graph.

A curved line is drawn in the first quadrant. Below it are a series of rectangles marked that begin at the x axis and reach up to the curved line; the rectangle’s height is determined by the location of the curved line at the leftmost point of the rectangle. These lines are noted as x(t0), x(t1), …, x(tn).

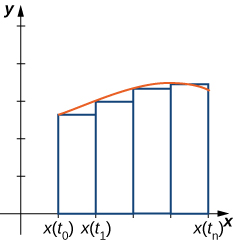
We use rectangles to approximate the area under the curve. The height of a typical rectangle in this parametrization is y(x(t–i))

for some value t–i

in the ith subinterval, and the width can be calculated as x(ti)−x(ti−1).

Thus the area of the ith rectangle is given by

Ai=y(x(t–i))(x(ti)−x(ti−1)).

Then a Riemann sum for the area is

An=∑i=1ny(x(t–i))(x(ti)−x(ti−1)).

Multiplying and dividing each area by ti−ti−1

gives

An=∑i=1ny(x(t–i))(x(ti)−x(ti−1)ti−ti−1)(ti−ti−1)=∑i=1ny(x(t–i))(x(ti)−x(ti−1)Δt)Δt.

Taking the limit as n

approaches infinity gives

A=limn→∞An=∫aby(t)x′(t)dt.

This leads to the following theorem.

Area under a Parametric Curve

Consider the non-self-intersecting plane curve defined by the parametric equations

x=x(t),y=y(t),a≤t≤b

and assume that x(t)

is differentiable. The area under this curve is given by

A=∫aby(t)x′(t)dt.
Finding the Area under a Parametric Curve

Find the area under the curve of the cycloid defined by the equations

x(t)=t−sint,y(t)=1−cost,0≤t≤2π.

Using [link], we have

A=∫aby(t)x′(t)dt=∫02π(1−cost)(1−cost)dt=∫02π(1−2cost+cos2t)dt=∫02π(1−2cost+1+cos2t2)dt=∫02π(32−2cost+cos2t2)dt=3t2−2sint+sin2t4\|02π=3π.

Find the area under the curve of the hypocycloid defined by the equations

x(t)=3cost+cos3t,y(t)=3sint−sin3t,0≤t≤π.
A=3π

(Note that the integral formula actually yields a negative answer. This is due to the fact that x(t)

is a decreasing function over the interval [0,2π];

that is, the curve is traced from right to left.)

Hint

Use [link], along with the identities sinαsinβ=12[cos(α−β)−cos(α+β)]

and sin2t=1−cos2t2.

Arc Length of a Parametric Curve

In addition to finding the area under a parametric curve, we sometimes need to find the arc length of a parametric curve. In the case of a line segment, arc length is the same as the distance between the endpoints. If a particle travels from point A to point B along a curve, then the distance that particle travels is the arc length. To develop a formula for arc length, we start with an approximation by line segments as shown in the following graph.

A curved line in the first quadrant with points marked for x = 1, 2, 3, 4, and 5. These points have values roughly 2.1, 2.7, 3, 2.7, and 2.1, respectively. The points for x = 1 and 5 are marked A and B, respectively.

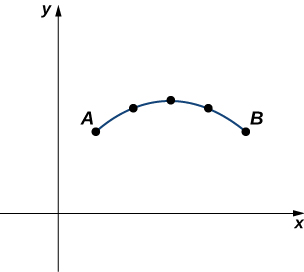
Given a plane curve defined by the functions x=x(t),y=y(t),a≤t≤b,

we start by partitioning the interval [a,b]

into n equal subintervals: t0=a<t1<t2<⋯<tn=b.

The width of each subinterval is given by Δt=(b−a)/n.

We can calculate the length of each line segment:

d1=(x(t1)−x(t0))2+(y(t1)−y(t0))2d2=(x(t2)−x(t1))2+(y(t2)−y(t1))2etc.

Then add these up. We let s denote the exact arc length and sn

denote the approximation by n line segments:

s≈∑k=1nsk=∑k=1n(x(tk)−x(tk−1))2+(y(tk)−y(tk−1))2.

If we assume that x(t)

and y(t)

are differentiable functions of t, then the Mean Value Theorem (Introduction to the Applications of Derivatives) applies, so in each subinterval [tk−1,tk]

there exist t^k

and t˜k

such that

x(tk)−x(tk−1)=x′(t^k)(tk−tk−1)=x′(t^k)Δty(tk)−y(tk−1)=y′(t˜k)(tk−tk−1)=y′(t˜k)Δt.

Therefore [link] becomes

s≈∑k=1nsk=∑k=1n(x′(t^k)Δt)2+(y′(t˜k)Δt)2=∑k=1n(x′(t^k))2(Δt)2+(y′(t˜k))2(Δt)2=(∑k=1n(x′(t^k))2+(y′(t˜k))2)Δt.

This is a Riemann sum that approximates the arc length over a partition of the interval [a,b].

If we further assume that the derivatives are continuous and let the number of points in the partition increase without bound, the approximation approaches the exact arc length. This gives

s=limn→∞∑k=1nsk=limn→∞(∑k=1n(x′(t^k))2+(y′(t˜k))2)Δt=∫ab(x′(t))2+(y′(t))2dt.

When taking the limit, the values of t^k

and t˜k

are both contained within the same ever-shrinking interval of width Δt,

so they must converge to the same value.

We can summarize this method in the following theorem.

Arc Length of a Parametric Curve

Consider the plane curve defined by the parametric equations

x=x(t),y=y(t),t1≤t≤t2

and assume that x(t)

and y(t)

are differentiable functions of t. Then the arc length of this curve is given by

s=∫t1t2(dxdt)2+(dydt)2dt.

At this point a side derivation leads to a previous formula for arc length. In particular, suppose the parameter can be eliminated, leading to a function y=F(x).

Then y(t)=F(x(t))

and the Chain Rule gives y′(t)=F′(x(t))x′(t).

Substituting this into [link] gives

s=∫t1t2(dxdt)2+(dydt)2dt=∫t1t2(dxdt)2+(F′(x)dxdt)2dt=∫t1t2(dxdt)2(1+(F′(x))2)dt=∫t1t2x′(t)1+(dydx)2dt.

Here we have assumed that x′(t)>0,

which is a reasonable assumption. The Chain Rule gives dx=x′(t)dt,

and letting a=x(t1)

and b=x(t2)

we obtain the formula

s=∫ab1+(dydx)2dx,

which is the formula for arc length obtained in the Introduction to the Applications of Integration.

Finding the Arc Length of a Parametric Curve

Find the arc length of the semicircle defined by the equations

x(t)=3cost,y(t)=3sint,0≤t≤π.

The values t=0

to t=π

trace out the red curve in [link]. To determine its length, use [link]:

s=∫t1t2(dxdt)2+(dydt)2dt=∫0π(−3sint)2+(3cost)2dt=∫0π9sin2t+9cos2tdt=∫0π9(sin2t+cos2t)dt=∫0π3dt=3t\|0π=3π.

Note that the formula for the arc length of a semicircle is πr

and the radius of this circle is 3. This is a great example of using calculus to derive a known formula of a geometric quantity.

A semicircle is drawn with radius 3. There is an arrow pointing counterclockwise. On the graph there are also written three equations: x(t) = 3 cos(t), y(t) = 3 sin(t), and 0 ≤ t ≤ π.

Find the arc length of the curve defined by the equations

x(t)=3t2,y(t)=2t3,1≤t≤3.
s=2(103/2−23/2)≈57.589
Hint

Use [link].

We now return to the problem posed at the beginning of the section about a baseball leaving a pitcher’s hand. Ignoring the effect of air resistance (unless it is a curve ball!), the ball travels a parabolic path. Assuming the pitcher’s hand is at the origin and the ball travels left to right in the direction of the positive x-axis, the parametric equations for this curve can be written as

x(t)=140t,y(t)=−16t2+2t

where t represents time. We first calculate the distance the ball travels as a function of time. This distance is represented by the arc length. We can modify the arc length formula slightly. First rewrite the functions x(t)

and y(t)

using v as an independent variable, so as to eliminate any confusion with the parameter t:

x(v)=140v,y(v)=−16v2+2v.

Then we write the arc length formula as follows:

s(t)=∫0t(dxdv)2+(dydv)2dv=∫0t1402+(−32v+2)2dv.

The variable v acts as a dummy variable that disappears after integration, leaving the arc length as a function of time t. To integrate this expression we can use a formula from Appendix A,

∫a2+u2du=u2a2+u2+a22ln\|u+a2+u2\|+C.

We set a=140

and u=−32v+2.

This gives du=−32dv,

so dv=−132du.

Therefore

∫1402+(−32v+2)2dv=−132∫a2+u2du=−132[(−32v+2)21402+(−32v+2)2+14022ln\|(−32v+2)+1402+(−32v+2)2\|]+C

and

s(t)=−132[(−32t+2)21402+(−32t+2)2+14022ln\|(−32t+2)+1402+(−32t+2)2\|]+132[1402+22+14022ln\|2+1402+22\|]=(t2−132)1024t2−128t+19604−12254ln\|(−32t+2)+1024t2−128t+19604\|+1960432+12254ln(2+19604).

This function represents the distance traveled by the ball as a function of time. To calculate the speed, take the derivative of this function with respect to t. While this may seem like a daunting task, it is possible to obtain the answer directly from the Fundamental Theorem of Calculus:

ddx∫axf(u)du=f(x).

Therefore

s′(t)=ddt[s(t)]=ddt[∫0t1402+(−32v+2)2dv]=1402+(−32t+2)2=1024t2−128t+19604=2256t2−32t+4901.

One third of a second after the ball leaves the pitcher’s hand, the distance it travels is equal to

s(13)=(1/32−132)1024(13)2−128(13)+19604−12254ln\|(−32(13)+2)+1024(13)2−128(13)+19604\|+1960432+12254ln(2+19604)≈46.69feet.

This value is just over three quarters of the way to home plate. The speed of the ball is

s′(13)=2256(13)2−16(13)+4901≈140.34ft/s.

This speed translates to approximately 95 mph—a major-league fastball.

Surface Area Generated by a Parametric Curve

Recall the problem of finding the surface area of a volume of revolution. In Curve Length and Surface Area, we derived a formula for finding the surface area of a volume generated by a function y=f(x)

from x=a

to x=b,

revolved around the x-axis:

S=2π∫abf(x)1+(f′(x))2dx.

We now consider a volume of revolution generated by revolving a parametrically defined curve x=x(t),y=y(t),a≤t≤b

around the x-axis as shown in the following figure.

A curve is drawn in the first quadrant with endpoints marked t = a and t = b. On this curve, there is a point marked (x(t), y(t)). There is a circle with an arrow drawn around the x axis that seems to indicate a rotation about the x axis, and there is a shape that accompanies that curve that seems to be what you would obtain if you rotated the curve about the x axis.

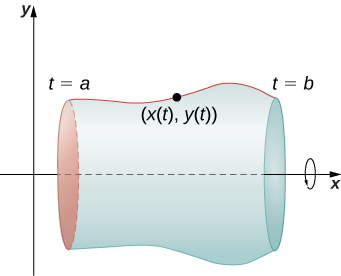
The analogous formula for a parametrically defined curve is

S=2π∫aby(t)(x′(t))2+(y′(t))2dt

provided that y(t)

is not negative on [a,b].

Finding Surface Area

Find the surface area of a sphere of radius r centered at the origin.

We start with the curve defined by the equations

x(t)=rcost,y(t)=rsint,0≤t≤π.

This generates an upper semicircle of radius r centered at the origin as shown in the following graph.

A semicircle is drawn with radius r. On the graph there are also written three equations: x(t) = r cos(t), y(t) = r sin(t), and 0 ≤ t ≤ π.

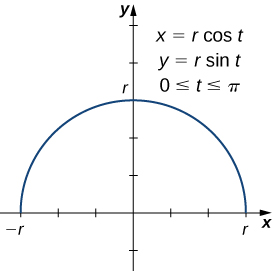
When this curve is revolved around the x-axis, it generates a sphere of radius r. To calculate the surface area of the sphere, we use [link]:

S=2π∫aby(t)(x′(t))2+(y′(t))2dt=2π∫0πrsint(−rsint)2+(rcost)2dt=2π∫0πrsintr2sin2t+r2cos2tdt=2π∫0πrsintr2(sin2t+cos2t)dt=2π∫0πr2sintdt=2πr2(−cost\|0π)=2πr2(−cosπ+cos0)=4πr2.

This is, in fact, the formula for the surface area of a sphere.

Find the surface area generated when the plane curve defined by the equations

x(t)=t3,y(t)=t2,0≤t≤1

is revolved around the x-axis.

A=π(49413+128)1215
Hint

Use [link]. When evaluating the integral, use a u-substitution.

Key Concepts

Key Equations

For the following exercises, each set of parametric equations represents a line. Without eliminating the parameter, find the slope of each line.

x=3+t,y=1−t
x=8+2t,y=1

0

x=4−3t,y=−2+6t
x=−5t+7,y=3t−1
−35

For the following exercises, determine the slope of the tangent line, then find the equation of the tangent line at the given value of the parameter.

x=3sint,y=3cost,t=π4
x=cost,y=8sint,t=π2
Slope=0; y=8.
x=2t,y=t3,t=−1
x=t+1t,y=t−1t,t=1

Slope is undefined; x=2.

x=t,y=2t,t=4

For the following exercises, find all points on the curve that have the given slope.

x=4cost,y=4sint,

slope = 0.5

t=arctan(−2); (45,−85).
x=2cost,y=8sint,slope=−1
x=t+1t,y=t−1t,slope=1

No points possible; undefined expression.

x=2+t,y=2−4t,slope=0

For the following exercises, write the equation of the tangent line in Cartesian coordinates for the given parameter t.

x=et,y=1−lnt2,t=1
y=−(2e)x+3
x=tlnt,y=sin2t,t=π4
x=et,y=(t−1)2,at(1,1)
y=2x−7

For x=sin(2t),y=2sint

where 0≤t<2π.

Find all values of t at which a horizontal tangent line exists.

For x=sin(2t),y=2sint

where 0≤t<2π.

Find all values of t at which a vertical tangent line exists.

π4,5π4,3π4,7π4

Find all points on the curve x=4cos(t),y=4sin(t)

that have the slope of 12.

Find dydx

for x=sin(t),y=cos(t).

dydx=−tan(t)

Find the equation of the tangent line to x=sin(t),y=cos(t)

at t=π4.

For the curve x=4t,y=3t−2,

find the slope and concavity of the curve at t=3.

dydx=34

and d2ydx2=0,

so the curve is neither concave up nor concave down at t=3.

Therefore the graph is linear and has a constant slope but no concavity.

For the parametric curve whose equation is x=4cosθ,y=4sinθ,

find the slope and concavity of the curve at θ=π4.

Find the slope and concavity for the curve whose equation is x=2+secθ,y=1+2tanθ

at θ=π6.

dydx=4,d2ydx2=−63;

the curve is concave down at θ=π6.

Find all points on the curve x=t+4,y=t3−3t

at which there are vertical and horizontal tangents.

Find all points on the curve x=secθ,y=tanθ

at which horizontal and vertical tangents exist.

No horizontal tangents. Vertical tangents at (1,0),(−1,0).

For the following exercises, find d2y/dx2.

x=t4−1,y=t−t2
x=sin(πt),y=cos(πt)
−sec3(πt)
x=e−t,y=te2t

For the following exercises, find points on the curve at which tangent line is horizontal or vertical.

x=t(t2−3),y=3(t2−3)

Horizontal (0,−9);

vertical (±2,−6).

x=3t1+t3,y=3t21+t3

For the following exercises, find dy/dx

at the value of the parameter.

x=cost,y=sint,t=3π4

1

x=t,y=2t+4,t=9
x=4cos(2πs),y=3sin(2πs),s=−14

0

For the following exercises, find d2y/dx2

at the given point without eliminating the parameter.

x=12t2,y=13t3,t=2
x=t,y=2t+4,t=1

4

Find t intervals on which the curve x=3t2,y=t3−t

is concave up as well as concave down.

Determine the concavity of the curve x=2t+lnt,y=2t−lnt.

Concave up on t>0.

Sketch and find the area under one arch of the cycloid x=r(θ−sinθ),y=r(1−cosθ).

Find the area bounded by the curve x=cost,y=et,0≤t≤π2

and the lines y=1

and x=0.

1

Find the area enclosed by the ellipse x=acosθ,y=bsinθ,0≤θ<2π.

Find the area of the region bounded by x=2sin2θ,y=2sin2θtanθ,

for 0≤θ≤π2.

3π2

For the following exercises, find the area of the regions bounded by the parametric curves and the indicated values of the parameter.

x=2cotθ,y=2sin2θ,0≤θ≤π

[T] x=2acost−acos(2t),y=2asint−asin(2t),0≤t<2π

6πa2

[T] x=asin(2t),y=bsin(t),0≤t<2π

(the “hourglass”)

[T] x=2acost−asin(2t),y=bsint,0≤t<2π

(the “teardrop”)

2πab

For the following exercises, find the arc length of the curve on the indicated interval of the parameter.

x=4t+3,y=3t−2,0≤t≤2
x=13t3,y=12t2,0≤t≤1
13(22−1)
x=cos(2t),y=sin(2t),0≤t≤π2
x=1+t2,y=(1+t)3,0≤t≤1
7.075
x=etcost,y=etsint,0≤t≤π2

(express answer as a decimal rounded to three places)

x=acos3θ,y=asin3θ

on the interval [0,2π)

(the hypocycloid)

6a

Find the length of one arch of the cycloid x=4(t−sint),y=4(1−cost).

Find the distance traveled by a particle with position (x,y)

as t varies in the given time interval: x=sin2t,y=cos2t,0≤t≤3π.

62

Find the length of one arch of the cycloid x=θ−sinθ,y=1−cosθ.

Show that the total length of the ellipse x=4sinθ,y=3cosθ

is L=16∫0π/21−e2sin2θdθ,

where e=ca

and c=a2−b2.

Find the length of the curve x=et−t,y=4et/2,−8≤t≤3.

For the following exercises, find the area of the surface obtained by rotating the given curve about the x-axis.

x=t3,y=t2,0≤t≤1
2π(24713+64)1215
x=acos3θ,y=asin3θ,0≤θ≤π2

[T] Use a CAS to find the area of the surface generated by rotating x=t+t3,y=t−1t2,1≤t≤2

about the x-axis. (Answer to three decimal places.)

59.101

Find the surface area obtained by rotating x=3t2,y=2t3,0≤t≤5

about the y-axis.

Find the area of the surface generated by revolving x=t2,y=2t,0≤t≤4

about the x-axis.

8π3(1717−1)

Find the surface area generated by revolving x=t2,y=2t2,0≤t≤1

about the y-axis.

Creative Commons License
This work is licensed under a Creative Commons Attribution 4.0 International License.

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1

Attribution: