Taylor and Maclaurin Series
- Describe the procedure for finding a Taylor polynomial of a given order for a function.
- Explain the meaning and significance of Taylor’s theorem with remainder.
- Estimate the remainder for a Taylor series approximation of a given function.
In the previous two sections we discussed how to find power series representations for certain types of functions––specifically, functions related to geometric series. Here we discuss power series representations for other types of functions. In particular, we address the following questions: Which functions can be represented by power series and how do we find such representations? If we can find a power series representation for a particular function
and the series converges on some interval, how do we prove that the series actually converges to
Overview of Taylor/Maclaurin Series
Consider a function
that has a power series representation at
Then the series has the form
What should the coefficients be? For now, we ignore issues of convergence, but instead focus on what the series should be, if one exists. We return to discuss convergence later in this section. If the series [link] is a representation for
at
we certainly want the series to equal
at
Evaluating the series at
we see that
Thus, the series equals
if the coefficient
In addition, we would like the first derivative of the power series to equal
at
Differentiating [link] term-by-term, we see that
Therefore, at
the derivative is
Therefore, the derivative of the series equals
if the coefficient
Continuing in this way, we look for coefficients cn such that all the derivatives of the power series [link] will agree with all the corresponding derivatives of
at
The second and third derivatives of [link] are given by
and
Therefore, at
the second and third derivatives
and
equal
and
respectively, if
and
More generally, we see that if
has a power series representation at
then the coefficients should be given by
That is, the series should be
This power series for
is known as the Taylor series for
at
If
then this series is known as the Maclaurin series for
Definition
If
has derivatives of all orders at
then the Taylor series for the function
at
is
The Taylor series for
at 0 is known as the Maclaurin series for
Later in this section, we will show examples of finding Taylor series and discuss conditions under which the Taylor series for a function will converge to that function. Here, we state an important result. Recall from [link] that power series representations are unique. Therefore, if a function
has a power series at
then it must be the Taylor series for
at
Uniqueness of Taylor Series
If a function
has a power series at a that converges to
on some open interval containing a, then that power series is the Taylor series for
at a.
The proof follows directly from [link].
To determine if a Taylor series converges, we need to look at its sequence of partial sums. These partial sums are finite polynomials, known as Taylor polynomials.
Taylor Polynomials
The nth partial sum of the Taylor series for a function
at
is known as the nth Taylor polynomial. For example, the 0th, 1st, 2nd, and 3rd partial sums of the Taylor series are given by
respectively. These partial sums are known as the 0th, 1st, 2nd, and 3rd Taylor polynomials of
at
respectively. If
then these polynomials are known as Maclaurin polynomials for
We now provide a formal definition of Taylor and Maclaurin polynomials for a function
Definition
If
has n derivatives at
then the nth Taylor polynomial for
at
is
The nth Taylor polynomial for
at 0 is known as the nth Maclaurin polynomial for
We now show how to use this definition to find several Taylor polynomials for
at
Finding Taylor Polynomials
Find the Taylor polynomials
and
for
at
Use a graphing utility to compare the graph of
with the graphs of
and
To find these Taylor polynomials, we need to evaluate
and its first three derivatives at
Therefore,
The graphs of
and the first three Taylor polynomials are shown in [link].
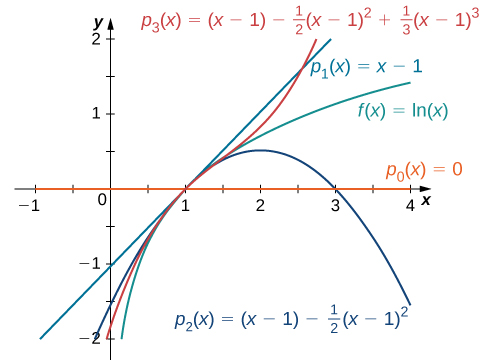
Find the Taylor polynomials
and
for
at
Hint
Find the first three derivatives of
and evaluate them at
We now show how to find Maclaurin polynomials for ex,
and
As stated above, Maclaurin polynomials are Taylor polynomials centered at zero.
Finding Maclaurin Polynomials
For each of the following functions, find formulas for the Maclaurin polynomials
and
Find a formula for the nth Maclaurin polynomial and write it using sigma notation. Use a graphing utilty to compare the graphs of
and
with
-
-
-
- Since
we know that
for all positive integers n. Therefore,
for all positive integers n. Therefore, we have
The function and the first three Maclaurin polynomials are shown in [link].
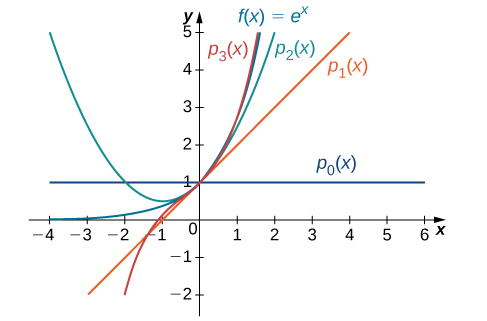
- For
the values of the function and its first four derivatives at
are given as follows:
Since the fourth derivative is
the pattern repeats. That is,
and
for
Thus, we have
and for
Graphs of the function and its Maclaurin polynomials are shown in [link].
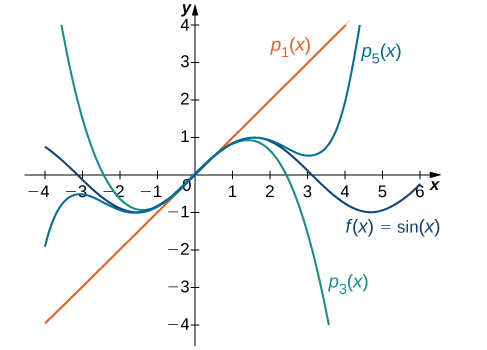
- For
the values of the function and its first four derivatives at
are given as follows:
Since the fourth derivative is
the pattern repeats. In other words,
and
for
Therefore,
and for
Graphs of the function and the Maclaurin polynomials appear in [link].
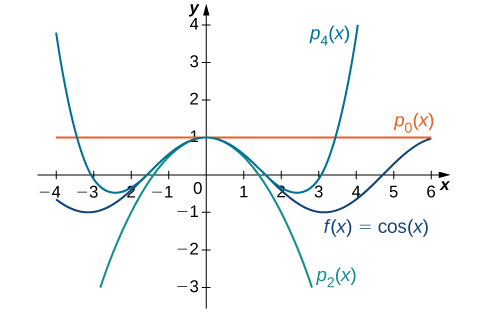
Find formulas for the Maclaurin polynomials
and
for
Find a formula for the nth Maclaurin polynomial. Write your anwer using sigma notation.
Hint
Evaluate the first four derivatives of
and look for a pattern.
Taylor’s Theorem with Remainder
Recall that the nth Taylor polynomial for a function
at a is the nth partial sum of the Taylor series for
at a. Therefore, to determine if the Taylor series converges, we need to determine whether the sequence of Taylor polynomials
converges. However, not only do we want to know if the sequence of Taylor polynomials converges, we want to know if it converges to
To answer this question, we define the remainder
as
For the sequence of Taylor polynomials to converge to
we need the remainder Rn to converge to zero. To determine if Rn converges to zero, we introduce Taylor’s theorem with remainder. Not only is this theorem useful in proving that a Taylor series converges to its related function, but it will also allow us to quantify how well the nth Taylor polynomial approximates the function.
Here we look for a bound on
Consider the simplest case:
Let p0 be the 0th Taylor polynomial at a for a function
The remainder R0 satisfies
If
is differentiable on an interval I containing a and x, then by the Mean Value Theorem there exists a real number c between a and x such that
Therefore,
Using the Mean Value Theorem in a similar argument, we can show that if
is n times differentiable on an interval I containing a and x, then the nth remainder Rn satisfies
for some real number c between a and x. It is important to note that the value c in the numerator above is not the center a, but rather an unknown value c between a and x. This formula allows us to get a bound on the remainder Rn. If we happen to know that
is bounded by some real number M on this interval I, then
for all x in the interval I.
We now state Taylor’s theorem, which provides the formal relationship between a function
and its nth degree Taylor polynomial
This theorem allows us to bound the error when using a Taylor polynomial to approximate a function value, and will be important in proving that a Taylor series for
converges to
Taylor’s Theorem with Remainder
Let
be a function that can be differentiated
times on an interval I containing the real number a. Let pn be the nth Taylor polynomial of
at a and let
be the nth remainder. Then for each x in the interval I, there exists a real number c between a and x such that
If there exists a real number M such that
for all
then
for all x in I.
Proof
Fix a point
and introduce the function g such that
We claim that g satisfies the criteria of Rolle’s theorem. Since g is a polynomial function (in t), it is a differentiable function. Also, g is zero at
and
because
Therefore, g satisfies Rolle’s theorem, and consequently, there exists c between a and x such that
We now calculate
Using the product rule, we note that
Consequently,
Notice that there is a telescoping effect. Therefore,
By Rolle’s theorem, we conclude that there exists a number c between a and x such that
Since
we conclude that
Adding the first term on the left-hand side to both sides of the equation and dividing both sides of the equation by
we conclude that
as desired. From this fact, it follows that if there exists M such that
for all x in I, then
□
Not only does Taylor’s theorem allow us to prove that a Taylor series converges to a function, but it also allows us to estimate the accuracy of Taylor polynomials in approximating function values. We begin by looking at linear and quadratic approximations of
at
and determine how accurate these approximations are at estimating
Using Linear and Quadratic Approximations to Estimate Function Values
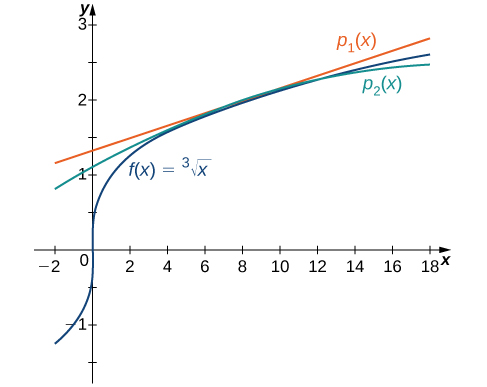
Consider the function
- Find the first and second Taylor polynomials for
at
Use a graphing utility to compare these polynomials with
near
- Use these two polynomials to estimate
- Use Taylor’s theorem to bound the error.
- For
the values of the function and its first two derivatives at
are as follows:
Thus, the first and second Taylor polynomials at
are given by
The function and the Taylor polynomials are shown in [link].
- Using the first Taylor polynomial at
we can estimate
Using the second Taylor polynomial at
we obtain
- By [link], there exists a c in the interval
such that the remainder when approximating
by the first Taylor polynomial satisfies
We do not know the exact value of c, so we find an upper bound on
by determining the maximum value of
on the interval
Since
the largest value for
on that interval occurs at
Using the fact that
we obtain
Similarly, to estimate
we use the fact that
Since
the maximum value of
on the interval
is
Therefore, we have
Find the first and second Taylor polynomials for
at
Use these polynomials to estimate
Use Taylor’s theorem to bound the error.
Hint
Evaluate
and
Approximating sin *x* Using Maclaurin Polynomials
From [link]b., the Maclaurin polynomials for
are given by
for
- Use the fifth Maclaurin polynomial for
to approximate
and bound the error.
- For what values of x does the fifth Maclaurin polynomial approximate
to within 0.0001?
- The fifth Maclaurin polynomial is
Using this polynomial, we can estimate as follows:
To estimate the error, use the fact that the sixth Maclaurin polynomial is
and calculate a bound on
By [link], the remainder is
for some c between 0 and
Using the fact that
for all x, we find that the magnitude of the error is at most
- We need to find the values of x such that
Solving this inequality for x, we have that the fifth Maclaurin polynomial gives an estimate to within 0.0001 as long as
Use the fourth Maclaurin polynomial for
to approximate
Hint
The fourth Maclaurin polynomial is
Now that we are able to bound the remainder
we can use this bound to prove that a Taylor series for
at a converges to
Representing Functions with Taylor and Maclaurin Series
We now discuss issues of convergence for Taylor series. We begin by showing how to find a Taylor series for a function, and how to find its interval of convergence.
Finding a Taylor Series
Find the Taylor series for
at
Determine the interval of convergence.
For
the values of the function and its first four derivatives at
are
That is, we have
for all
Therefore, the Taylor series for
at
is given by
To find the interval of convergence, we use the ratio test. We find that
Thus, the series converges if
That is, the series converges for
Next, we need to check the endpoints. At
we see that
diverges by the divergence test. Similarly, at
diverges. Therefore, the interval of convergence is
Find the Taylor series for
at
and determine its interval of convergence.
The interval of convergence is
We know that the Taylor series found in this example converges on the interval
but how do we know it actually converges to
We consider this question in more generality in a moment, but for this example, we can answer this question by writing
That is,
can be represented by the geometric series
Since this is a geometric series, it converges to
as long as
Therefore, the Taylor series found in [link] does converge to
on
We now consider the more general question: if a Taylor series for a function
converges on some interval, how can we determine if it actually converges to
To answer this question, recall that a series converges to a particular value if and only if its sequence of partial sums converges to that value. Given a Taylor series for
at a, the nth partial sum is given by the nth Taylor polynomial pn. Therefore, to determine if the Taylor series converges to
we need to determine whether
Since the remainder
the Taylor series converges to
if and only if
We now state this theorem formally.
Convergence of Taylor Series
Suppose that
has derivatives of all orders on an interval I containing a. Then the Taylor series
converges to
for all x in I if and only if
for all x in I.
With this theorem, we can prove that a Taylor series for
at a converges to
if we can prove that the remainder
To prove that
we typically use the bound
from Taylor’s theorem with remainder.
In the next example, we find the Maclaurin series for ex and
and show that these series converge to the corresponding functions for all real numbers by proving that the remainders
for all real numbers x.
Finding Maclaurin Series
For each of the following functions, find the Maclaurin series and its interval of convergence. Use [link] to prove that the Maclaurin series for
converges to
on that interval.
- ex
-
- Using the nth Maclaurin polynomial for ex found in [link]a., we find that the Maclaurin series for ex is given by
To determine the interval of convergence, we use the ratio test. Since
we have
for all x. Therefore, the series converges absolutely for all x, and thus, the interval of convergence is
To show that the series converges to ex for all x, we use the fact that
for all
and ex is an increasing function on
Therefore, for any real number b, the maximum value of ex for all
is eb. Thus,
Since we just showed that
converges for all x, by the divergence test, we know that
for any real number x. By combining this fact with the squeeze theorem, the result is
- Using the nth Maclaurin polynomial for
found in [link]b., we find that the Maclaurin series for
is given by
In order to apply the ratio test, consider
Since
for all x, we obtain the interval of convergence as
To show that the Maclaurin series converges to
look at
For each x there exists a real number c between 0 and x such that
Since
for all integers n and all real numbers c, we have
for all real numbers x. Using the same idea as in part a., the result is
for all x, and therefore, the Maclaurin series for
converges to
for all real x.
Find the Maclaurin series for
Use the ratio test to show that the interval of convergence is
Show that the Maclaurin series converges to
for all real numbers x.
By the ratio test, the interval of convergence is
Since
the series converges to
for all real x.
Hint
Use the Maclaurin polynomials for
Proving that *e* is Irrational
In this project, we use the Maclaurin polynomials for ex to prove that e is irrational. The proof relies on supposing that e is rational and arriving at a contradiction. Therefore, in the following steps, we suppose
for some integers r and s where
- Write the Maclaurin polynomials
for ex. Evaluate
to estimate e.
- Let
denote the remainder when using
to estimate ex. Therefore,
and
Assuming that
for integers r and s, evaluate
- Using the results from part 2, show that for each remainder
we can find an integer k such that
is an integer for
- Write down the formula for the nth Maclaurin polynomial
for ex and the corresponding remainder
Show that
is an integer.
- Use Taylor’s theorem to write down an explicit formula for
Conclude that
and therefore,
- Use Taylor’s theorem to find an estimate on
Use this estimate combined with the result from part 5 to show that
Conclude that if n is large enough, then
Therefore,
is an integer with magnitude less than 1. Thus,
But from part 5, we know that
We have arrived at a contradiction, and consequently, the original supposition that e is rational must be false.
Key Concepts
- Taylor polynomials are used to approximate functions near a value
Maclaurin polynomials are Taylor polynomials at
- The nth degree Taylor polynomials for a function
are the partial sums of the Taylor series for
- If a function
has a power series representation at
then it is given by its Taylor series at
- A Taylor series for
converges to
if and only if
where
- The Taylor series for ex,
and
converge to the respective functions for all real x.
Key Equations
In the following exercises, find the Taylor polynomials of degree two approximating the given function centered at the given point.
In the following exercises, verify that the given choice of n in the remainder estimate
where M is the maximum value of
on the interval between a and the indicated point, yields
Find the value of the Taylor polynomial pn of
at the indicated point.
when
so the remainder estimate applies to the linear approximation
which gives
while
Using the estimate
we can use the Taylor expansion of order 9 to estimate ex at
as
whereas
Since
One has
whereas
Integrate the approximation
evaluated at πt to approximate
Integrate the approximation
evaluated at −x2 to approximate
whereas
In the following exercises, find the smallest value of n such that the remainder estimate
where M is the maximum value of
on the interval between a and the indicated point, yields
on the indicated interval.
on
Since
is
or
we have
Since
we seek the smallest n such that
The smallest such value is
The remainder estimate is
Since
one has
Since
one seeks the smallest n such that
The smallest such value is
The remainder estimate is
In the following exercises, the maximum of the right-hand side of the remainder estimate
on
occurs at a or
Estimate the maximum value of R such that
on
by plotting this maximum as a function of R.
[T] ex approximated by
[T]
approximated by x,
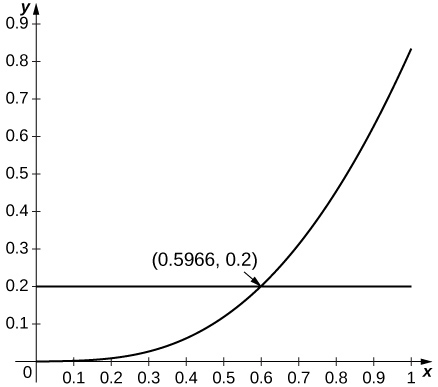
Since
is increasing for small x and since
the estimate applies whenever
which applies up to
[T]
approximated by
[T]
approximated by
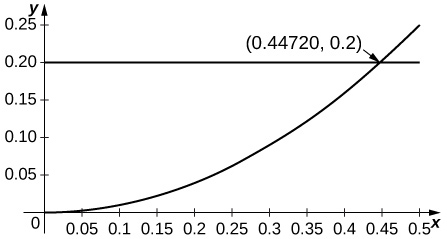
Since the second derivative of
is
and since
is decreasing away from
the estimate applies when
or
In the following exercises, find the Taylor series of the given function centered at the indicated point.
Values of derivatives are the same as for
so
so
which is also
The derivatives are
so
at
(Hint: Differentiate
at
(Note:
is the Taylor series of
In the following exercises, compute the Taylor series of each function around
[T] In the following exercises, identify the value of x such that the given series
is the value of the Maclaurin series of
at
Approximate the value of
using
The following exercises make use of the functions
and
on
[T] Plot
on
Compare the maximum difference with the square of the Taylor remainder estimate for
[T] Plot
on
Compare the maximum difference with the square of the Taylor remainder estimate for
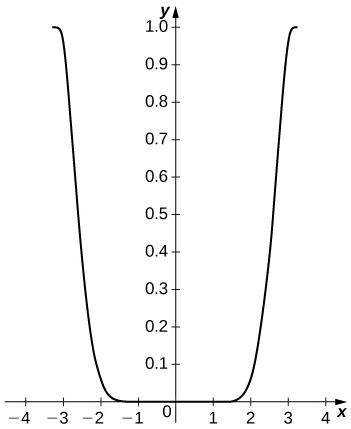
The difference is small on the interior of the interval but approaches
near the endpoints. The remainder estimate is
[T] Plot
on
[T] Compare
on
to
Compare this with the Taylor remainder estimate for the approximation of
by
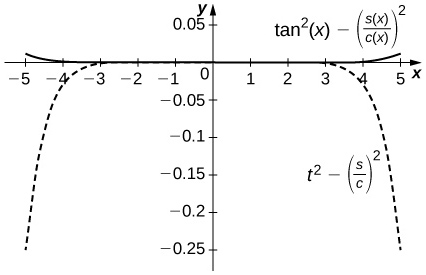
The difference is on the order of
on
while the Taylor approximation error is around
near
The top curve is a plot of
and the lower dashed plot shows
[T] Plot
where
on
Compare the maximum error with the Taylor remainder estimate.
(Taylor approximations and root finding.) Recall that Newton’s method
approximates solutions of
near the input
- If
and
are inverse functions, explain why a solution of
is the value
- Let
be the
degree Maclaurin polynomial of
Use Newton’s method to approximate solutions of
for
- Explain why the approximate roots of
are approximate values of
a. Answers will vary. b. The following are the
values after
iterations of Newton’s method to approximation a root of
for
for
for
(Note:
c. Answers will vary.
In the following exercises, use the fact that if
converges in an interval containing
then
to evaluate each limit using Taylor series.
Glossary
- Maclaurin polynomial
- a Taylor polynomial centered at 0; the nth Taylor polynomial for
at 0 is the nth Maclaurin polynomial for
- Maclaurin series
- a Taylor series for a function
at
is known as a Maclaurin series for
- Taylor polynomials
- the nth Taylor polynomial for
at
is
- Taylor series
- a power series at a that converges to a function
on some open interval containing a
- Taylor’s theorem with remainder
- for a function
and the nth Taylor polynomial for
at
the remainder
satisfies
for some c between x and a; if there exists an interval I containing a and a real number M such that
for all x in I, then

This work is licensed under a Creative Commons Attribution 4.0 International License.
You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution:









