Properties of Power Series

In the preceding section on power series and functions we showed how to represent certain functions using power series. In this section we discuss how power series can be combined, differentiated, or integrated to create new power series. This capability is particularly useful for a couple of reasons. First, it allows us to find power series representations for certain elementary functions, by writing those functions in terms of functions with known power series. For example, given the power series representation for

f (x) = \frac{1}{1 - x},

we can find a power series representation for

f^{'} (x) = \frac{1}{{(1 - x)}^{2}} .

Second, being able to create power series allows us to define new functions that cannot be written in terms of elementary functions. This capability is particularly useful for solving differential equations for which there is no solution in terms of elementary functions.

Combining Power Series

If we have two power series with the same interval of convergence, we can add or subtract the two series to create a new power series, also with the same interval of convergence. Similarly, we can multiply a power series by a power of x or evaluate a power series at

x^{m}

for a positive integer m to create a new power series. Being able to do this allows us to find power series representations for certain functions by using power series representations of other functions. For example, since we know the power series representation for

f (x) = \frac{1}{1 - x},

In [link] we state results regarding addition or subtraction of power series, composition of a power series, and multiplication of a power series by a power of the variable. For simplicity, we state the theorem for power series centered at

x = 0 .

Proof

We prove i. in the case of the series

\sum_{n = 0}^{\infty} (c_{n} x^{n} + d_{n} x^{n}) .

converge to the functions f and g, respectively, on the interval I. Let x be a point in I and let

S_{N} (x)

Furthermore, the Nth partial sum of

\sum_{n = 0}^{\infty} (c_{n} x^{n} + d_{n} x^{n})

We examine products of power series in a later theorem. First, we show several applications of [link] and how to find the interval of convergence of a power series given the interval of convergence of a related power series.

In the next example, we show how to use [link] and the power series for a function f to construct power series for functions related to f. Specifically, we consider functions related to the function

f (x) = \frac{1}{1 - x}

In [link], we showed how to find power series for certain functions. In [link] we show how to do the opposite: given a power series, determine which function it represents.

Recall the questions posed in the chapter opener about which is the better way of receiving payouts from lottery winnings. We now revisit those questions and show how to use series to compare values of payments over time with a lump sum payment today. We will compute how much future payments are worth in terms of today’s dollars, assuming we have the ability to invest winnings and earn interest. The value of future payments in terms of today’s dollars is known as the present value of those payments.

Multiplication of Power Series

We can also create new power series by multiplying power series. Being able to multiply two power series provides another way of finding power series representations for functions.

The way we multiply them is similar to how we multiply polynomials. For example, suppose we want to multiply

In [link], we state the main result regarding multiplying power series, showing that if

\sum_{n = 0}^{\infty} c_{n} x^{n}

converge on a common interval I, then we can multiply the series in this way, and the resulting series also converges on the interval I.

We omit the proof of this theorem, as it is beyond the level of this text and is typically covered in a more advanced course. We now provide an example of this theorem by finding the power series representation for

Differentiating and Integrating Power Series

Consider a power series

\sum_{n = 0}^{\infty} c_{n} x^{n} = c_{0} + c_{1} x + c_{2} x^{2} + ⋯

be the function defined by this series. Here we address two questions about

f .

We know that, for a polynomial with a finite number of terms, we can evaluate the derivative by differentiating each term separately. Similarly, we can evaluate the indefinite integral by integrating each term separately. Here we show that we can do the same thing for convergent power series. That is, if

Evaluating the derivative and indefinite integral in this way is called term-by-term differentiation of a power series and term-by-term integration of a power series, respectively. The ability to differentiate and integrate power series term-by-term also allows us to use known power series representations to find power series representations for other functions. For example, given the power series for

f (x) = \frac{1}{1 - x},

we can differentiate term-by-term to find the power series for

f^{'} (x) = \frac{1}{{(1 - x)}^{2}} .

we can integrate term-by-term to find the power series for

G (x) = ln (1 + x),

an antiderivative of g. We show how to do this in [link] and [link]. First, we state [link], which provides the main result regarding differentiation and integration of power series.

The proof of this result is beyond the scope of the text and is omitted. Note that although [link] guarantees the same radius of convergence when a power series is differentiated or integrated term-by-term, it says nothing about what happens at the endpoints. It is possible that the differentiated and integrated power series have different behavior at the endpoints than does the original series. We see this behavior in the next examples.

Integrating Power Series

For each of the following functions f, find a power series representation for f by integrating the power series for $f^{'}$

and find its interval of convergence.

$f (x) = ln (1 + x)$
$f (x) = {tan}^{−1} x$

For $f (x) = ln (1 + x),$
the derivative is
$f^{'} (x) = \frac{1}{1 + x} .$
We know that

$\begin{matrix} \frac{1}{1 + x} & = \frac{1}{1 - (− x)} \\ = \sum_{n = 0}^{\infty} {(− x)}^{n} \\ = 1 - x + x^{2} - x^{3} + ⋯ \end{matrix}$

for
$\| x \| < 1 .$
To find a power series for
$f (x) = ln (1 + x),$
we integrate the series term-by-term.

$\begin{matrix} \int f^{'} (x) d x & = \int (1 - x + x^{2} - x^{3} + ⋯) d x \\ = C + x - \frac{x^{2}}{2} + \frac{x^{3}}{3} - \frac{x^{4}}{4} + ⋯ \end{matrix}$

Since
$f (x) = ln (1 + x)$
is an antiderivative of
$\frac{1}{1 + x},$
it remains to solve for the constant C. Since
$ln (1 + 0) = 0,$
we have
$C = 0 .$
Therefore, a power series representation for
$f (x) = ln (1 + x)$
is

$\begin{matrix} ln (1 + x) & = x - \frac{x^{2}}{2} + \frac{x^{3}}{3} - \frac{x^{4}}{4} + ⋯ \\ = \sum_{n = 1}^{\infty} {(−1)}^{n + 1} \frac{x^{n}}{n} \end{matrix}$

for
$\| x \| < 1 .$
[link] does not guarantee anything about the behavior of this power series at the endpoints. However, checking the endpoints, we find that at
$x = 1$
the series is the alternating harmonic series, which converges. Also, at
$x = −1,$
the series is the harmonic series, which diverges. It is important to note that, even though this series converges at
$x = 1,$
[link] does not guarantee that the series actually converges to
$ln (2) .$
In fact, the series does converge to
$ln (2),$
but showing this fact requires more advanced techniques. (Abel’s theorem, covered in more advanced texts, deals with this more technical point.) The interval of convergence is
$(−1, 1] .$
The derivative of $f (x) = {tan}^{−1} x$
is
$f^{'} (x) = \frac{1}{1 + x^{2}} .$
We know that

$\begin{matrix} \frac{1}{1 + x^{2}} & = \frac{1}{1 - (− x^{2})} \\ = \sum_{n = 0}^{\infty} {(− x^{2})}^{n} \\ = 1 - x^{2} + x^{4} - x^{6} + ⋯ \end{matrix}$

for
$\| x \| < 1 .$
To find a power series for
$f (x) = {tan}^{−1} x,$
we integrate this series term-by-term.

$\begin{matrix} \int f^{'} (x) d x & = \int (1 - x^{2} + x^{4} - x^{6} + ⋯) d x \\ = C + x - \frac{x^{3}}{3} + \frac{x^{5}}{5} - \frac{x^{7}}{7} + ⋯ \end{matrix}$

Since
${tan}^{−1} (0) = 0,$
we have
$C = 0 .$
Therefore, a power series representation for
$f (x) = {tan}^{−1} x$
is

$\begin{matrix} {tan}^{−1} x & = x - \frac{x^{3}}{3} + \frac{x^{5}}{5} - \frac{x^{7}}{7} + ⋯ \\ = \sum_{n = 0}^{\infty} {(−1)}^{n} \frac{x^{2 n + 1}}{2 n + 1} \end{matrix}$

for
$\| x \| < 1 .$
Again, [link] does not guarantee anything about the convergence of this series at the endpoints. However, checking the endpoints and using the alternating series test, we find that the series converges at
$x = 1$
and
$x = −1 .$
As discussed in part a., using Abel’s theorem, it can be shown that the series actually converges to
${tan}^{−1} (1)$
and
${tan}^{−1} (−1)$
at
$x = 1$
and
$x = −1,$
respectively. Thus, the interval of convergence is
$[−1, 1] .$

Up to this point, we have shown several techniques for finding power series representations for functions. However, how do we know that these power series are unique? That is, given a function f and a power series for f at a, is it possible that there is a different power series for f at a that we could have found if we had used a different technique? The answer to this question is no. This fact should not seem surprising if we think of power series as polynomials with an infinite number of terms. Intuitively, if

for all values x in some open interval I about zero, then the coefficients c_n should equal d_n for

n \geq 0 .

Proof

In this section we have shown how to find power series representations for certain functions using various algebraic operations, differentiation, or integration. At this point, however, we are still limited as to the functions for which we can find power series representations. Next, we show how to find power series representations for many more functions by introducing Taylor series.

Key Concepts

If $f (x) = \sum_{n = 0}^{\infty} \frac{x^{n}}{n!}$

and $g (x) = \sum_{n = 0}^{\infty} {(−1)}^{n} \frac{x^{n}}{n!},$

find the power series of $\frac{1}{2} (f (x) + g (x))$

and of $\frac{1}{2} (f (x) - g (x)) .$

\frac{1}{2} (f (x) + g (x)) = \sum_{n = 0}^{\infty} \frac{x^{2 n}}{(2 n)!}

and $\frac{1}{2} (f (x) - g (x)) = \sum_{n = 0}^{\infty} \frac{x^{2 n + 1}}{(2 n + 1)!} .$

If $C (x) = \sum_{n = 0}^{\infty} \frac{x^{2 n}}{(2 n)!}$

and $S (x) = \sum_{n = 0}^{\infty} \frac{x^{2 n + 1}}{(2 n + 1)!},$

find the power series of $C (x) + S (x)$

and of $C (x) - S (x) .$

In the following exercises, use partial fractions to find the power series of each function.

\frac{4}{(x - 3) (x + 1)}

\frac{4}{(x - 3) (x + 1)} = \frac{1}{x - 3} - \frac{1}{x + 1} = - \frac{1}{3 (1 - \frac{x}{3})} - \frac{1}{1 - (− x)} = - \frac{1}{3} \sum_{n = 0}^{\infty} {(\frac{x}{3})}^{n} - \sum_{n = 0}^{\infty} {(−1)}^{n} x^{n} = \sum_{n = 0}^{\infty} ({(−1)}^{n + 1} - \frac{1}{3^{n + 1}}) x^{n}

\frac{3}{(x + 2) (x - 1)}

\frac{5}{(x^{2} + 4) (x^{2} - 1)}

\frac{5}{(x^{2} + 4) (x^{2} - 1)} = \frac{1}{x^{2} - 1} - \frac{1}{4} \frac{1}{1 + {(\frac{x}{2})}^{2}} = − \sum_{n = 0}^{\infty} x^{2 n} - \frac{1}{4} \sum_{n = 0}^{\infty} {(−1)}^{n} {(\frac{x}{2})}^{n} = \sum_{n = 0}^{\infty} ((−1) + {(−1)}^{n + 1} \frac{1}{2^{n + 2}}) x^{2 n}

\frac{30}{(x^{2} + 1) (x^{2} - 9)}

In the following exercises, express each series as a rational function.

\sum_{n = 1}^{\infty} \frac{1}{x^{n}}

\frac{1}{x} \sum_{n = 0}^{\infty} \frac{1}{x^{n}} = \frac{1}{x} \frac{1}{1 - \frac{1}{x}} = \frac{1}{x - 1}

\sum_{n = 1}^{\infty} \frac{1}{x^{2 n}}

\sum_{n = 1}^{\infty} \frac{1}{{(x - 3)}^{2 n - 1}}

\frac{1}{x - 3} \frac{1}{1 - \frac{1}{{(x - 3)}^{2}}} = \frac{x - 3}{{(x - 3)}^{2} - 1}

\sum_{n = 1}^{\infty} (\frac{1}{{(x - 3)}^{2 n - 1}} - \frac{1}{{(x - 2)}^{2 n - 1}})

The following exercises explore applications of annuities.

Calculate the present values P of an annuity in which $10,000 is to be paid out annually for a period of 20 years, assuming interest rates of $r = 0.03, r = 0.05,$

and $r = 0.07 .$

P = P_{1} + ⋯ + P_{20}

where $P_{k} = 10,000 \frac{1}{{(1 + r)}^{k}} .$

Then $P = 10,000 \sum_{k = 1}^{20} \frac{1}{{(1 + r)}^{k}} = 10,000 \frac{1 - {(1 + r)}^{−20}}{r} .$

When $r = 0.03, P \approx 10,000 \times 14.8775 = 148,775 .$

When $r = 0.05, P \approx 10,000 \times 12.4622 = 124,622 .$

When $r = 0.07, P \approx 105,940 .$

Calculate the present values P of annuities in which $9,000 is to be paid out annually perpetually, assuming interest rates of $r = 0.03, r = 0.05$

and $r = 0.07 .$

Calculate the annual payouts C to be given for 20 years on annuities having present value $100,000 assuming respective interest rates of $r = 0.03, r = 0.05,$

and $r = 0.07 .$

In general, $P = \frac{C (1 - {(1 + r)}^{− N})}{r}$

for N years of payouts, or $C = \frac{P r}{1 - {(1 + r)}^{− N}} .$

For $N = 20$

and $P = 100,000,$

one has $C = 6721.57$

when $r = 0.03; C = 8024.26$

when $r = 0.05;$

and $C \approx 9439.29$

when $r = 0.07 .$

Calculate the annual payouts C to be given perpetually on annuities having present value $100,000 assuming respective interest rates of $r = 0.03, r = 0.05,$

and $r = 0.07 .$

Suppose that an annuity has a present value $P = 1 million dollars .$

What interest rate r would allow for perpetual annual payouts of $50,000?

In general, $P = \frac{C}{r} .$

Thus, $r = \frac{C}{P} = 5 \times \frac{10^{4}}{10^{6}} = 0.05 .$

Suppose that an annuity has a present value $P = 10 million dollars .$

What interest rate r would allow for perpetual annual payouts of $100,000?

In the following exercises, express the sum of each power series in terms of geometric series, and then express the sum as a rational function.

x + x^{2} - x^{3} + x^{4} + x^{5} - x^{6} + ⋯

(Hint: Group powers x^3k, $x^{3 k - 1},$

and $x^{3 k - 2} .)$

(x + x^{2} - x^{3}) (1 + x^{3} + x^{6} + ⋯) = \frac{x + x^{2} - x^{3}}{1 - x^{3}}

x + x^{2} - x^{3} - x^{4} + x^{5} + x^{6} - x^{7} - x^{8} + ⋯

(Hint: Group powers x^4k, $x^{4 k - 1},$

etc.)

x - x^{2} - x^{3} + x^{4} - x^{5} - x^{6} + x^{7} - ⋯

(Hint: Group powers x^3k, $x^{3 k - 1},$

and $x^{3 k - 2} .)$

(x - x^{2} - x^{3}) (1 + x^{3} + x^{6} + ⋯) = \frac{x - x^{2} - x^{3}}{1 - x^{3}}

\frac{x}{2} + \frac{x^{2}}{4} - \frac{x^{3}}{8} + \frac{x^{4}}{16} + \frac{x^{5}}{32} - \frac{x^{6}}{64} + ⋯

(Hint: Group powers ${(\frac{x}{2})}^{3 k}, {(\frac{x}{2})}^{3 k - 1},$

and ${(\frac{x}{2})}^{3 k - 2} .)$

In the following exercises, find the power series of $f (x) g (x)$

given f and g as defined.

f (x) = 2 \sum_{n = 0}^{\infty} x^{n}, g (x) = \sum_{n = 0}^{\infty} n x^{n}

a_{n} = 2, b_{n} = n

so $c_{n} = \sum_{k = 0}^{n} b_{k} a_{n - k} = 2 \sum_{k = 0}^{n} k = (n) (n + 1)$

and $f (x) g (x) = \sum_{n = 1}^{\infty} n (n + 1) x^{n}$

f (x) = \sum_{n = 1}^{\infty} x^{n}, g (x) = \sum_{n = 1}^{\infty} \frac{1}{n} x^{n} .

Express the coefficients of $f (x) g (x)$

in terms of $H_{n} = \sum_{k = 1}^{n} \frac{1}{k} .$

f (x) = g (x) = \sum_{n = 1}^{\infty} {(\frac{x}{2})}^{n}

a_{n} = b_{n} = 2^{− n}

so $c_{n} = \sum_{k = 1}^{n} b_{k} a_{n - k} = 2^{− n} \sum_{k = 1}^{n} 1 = \frac{n}{2^{n}}$

and $f (x) g (x) = \sum_{n = 1}^{\infty} n {(\frac{x}{2})}^{n}$

f (x) = g (x) = \sum_{n = 1}^{\infty} n x^{n}

In the following exercises, differentiate the given series expansion of f term-by-term to obtain the corresponding series expansion for the derivative of f.

f (x) = \frac{1}{1 + x} = \sum_{n = 0}^{\infty} {(−1)}^{n} x^{n}

The derivative of $f$

is $- \frac{1}{{(1 + x)}^{2}} = − \sum_{n = 0}^{\infty} {(−1)}^{n} (n + 1) x^{n} .$

f (x) = \frac{1}{1 - x^{2}} = \sum_{n = 0}^{\infty} x^{2 n}

In the following exercises, integrate the given series expansion of $f$

term-by-term from zero to x to obtain the corresponding series expansion for the indefinite integral of $f .$

f (x) = \frac{2 x}{{(1 + x^{2})}^{2}} = \sum_{n = 1}^{\infty} {(−1)}^{n} (2 n) x^{2 n - 1}

The indefinite integral of $f$

is $\frac{1}{1 + x^{2}} = \sum_{n = 0}^{\infty} {(−1)}^{n} x^{2 n} .$

f (x) = \frac{2 x}{1 + x^{2}} = 2 \sum_{n = 0}^{\infty} {(−1)}^{n} x^{2 n + 1}

In the following exercises, evaluate each infinite series by identifying it as the value of a derivative or integral of geometric series.

Evaluate $\sum_{n = 1}^{\infty} \frac{n}{2^{n}}$

as $f^{'} (\frac{1}{2})$

where $f (x) = \sum_{n = 0}^{\infty} x^{n} .$

f (x) = \sum_{n = 0}^{\infty} x^{n} = \frac{1}{1 - x}; f^{'} (\frac{1}{2}) = \sum_{n = 1}^{\infty} \frac{n}{2^{n - 1}} = {\frac{d}{d x} {(1 - x)}^{−1} \|}_{x = 1 / 2} = {\frac{1}{{(1 - x)}^{2}} \|}_{x = 1 / 2} = 4

so $\sum_{n = 1}^{\infty} \frac{n}{2^{n}} = 2 .$

Evaluate $\sum_{n = 1}^{\infty} \frac{n}{3^{n}}$

as $f^{'} (\frac{1}{3})$

where $f (x) = \sum_{n = 0}^{\infty} x^{n} .$

Evaluate $\sum_{n = 2}^{\infty} \frac{n (n - 1)}{2^{n}}$

as $f ″ (\frac{1}{2})$

where $f (x) = \sum_{n = 0}^{\infty} x^{n} .$

f (x) = \sum_{n = 0}^{\infty} x^{n} = \frac{1}{1 - x}; f ″ (\frac{1}{2}) = \sum_{n = 2}^{\infty} \frac{n (n - 1)}{2^{n - 2}} = {\frac{d^{2}}{d x^{2}} {(1 - x)}^{−1} \|}_{x = 1 / 2} = {\frac{2}{{(1 - x)}^{3}} \|}_{x = 1 / 2} = 16

so $\sum_{n = 2}^{\infty} \frac{n (n - 1)}{2^{n}} = 4 .$

Evaluate $\sum_{n = 0}^{\infty} \frac{{(−1)}^{n}}{n + 1}$

as $\int_{0}^{1} f (t) d t$

where $f (x) = \sum_{n = 0}^{\infty} {(−1)}^{n} x^{2 n} = \frac{1}{1 + x^{2}} .$

In the following exercises, given that $\frac{1}{1 - x} = \sum_{n = 0}^{\infty} x^{n},$

use term-by-term differentiation or integration to find power series for each function centered at the given point.

f (x) = ln x

centered at $x = 1$

(Hint: $x = 1 - (1 - x))$

\int \sum {(1 - x)}^{n} d x = \int \sum {(−1)}^{n} {(x - 1)}^{n} d x = \sum \frac{{(−1)}^{n} {(x - 1)}^{n + 1}}{n + 1}

ln (1 - x)

at $x = 0$

ln (1 - x^{2})

at $x = 0$

− \int_{t = 0}^{x^{2}} \frac{1}{1 - t} d t = − \sum_{n = 0}^{\infty} \int_{0}^{x^{2}} t^{n} d x - \sum_{n = 0}^{\infty} \frac{x^{2 (n + 1)}}{n + 1} = − \sum_{n = 1}^{\infty} \frac{x^{2 n}}{n}

f (x) = \frac{2 x}{{(1 - x^{2})}^{2}}

at $x = 0$

f (x) = {tan}^{−1} (x^{2})

at $x = 0$

\int_{0}^{x^{2}} \frac{d t}{1 + t^{2}} = \sum_{n = 0}^{\infty} {(−1)}^{n} \int_{0}^{x^{2}} t^{2 n} d t = {\sum_{n = 0}^{\infty} {(−1)}^{n} \frac{t^{2 n + 1}}{2 n + 1} \|}_{t = 0}^{x^{2}} = \sum_{n = 0}^{\infty} {(−1)}^{n} \frac{x^{4 n + 2}}{2 n + 1}

f (x) = ln (1 + x^{2})

at $x = 0$

f (x) = \int_{0}^{x} ln t d t

where $ln (x) = \sum_{n = 1}^{\infty} {(−1)}^{n - 1} \frac{{(x - 1)}^{n}}{n}$

Term-by-term integration gives $\int_{0}^{x} ln t d t = \sum_{n = 1}^{\infty} {(−1)}^{n - 1} \frac{{(x - 1)}^{n + 1}}{n (n + 1)} = \sum_{n = 1}^{\infty} {(−1)}^{n - 1} (\frac{1}{n} - \frac{1}{n + 1}) {(x - 1)}^{n + 1} = (x - 1) ln x + \sum_{n = 2}^{\infty} {(−1)}^{n} \frac{{(x - 1)}^{n}}{n} = x ln x - x .$

[T] Evaluate the power series expansion $ln (1 + x) = \sum_{n = 1}^{\infty} {(−1)}^{n - 1} \frac{x^{n}}{n}$

at $x = 1$

to show that $ln (2)$

is the sum of the alternating harmonic series. Use the alternating series test to determine how many terms of the sum are needed to estimate $ln (2)$

accurate to within 0.001, and find such an approximation.

[T] Subtract the infinite series of $ln (1 - x)$

from $ln (1 + x)$

to get a power series for $ln (\frac{1 + x}{1 - x}) .$

Evaluate at $x = \frac{1}{3} .$

What is the smallest N such that the Nth partial sum of this series approximates $ln (2)$

with an error less than 0.001?

We have $ln (1 - x) = − \sum_{n = 1}^{\infty} \frac{x^{n}}{n}$

so $ln (1 + x) = \sum_{n = 1}^{\infty} {(−1)}^{n - 1} \frac{x^{n}}{n} .$

Thus, $ln (\frac{1 + x}{1 - x}) = \sum_{n = 1}^{\infty} (1 + {(−1)}^{n - 1}) \frac{x^{n}}{n} = 2 \sum_{n = 1}^{\infty} \frac{x^{2 n - 1}}{2 n - 1} .$

When $x = \frac{1}{3}$

we obtain $ln (2) = 2 \sum_{n = 1}^{\infty} \frac{1}{3^{2 n - 1} (2 n - 1)} .$

We have $2 \sum_{n = 1}^{3} \frac{1}{3^{2 n - 1} (2 n - 1)} = 0.69300 …,$

while $2 \sum_{n = 1}^{4} \frac{1}{3^{2 n - 1} (2 n - 1)} = 0.69313 …$

and $ln (2) = 0.69314 …;$

therefore, $N = 4 .$

In the following exercises, using a substitution if indicated, express each series in terms of elementary functions and find the radius of convergence of the sum.

\sum_{k = 0}^{\infty} (x^{k} - x^{2 k + 1})

\sum_{k = 1}^{\infty} \frac{x^{3 k}}{6 k}

\sum_{k = 1}^{\infty} \frac{x^{k}}{k} = − ln (1 - x)

so $\sum_{k = 1}^{\infty} \frac{x^{3 k}}{6 k} = - \frac{1}{6} ln (1 - x^{3}) .$

The radius of convergence is equal to 1 by the ratio test.

\sum_{k = 1}^{\infty} {(1 + x^{2})}^{− k}

using $y = \frac{1}{1 + x^{2}}$

\sum_{k = 1}^{\infty} 2^{− k x}

using $y = 2^{− x}$

If $y = 2^{− x},$

then $\sum_{k = 1}^{\infty} y^{k} = \frac{y}{1 - y} = \frac{2^{− x}}{1 - 2^{− x}} = \frac{1}{2^{x} - 1} .$

If $a_{k} = 2^{− k x},$

then $\frac{a_{k + 1}}{a_{k}} = 2^{− x} < 1$

when $x > 0 .$

So the series converges for all $x > 0 .$

Show that, up to powers x³ and y³, $E (x) = \sum_{n = 0}^{\infty} \frac{x^{n}}{n!}$

satisfies $E (x + y) = E (x) E (y) .$

Differentiate the series $E (x) = \sum_{n = 0}^{\infty} \frac{x^{n}}{n!}$

term-by-term to show that $E (x)$

is equal to its derivative.

Answers will vary.

Show that if $f (x) = \sum_{n = 0}^{\infty} a_{n} x^{n}$

is a sum of even powers, that is, $a_{n} = 0$

if n is odd, then $F = \int_{0}^{x} f (t) d t$

is a sum of odd powers, while if f is a sum of odd powers, then F is a sum of even powers.

[T] Suppose that the coefficients a_n of the series $\sum_{n = 0}^{\infty} a_{n} x^{n}$

are defined by the recurrence relation $a_{n} = \frac{a_{n - 1}}{n} + \frac{a_{n - 2}}{n (n - 1)} .$

For $a_{0} = 0$

and $a_{1} = 1,$

compute and plot the sums $S_{N} = \sum_{n = 0}^{N} a_{n} x^{n}$

for $N = 2, 3, 4, 5$

on $[−1, 1] .$

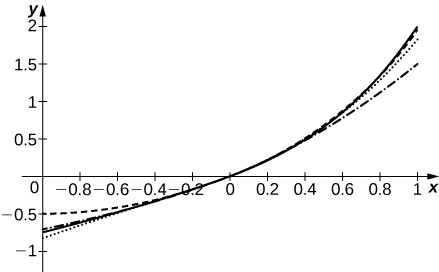
This is a graph of three curves. They are all increasing and become very close as the curves approach x = 0. Then they separate as x moves away from 0.

The solid curve is S₅. The dashed curve is S₂, dotted is S₃, and dash-dotted is S₄

[T] Suppose that the coefficients a_n of the series $\sum_{n = 0}^{\infty} a_{n} x^{n}$

are defined by the recurrence relation $a_{n} = \frac{a_{n - 1}}{\sqrt{n}} - \frac{a_{n - 2}}{\sqrt{n (n - 1)}} .$

For $a_{0} = 1$

and $a_{1} = 0,$

compute and plot the sums $S_{N} = \sum_{n = 0}^{N} a_{n} x^{n}$

for $N = 2, 3, 4, 5$

on $[−1, 1] .$

[T] Given the power series expansion $ln (1 + x) = \sum_{n = 1}^{\infty} {(−1)}^{n - 1} \frac{x^{n}}{n},$

determine how many terms N of the sum evaluated at $x = −1 / 2$

are needed to approximate $ln (2)$

accurate to within 1/1000. Evaluate the corresponding partial sum $\sum_{n = 1}^{N} {(−1)}^{n - 1} \frac{x^{n}}{n} .$

When $x = - \frac{1}{2}, − ln (2) = ln (\frac{1}{2}) = − \sum_{n = 1}^{\infty} \frac{1}{n 2^{n}} .$

Since $\sum_{n = 11}^{\infty} \frac{1}{n 2^{n}} < \sum_{n = 11}^{\infty} \frac{1}{2^{n}} = \frac{1}{2^{10}},$

one has $\sum_{n = 1}^{10} \frac{1}{n 2^{n}} = 0.69306 …$

whereas $ln (2) = 0.69314 …;$

therefore, $N = 10 .$

[T] Given the power series expansion ${tan}^{−1} (x) = \sum_{k = 0}^{\infty} {(−1)}^{k} \frac{x^{2 k + 1}}{2 k + 1},$

use the alternating series test to determine how many terms N of the sum evaluated at $x = 1$

are needed to approximate ${tan}^{−1} (1) = \frac{π}{4}$

accurate to within 1/1000. Evaluate the corresponding partial sum $\sum_{k = 0}^{N} {(−1)}^{k} \frac{x^{2 k + 1}}{2 k + 1} .$

[T] Recall that ${tan}^{−1} (\frac{1}{\sqrt{3}}) = \frac{π}{6} .$

Assuming an exact value of $(\frac{1}{\sqrt{3}}),$

estimate $\frac{π}{6}$

by evaluating partial sums $S_{N} (\frac{1}{\sqrt{3}})$

of the power series expansion ${tan}^{−1} (x) = \sum_{k = 0}^{\infty} {(−1)}^{k} \frac{x^{2 k + 1}}{2 k + 1}$

at $x = \frac{1}{\sqrt{3}} .$

What is the smallest number N such that $6 S_{N} (\frac{1}{\sqrt{3}})$

approximates π accurately to within 0.001? How many terms are needed for accuracy to within 0.00001?

6 S_{N} (\frac{1}{\sqrt{3}}) = 2 \sqrt{3} \sum_{n = 0}^{N} {(−1)}^{n} \frac{1}{3^{n} (2 n + 1)} .

One has $π - 6 S_{4} (\frac{1}{\sqrt{3}}) = 0.00101 …$

and $π - 6 S_{5} (\frac{1}{\sqrt{3}}) = 0.00028 …$

so $N = 5$

is the smallest partial sum with accuracy to within 0.001. Also, $π - 6 S_{7} (\frac{1}{\sqrt{3}}) = 0.00002 …$

while $π - 6 S_{8} (\frac{1}{\sqrt{3}}) = −0.000007 …$

so $N = 8$

is the smallest N to give accuracy to within 0.00001.

Properties of Power Series

Combining Power Series

Proof

Multiplication of Power Series

Differentiating and Integrating Power Series

Proof

Key Concepts

Glossary