A power series is a type of series with terms involving a variable. More specifically, if the variable is x, then all the terms of the series involve powers of x. As a result, a power series can be thought of as an infinite polynomial. Power series are used to represent common functions and also to define new functions. In this section we define power series and show how to determine when a power series converges and when it diverges. We also show how to represent certain functions using power series.
A series of the form
where x is a variable and the coefficients cn are constants, is known as a power series. The series
is an example of a power series. Since this series is a geometric series with ratio
we know that it converges if
and diverges if
A series of the form
is a power series centered at
A series of the form
is a power series centered at
To make this definition precise, we stipulate that
and
even when
and
respectively.
The series
and
are both power series centered at
The series
is a power series centered at
Since the terms in a power series involve a variable x, the series may converge for certain values of x and diverge for other values of x. For a power series centered at
the value of the series at
is given by
Therefore, a power series always converges at its center. Some power series converge only at that value of x. Most power series, however, converge for more than one value of x. In that case, the power series either converges for all real numbers x or converges for all x in a finite interval. For example, the geometric series
converges for all x in the interval
but diverges for all x outside that interval. We now summarize these three possibilities for a general power series.
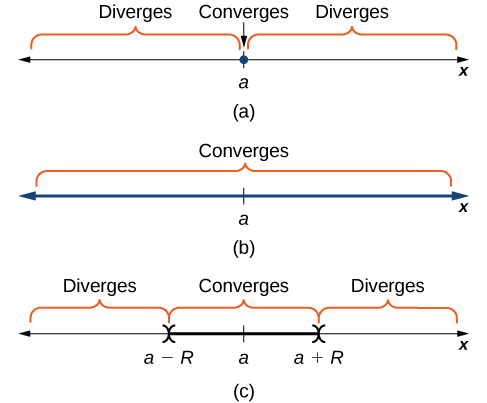
Consider the power series
The series satisfies exactly one of the following properties:
and diverges for all
such that the series converges if
and diverges if
At the values x where
the series may converge or diverge.
Suppose that the power series is centered at
(For a series centered at a value of a other than zero, the result follows by letting
and considering the series
We must first prove the following fact:
If there exists a real number
such that
converges, then the series
converges absolutely for all x such that
Since
converges, the nth term
as
Therefore, there exists an integer N such that
for all
Writing
we conclude that, for all
The series
is a geometric series that converges if
Therefore, by the comparison test, we conclude that
also converges for
Since we can add a finite number of terms to a convergent series, we conclude that
converges for
With this result, we can now prove the theorem. Consider the series
and let S be the set of real numbers for which the series converges. Suppose that the set
Then the series falls under case i. Suppose that the set S is the set of all real numbers. Then the series falls under case ii. Suppose that
and S is not the set of real numbers. Then there exists a real number
such that the series does not converge. Thus, the series cannot converge for any x such that
Therefore, the set S must be a bounded set, which means that it must have a smallest upper bound. (This fact follows from the Least Upper Bound Property for the real numbers, which is beyond the scope of this text and is covered in real analysis courses.) Call that smallest upper bound R. Since
the number
Therefore, the series converges for all x such that
and the series falls into case iii.
□
If a series
falls into case iii. of [link], then the series converges for all x such that
for some
and diverges for all x such that
The series may converge or diverge at the values x where
The set of values x for which the series
converges is known as the interval of convergence. Since the series diverges for all values x where
the length of the interval is 2R, and therefore, the radius of the interval is R. The value R is called the radius of convergence. For example, since the series
converges for all values x in the interval
and diverges for all values x such that
the interval of convergence of this series is
Since the length of the interval is 2, the radius of convergence is 1.
Consider the power series
The set of real numbers x where the series converges is the interval of convergence. If there exists a real number
such that the series converges for
and diverges for
then R is the radius of convergence. If the series converges only at
we say the radius of convergence is
If the series converges for all real numbers x, we say the radius of convergence is
([link]).

To determine the interval of convergence for a power series, we typically apply the ratio test. In [link], we show the three different possibilities illustrated in [link].
For each of the following series, find the interval and radius of convergence.
for all values of x. Therefore, the series converges for all real numbers x. The interval of convergence is
and the radius of convergence is
we see that
Therefore, the series diverges for all
Since the series is centered at
it must converge there, so the series converges only for
The interval of convergence is the single value
and the radius of convergence is
The ratio
if
Since
implies that
the series converges absolutely if
The ratio
if
Therefore, the series diverges if
or
The ratio test is inconclusive if
The ratio
if and only if
or
We need to test these values of x separately. For
the series is given by
Since this is the alternating harmonic series, it converges. Thus, the series converges at
For
the series is given by
This is the harmonic series, which is divergent. Therefore, the power series diverges at
We conclude that the interval of convergence is
and the radius of convergence is
Find the interval and radius of convergence for the series
The interval of convergence is
The radius of convergence is
Apply the ratio test to check for absolute convergence.
Being able to represent a function by an “infinite polynomial” is a powerful tool. Polynomial functions are the easiest functions to analyze, since they only involve the basic arithmetic operations of addition, subtraction, multiplication, and division. If we can represent a complicated function by an infinite polynomial, we can use the polynomial representation to differentiate or integrate it. In addition, we can use a truncated version of the polynomial expression to approximate values of the function. So, the question is, when can we represent a function by a power series?
Consider again the geometric series
Recall that the geometric series
converges if and only if
In that case, it converges to
Therefore, if
the series in [link] converges to
and we write
As a result, we are able to represent the function
by the power series
We now show graphically how this series provides a representation for the function
by comparing the graph of f with the graphs of several of the partial sums of this infinite series.
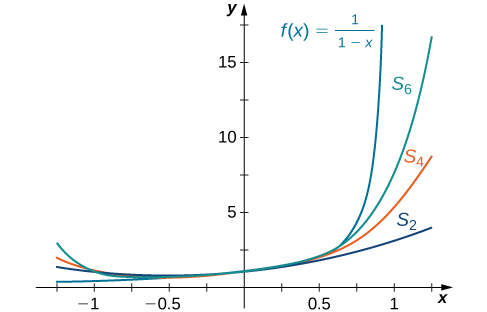
Sketch a graph of
and the graphs of the corresponding partial sums
for
on the interval
Comment on the approximation
as N increases.
From the graph in [link] you see that as N increases,
becomes a better approximation for
for x in the interval
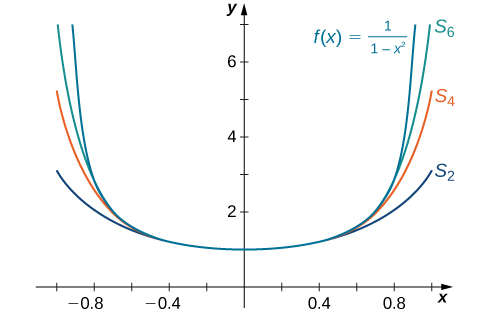
Sketch a graph of
and the corresponding partial sums
for
on the interval
Next we consider functions involving an expression similar to the sum of a geometric series and show how to represent these functions using power series.
Use a power series to represent each of the following functions
Find the interval of convergence.
Using the fact that, for
is the sum of the geometric series
we see that, for
Since this series converges if and only if
the interval of convergence is
and we have
Therefore, we have
The series converges as long as
(note that when
the series does not converge). Solving this inequality, we conclude that the interval of convergence is
and
for
Represent the function
using a power series and find the interval of convergence.
with interval of convergence
Rewrite f in the form
for some functions g and h.
In the remaining sections of this chapter, we will show ways of deriving power series representations for many other functions, and how we can make use of these representations to evaluate, differentiate, and integrate various functions.
one of the following three properties hold:
In this case, we say that the radius of convergence is
and diverges for
In this case, the radius of convergence is R.
for
allows us to represent certain functions using geometric series.
In the following exercises, state whether each statement is true, or give an example to show that it is false.
If
converges, then
as
True. If a series converges then its terms tend to zero.
converges at
for any real numbers
Given any sequence
there is always some
possibly very small, such that
converges on
False. It would imply that
for
If
then
does not tend to zero for any
If
has radius of convergence
and if
for all n, then the radius of convergence of
is greater than or equal to R.
Suppose that
converges at
At which of the following points must the series also converge? Use the fact that if
converges at x, then it converges at any point closer to c than x.
It must converge on
and hence at: a.
b.
c.
d.
e.
and f.
Suppose that
converges at
At which of the following points must the series also converge? Use the fact that if
converges at x, then it converges at any point closer to c than x.
In the following exercises, suppose that
as
Find the radius of convergence for each series.
so
so
so
In the following exercises, find the radius of convergence R and interval of convergence for
with the given coefficients
so
so
When
the series is harmonic and diverges. When
the series is alternating harmonic and converges. The interval of convergence is
so
so
When
the series diverges by the divergence test. The interval of convergence is
so
When
the series diverges by the divergence test. The interval of convergence is
so
When
the series is an absolutely convergent p-series. The interval of convergence is
so the series converges for all x by the ratio test and
In the following exercises, find the radius of convergence of each series.
so
so
so
so
where
so
so
In the following exercises, use the ratio test to determine the radius of convergence of each series.
so
so
so
In the following exercises, given that
with convergence in
find the power series for each function with the given center a, and identify its interval of convergence.
(Hint:
on
on
on
on
on
Use the next exercise to find the radius of convergence of the given series in the subsequent exercises.
Explain why, if
then
whenever
and, therefore, the radius of convergence of
is
as
and
when
Therefore,
converges when
by the nth root test.
so
so
so
so
Suppose that
such that
if n is even. Explain why
Suppose that
such that
if n is odd. Explain why
We can rewrite
and
since
Suppose that
converges on
Find the interval of convergence of
Suppose that
converges on
Find the interval of convergence of
If
then
so
converges.
In the following exercises, suppose that
satisfies
where
for each n. State whether each series converges on the full interval
or if there is not enough information to draw a conclusion. Use the comparison test when appropriate.
Converges on
by the ratio test
(Hint: Let
if
for some n, otherwise
Consider the series
where
if
and
otherwise. Then
and so the series converges on
by the comparison test.
Suppose that
is a polynomial of degree N. Find the radius and interval of convergence of
[T] Plot the graphs of
and of the partial sums
for
on the interval
Comment on the approximation of
by
near
and near
as N increases.
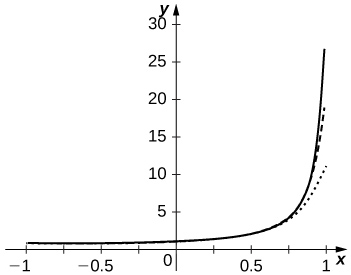
The approximation is more accurate near
The partial sums follow
more closely as N increases but are never accurate near
since the series diverges there.
[T] Plot the graphs of
and of the partial sums
for
on the interval
Comment on the behavior of the sums near
and near
as N increases.
[T] Plot the graphs of the partial sums
for
on the interval
Comment on the behavior of the sums near
and near
as N increases.
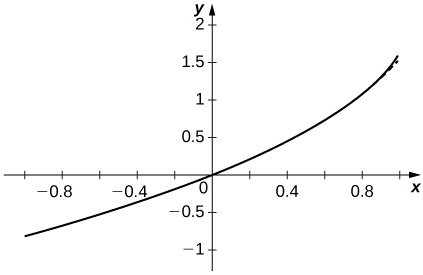
The approximation appears to stabilize quickly near both
[T] Plot the graphs of the partial sums
for
on the interval
Comment on the behavior of the sums near
and near
as N increases.
[T] Plot the graphs of the partial sums
for
on the interval
Comment on how these plots approximate
as N increases.
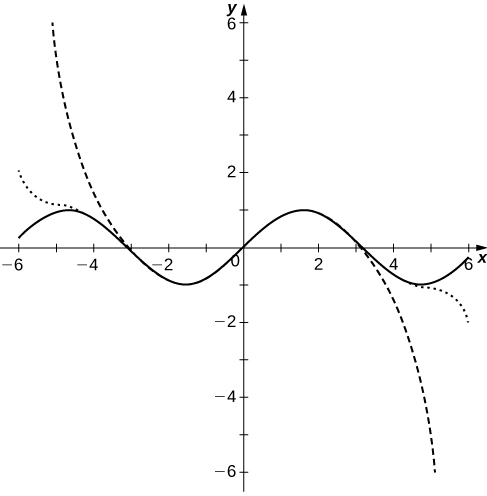
The polynomial curves have roots close to those of
up to their degree and then the polynomials diverge from
[T] Plot the graphs of the partial sums
for
on the interval
Comment on how these plots approximate
as N increases.
is a power series centered at
a series of the form
is a power series centered at
such that a power series centered at
converges for
and diverges for
then R is the radius of convergence; if the power series only converges at
the radius of convergence is
if the power series converges for all real numbers x, the radius of convergence is

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: