![The sum of the areas of the rectangles is greater than the area between the curve f(x)=1/x and the x-axis for x≥1. Since the area bounded by the curve is infinite (as calculated by an improper integral), the sum of the areas of the rectangles is also infinite. This is a graph in quadrant 1 of a decreasing concave up curve approaching the x axis – f(x) = 1/x. Five rectangles are drawn with base 1 over the interval [1, 6]. The height of each rectangle is determined by the value of the function at the left endpoint of the rectangle’s base. The areas for each are marked: 1, 1/2, 1/3, 1/4, and 1/5.](../resources/CNX_Calc_Figure_09_03_001.jpg)
In the previous section, we determined the convergence or divergence of several series by explicitly calculating the limit of the sequence of partial sums
In practice, explicitly calculating this limit can be difficult or impossible. Luckily, several tests exist that allow us to determine convergence or divergence for many types of series. In this section, we discuss two of these tests: the divergence test and the integral test. We will examine several other tests in the rest of this chapter and then summarize how and when to use them.
For a series
to converge, the
term
must satisfy
as
Therefore, from the algebraic limit properties of sequences,
Therefore, if
converges, the
term
as
An important consequence of this fact is the following statement:
This test is known as the divergence test because it provides a way of proving that a series diverges.
If
or
does not exist, then the series
diverges.
It is important to note that the converse of this theorem is not true. That is, if
we cannot make any conclusion about the convergence of
For example,
but the harmonic series
diverges. In this section and the remaining sections of this chapter, we show many more examples of such series. Consequently, although we can use the divergence test to show that a series diverges, we cannot use it to prove that a series converges. Specifically, if
the divergence test is inconclusive.
For each of the following series, apply the divergence test. If the divergence test proves that the series diverges, state so. Otherwise, indicate that the divergence test is inconclusive.
by the divergence test, we can conclude that
diverges.
the divergence test is inconclusive.
by the divergence test, the series
diverges.
What does the divergence test tell us about the series
The series diverges.
Look at
In the previous section, we proved that the harmonic series diverges by looking at the sequence of partial sums
and showing that
for all positive integers
In this section we use a different technique to prove the divergence of the harmonic series. This technique is important because it is used to prove the divergence or convergence of many other series. This test, called the integral test, compares an infinite sum to an improper integral. It is important to note that this test can only be applied when we are considering a series whose terms are all positive.
To illustrate how the integral test works, use the harmonic series as an example. In [link], we depict the harmonic series by sketching a sequence of rectangles with areas
along with the function
From the graph, we see that
Therefore, for each
the
partial sum
satisfies
Since
we see that the sequence of partial sums
is unbounded. Therefore,
diverges, and, consequently, the series
also diverges.
![The sum of the areas of the rectangles is greater than the area between the curve f(x)=1/x and the x-axis for x≥1. Since the area bounded by the curve is infinite (as calculated by an improper integral), the sum of the areas of the rectangles is also infinite. This is a graph in quadrant 1 of a decreasing concave up curve approaching the x axis – f(x) = 1/x. Five rectangles are drawn with base 1 over the interval [1, 6]. The height of each rectangle is determined by the value of the function at the left endpoint of the rectangle’s base. The areas for each are marked: 1, 1/2, 1/3, 1/4, and 1/5.](../resources/CNX_Calc_Figure_09_03_001.jpg)
Now consider the series
We show how an integral can be used to prove that this series converges. In [link], we sketch a sequence of rectangles with areas
along with the function
From the graph we see that
Therefore, for each
the
partial sum
satisfies
We conclude that the sequence of partial sums
is bounded. We also see that
is an increasing sequence:
Since
is increasing and bounded, by the Monotone Convergence Theorem, it converges. Therefore, the series
converges.
![The sum of the areas of the rectangles is less than the sum of the area of the first rectangle and the area between the curve f(x)=1/x2 and the x-axis for x≥1. Since the area bounded by the curve is finite, the sum of the areas of the rectangles is also finite. This is a graph in quadrant 1 of the decreasing concave up curve f(x) = 1/(x^2), which approaches the x axis. Rectangles of base 1 are drawn over the interval [0, 5]. The height of each rectangle is determined by the value of the function at the right endpoint of its base. The areas of each are marked: 1, 1/(2^2), 1/(3^2), 1/(4^2) and 1/(5^2).](../resources/CNX_Calc_Figure_09_03_004.jpg)
We can extend this idea to prove convergence or divergence for many different series. Suppose
is a series with positive terms
such that there exists a continuous, positive, decreasing function
where
for all positive integers. Then, as in [link](a), for any integer
the
partial sum
satisfies
Therefore, if
converges, then the sequence of partial sums
is bounded. Since
is an increasing sequence, if it is also a bounded sequence, then by the Monotone Convergence Theorem, it converges. We conclude that if
converges, then the series
also converges. On the other hand, from [link](b), for any integer
the
partial sum
satisfies
If
then
is an unbounded sequence and therefore diverges. As a result, the series
also diverges. Since
is a positive function, if
diverges, then
We conclude that if
diverges, then
diverges.
![(a) If we can inscribe rectangles inside a region bounded by a curve y=f(x) and the x-axis, and the area bounded by those curves for x≥1 is finite, then the sum of the areas of the rectangles is also finite. (b) If a set of rectangles circumscribes the region bounded by y=f(x) and the x axis for x≥1 and the region has infinite area, then the sum of the areas of the rectangles is also infinite. This shows two graphs side by side of the same function y = f(x), a decreasing concave up curve approaching the x axis. Rectangles are drawn with base 1 over the intervals [0, 6] and [1, 6]. For the graph on the left, the height of each rectangle is determined by the value of the function at the right endpoint of its base. For the graph on the right, the height of each rectangle is determined by the value of the function at the left endpoint of its base. Areas a_1 through a_6 are marked in the graph on the left, and the same for a_1 to a_5 on the right.](../resources/CNX_Calc_Figure_09_03_002.jpg)
Suppose
is a series with positive terms
Suppose there exists a function
and a positive integer
such that the following three conditions are satisfied:
is continuous,
is decreasing, and
for all integers
Then
both converge or both diverge (see [link]).
Although convergence of
implies convergence of the related series
it does not imply that the value of the integral and the series are the same. They may be different, and often are. For example,
is a geometric series with initial term
and ratio
which converges to
However, the related integral
satisfies
For each of the following series, use the integral test to determine whether the series converges or diverges.
We have
Thus the integral
converges, and therefore so does the series
Since
the integral
diverges, and therefore
diverges.
Use the integral test to determine whether the series
converges or diverges.
The series diverges.
Compare to the integral
The harmonic series
and the series
are both examples of a type of series called a p-series.
For any real number
the series
is called a p-series.
We know the p-series converges if
and diverges if
What about other values of
In general, it is difficult, if not impossible, to compute the exact value of most
-series. However, we can use the tests presented thus far to prove whether a
-series converges or diverges.
If
then
and if
then
Therefore, by the divergence test,
If
then
is a positive, continuous, decreasing function. Therefore, for
we use the integral test, comparing
We have already considered the case when
Here we consider the case when
For this case,
Because
we conclude that
Therefore,
converges if
and diverges if
In summary,
For each of the following series, determine whether it converges or diverges.
so the series converges.
the series diverges.
Does the series
converge or diverge?
The series converges.
Suppose we know that a series
converges and we want to estimate the sum of that series. Certainly we can approximate that sum using any finite sum
where
is any positive integer. The question we address here is, for a convergent series
how good is the approximation
More specifically, if we let
be the remainder when the sum of an infinite series is approximated by the
partial sum, how large is
For some types of series, we are able to use the ideas from the integral test to estimate
Suppose
is a convergent series with positive terms. Suppose there exists a function
satisfying the following three conditions:
is continuous,
is decreasing, and
for all integers
Let
be the Nth partial sum of
For all positive integers
In other words, the remainder
satisfies the following estimate:
This is known as the remainder estimate.
We illustrate [link] in [link]. In particular, by representing the remainder
as the sum of areas of rectangles, we see that the area of those rectangles is bounded above by
and bounded below by
In other words,
and
We conclude that
Since
where
is the
partial sum, we conclude that
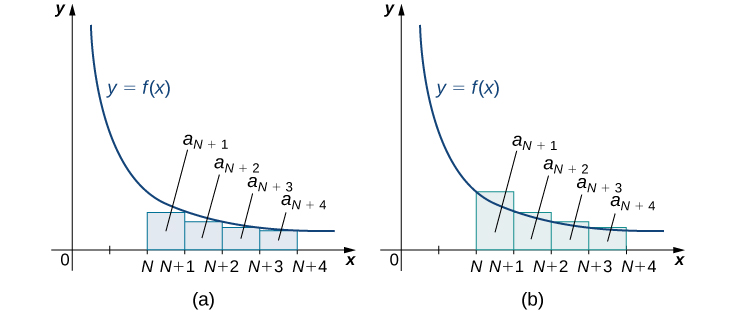
Consider the series
and estimate the error.
necessary such that
will estimate
to within
By the remainder estimate, we know
We have
Therefore, the error is
such that
In part a. we showed that
Therefore, the remainder
as long as
That is, we need
Solving this inequality for
we see that we need
To ensure that the remainder is within the desired amount, we need to round up to the nearest integer. Therefore, the minimum necessary value is
For
calculate
and estimate the error
Use the remainder estimate
then the series
diverges.
the series
may converge or diverge.
is a series with positive terms
and
is a continuous, decreasing function such that
for all positive integers
then
either both converge or both diverge. Furthermore, if
converges, then the
partial sum approximation
is accurate up to an error
where
converges if
and diverges if
For each of the following sequences, if the divergence test applies, either state that
does not exist or find
If the divergence test does not apply, state why.
Divergence test does not apply.
Series diverges.
(does not exist). Series diverges.
Series diverges.
does not exist. Series diverges.
Series diverges.
Divergence test does not apply.
State whether the given
-series converges.
Series converges,
Series converges,
Series converges,
Use the integral test to determine whether the following sums converge.
Series diverges by comparison with
Series diverges by comparison with
Series converges by comparison with
Express the following sums as
-series and determine whether each converges.
(Hint:
.)
Since
diverges by
-series.
(Hint:
.)
Since
diverges by
-series.
Use the estimate
to find a bound for the remainder
where
[T] Find the minimum value of
such that the remainder estimate
guarantees that
estimates
accurate to within the given error.
error
error
error
error
error
In the following exercises, find a value of
such that
is smaller than the desired error. Compute the corresponding sum
and compare it to the given estimate of the infinite series.
error
error
okay if
Estimate agrees with
to five decimal places.
error
error
okay if
Estimate agrees with the sum to four decimal places.
error
Find the limit as
of
(Hint: Compare to
Find the limit as
of
The next few exercises are intended to give a sense of applications in which partial sums of the harmonic series arise.
In certain applications of probability, such as the so-called Watterson estimator for predicting mutation rates in population genetics, it is important to have an accurate estimate of the number
Recall that
is decreasing. Compute
to four decimal places. (Hint:
.)
[T] Complete sampling with replacement, sometimes called the coupon collector’s problem, is phrased as follows: Suppose you have
unique items in a bin. At each step, an item is chosen at random, identified, and put back in the bin. The problem asks what is the expected number of steps
that it takes to draw each unique item at least once. It turns out that
Find
for
[T] The simplest way to shuffle cards is to take the top card and insert it at a random place in the deck, called top random insertion, and then repeat. We will consider a deck to be randomly shuffled once enough top random insertions have been made that the card originally at the bottom has reached the top and then been randomly inserted. If the deck has
cards, then the probability that the insertion will be below the card initially at the bottom (call this card
is
Thus the expected number of top random insertions before
is no longer at the bottom is n. Once one card is below
there are two places below
and the probability that a randomly inserted card will fall below
is
The expected number of top random insertions before this happens is
The two cards below
are now in random order. Continuing this way, find a formula for the expected number of top random insertions needed to consider the deck to be randomly shuffled.
The expected number of random insertions to get
to the top is
Then one more insertion puts
back in at random. Thus, the expected number of shuffles to randomize the deck is
Suppose a scooter can travel
km on a full tank of fuel. Assuming that fuel can be transferred from one scooter to another but can only be carried in the tank, present a procedure that will enable one of the scooters to travel
km, where
Show that for the remainder estimate to apply on
it is sufficient that
be decreasing on
but
need not be decreasing on
Set
and
such that
is decreasing on
[T] Use the remainder estimate and integration by parts to approximate
within an error smaller than
Does
converge if
is large enough? If so, for which
The series converges for
by integral test using change of variable.
[T] Suppose a computer can sum one million terms per second of the divergent series
Use the integral test to approximate how many seconds it will take to add up enough terms for the partial sum to exceed
[T] A fast computer can sum one million terms per second of the divergent series
Use the integral test to approximate how many seconds it will take to add up enough terms for the partial sum to exceed
terms are needed.
then the series
diverges
with positive terms
if there exists a continuous, decreasing function
such that
for all positive integers
then
either both converge or both diverge
with positive terms
and a continuous, decreasing function
such that
for all positive integers
the remainder
satisfies the following estimate:

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: