So far in this chapter, we have primarily discussed series with positive terms. In this section we introduce alternating series—those series whose terms alternate in sign. We will show in a later chapter that these series often arise when studying power series. After defining alternating series, we introduce the alternating series test to determine whether such a series converges.
A series whose terms alternate between positive and negative values is an alternating series. For example, the series
and
are both alternating series.
Any series whose terms alternate between positive and negative values is called an alternating series. An alternating series can be written in the form
or
Where
for all positive integers n.
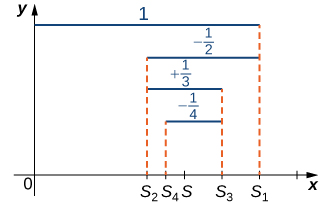
Series (1), shown in [link], is a geometric series. Since
the series converges. Series (2), shown in [link], is called the alternating harmonic series. We will show that whereas the harmonic series diverges, the alternating harmonic series converges.
To prove this, we look at the sequence of partial sums
([link]).
Consider the odd terms
for
Since
Therefore,
is a decreasing sequence. Also,
Therefore,
is bounded below. Since
is a decreasing sequence that is bounded below, by the Monotone Convergence Theorem,
converges. Similarly, the even terms
form an increasing sequence that is bounded above because
and
Therefore, by the Monotone Convergence Theorem, the sequence
also converges. Since
we know that
Letting
and using the fact that
we conclude that
Since the odd terms and the even terms in the sequence of partial sums converge to the same limit
it can be shown that the sequence of partial sums converges to
and therefore the alternating harmonic series converges to
It can also be shown that
and we can write

□
More generally, any alternating series of form (3) ([link]) or (4) ([link]) converges as long as
and
([link]). The proof is similar to the proof for the alternating harmonic series.
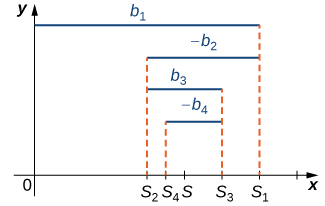
An alternating series of the form
converges if
for all
and
This is known as the alternating series test.
We remark that this theorem is true more generally as long as there exists some integer
such that
for all
For each of the following alternating series, determine whether the series converges or diverges.
the series converges.
as
we cannot apply the alternating series test. Instead, we use the nth term test for divergence. Since
the series diverges.
Determine whether the series
converges or diverges.
The series converges.
Is
decreasing? What is
It is difficult to explicitly calculate the sum of most alternating series, so typically the sum is approximated by using a partial sum. When doing so, we are interested in the amount of error in our approximation. Consider an alternating series
satisfying the hypotheses of the alternating series test. Let
denote the sum of this series and
be the corresponding sequence of partial sums. From [link], we see that for any integer
the remainder
satisfies
Consider an alternating series of the form
that satisfies the hypotheses of the alternating series test. Let
denote the sum of the series and
denote the
partial sum. For any integer
the remainder
satisfies
In other words, if the conditions of the alternating series test apply, then the error in approximating the infinite series by the
partial sum
is in magnitude at most the size of the next term
Consider the alternating series
Use the remainder estimate to determine a bound on the error
if we approximate the sum of the series by the partial sum
From the theorem stated above,
Find a bound for
when approximating
by
Consider a series
and the related series
Here we discuss possibilities for the relationship between the convergence of these two series. For example, consider the alternating harmonic series
The series whose terms are the absolute value of these terms is the harmonic series, since
Since the alternating harmonic series converges, but the harmonic series diverges, we say the alternating harmonic series exhibits conditional convergence.
By comparison, consider the series
The series whose terms are the absolute values of the terms of this series is the series
Since both of these series converge, we say the series
exhibits absolute convergence.
A series
exhibits absolute convergence if
converges. A series
exhibits conditional convergence if
converges but
diverges.
As shown by the alternating harmonic series, a series
may converge, but
may diverge. In the following theorem, however, we show that if
converges, then
converges.
If
converges, then
converges.
Suppose that
converges. We show this by using the fact that
or
and therefore
or
Therefore,
Consequently, by the comparison test, since
converges, the series
converges. By using the algebraic properties for convergent series, we conclude that
converges.
□
For each of the following series, determine whether the series converges absolutely, converges conditionally, or diverges.
diverges by using the limit comparison test with the harmonic series. In fact,
Therefore, the series does not converge absolutely. However, since
the series converges. We can conclude that
converges conditionally.
to determine whether the series converges absolutely, compare
with the series
Since
converges, by the comparison test,
converges, and therefore
converges absolutely.
Determine whether the series
converges absolutely, converges conditionally, or diverges.
The series converges absolutely.
Check for absolute convergence first.
To see the difference between absolute and conditional convergence, look at what happens when we rearrange the terms of the alternating harmonic series
We show that we can rearrange the terms so that the new series diverges. Certainly if we rearrange the terms of a finite sum, the sum does not change. When we work with an infinite sum, however, interesting things can happen.
Begin by adding enough of the positive terms to produce a sum that is larger than some real number
For example, let
and find an integer
such that
(We can do this because the series
diverges to infinity.) Then subtract
Then add more positive terms until the sum reaches 100. That is, find another integer
such that
Then subtract
Continuing in this way, we have found a way of rearranging the terms in the alternating harmonic series so that the sequence of partial sums for the rearranged series is unbounded and therefore diverges.
The terms in the alternating harmonic series can also be rearranged so that the new series converges to a different value. In [link], we show how to rearrange the terms to create a new series that converges to
We point out that the alternating harmonic series can be rearranged to create a series that converges to any real number
however, the proof of that fact is beyond the scope of this text.
In general, any series
that converges conditionally can be rearranged so that the new series diverges or converges to a different real number. A series that converges absolutely does not have this property. For any series
that converges absolutely, the value of
is the same for any rearrangement of the terms. This result is known as the Riemann Rearrangement Theorem, which is beyond the scope of this book.
Use the fact that
to rearrange the terms in the alternating harmonic series so the sum of the rearranged series is
Let
Since
by the algebraic properties of convergent series,
Now introduce the series
such that for all
and
Then
Then using the algebraic limit properties of convergent series, since
and
converge, the series
converges and
Now adding the corresponding terms,
and
we see that
We notice that the series on the right side of the equal sign is a rearrangement of the alternating harmonic series. Since
we conclude that
Therefore, we have found a rearrangement of the alternating harmonic series having the desired property.
if
for all
and
as
the alternating series converges.
converges, then
converges.
State whether each of the following series converges absolutely, conditionally, or not at all.
Does not converge by divergence test. Terms do not tend to zero.
Converges conditionally by alternating series test, since
is decreasing. Does not converge absolutely by comparison with p-series,
Converges absolutely by limit comparison to
for example.
Diverges by divergence test since
Does not converge. Terms do not tend to zero.
Diverges by divergence test.
Converges by alternating series test.
Converges conditionally by alternating series test. Does not converge absolutely by limit comparison with p-series,
Diverges; terms do not tend to zero.
(Hint:
for large
(Hint:
for large
Converges by alternating series test. Does not converge absolutely by limit comparison with harmonic series.
(Hint: Rationalize the numerator.)
(Hint: Find common denominator then rationalize numerator.)
Converges absolutely by limit comparison with p-series,
after applying the hint.
(Hint: Use Mean Value Theorem.)
Converges by alternating series test since
is decreasing to zero for large
Does not converge absolutely by limit comparison with harmonic series after applying hint.
Converges absolutely, since
are terms of a telescoping series.
Terms do not tend to zero. Series diverges by divergence test.
Converges by alternating series test. Does not converge absolutely by limit comparison with harmonic series.
In each of the following problems, use the estimate
to find a value of
that guarantees that the sum of the first
terms of the alternating series
differs from the infinite sum by at most the given error. Calculate the partial sum
for this
[T]
error
[T]
error
[T]
error
[T]
error
or
or
[T]
error
[T]
error
or
For the following exercises, indicate whether each of the following statements is true or false. If the statement is false, provide an example in which it is false.
If
is decreasing and
then
converges absolutely.
If
is decreasing, then
converges absolutely.
True.
need not tend to zero since if
then
If
and
then
converges.
If
is decreasing and
converges then
converges.
True.
so convergence of
follows from the comparison test.
If
is decreasing and
converges conditionally but not absolutely, then
does not tend to zero.
Let
if
and
if
(Also,
and
If
converges conditionally but not absolutely, then neither
nor
converge.
True. If one converges, then so must the other, implying absolute convergence.
Suppose that
is a sequence of positive real numbers and that
converges.
Suppose that
is an arbitrary sequence of ones and minus ones. Does
necessarily converge?
Suppose that
is a sequence such that
converges for every possible sequence
of zeros and ones. Does
converge absolutely?
Yes. Take
if
and
if
Then
converges. Similarly, one can show
converges. Since both series converge, the series must converge absolutely.
The following series do not satisfy the hypotheses of the alternating series test as stated.
In each case, state which hypothesis is not satisfied. State whether the series converges absolutely.
Not decreasing. Does not converge absolutely.
Not alternating. Can be expressed as
which diverges by comparison with
Show that the alternating series
does
not converge. What hypothesis of the alternating series test is not met?
Suppose that
converges absolutely. Show that the series consisting of the positive terms
also converges.
Let
if
and
if
Then
for all
so the sequence of partial sums of
is increasing and bounded above by the sequence of partial sums of
which converges; hence,
converges.
Show that the alternating series
does not converge. What hypothesis of the alternating series test is not met?
The formula
will be derived in the next chapter. Use the remainder
to find a bound for the error in estimating
by the fifth partial sum
for
and
For
one has
When
When
When
The formula
will be derived in the next chapter. Use the remainder
to find a bound for the error in estimating
by the fifth partial sum
for
and
How many terms in
are needed to approximate
accurate to an error of at most
Let
Then
when
or
and
whereas
How many terms in
are needed to approximate
accurate to an error of at most
Sometimes the alternating series
converges to a certain fraction of an absolutely convergent series
at a faster rate. Given that
find
Which of the series
and
gives a better estimation of
using
terms?
Let
Then
so
The alternating series is more accurate for
terms.
The following alternating series converge to given multiples of
Find the value of
predicted by the remainder estimate such that the
partial sum of the series accurately approximates the left-hand side to within the given error. Find the minimum
for which the error bound holds, and give the desired approximate value in each case. Up to
decimals places,
[T]
error
[T]
error
[T] The series
plays an important role in signal processing. Show that
converges whenever
(Hint: Use the formula for the sine of a sum of angles.)
[T] If
what is
The
partial sum is the same as that for the alternating harmonic series.
[T] Plot the series
for
Explain why
diverges when
How does the series behave for other
[T] Plot the series
for
and comment on its behavior
The series jumps rapidly near the endpoints. For
away from the endpoints, the graph looks like
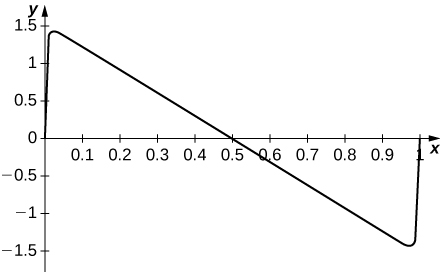
[T] Plot the series
for
and describe its graph.
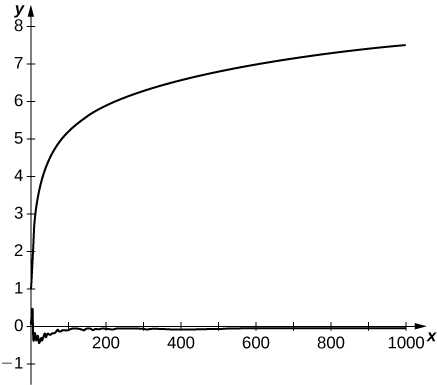
[T] The alternating harmonic series converges because of cancellation among its terms. Its sum is known because the cancellation can be described explicitly. A random harmonic series is one of the form
where
is a randomly generated sequence of
in which the values
are equally likely to occur. Use a random number generator to produce
random
and plot the partial sums
of your random harmonic sequence for
to
Compare to a plot of the first
partial sums of the harmonic series.
Here is a typical result. The top curve consists of partial sums of the harmonic series. The bottom curve plots partial sums of a random harmonic series.* * *
[T] Estimates of
can be accelerated by writing its partial sums as
and recalling that
converges to one as
Compare the estimate of
using the sums
with the estimate using
[T] The Euler transform rewrites
as
For the alternating harmonic series, it takes the form
Compute partial sums of
until they approximate
accurate to within
How many terms are needed? Compare this answer to the number of terms of the alternating harmonic series are needed to estimate
By the alternating series test,
so one needs
terms of the alternating harmonic series to estimate
to within
The first
partial sums of the series
are (up to four decimals)
and the tenth partial sum is within
of
[T] In the text it was stated that a conditionally convergent series can be rearranged to converge to any number. Here is a slightly simpler, but similar, fact. If
is such that
as
but
diverges, then, given any number
there is a sequence
of
such that
Show this for
as follows.
by
if
and
otherwise.
and for any
larger than this
as
converges, the series
is said to converge absolutely
or
where
is called an alternating series
for all integers
and
then an alternating series converges
converges, but the series
diverges, the series
is said to converge conditionally

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: