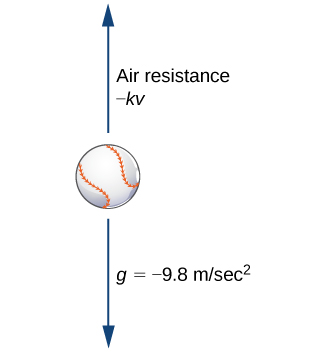
Earlier, we studied an application of a first-order differential equation that involved solving for the velocity of an object. In particular, if a ball is thrown upward with an initial velocity of
ft/s, then an initial-value problem that describes the velocity of the ball after
seconds is given by
This model assumes that the only force acting on the ball is gravity. Now we add to the problem by allowing for the possibility of air resistance acting on the ball.
Air resistance always acts in the direction opposite to motion. Therefore if an object is rising, air resistance acts in a downward direction. If the object is falling, air resistance acts in an upward direction ([link]). There is no exact relationship between the velocity of an object and the air resistance acting on it. For very small objects, air resistance is proportional to velocity; that is, the force due to air resistance is numerically equal to some constant
times
For larger (e.g., baseball-sized) objects, depending on the shape, air resistance can be approximately proportional to the square of the velocity. In fact, air resistance may be proportional to
or
or some other power of

We will work with the linear approximation for air resistance. If we assume
then the expression for the force
due to air resistance is given by
Therefore the sum of the forces acting on the object is equal to the sum of the gravitational force and the force due to air resistance. This, in turn, is equal to the mass of the object multiplied by its acceleration at time
(Newton’s second law). This gives us the differential equation
Finally, we impose an initial condition
where
is the initial velocity measured in meters per second. This makes
The initial-value problem becomes
The differential equation in this initial-value problem is an example of a first-order linear differential equation. (Recall that a differential equation is first-order if the highest-order derivative that appears in the equation is
In this section, we study first-order linear equations and examine a method for finding a general solution to these types of equations, as well as solving initial-value problems involving them.
A first-order differential equation is linear if it can be written in the form
where
and
are arbitrary functions of
Remember that the unknown function
depends on the variable
that is,
is the independent variable and
is the dependent variable. Some examples of first-order linear differential equations are
Examples of first-order nonlinear differential equations include
These equations are nonlinear because of terms like
etc. Due to these terms, it is impossible to put these equations into the same form as [link].
Consider the differential equation
Our main goal in this section is to derive a solution method for equations of this form. It is useful to have the coefficient of
be equal to
To make this happen, we divide both sides by
This is called the standard form of the differential equation. We will use it later when finding the solution to a general first-order linear differential equation. Returning to [link], we can divide both sides of the equation by
This leads to the equation
Now define
and
Then [link] becomes
We can write any first-order linear differential equation in this form, and this is referred to as the standard form for a first-order linear differential equation.
Put each of the following first-order linear differential equations into standard form. Identify
and
for each equation.
(here
to both sides:
In this equation,
and
then subtract
from each side:
Finally, divide both sides by
to make the coefficient of
equal to
This is allowable because in the original statement of this problem we assumed that
(If
then the original equation becomes
which is clearly a false statement.)
In this equation,
and
from each side and add
Next divide both sides by
In this equation,
and
Put the equation
into standard form and identify
and
and
Multiply both sides by the common denominator, then collect all terms involving
on one side.
We now develop a solution technique for any first-order linear differential equation. We start with the standard form of a first-order linear differential equation:
The first term on the left-hand side of [link] is the derivative of the unknown function, and the second term is the product of a known function with the unknown function. This is somewhat reminiscent of the power rule from the Differentiation Rules section. If we multiply [link] by a yet-to-be-determined function
then the equation becomes
The left-hand side [link] can be matched perfectly to the product rule:
Matching term by term gives
and
Taking the derivative of
and setting it equal to the right-hand side of
leads to
This is a first-order, separable differential equation for
We know
because it appears in the differential equation we are solving. Separating variables and integrating yields
Here
can be an arbitrary (positive or negative) constant. This leads to a general method for solving a first-order linear differential equation. We first multiply both sides of [link] by the integrating factor
This gives
The left-hand side of [link] can be rewritten as
Next integrate both sides of [link] with respect to
Divide both sides of [link] by
Since
was previously calculated, we are now finished. An important note about the integrating constant
It may seem that we are inconsistent in the usage of the integrating constant. However, the integral involving
is necessary in order to find an integrating factor for [link]. Only one integrating factor is needed in order to solve the equation; therefore, it is safe to assign a value for
for this integral. We chose
When calculating the integral inside the brackets in [link], it is necessary to keep our options open for the value of the integrating constant, because our goal is to find a general family of solutions to [link]. This integrating factor guarantees just that.
and
and divide both sides by
Find a general solution for the differential equation
Assume
Therefore
and
gives us
You may have noticed the condition that was imposed on the differential equation; namely,
For any nonzero value of
the general solution is not defined at
Furthermore, when
the integrating factor changes. The integrating factor is given by [link] as
For this
we get
since
The behavior of the general solution changes at
largely due to the fact that
is not defined there.
Find the general solution to the differential equation
Assume
Use the method outlined in the problem-solving strategy for first-order linear differential equations.
Now we use the same strategy to find the solution to an initial-value problem.
Solve the initial-value problem
and
gives
Integrate both sides of the equation:
and
into the general solution and solve for
Therefore the solution to the initial-value problem is
Solve the initial-value problem
We look at two different applications of first-order linear differential equations. The first involves air resistance as it relates to objects that are rising or falling; the second involves an electrical circuit. Other applications are numerous, but most are solved in a similar fashion.
We discussed air resistance at the beginning of this section. The next example shows how to apply this concept for a ball in vertical motion. Other factors can affect the force of air resistance, such as the size and shape of the object, but we ignore them here.
A racquetball is hit straight upward with an initial velocity of
m/s. The mass of a racquetball is approximately
kg. Air resistance acts on the ball with a force numerically equal to
where
represents the velocity of the ball at time
meter, how high will it reach?
and
The initial velocity is
m/s. Therefore the initial-value problem is
Dividing the differential equation by
gives
The differential equation is linear. Using the problem-solving strategy for linear differential equations:
Step 1. Rewrite the differential equation as
This gives
and
Step 2. The integrating factor is
Step 3. Multiply the differential equation by
Step 4. Integrate both sides:
Step 5. Solve for
using the initial condition
Therefore the solution to the initial-value problem is
Therefore it takes approximately
second to reach maximum height.
represents the height at time
then
Because we know
and the initial height, we can form an initial-value problem:
Integrating both sides of the differential equation with respect to
gives
Solve for
by using the initial condition:
Therefore
After
second, the height is given by
meter.
The weight of a penny is
grams (United States Mint, “Coin Specifications,” accessed April 9, 2015, http://www.usmint.gov/about_the_mint/?action=coin_specifications), and the upper observation deck of the Empire State Building is
meters above the street. Since the penny is a small and relatively smooth object, air resistance acting on the penny is actually quite small. We assume the air resistance is numerically equal to
Furthermore, the penny is dropped with no initial velocity imparted to it.
approaches infinity)?
Set up the differential equation the same way as [link]. Remember to convert from grams to kilograms.
A source of electromotive force (e.g., a battery or generator) produces a flow of current in a closed circuit, and this current produces a voltage drop across each resistor, inductor, and capacitor in the circuit. Kirchhoff’s Loop Rule states that the sum of the voltage drops across resistors, inductors, and capacitors is equal to the total electromotive force in a closed circuit. We have the following three results:
where
is a constant of proportionality called the resistance, and
is the current.
where
is a constant of proportionality called the inductance, and
again denotes the current.
where
is a constant of proportionality called the capacitance, and
is the instantaneous charge on the capacitor. The relationship between
and
is
We use units of volts
to measure voltage
amperes
to measure current
coulombs
to measure charge
ohms
to measure resistance
henrys
to measure inductance
and farads
to measure capacitance
Consider the circuit in [link].
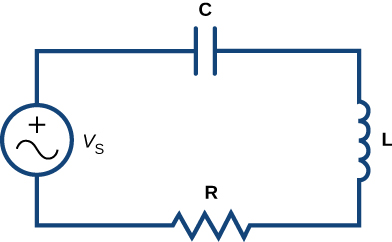
Applying Kirchhoff’s Loop Rule to this circuit, we let
denote the electromotive force supplied by the voltage generator. Then
Substituting the expressions for
and
into this equation, we obtain
If there is no capacitor in the circuit, then the equation becomes
This is a first-order differential equation in
The circuit is referred to as an
circuit.
Next, suppose there is no inductor in the circuit, but there is a capacitor and a resistor, so
and
Then [link] can be rewritten as
which is a first-order linear differential equation. This is referred to as an RC circuit. In either case, we can set up and solve an initial-value problem.
A circuit has in series an electromotive force given by
a resistor of
and an inductor of
If the initial current is
find the current at time
We have a resistor and an inductor in the circuit, so we use [link]. The voltage drop across the resistor is given by
The voltage drop across the inductor is given by
The electromotive force becomes the right-hand side of [link]. Therefore [link] becomes
Dividing both sides by
gives the equation
Since the initial current is 0, this result gives an initial condition of
We can solve this initial-value problem using the five-step strategy for solving first-order differential equations.
Step 1. Rewrite the differential equation as
This gives
and
Step 2. The integrating factor is
Step 3. Multiply the differential equation by
Step 4. Integrate both sides:
Step 5. Solve for
using the initial condition
Therefore the solution to the initial-value problem is
The first term can be rewritten as a single cosine function. First, multiply and divide by
Next, define
to be an acute angle such that
Then
and
Therefore the solution can be written as
The second term is called the attenuation term, because it disappears rapidly as t grows larger. The phase shift is given by
and the amplitude of the steady-state current is given by
The graph of this solution appears in [link]:
![A graph of the given solution over [0, 6] on the x axis. It is an oscillating function, rapidly going from just below -5 to just above 5.](../resources/CNX_Calc_Figure_08_05_004.jpg)
A circuit has in series an electromotive force given by
V, a capacitor with capacitance
and a resistor of
If the initial charge is
find the charge at time
Initial-value problem:
Are the following differential equations linear? Explain your reasoning.
Yes
Yes
Write the following first-order differential equations in standard form.
What are the integrating factors for the following differential equations?
Solve the following differential equations by using integrating factors.
Solve the following differential equations. Use your calculator to draw a family of solutions. Are there certain initial conditions that change the behavior of the solution?
[T]
[T]
[T]
[T]
[T]
[T]
[T]
[T]
Solve the following initial-value problems by using integrating factors.
A falling object of mass
can reach terminal velocity when the drag force is proportional to its velocity, with proportionality constant
Set up the differential equation and solve for the velocity given an initial velocity of
Using your expression from the preceding problem, what is the terminal velocity? (Hint: Examine the limiting behavior; does the velocity approach a value?)
[T] Using your equation for terminal velocity, solve for the distance fallen. How long does it take to fall
meters if the mass is
kilograms, the acceleration due to gravity is
m/s2 and the proportionality constant is
seconds
A more accurate way to describe terminal velocity is that the drag force is proportional to the square of velocity, with a proportionality constant
Set up the differential equation and solve for the velocity.
Using your expression from the preceding problem, what is the terminal velocity? (Hint: Examine the limiting behavior: Does the velocity approach a value?)
[T] Using your equation for terminal velocity, solve for the distance fallen. How long does it take to fall
meters if the mass is
kilograms, the acceleration due to gravity is
and the proportionality constant is
Does it take more or less time than your initial estimate?
For the following problems, determine how parameter
affects the solution.
Solve the generic equation
How does varying
change the behavior?
Solve the generic equation
How does varying
change the behavior?
Solve the generic equation
How does varying
change the behavior?
Solve the generic equation
How does varying
change the behavior?
Solve
with the initial condition
As
approaches
what happens to your formula?
True or False? Justify your answer with a proof or a counterexample.
The differential equation
is linear.
The differential equation
is separable.
F
You can explicitly solve all first-order differential equations by separation or by the method of integrating factors.
You can determine the behavior of all first-order differential equations using directional fields or Euler’s method.
T
For the following problems, find the general solution to the differential equations.
For the following problems, find the solution to the initial value problem.
For the following problems, draw the directional field associated with the differential equation, then solve the differential equation. Draw a sample solution on the directional field.
for
For the following problems, use Euler’s Method with
steps over the interval
Then solve the initial-value problem exactly. How close is your Euler’s Method estimate?
Euler:
exact solution:
For the following problems, set up and solve the differential equations.
A car drives along a freeway, accelerating according to
where
represents time in minutes. Find the velocity at any time
assuming the car starts with an initial speed of
mph.
You throw a ball of mass
kilograms into the air with an upward velocity of
m/s. Find exactly the time the ball will remain in the air, assuming that gravity is given by
second
You drop a ball with a mass of
kilograms out an airplane window at a height of
m. How long does it take for the ball to reach the ground?
You drop the same ball of mass
kilograms out of the same airplane window at the same height, except this time you assume a drag force proportional to the ball’s velocity, using a proportionality constant of
and the ball reaches terminal velocity. Solve for the distance fallen as a function of time. How long does it take the ball to reach the ground?
seconds
A drug is administered to a patient every
hours and is cleared at a rate proportional to the amount of drug left in the body, with proportionality constant
If the patient needs a baseline level of
mg to be in the bloodstream at all times, how large should the dose be?
A
-liter tank contains pure water and a solution of
kg salt/L is pumped into the tank at a rate of
L/min and is drained at the same rate. Solve for total amount of salt in the tank at time
You boil water to make tea. When you pour the water into your teapot, the temperature is
After
minutes in your
room, the temperature of the tea is
Solve the equation to determine the temperatures of the tea at time
How long must you wait until the tea is at a drinkable temperature
The human population (in thousands) of Nevada in
was roughly
If the carrying capacity is estimated at
million individuals, and assuming a growth rate of
per year, develop a logistic growth model and solve for the population in Nevada at any time (use
as time = 0). What population does your model predict for
How close is your prediction to the true value of
Repeat the previous problem but use Gompertz growth model. Which is more accurate?
that is multiplied on both sides of a differential equation to make the side involving the unknown function equal to the derivative of a product of two functions

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: