Separable Equations

Find a general solution to the differential equation $y\prime =\left(x^2-4\right)\left(3y+2\right)$

using the method of separation of variables.

Follow the five-step method of separation of variables.

1. In this example, $f\left(x\right)=x^2-4$

   and

   $g\left(y\right)=3y+2.$

   Setting

   $g(y)=0$

   gives

   $y=-\frac{2}{3}$

   as a constant solution.

2. Rewrite the differential equation in the form

   ---

   $\frac{dy}{3y+2}=(x^2-4)dx.$
3. Integrate both sides of the equation:

   ---

   ${\displaystyle \int \frac{dy}{3y+2}}={\displaystyle \int \left(x^2-4\right)dx}.$

   ---

   Let

   $u=3y+2.$

   Then

   $du=3\frac{dy}{dx}dx,$

   so the equation becomes

   ---

   $\begin{array}{ccc}\hfill \frac{1}{3}{\displaystyle \int \frac{1}{u}du}& =\hfill & \frac{1}{3}{x}^3-4x+C\hfill \\ \hfill \frac{1}{3}\text{ln}\backslash |u\backslash |& =\hfill & \frac{1}{3}{x}^3-4x+C\hfill \\ \hfill \frac{1}{3}\text{ln}\backslash |3y+2\backslash |& =\hfill & \frac{1}{3}{x}^3-4x+C.\hfill \end{array}$
4. To solve this equation for $y,$

   first multiply both sides of the equation by

   $3.$

   ---

   $\text{ln}\backslash |3y+2\backslash |=x^3-12x+3C$

   ---

   Now we use some logic in dealing with the constant

   $C.$

   Since

   $C$

   represents an arbitrary constant,

   $3C$

   also represents an arbitrary constant. If we call the second arbitrary constant

   $C_1,$

   the equation becomes

   ---

   $\text{ln}\backslash |3y+2\backslash |=x^3-12x+C_1.$

   ---

   Now exponentiate both sides of the equation (i.e., make each side of the equation the exponent for the base

   $e).$

   ---

   $\begin{array}{ccc}\hfill e^{\text{ln}\backslash |3y+2\backslash |}& =\hfill & e^{x^3-12x+C_1}\hfill \\ \hfill \backslash |3y+2\backslash |& =\hfill & e^{C_1}{e}^{x^3-12x}\hfill \end{array}$

   ---

   Again define a new constant

   $C_2=e^{c_1}$

   (note that

   $C_2>0)\text{:}$

   ---

   $\backslash |3y+2\backslash |=C_2{e}^{x^3-12x}.$

   ---

   This corresponds to two separate equations:

   $3y+2=C_2{e}^{x^3-12x}$

   and

   $3y+2=\text{−}{C}_2{e}^{x^3-12x}.$

   ---

   The solution to either equation can be written in the form

   $y=\frac{\mathrm{-2}\pm C_2{e}^{x^3-12x}}{3}.$

   ---

   Since

   $C_2>0,$

   it does not matter whether we use plus or minus, so the constant can actually have either sign. Furthermore, the subscript on the constant

   $C$

   is entirely arbitrary, and can be dropped. Therefore the solution can be written as

   ---

   $y=\frac{\mathrm{-2}+C{e}^{x^3-12x}}{3}.$
5. No initial condition is imposed, so we are finished.

Using the method of separation of variables, solve the initial-value problem

Follow the five-step method of separation of variables.

1. In this example, $f(x)=2x+3$

   and

   $g(y)=y^2-4.$

   Setting

   $g(y)=0$

   gives

   $y=\pm 2$

   as constant solutions.

2. Divide both sides of the equation by $y^2-4$

   and multiply by

   $dx.$

   This gives the equation

   ---

   $\frac{dy}{y^2-4}=\left(2x+3\right)dx.$
3. Next integrate both sides:

   ---

   ${\displaystyle \int \frac{1}{y^2-4}dy}={\displaystyle \int \left(2x+3\right)dx}.$

   ---

   To evaluate the left-hand side, use the method of partial fraction decomposition. This leads to the identity

   ---

   $\frac{1}{y^2-4}=\frac{1}{4}\left(\frac{1}{y-2}-\frac{1}{y+2}\right).$

   ---

   Then [link] becomes

   ---

   $\begin{array}{ccc}\hfill \frac{1}{4}{\displaystyle \int \left(\frac{1}{y-2}-\frac{1}{y+2}\right)dy}& =\hfill & {\displaystyle \int \left(2x+3\right)dx}\hfill \\ \hfill \frac{1}{4}\left(\text{ln}\backslash |y-2\backslash |-\text{ln}\backslash |y+2\backslash |\right)& =\hfill & x^2+3x+C.\hfill \end{array}$

   ---

   Multiplying both sides of this equation by

   $4$

   and replacing

   $4C$

   with

   $C_1$

   gives

   ---

   $\begin{array}{ccc}\hfill \text{ln}\backslash |y-2\backslash |-\text{ln}\backslash |y+2\backslash |& =\hfill & 4x^2+12x+C_1\hfill \\ \hfill \text{ln}\backslash |\frac{y-2}{y+2}\backslash |& =\hfill & 4x^2+12x+C_1.\hfill \end{array}$
4. It is possible to solve this equation for y. First exponentiate both sides of the equation and define $C_2=e^{C_1}\text{:}$

   ---

   $\backslash |\frac{y-2}{y+2}\backslash |=C_2{e}^{4x^2+12x}.$

   ---

   Next we can remove the absolute value and let

   $C_2$

   be either positive or negative. Then multiply both sides by

   $y+2.$

   ---

   $\begin{array}{}\\ \\ y-2=C_2\left(y+2\right)e^{4x^2+12x}\hfill \\ y-2=C_{2}y{e}^{{}^{4x^2+12x}}+2C_2{e}^{{}^{4x^2+12x}}.\hfill \end{array}$

   ---

   Now collect all terms involving y on one side of the equation, and solve for

   $y\text{:}$

   ---

   $\begin{array}{ccc}\hfill y-C_{2}y{e}^{4x^2+12x}& =\hfill & 2+2C_2{e}^{4x^2+12x}\hfill \\ \hfill y(1-C_2{e}^{4x^2+12x})& =\hfill & 2+2C_2{e}^{4x^2+12x}\hfill \\ \hfill y& =\hfill & \frac{2+2C_2{e}^{4x^2+12x}}{1-C_2{e}^{4x^2+12x}}.\hfill \end{array}$
5. To determine the value of $C_2,$

   substitute

   $x=0$

   and

   $y=\mathrm{-1}$

   into the general solution. Alternatively, we can put the same values into an earlier equation, namely the equation

   $\frac{y-2}{y+2}=C_2{e}^{4x^2+12}.$

   This is much easier to solve for

   $C_2\text{:}$

   ---

   $\begin{array}{ccc}\hfill \frac{y-2}{y+2}& =\hfill & C_2{e}^{4x^2+12x}\hfill \\ \hfill \frac{\mathrm{-1}-2}{\mathrm{-1}+2}& =\hfill & C_2{e}^{4{\left(0\right)}^2+12\left(0\right)}\hfill \\ \hfill C_2& =\hfill & \mathrm{-3}.\hfill \end{array}$

   ---

   Therefore the solution to the initial-value problem is

   ---

   $y=\frac{2-6e^{4x^2+12x}}{1+3e^{4x^2+12x}}.$

   ---

   A graph of this solution appears in [link].

   ---

   

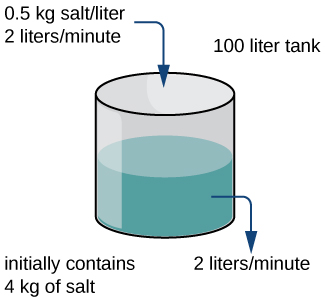
A tank containing $100\text{L}$

of a brine solution initially has $4\text{kg}$

of salt dissolved in the solution. At time $t=0,$

another brine solution flows into the tank at a rate of $2\text{L/min}\text{.}$

This brine solution contains a concentration of $0.5\text{kg/L}$

of salt. At the same time, a stopcock is opened at the bottom of the tank, allowing the combined solution to flow out at a rate of $2\text{L/min},$

so that the level of liquid in the tank remains constant ([link]). Find the amount of salt in the tank as a function of time (measured in minutes), and find the limiting amount of salt in the tank, assuming that the solution in the tank is well mixed at all times.

First we define a function $u(t)$

that represents the amount of salt in kilograms in the tank as a function of time. Then $\frac{du}{dt}$

represents the rate at which the amount of salt in the tank changes as a function of time. Also, $u\left(0\right)$

represents the amount of salt in the tank at time $t=0,$

which is $4$

kilograms.

The general setup for the differential equation we will solve is of the form

INFLOW RATE represents the rate at which salt enters the tank, and OUTFLOW RATE represents the rate at which salt leaves the tank. Because solution enters the tank at a rate of $2$

L/min, and each liter of solution contains $0.5$

kilogram of salt, every minute $2\left(0.5\right)=1\text{kilogram}$

of salt enters the tank. Therefore INFLOW RATE = $1.$

To calculate the rate at which salt leaves the tank, we need the concentration of salt in the tank at any point in time. Since the actual amount of salt varies over time, so does the concentration of salt. However, the volume of the solution remains fixed at 100 liters. The number of kilograms of salt in the tank at time $t$

is equal to $u\left(t\right).$

Thus, the concentration of salt is $\frac{u\left(t\right)}{100}$

kg/L, and the solution leaves the tank at a rate of $2$

L/min. Therefore salt leaves the tank at a rate of $\frac{u\left(t\right)}{100}·2=\frac{u\left(t\right)}{50}$

kg/min, and OUTFLOW RATE is equal to $\frac{u\left(t\right)}{50}.$

Therefore the differential equation becomes $\frac{du}{dt}=1-\frac{u}{50},$

and the initial condition is $u\left(0\right)=4.$

The initial-value problem to be solved is

The differential equation is a separable equation, so we can apply the five-step strategy for solution.

Step 1. Setting $1-\frac{u}{50}=0$

gives $u=50$

as a constant solution. Since the initial amount of salt in the tank is $4$

kilograms, this solution does not apply.

Step 2. Rewrite the equation as

Then multiply both sides by $dt$

and divide both sides by $50-u\text{:}$

Step 3. Integrate both sides:

Step 4. Solve for $u\left(t\right)\text{:}$

Eliminate the absolute value by allowing the constant to be either positive or negative:

Finally, solve for $u\left(t\right)\text{:}$

Step 5. Solve for $C_1\text{:}$

The solution to the initial value problem is $u\left(t\right)=50-46e^{\text{−}t\text{/}50}.$

To find the limiting amount of salt in the tank, take the limit as $t$

approaches infinity:

Note that this was the constant solution to the differential equation. If the initial amount of salt in the tank is $50$

kilograms, then it remains constant. If it starts at less than 50 kilograms, then it approaches 50 kilograms over time.

A pizza is removed from the oven after baking thoroughly, and the temperature of the oven is $350\text{°}\text{F}\text{.}$

The temperature of the kitchen is $75\text{°}\text{F},$

and after $5$

minutes the temperature of the pizza is $340\text{°}\text{F}\text{.}$

We would like to wait until the temperature of the pizza reaches $300\text{°}\text{F}$

before cutting and serving it ([link]). How much longer will we have to wait?

The ambient temperature (surrounding temperature) is $75\text{°}\text{F},$

so $T_s=75.$

The temperature of the pizza when it comes out of the oven is $350\text{°}\text{F},$

which is the initial temperature (i.e., initial value), so $T_0=350.$

Therefore [link] becomes

To solve the differential equation, we use the five-step technique for solving separable equations.

1. Setting the right-hand side equal to zero gives $T=75$

   as a constant solution. Since the pizza starts at

   $350\text{°}\text{F},$

   this is not the solution we are seeking.

2. Rewrite the differential equation by multiplying both sides by $dt$

   and dividing both sides by

   $T-75\text{:}$

   ---

   $\frac{dT}{T-75}=kdt.$
3. Integrate both sides:

   ---

   $\begin{array}{ccc}\hfill {\displaystyle \int \frac{dT}{T-75}}& =\hfill & {\displaystyle \int kdt}\hfill \\ \hfill \text{ln}\backslash |T-75\backslash |& =\hfill & kt+C.\hfill \end{array}$
4. Solve for $T$

   by first exponentiating both sides:

   ---

   $\begin{array}{ccc}\hfill e^{\text{ln}\backslash |T-75\backslash |}& =\hfill & e^{kt+C}\hfill \\ \hfill \backslash |T-75\backslash |& =\hfill & C_1{e}^{kt}\hfill \\ \hfill T-75& =\hfill & C_1{e}^{kt}\hfill \\ \hfill T(t)& =\hfill & 75+C_1{e}^{kt}.\hfill \end{array}$
5. Solve for $C_1$

   by using the initial condition

   $T\left(0\right)=350\text{:}$

   ---

   $\begin{array}{ccc}\hfill T(t)& =\hfill & 75+C_1{e}^{kt}\hfill \\ \hfill T\left(0\right)& =\hfill & 75+C_1{e}^{k\left(0\right)}\hfill \\ \hfill 350& =\hfill & 75+C_1\hfill \\ \hfill C_1& =\hfill & 275.\hfill \end{array}$

   ---

   Therefore the solution to the initial-value problem is

   ---

   $T(t)=75+275e^{kt}.$

   ---

   To determine the value of

   $k,$

   we need to use the fact that after

   $5$

   minutes the temperature of the pizza is

   $340\text{°}\text{F}\text{.}$

   Therefore

   $T\left(5\right)=340.$

   Substituting this information into the solution to the initial-value problem, we have

   ---

   $\begin{array}{ccc}\hfill T(t)& =\hfill & 75+275e^{kt}\hfill \\ \hfill T\left(5\right)& =\hfill & 340=75+275e^{5k}\hfill \\ \hfill 265& =\hfill & 275e^{5k}\hfill \\ \hfill e^{5k}& =\hfill & \frac{53}{55}\hfill \\ \hfill \text{ln}{e}^{5k}& =\hfill & \text{ln}\left(\frac{53}{55}\right)\hfill \\ \hfill 5k& =\hfill & \text{ln}\left(\frac{53}{55}\right)\hfill \\ \hfill k& =\hfill & \frac{1}{5}\text{ln}\left(\frac{53}{55}\right)\approx -\mathrm{0.007408.}\hfill \end{array}$

   ---

   So now we have

   $T(t)=75+275e^{\mathrm{-0.007048}t}.$

   When is the temperature

   $300\text{°}\text{F?}$

   Solving for

   $t,$

   we find

   ---

   $\begin{array}{ccc}\hfill T(t)& =\hfill & 75+275e^{\mathrm{-0.007048}t}\hfill \\ \hfill 300& =\hfill & 75+275e^{\mathrm{-0.007048}t}\hfill \\ \hfill 225& =\hfill & 275e^{\mathrm{-0.007048}t}\hfill \\ \hfill e^{\mathrm{-0.007048}t}& =\hfill & \frac{9}{11}\hfill \\ \hfill \text{ln}{e}^{\mathrm{-0.007048}t}& =\hfill & \text{ln}\frac{9}{11}\hfill \\ \hfill \mathrm{-0.007048}t& =\hfill & \text{ln}\frac{9}{11}\hfill \\ \hfill t& =\hfill & -\frac{1}{0.007048}\text{ln}\frac{9}{11}\approx \mathrm{28.5.}\hfill \end{array}$

   ---

   Therefore we need to wait an additional

   $23.5$

   minutes (after the temperature of the pizza reached

   $340\text{°}\text{F}).$

   That should be just enough time to finish this calculation.