Numerical Integration

The antiderivatives of many functions either cannot be expressed or cannot be expressed easily in closed form (that is, in terms of known functions). Consequently, rather than evaluate definite integrals of these functions directly, we resort to various techniques of numerical integration to approximate their values. In this section we explore several of these techniques. In addition, we examine the process of estimating the error in using these techniques.

The Midpoint Rule

Earlier in this text we defined the definite integral of a function over an interval as the limit of Riemann sums. In general, any Riemann sum of a function f(x)

over an interval [a,b]

may be viewed as an estimate of ∫abf(x)dx.

Recall that a Riemann sum of a function f(x)

over an interval [a,b]

is obtained by selecting a partition

P={x0,x1,x2,…,xn},wherea=x0<x1<x2<⋯<xn=b

and a set

S={x1*,x2*,…,xn*},wherexi−1≤xi*≤xifor alli.

The Riemann sum corresponding to the partition P

and the set S

is given by ∑i=1nf(xi*)Δxi,

where Δxi=xi−xi−1,

the length of the ith subinterval.

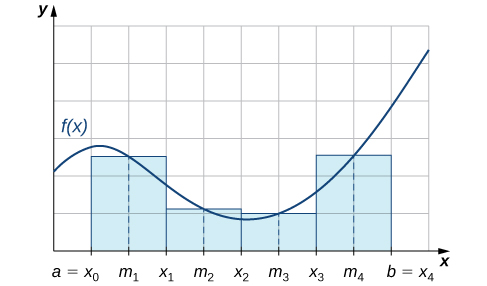
The midpoint rule for estimating a definite integral uses a Riemann sum with subintervals of equal width and the midpoints, mi,

of each subinterval in place of xi*.

Formally, we state a theorem regarding the convergence of the midpoint rule as follows.

The Midpoint Rule

Assume that f(x)

is continuous on [a,b].

Let n be a positive integer and Δx=b−an.

If [a,b]

is divided into n

subintervals, each of length Δx,

and mi

is the midpoint of the ith subinterval, set

Mn=∑i=1nf(mi)Δx.

Then limn→∞Mn=∫abf(x)dx.

As we can see in [link], if f(x)≥0

over [a,b],

then ∑i=1nf(mi)Δx

corresponds to the sum of the areas of rectangles approximating the area between the graph of f(x)

and the x-axis over [a,b].

The graph shows the rectangles corresponding to M4

for a nonnegative function over a closed interval [a,b].

This figure is a graph of a non-negative function in the first quadrant. The function increases and decreases. The quadrant is divided into a grid. Beginning on the x-axis at the point labeled a = x sub 0, there are rectangles shaded whose heights are approximately the height of the curve. The x-axis is scaled by increments of msub1, x sub 1, m sub 2, x sub 2, m sub 3, x sub 3, m sub 4 and b = x sub 4.

Using the Midpoint Rule with M4

Use the midpoint rule to estimate ∫01x2dx

using four subintervals. Compare the result with the actual value of this integral.

Each subinterval has length Δx=1−04=14.

Therefore, the subintervals consist of

[0,14],[14,12],[12,34],and[34,1].

The midpoints of these subintervals are {18,38,58,78}.

Thus,

M4=14f(18)+14f(38)+14f(58)+14f(78)=14·164+14·964+14·2564+14·2164=2164.

Since

∫01x2dx=13and\|13−2164\|=1192≈0.0052,

we see that the midpoint rule produces an estimate that is somewhat close to the actual value of the definite integral.

Using the Midpoint Rule with M6

Use M6

to estimate the length of the curve y=12x2

on [1,4].

The length of y=12x2

on [1,4]

is

∫141+(dydx)2dx.

Since dydx=x,

this integral becomes ∫141+x2dx.

If [1,4]

is divided into six subintervals, then each subinterval has length Δx=4−16=12

and the midpoints of the subintervals are {54,74,94,114,134,154}.

If we set f(x)=1+x2,

M6=12f(54)+12f(74)+12f(94)+12f(114)+12f(134)+12f(154)≈12(1.6008+2.0156+2.4622+2.9262+3.4004+3.8810)=8.1431.

Use the midpoint rule with n=2

to estimate ∫121xdx.

2435
Hint
Δx=12, m1=54,

and m2=74.

The Trapezoidal Rule

We can also approximate the value of a definite integral by using trapezoids rather than rectangles. In [link], the area beneath the curve is approximated by trapezoids rather than by rectangles.

This figure is a graph of a non-negative function in the first quadrant. The function increases and decreases. The quadrant is divided into a grid. Beginning on the x-axis at the point labeled a = x sub 0, there are trapezoids shaded whose heights are approximately the height of the curve. The x-axis is scaled by increments of a = x sub 0, x sub 1, x sub 2, x sub 3, and b = x sub 4.

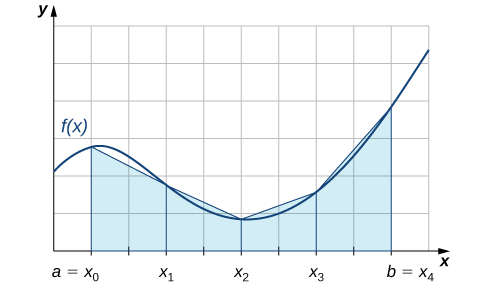
The trapezoidal rule for estimating definite integrals uses trapezoids rather than rectangles to approximate the area under a curve. To gain insight into the final form of the rule, consider the trapezoids shown in [link]. We assume that the length of each subinterval is given by Δx.

First, recall that the area of a trapezoid with a height of h and bases of length b1

and b2

is given by Area=12h(b1+b2).

We see that the first trapezoid has a height Δx

and parallel bases of length f(x0)

and f(x1).

Thus, the area of the first trapezoid in [link] is

12Δx(f(x0)+f(x1)).

The areas of the remaining three trapezoids are

12Δx(f(x1)+f(x2)),12Δx(f(x2)+f(x3)),and12Δx(f(x3)+f(x4)).

Consequently,

∫abf(x)dx≈12Δx(f(x0)+f(x1))+12Δx(f(x1)+f(x2))+12Δx(f(x2)+f(x3))+12Δx(f(x3)+f(x4)).

After taking out a common factor of 12Δx

and combining like terms, we have

∫abf(x)dx≈12Δx(f(x0)+2f(x1)+2f(x2)+2f(x3)+f(x4)).

Generalizing, we formally state the following rule.

The Trapezoidal Rule

Assume that f(x)

is continuous over [a,b].

Let n be a positive integer and Δx=b−an.

Let [a,b]

be divided into n

subintervals, each of length Δx,

with endpoints at P={x0,x1,x2…,xn}.

Set

Tn=12Δx(f(x0)+2f(x1)+2f(x2)+⋯+2f(xn−1)+f(xn)).

Then, limn→+∞Tn=∫abf(x)dx.

Before continuing, let’s make a few observations about the trapezoidal rule. First of all, it is useful to note that

Tn=12(Ln+Rn)whereLn=∑i=1nf(xi−1)ΔxandRn=∑i=1nf(xi)Δx.

That is, Ln

and Rn

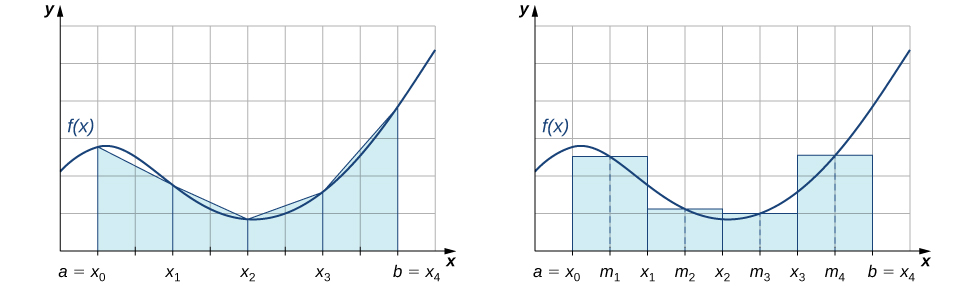
approximate the integral using the left-hand and right-hand endpoints of each subinterval, respectively. In addition, a careful examination of [link] leads us to make the following observations about using the trapezoidal rules and midpoint rules to estimate the definite integral of a nonnegative function. The trapezoidal rule tends to overestimate the value of a definite integral systematically over intervals where the function is concave up and to underestimate the value of a definite integral systematically over intervals where the function is concave down. On the other hand, the midpoint rule tends to average out these errors somewhat by partially overestimating and partially underestimating the value of the definite integral over these same types of intervals. This leads us to hypothesize that, in general, the midpoint rule tends to be more accurate than the trapezoidal rule.

This figure has two graphs, both of the same non-negative function in the first quadrant. The function increases and decreases. The quadrant is divided into a grid. The first graph, beginning on the x-axis at the point labeled a = x sub 0, there are trapezoids shaded whose heights are approximately the height of the curve. The x-axis is scaled by increments of a = x sub 0, xsub1, x sub 2, x sub 3, and b = x sub 4. The second graph has on the x-axis at the point labeled a = x sub 0. There are rectangles shaded whose heights are approximately the height of the curve. The x-axis is scaled by increments of m sub 1, x sub 1, m sub 2, x sub 2, m sub 3, x sub 3, m sub 4 and b = x sub 4.

Using the Trapezoidal Rule

Use the trapezoidal rule to estimate ∫01x2dx

using four subintervals.

The endpoints of the subintervals consist of elements of the set P={0,14,12,34,1}

and Δx=1−04=14.

Thus,

∫01x2dx≈12·14(f(0)+2f(14)+2f(12)+2f(34)+f(1))=18(0+2·116+2·14+2·916+1)=1132.

Use the trapezoidal rule with n=2

to estimate ∫121xdx.

1724
Hint

Set Δx=12.

The endpoints of the subintervals are the elements of the set P={1,32,2}.

Absolute and Relative Error

An important aspect of using these numerical approximation rules consists of calculating the error in using them for estimating the value of a definite integral. We first need to define absolute error and relative error.

Definition

If B

is our estimate of some quantity having an actual value of A,

then the absolute error is given by \|A−B\|.

The relative error is the error as a percentage of the absolute value and is given by \|A−BA\|=\|A−BA\|·100%.

Calculating Error in the Midpoint Rule

Calculate the absolute and relative error in the estimate of ∫01x2dx

using the midpoint rule, found in [link].

The calculated value is ∫01x2dx=13

and our estimate from the example is M4=2164.

Thus, the absolute error is given by \|(13)−(2164)\|=1192≈0.0052.

The relative error is

1/1921/3=164≈0.015625≈1.6%.
Calculating Error in the Trapezoidal Rule

Calculate the absolute and relative error in the estimate of ∫01x2dx

using the trapezoidal rule, found in [link].

The calculated value is ∫01x2dx=13

and our estimate from the example is T4=1132.

Thus, the absolute error is given by \|13−1132\|=196≈0.0104.

The relative error is given by

1/961/3=0.03125≈3.1%.

In an earlier checkpoint, we estimated ∫121xdx

to be 2435

using T2.

The actual value of this integral is ln2.

Using 2435≈0.6857

and ln2≈0.6931,

calculate the absolute error and the relative error.

0.0074, 1.1%

Hint

Use the previous examples as a guide.

In the two previous examples, we were able to compare our estimate of an integral with the actual value of the integral; however, we do not typically have this luxury. In general, if we are approximating an integral, we are doing so because we cannot compute the exact value of the integral itself easily. Therefore, it is often helpful to be able to determine an upper bound for the error in an approximation of an integral. The following theorem provides error bounds for the midpoint and trapezoidal rules. The theorem is stated without proof.

Error Bounds for the Midpoint and Trapezoidal Rules

Let f(x)

be a continuous function over [a,b],

having a second derivative f″(x)

over this interval. If M

is the maximum value of \|f″(x)\|

over [a,b],

then the upper bounds for the error in using Mn

and Tn

to estimate ∫abf(x)dx

are

Error inMn≤M(b−a)324n2

and

Error inTn≤M(b−a)312n2.

We can use these bounds to determine the value of n

necessary to guarantee that the error in an estimate is less than a specified value.

Determining the Number of Intervals to Use

What value of n

should be used to guarantee that an estimate of ∫01ex2dx

is accurate to within 0.01 if we use the midpoint rule?

We begin by determining the value of M,

the maximum value of \|f″(x)\|

over [0,1]

for f(x)=ex2.

Since f′(x)=2xex2,

we have

f″(x)=2ex2+4x2ex2.

Thus,

\|f″(x)\|=2ex2(1+2x2)≤2·e·3=6e.

From the error-bound [link], we have

Error inMn≤M(b−a)324n2≤6e(1−0)324n2=6e24n2.

Now we solve the following inequality for n:

6e24n2≤0.01.

Thus, n≥600e24≈8.24.

Since n

must be an integer satisfying this inequality, a choice of n=9

would guarantee that \|∫01ex2dx−Mn\|<0.01.

Analysis

We might have been tempted to round 8.24

down and choose n=8,

but this would be incorrect because we must have an integer greater than or equal to 8.24.

We need to keep in mind that the error estimates provide an upper bound only for the error. The actual estimate may, in fact, be a much better approximation than is indicated by the error bound.

Use [link] to find an upper bound for the error in using M4

to estimate ∫01x2dx.

1192
Hint
f″(x)=2,

so M=2.

Simpson’s Rule

With the midpoint rule, we estimated areas of regions under curves by using rectangles. In a sense, we approximated the curve with piecewise constant functions. With the trapezoidal rule, we approximated the curve by using piecewise linear functions. What if we were, instead, to approximate a curve using piecewise quadratic functions? With Simpson’s rule, we do just this. We partition the interval into an even number of subintervals, each of equal width. Over the first pair of subintervals we approximate ∫x0x2f(x)dx

with ∫x0x2p(x)dx,

where p(x)=Ax2+Bx+C

is the quadratic function passing through (x0,f(x0)),

(x1,f(x1)),

and (x2,f(x2))

([link]). Over the next pair of subintervals we approximate ∫x2x4f(x)dx

with the integral of another quadratic function passing through (x2,f(x2)),

(x3,f(x3)),

and (x4,f(x4)).

This process is continued with each successive pair of subintervals.

This figure has two graphs, both of the same non-negative function in the first quadrant. The function increases and decreases. The quadrant is divided into a grid. The first graph, beginning on the x-axis at the point labeled x sub 0, there are trapezoids shaded whose heights are represented by the function p(x), which is a curve following an approximate path of the original graph. The x-axis is scaled by increments of x sub 0, x sub 1, x sub 2. The second graph has on the x-axis at the point labeled x sub 0. There are shaded regions under the curve, divided by x sub 0, x sub 1, x sub 2, x sub 3, and x sub 4. The curve is sectioned into two different parts above the shaded areas. These two parts are labeled p sub 1(x) and p sub 2(x).

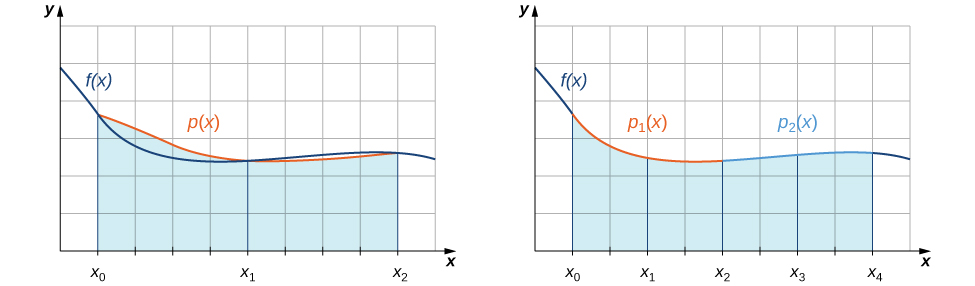
To understand the formula that we obtain for Simpson’s rule, we begin by deriving a formula for this approximation over the first two subintervals. As we go through the derivation, we need to keep in mind the following relationships:

f(x0)=p(x0)=Ax02+Bx0+Cf(x1)=p(x1)=Ax12+Bx1+Cf(x2)=p(x2)=Ax22+Bx2+C
x2−x0=2Δx,

where Δx

is the length of a subinterval.

x2+x0=2x1,sincex1=(x2+x0)2.

Thus,

∫x0x2f(x)dx≈∫x0x2p(x)dx=∫x0x2(Ax2+Bx+C)dx=A3x3+B2x2+Cx\|x2x0Find the antiderivative.=A3(x23−x03)+B2(x22−x02)+C(x2−x0)Evaluate the antiderivative.=A3(x2−x0)(x22+x2x0+x02)+B2(x2−x0)(x2+x0)+C(x2−x0)=x2−x06(2A(x22+x2x0+x02)+3B(x2+x0)+6C)Factor outx2−x06.=Δx3((Ax22+Bx2+C)+(Ax02+Bx0+C)+A(x22+2x2x0+x02)+2B(x2+x0)+4C)=Δx3(f(x2)+f(x0)+A(x2+x0)2+2B(x2+x0)+4C)Rearrange the terms.Factor and substitute.f(x2)=Ax02+Bx0+Candf(x0)=Ax02+Bx0+C.=Δx3(f(x2)+f(x0)+A(2x1)2+2B(2x1)+4C)Substitutex2+x0=2x1.=Δx3(f(x2)+4f(x1)+f(x0)).Expand and substitutef(x1)=Ax12+Bx1+.

If we approximate ∫x2x4f(x)dx

using the same method, we see that we have

∫x0x4f(x)dx≈Δx3(f(x4)+4f(x3)+f(x2)).

Combining these two approximations, we get

∫x0x4f(x)dx=Δx3(f(x0)+4f(x1)+2f(x2)+4f(x3)+f(x4)).

The pattern continues as we add pairs of subintervals to our approximation. The general rule may be stated as follows.

Simpson’s Rule

Assume that f(x)

is continuous over [a,b].

Let n be a positive even integer and Δx=b−an.

Let [a,b]

be divided into n

subintervals, each of length Δx,

with endpoints at P={x0,x1,x2,…,xn}.

Set

Sn=Δx3(f(x0)+4f(x1)+2f(x2)+4f(x3)+2f(x4)+⋯+2f(xn−2)+4f(xn−1)+f(xn)).

Then,

limn→+∞Sn=∫abf(x)dx.

Just as the trapezoidal rule is the average of the left-hand and right-hand rules for estimating definite integrals, Simpson’s rule may be obtained from the midpoint and trapezoidal rules by using a weighted average. It can be shown that S2n=(23)Mn+(13)Tn.

It is also possible to put a bound on the error when using Simpson’s rule to approximate a definite integral. The bound in the error is given by the following rule:

Rule: Error Bound for Simpson’s Rule

Let f(x)

be a continuous function over [a,b]

having a fourth derivative, f(4)(x),

over this interval. If M

is the maximum value of \|f(4)(x)\|

over [a,b],

then the upper bound for the error in using Sn

to estimate ∫abf(x)dx

is given by

Error inSn≤M(b−a)5180n4.
Applying Simpson’s Rule 1

Use S2

to approximate ∫01x3dx.

Estimate a bound for the error in S2.

Since [0,1]

is divided into two intervals, each subinterval has length Δx=1−02=12.

The endpoints of these subintervals are {0,12,1}.

If we set f(x)=x3,

then

S4=13·12(f(0)+4f(12)+f(1))=16(0+4·18+1)=14.

Since f(4)(x)=0

and consequently M=0,

we see that

Error inS2≤0(1)5180⋅24=0.

This bound indicates that the value obtained through Simpson’s rule is exact. A quick check will verify that, in fact, ∫01x3dx=14.

Applying Simpson’s Rule 2

Use S6

to estimate the length of the curve y=12x2

over [1,4].

The length of y=12x2

over [1,4]

is ∫141+x2dx.

If we divide [1,4]

into six subintervals, then each subinterval has length Δx=4−16=12,

and the endpoints of the subintervals are {1,32,2,52,3,72,4}.

Setting f(x)=1+x2,

S6=13·12(f(1)+4f(32)+2f(2)+4f(52)+2f(3)+4f(72)+f(4)).

After substituting, we have

S6=16(1.4142+4·1.80278+2·2.23607+4·2.69258+2·3.16228+4·3.64005+4.12311)≈8.14594.

Use S2

to estimate ∫121xdx.

2536
Hint
S2=(13Δx(f(x0)+4f(x1)+f(x2))

Key Concepts

Key Equations

Approximate the following integrals using either the midpoint rule, trapezoidal rule, or Simpson’s rule as indicated. (Round answers to three decimal places.)

∫12dxx;

trapezoidal rule; n=5

0.696

∫034+x3dx;

trapezoidal rule; n=6

∫034+x3dx;

Simpson’s rule; n=3

9.279

∫012x2dx;

midpoint rule; n=6

∫01sin2(πx)dx;

midpoint rule; n=3

0.5000

Use the midpoint rule with eight subdivisions to estimate ∫24x2dx.

Use the trapezoidal rule with four subdivisions to estimate ∫24x2dx.

T4=18.75

Find the exact value of ∫24x2dx.

Find the error of approximation between the exact value and the value calculated using the trapezoidal rule with four subdivisions. Draw a graph to illustrate.

Approximate the integral to three decimal places using the indicated rule.

∫01sin2(πx)dx;

trapezoidal rule; n=6

0.500

∫0311+x3dx;

trapezoidal rule; n=6

∫0311+x3dx;

Simpson’s rule; n=3

1.1614

∫00.8e−x2dx;

trapezoidal rule; n=4

∫00.8e−x2dx;

Simpson’s rule; n=4

0.6577

∫00.4sin(x2)dx;

trapezoidal rule; n=4

∫00.4sin(x2)dx;

Simpson’s rule; n=4

0.0213

∫0.10.5cosxxdx;

trapezoidal rule; n=4

∫0.10.5cosxxdx;

Simpson’s rule; n=4

1.5629

Evaluate ∫01dx1+x2

exactly and show that the result is π/4.

Then, find the approximate value of the integral using the trapezoidal rule with n=4

subdivisions. Use the result to approximate the value of π.

Approximate ∫241lnxdx

using the midpoint rule with four subdivisions to four decimal places.

1.9133

Approximate ∫241lnxdx

using the trapezoidal rule with eight subdivisions to four decimal places.

Use the trapezoidal rule with four subdivisions to estimate ∫00.8x3dx

to four decimal places.

T(4)=0.1088

Use the trapezoidal rule with four subdivisions to estimate ∫00.8x3dx.

Compare this value with the exact value and find the error estimate.

Using Simpson’s rule with four subdivisions, find ∫0π/2cos(x)dx.

1.0

Show that the exact value of ∫01xe−xdx=1−2e.

Find the absolute error if you approximate the integral using the midpoint rule with 16 subdivisions.

Given ∫01xe−xdx=1−2e,

use the trapezoidal rule with 16 subdivisions to approximate the integral and find the absolute error.

Approximate error is 0.000325.

Find an upper bound for the error in estimating ∫03(5x+4)dx

using the trapezoidal rule with six steps.

Find an upper bound for the error in estimating ∫451(x−1)2dx

using the trapezoidal rule with seven subdivisions.

17938

Find an upper bound for the error in estimating ∫03(6x2−1)dx

using Simpson’s rule with n=10

steps.

Find an upper bound for the error in estimating ∫251x−1dx

using Simpson’s rule with n=10

steps.

8125,000

Find an upper bound for the error in estimating ∫0π2xcos(x)dx

using Simpson’s rule with four steps.

Estimate the minimum number of subintervals needed to approximate the integral ∫14(5x2+8)dx

with an error magnitude of less than 0.0001 using the trapezoidal rule.

475

Determine a value of n such that the trapezoidal rule will approximate ∫011+x2dx

with an error of no more than 0.01.

Estimate the minimum number of subintervals needed to approximate the integral ∫23(2x3+4x)dx

with an error of magnitude less than 0.0001 using the trapezoidal rule.

174

Estimate the minimum number of subintervals needed to approximate the integral ∫341(x−1)2dx

with an error magnitude of less than 0.0001 using the trapezoidal rule.

Use Simpson’s rule with four subdivisions to approximate the area under the probability density function y=12πe−x2/2

from x=0

to x=0.4.

0.1544

Use Simpson’s rule with n=14

to approximate (to three decimal places) the area of the region bounded by the graphs of y=0,

x=0,

and x=π/2.

The length of one arch of the curve y=3sin(2x)

is given by L=∫0π/21+36cos2(2x)dx.

Estimate L using the trapezoidal rule with n=6.

6.2807

The length of the ellipse x=acos(t),y=bsin(t),0≤t≤2π

is given by L=4a∫0π/21−e2cos2(t)dt,

where e is the eccentricity of the ellipse. Use Simpson’s rule with n=6

subdivisions to estimate the length of the ellipse when a=2

and e=1/3.

Estimate the area of the surface generated by revolving the curve y=cos(2x),0≤x≤π4

about the x-axis. Use the trapezoidal rule with six subdivisions.

4.606

Estimate the area of the surface generated by revolving the curve y=2x2,

0≤x≤3

about the x-axis. Use Simpson’s rule with n=6.

The growth rate of a certain tree (in feet) is given by y=2t+1+e−t2/2,

where t is time in years. Estimate the growth of the tree through the end of the second year by using Simpson’s rule, using two subintervals. (Round the answer to the nearest hundredth.)

3.41 ft

[T] Use a calculator to approximate ∫01sin(πx)dx

using the midpoint rule with 25 subdivisions. Compute the relative error of approximation.

[T] Given ∫15(3x2−2x)dx=100,

approximate the value of this integral using the midpoint rule with 16 subdivisions and determine the absolute error.

T16=100.125;

absolute error = 0.125

Given that we know the Fundamental Theorem of Calculus, why would we want to develop numerical methods for definite integrals?

The table represents the coordinates (x,​y)

that give the boundary of a lot. The units of measurement are meters. Use the trapezoidal rule to estimate the number of square meters of land that is in this lot.

| x | y | x | y | {: valign=”top”}|———- | 0 | 125 | 600 | 95 | {: valign=”top”}| 100 | 125 | 700 | 88 | {: valign=”top”}| 200 | 120 | 800 | 75 | {: valign=”top”}| 300 | 112 | 900 | 35 | {: valign=”top”}| 400 | 90 | 1000 | 0 | {: valign=”top”}| 500 | 90 | | | {: valign=”top”}{: .unnumbered summary=”This is a table with four columns and seven rows. The first row is a header row and is labeled “x,” “y,” “x,” “y.” The entries under the first column are 0, 100, 200, 300, 400, and 500. The entries in the second column are 125, 125, 120, 112, 90, and 90. The entries in the third column are 600, 700, 800, 900, 1000, and blank. The entries in the fourth column are 95, 88, 75, 35, 0, and blank.”}

about 89,250 m2

Choose the correct answer. When Simpson’s rule is used to approximate the definite integral, it is necessary that the number of partitions be____

  1. an even number
  2. odd number
  3. either an even or an odd number
  4. a multiple of 4

The “Simpson” sum is based on the area under a ____.

parabola

The error formula for Simpson’s rule depends on___.

  1. f(x)
  2. f′(x)
  3. f(4)(x)
  4. the number of steps

Glossary

absolute error
if B

is an estimate of some quantity having an actual value of

A,

then the absolute error is given by

\|A−B\|
midpoint rule
a rule that uses a Riemann sum of the form Mn=∑i=1nf(mi)Δx,

where

mi

is the midpoint of the ith subinterval to approximate

∫abf(x)dx
numerical integration
the variety of numerical methods used to estimate the value of a definite integral, including the midpoint rule, trapezoidal rule, and Simpson’s rule
relative error
error as a percentage of the absolute value, given by \|A−BA\|=\|A−BA\|·100%
Simpson’s rule
a rule that approximates ∫abf(x)dx

using the integrals of a piecewise quadratic function. The approximation

Sn

to

∫abf(x)dx

is given by

Sn=Δx3(f(x0)+4f(x1)+2f(x2)+4f(x3)+2f(x4)+4f(x5)+⋯+2f(xn−2)+4f(xn−1)+f(xn))

trapezoidal rule a rule that approximates

∫abf(x)dx

using trapezoids

Creative Commons License
This work is licensed under a Creative Commons Attribution 4.0 International License.

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1

Attribution: