Other Strategies for Integration
- Use a table of integrals to solve integration problems.
- Use a computer algebra system (CAS) to solve integration problems.
In addition to the techniques of integration we have already seen, several other tools are widely available to assist with the process of integration. Among these tools are integration tables, which are readily available in many books, including the appendices to this one. Also widely available are computer algebra systems (CAS), which are found on calculators and in many campus computer labs, and are free online.
Tables of Integrals
Integration tables, if used in the right manner, can be a handy way either to evaluate or check an integral quickly. Keep in mind that when using a table to check an answer, it is possible for two completely correct solutions to look very different. For example, in Trigonometric Substitution, we found that, by using the substitution
we can arrive at
However, using
we obtained a different solution—namely,
We later showed algebraically that the two solutions are equivalent. That is, we showed that
In this case, the two antiderivatives that we found were actually equal. This need not be the case. However, as long as the difference in the two antiderivatives is a constant, they are equivalent.
Using a Formula from a Table to Evaluate an Integral
Use the table formula
to evaluate
If we look at integration tables, we see that several formulas contain expressions of the form
This expression is actually similar to
where
and
Keep in mind that we must also have
Multiplying the numerator and the denominator of the given integral by
should help to put this integral in a useful form. Thus, we now have
Substituting
and
produces
From the integration table (#88 in Appendix A),
Thus,
Computer Algebra Systems
If available, a CAS is a faster alternative to a table for solving an integration problem. Many such systems are widely available and are, in general, quite easy to use.
Using a Computer Algebra System to Evaluate an Integral
Use a computer algebra system to evaluate
Compare this result with
a result we might have obtained if we had used trigonometric substitution.
Using Wolfram Alpha, we obtain
Notice that
Since these two antiderivatives differ by only a constant, the solutions are equivalent. We could have also demonstrated that each of these antiderivatives is correct by differentiating them.
Using a CAS to Evaluate an Integral
Evaluate
using a CAS. Compare the result to
the result we might have obtained using the technique for integrating odd powers of
discussed earlier in this chapter.
Using Wolfram Alpha, we obtain
This looks quite different from
To see that these antiderivatives are equivalent, we can make use of a few trigonometric identities:
Thus, the two antiderivatives are identical.
We may also use a CAS to compare the graphs of the two functions, as shown in the following figure.
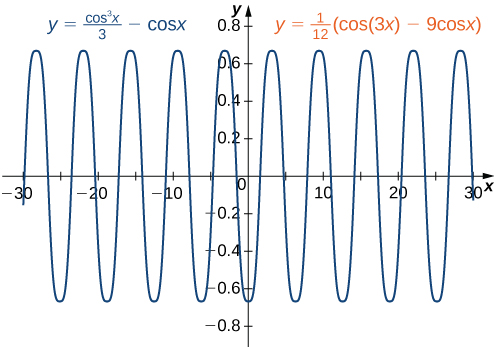
Use a CAS to evaluate
Possible solutions include
and
Key Concepts
- An integration table may be used to evaluate indefinite integrals.
- A CAS (or computer algebra system) may be used to evaluate indefinite integrals.
- It may require some effort to reconcile equivalent solutions obtained using different methods.
Use a table of integrals to evaluate the following integrals.
Use a CAS to evaluate the following integrals. Tables can also be used to verify the answers.
Use a calculator or CAS to evaluate the following integrals.
Use tables to evaluate the integrals. You may need to complete the square or change variables to put the integral into a form given in the table.
Use tables to perform the integration.
Find the area bounded by
Use a table of integrals or a CAS.
The region bounded between the curve
and the x-axis is revolved about the x-axis to generate a solid. Use a table of integrals to find the volume of the solid generated. (Round the answer to two decimal places.)
Use substitution and a table of integrals to find the area of the surface generated by revolving the curve
about the x-axis. (Round the answer to two decimal places.)
[T] Use an integral table and a calculator to find the area of the surface generated by revolving the curve
about the x-axis. (Round the answer to two decimal places.)
[T] Use a CAS or tables to find the area of the surface generated by revolving the curve
about the x-axis. (Round the answer to two decimal places.)
Find the length of the curve
over
Find the length of the curve
over
Find the area of the surface formed by revolving the graph of
over the interval
about the x-axis.
Find the average value of the function
over the interval
Approximate the arc length of the curve
over the interval
(Round the answer to three decimal places.)
Glossary
- computer algebra system (CAS)
- technology used to perform many mathematical tasks, including integration
- integration table
- a table that lists integration formulas

This work is licensed under a Creative Commons Attribution 4.0 International License.
You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution:

