We were introduced to hyperbolic functions in Introduction to Functions and Graphs, along with some of their basic properties. In this section, we look at differentiation and integration formulas for the hyperbolic functions and their inverses.
Recall that the hyperbolic sine and hyperbolic cosine are defined as
The other hyperbolic functions are then defined in terms of
and
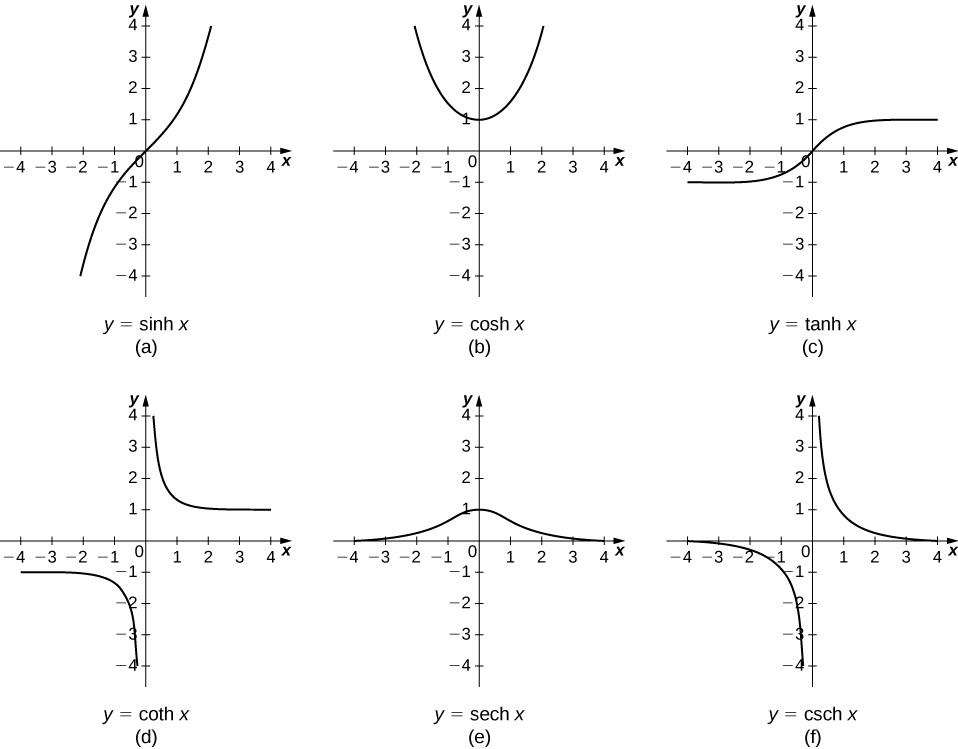
The graphs of the hyperbolic functions are shown in the following figure.

It is easy to develop differentiation formulas for the hyperbolic functions. For example, looking at
we have
Similarly,
We summarize the differentiation formulas for the hyperbolic functions in the following table.
Let’s take a moment to compare the derivatives of the hyperbolic functions with the derivatives of the standard trigonometric functions. There are a lot of similarities, but differences as well. For example, the derivatives of the sine functions match:
and
The derivatives of the cosine functions, however, differ in sign:
but
As we continue our examination of the hyperbolic functions, we must be mindful of their similarities and differences to the standard trigonometric functions.
These differentiation formulas for the hyperbolic functions lead directly to the following integral formulas.
Evaluate the following derivatives:
Using the formulas in [link] and the chain rule, we get
Evaluate the following derivatives:
Use the formulas in [link] and apply the chain rule as necessary.
Evaluate the following integrals:
We can use u-substitution in both cases.
Then,
and
Then,
and
Note that
for all
so we can eliminate the absolute value signs and obtain
Evaluate the following integrals:
Use the formulas above and apply u-substitution as necessary.
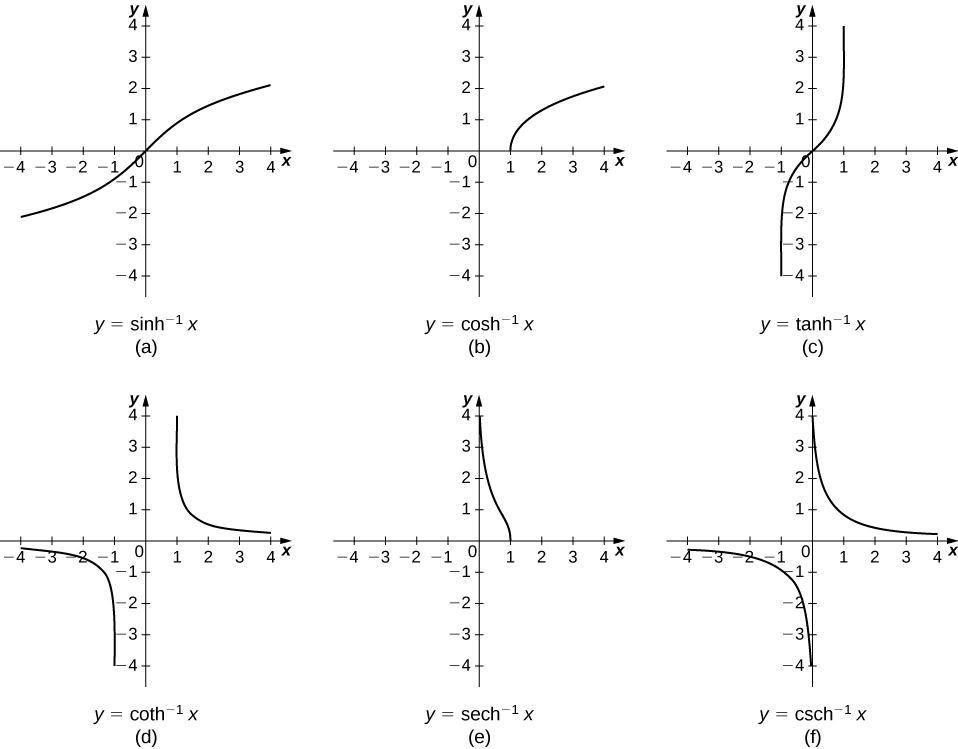
Looking at the graphs of the hyperbolic functions, we see that with appropriate range restrictions, they all have inverses. Most of the necessary range restrictions can be discerned by close examination of the graphs. The domains and ranges of the inverse hyperbolic functions are summarized in the following table.
| Function | Domain | Range |
|---|---|---|
The graphs of the inverse hyperbolic functions are shown in the following figure.
To find the derivatives of the inverse functions, we use implicit differentiation. We have
Recall that
so
Then,
We can derive differentiation formulas for the other inverse hyperbolic functions in a similar fashion. These differentiation formulas are summarized in the following table.
Note that the derivatives of
and
are the same. Thus, when we integrate
we need to select the proper antiderivative based on the domain of the functions and the values of
Integration formulas involving the inverse hyperbolic functions are summarized as follows.
Evaluate the following derivatives:
Using the formulas in [link] and the chain rule, we obtain the following results:
Evaluate the following derivatives:
Use the formulas in [link] and apply the chain rule as necessary.
Evaluate the following integrals:
We can use
in both cases.
Then,
and we have
Then,
and we obtain
Evaluate the following integrals:
Use the formulas above and apply
as necessary.
One physical application of hyperbolic functions involves hanging cables. If a cable of uniform density is suspended between two supports without any load other than its own weight, the cable forms a curve called a catenary. High-voltage power lines, chains hanging between two posts, and strands of a spider’s web all form catenaries. The following figure shows chains hanging from a row of posts.

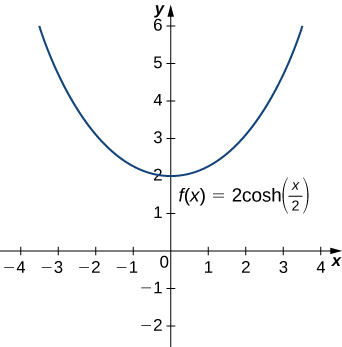
Hyperbolic functions can be used to model catenaries. Specifically, functions of the form
are catenaries. [link] shows the graph of
Assume a hanging cable has the shape
for
where
is measured in feet. Determine the length of the cable (in feet).
Recall from Section
that the formula for arc length is
We have
so
Then
Now recall that
so we have
Assume a hanging cable has the shape
for
Determine the length of the cable (in feet).
Use the procedure from the previous example.
[T] Find expressions for
and
Use a calculator to graph these functions and ensure your expression is correct.
From the definitions of
and
find their antiderivatives.
Show that
and
satisfy
Answers may vary
Use the quotient rule to verify that
Derive
from the definition.
Answers may vary
Take the derivative of the previous expression to find an expression for
Prove
by changing the expression to exponentials.
Answers may vary
Take the derivative of the previous expression to find an expression for
For the following exercises, find the derivatives of the given functions and graph along with the function to ensure your answer is correct.
[T]
[T]
[T]
[T]
[T]
[T]
[T]
[T]
[T]
[T]
For the following exercises, find the antiderivatives for the given functions.
For the following exercises, find the derivatives for the functions.
For the following exercises, find the antiderivatives for the functions.
For the following exercises, use the fact that a falling body with friction equal to velocity squared obeys the equation
Show that
satisfies this equation.
Answers may vary
Derive the previous expression for
by integrating
[T] Estimate how far a body has fallen in
seconds by finding the area underneath the curve of
For the following exercises, use this scenario: A cable hanging under its own weight has a slope
that satisfies
The constant
is the ratio of cable density to tension.
Show that
satisfies this equation.
Integrate
to find the cable height
if
Sketch the cable and determine how far down it sags at
For the following exercises, solve each problem.
[T] A chain hangs from two posts
m apart to form a catenary described by the equation
Find the slope of the catenary at the left fence post.
[T] A chain hangs from two posts four meters apart to form a catenary described by the equation
Find the total length of the catenary (arc length).
[T] A high-voltage power line is a catenary described by
Find the ratio of the area under the catenary to its arc length. What do you notice?
A telephone line is a catenary described by
Find the ratio of the area under the catenary to its arc length. Does this confirm your answer for the previous question?
Prove the formula for the derivative of
by differentiating
(Hint: Use hyperbolic trigonometric identities.)
Prove the formula for the derivative of
by differentiating
(Hint: Use hyperbolic trigonometric identities.)
Prove the formula for the derivative of
by differentiating
(Hint: Use hyperbolic trigonometric identities.)
Prove that
Prove the expression for
Multiply
by
and solve for
Does your expression match the textbook?
Prove the expression for
Multiply
by
and solve for
Does your expression match the textbook?
True or False? Justify your answer with a proof or a counterexample.
The amount of work to pump the water out of a half-full cylinder is half the amount of work to pump the water out of the full cylinder.
False
If the force is constant, the amount of work to move an object from
to
is
The disk method can be used in any situation in which the washer method is successful at finding the volume of a solid of revolution.
False
If the half-life of
is
ms, then
For the following exercises, use the requested method to determine the volume of the solid.
The volume that has a base of the ellipse
and cross-sections of an equilateral triangle perpendicular to the
Use the method of slicing.
from
rotated around they-axis using the washer method
and
rotated around the y-axis using the washer method
rotated around the x-axis using cylindrical shells
For the following exercises, find
a.
b.
c.
[T]
a.
b.
c.
and
and
a.
b.
c.
Below
and above
Find the mass of
on a disk centered at the origin with radius
Find the center of mass for
on
Find the mass and the center of mass of
on the region bounded by
and
Mass:
center of mass:
For the following exercises, find the requested arc lengths.
The length of
for
from
The length of
for
from
to
For the following exercises, find the surface area and volume when the given curves are revolved around the specified axis.
The shape created by revolving the region between
and
rotated around the y-axis.
The loudspeaker created by revolving
from
to
around the x-axis.
Volume:
surface area:
For the following exercises, consider the Karun-3 dam in Iran. Its shape can be approximated as an isosceles triangle with height
m and width
m. Assume the current depth of the water is
m. The density of water is
kg/m
Find the total force on the wall of the dam.
You are a crime scene investigator attempting to determine the time of death of a victim. It is noon and
outside and the temperature of the body is
You know the cooling constant is
When did the victim die, assuming that a human’s temperature is
?
11:02 a.m.
For the following exercise, consider the stock market crash in
in the United States. The table lists the Dow Jones industrial average per year leading up to the crash.
| Years after 1920 | Value ($) |
|---|---|
[T] The best-fit exponential curve to these data is given by
Why do you think the gains of the market were unsustainable? Use first and second derivatives to help justify your answer. What would this model predict the Dow Jones industrial average to be in
?
For the following exercises, consider the catenoid, the only solid of revolution that has a minimal surface, or zero mean curvature. A catenoid in nature can be found when stretching soap between two rings.
Find the volume of the catenoid
from
that is created by rotating this curve around the
as shown here.

Find surface area of the catenoid
from
to
that is created by rotating this curve around the
is a catenary; a cable of uniform density suspended between two supports assumes the shape of a catenary

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: