through an integral.
We already examined exponential functions and logarithms in earlier chapters. However, we glossed over some key details in the previous discussions. For example, we did not study how to treat exponential functions with exponents that are irrational. The definition of the number e is another area where the previous development was somewhat incomplete. We now have the tools to deal with these concepts in a more mathematically rigorous way, and we do so in this section.
For purposes of this section, assume we have not yet defined the natural logarithm, the number e, or any of the integration and differentiation formulas associated with these functions. By the end of the section, we will have studied these concepts in a mathematically rigorous way (and we will see they are consistent with the concepts we learned earlier).
We begin the section by defining the natural logarithm in terms of an integral. This definition forms the foundation for the section. From this definition, we derive differentiation formulas, define the number
and expand these concepts to logarithms and exponential functions of any base.
Recall the power rule for integrals:
Clearly, this does not work when
as it would force us to divide by zero. So, what do we do with
Recall from the Fundamental Theorem of Calculus that
is an antiderivative of
Therefore, we can make the following definition.
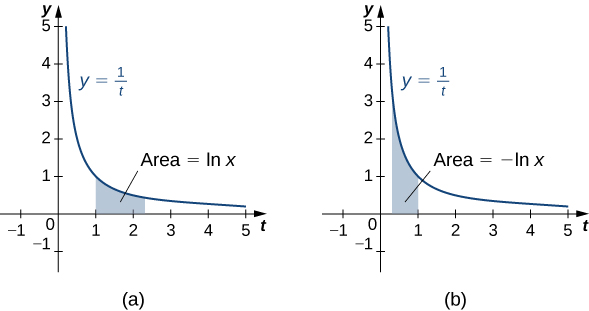
For
define the natural logarithm function by
For
this is just the area under the curve
from
to
For
we have
so in this case it is the negative of the area under the curve from
(see the following figure).

Notice that
Furthermore, the function
for
Therefore, by the properties of integrals, it is clear that
is increasing for
Because of the way we defined the natural logarithm, the following differentiation formula falls out immediately as a result of to the Fundamental Theorem of Calculus.
For
the derivative of the natural logarithm is given by
The function
is differentiable; therefore, it is continuous.
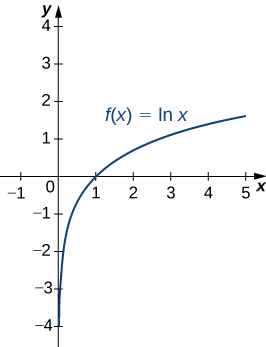
A graph of
is shown in [link]. Notice that it is continuous throughout its domain of
Calculate the following derivatives:
We need to apply the chain rule in both cases.
Calculate the following derivatives:
Apply the differentiation formula just provided and use the chain rule as necessary.
Note that if we use the absolute value function and create a new function
we can extend the domain of the natural logarithm to include
Then
This gives rise to the familiar integration formula.
The natural logarithm is the antiderivative of the function
Calculate the integral
Using
-substitution, let
Then
and we have
Calculate the integral
Apply the integration formula provided earlier and use u-substitution as necessary.
Although we have called our function a “logarithm,” we have not actually proved that any of the properties of logarithms hold for this function. We do so here.
If
and
is a rational number, then
Use
on the last integral in this expression. Let
Then
Furthermore, when
and when
So we get
Furthermore,
Since the derivatives of these two functions are the same, by the Fundamental Theorem of Calculus, they must differ by a constant. So we have
for some constant
Taking
we get
Thus
and the proof is complete. Note that we can extend this property to irrational values of
later in this section.
Part iii. follows from parts ii. and iv. and the proof is left to you.
□
Use properties of logarithms to simplify the following expression into a single logarithm:
We have
Use properties of logarithms to simplify the following expression into a single logarithm:
Apply the properties of logarithms.
Now that we have the natural logarithm defined, we can use that function to define the number
The number
is defined to be the real number such that
To put it another way, the area under the curve
between
and
is
([link]). The proof that such a number exists and is unique is left to you. (Hint: Use the Intermediate Value Theorem to prove existence and the fact that
is increasing to prove uniqueness.)
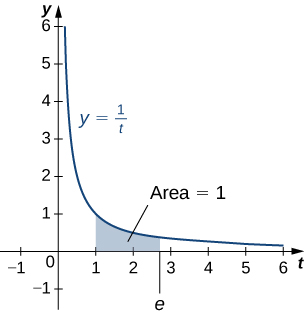
The number
can be shown to be irrational, although we won’t do so here (see the Student Project in Taylor and Maclaurin Series). Its approximate value is given by
We now turn our attention to the function
Note that the natural logarithm is one-to-one and therefore has an inverse function. For now, we denote this inverse function by
Then,
The following figure shows the graphs of
and
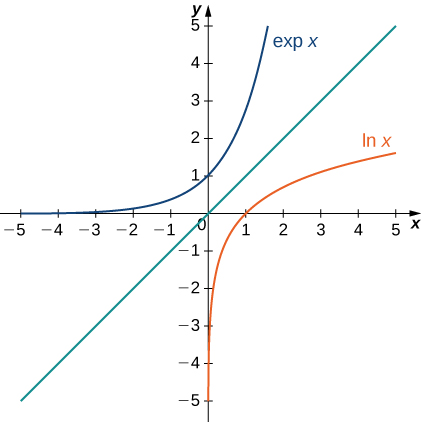
We hypothesize that
For rational values of
this is easy to show. If
is rational, then we have
Thus, when
is rational,
For irrational values of
we simply define
as the inverse function of
For any real number
define
to be the number for which
Then we have
for all
and thus
for all
Since the exponential function was defined in terms of an inverse function, and not in terms of a power of
we must verify that the usual laws of exponents hold for the function
If
and
are any real numbers and
is a rational number, then
Note that if
and
are rational, the properties hold. However, if
or
are irrational, we must apply the inverse function definition of
and verify the properties. Only the first property is verified here; the other two are left to you. We have
Since
is one-to-one, then
□
As with part iv. of the logarithm properties, we can extend property iii. to irrational values of
and we do so by the end of the section.
We also want to verify the differentiation formula for the function
To do this, we need to use implicit differentiation. Let
Then
Thus, we see
as desired, which leads immediately to the integration formula
We apply these formulas in the following examples.
Evaluate the following derivatives:
We apply the chain rule as necessary.
Evaluate the following derivatives:
Use the properties of exponential functions and the chain rule as necessary.
Evaluate the following integral:
Using
-substitution, let
Then
and we have
Evaluate the following integral:
Use the properties of exponential functions and
as necessary.
We close this section by looking at exponential functions and logarithms with bases other than
Exponential functions are functions of the form
Note that unless
we still do not have a mathematically rigorous definition of these functions for irrational exponents. Let’s rectify that here by defining the function
in terms of the exponential function
We then examine logarithms with bases other than
as inverse functions of exponential functions.
For any
and for any real number
define
as follows:
Now
is defined rigorously for all values of x. This definition also allows us to generalize property iv. of logarithms and property iii. of exponential functions to apply to both rational and irrational values of
It is straightforward to show that properties of exponents hold for general exponential functions defined in this way.
Let’s now apply this definition to calculate a differentiation formula for
We have
The corresponding integration formula follows immediately.
Let
Then,
and
If
then the function
is one-to-one and has a well-defined inverse. Its inverse is denoted by
Then,
Note that general logarithm functions can be written in terms of the natural logarithm. Let
Then,
Taking the natural logarithm of both sides of this second equation, we get
Thus, we see that all logarithmic functions are constant multiples of one another. Next, we use this formula to find a differentiation formula for a logarithm with base
Again, let
Then,
Let
Then,
Evaluate the following derivatives:
We need to apply the chain rule as necessary.
Evaluate the following derivatives:
Use the formulas and apply the chain rule as necessary.
Evaluate the following integral:
Use
and let
Then
and we have
Evaluate the following integral:
Use the properties of exponential functions and
as necessary.
is then defined as the inverse of the natural logarithm.
and the corresponding inverse functions are general logarithms.
Z
Z
For the following exercises, find the derivative
For the following exercises, find the indefinite integral.
For the following exercises, find the derivative
(You can use a calculator to plot the function and the derivative to confirm that it is correct.)
[T]
[T]
[T]
[T]
[T]
[T]
[T]
[T]
[T]
[T]
For the following exercises, find the definite or indefinite integral.
For the following exercises, compute
by differentiating
For the following exercises, evaluate by any method.
For the following exercises, use the function
If you are unable to find intersection points analytically, use a calculator.
Find the area of the region enclosed by
and
above
[T] Find the arc length of
from
to
Find the area between
and the x-axis from
Find the volume of the shape created when rotating this curve from
around the x-axis, as pictured here.
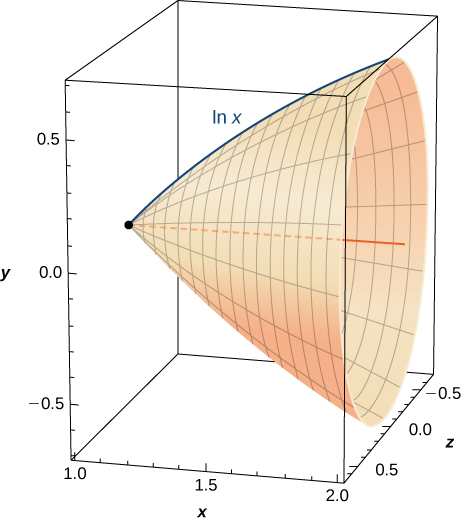
[T] Find the surface area of the shape created when rotating the curve in the previous exercise from
to
around the x-axis.
If you are unable to find intersection points analytically in the following exercises, use a calculator.
Find the area of the hyperbolic quarter-circle enclosed by
above
[T] Find the arc length of
from
Find the area under
and above the x-axis from
For the following exercises, verify the derivatives and antiderivatives.

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: