Areas between Curves

In Introduction to Integration, we developed the concept of the definite integral to calculate the area below a curve on a given interval. In this section, we expand that idea to calculate the area of more complex regions. We start by finding the area between two curves that are functions of x,

beginning with the simple case in which one function value is always greater than the other. We then look at cases when the graphs of the functions cross. Last, we consider how to calculate the area between two curves that are functions of y.

Area of a Region between Two Curves

Let f(x)

and g(x)

be continuous functions over an interval [a,b]

such that f(x)≥g(x)

on [a,b].

We want to find the area between the graphs of the functions, as shown in the following figure.

This figure is a graph in the first quadrant. There are two curves on the graph. The higher curve is labeled “f(x)” and the lower curve is labeled “g(x)”. There are two boundaries on the x-axis labeled a and b. There is shaded area between the two curves bounded by lines at x=a and x=b.

As we did before, we are going to partition the interval on the x-axis

and approximate the area between the graphs of the functions with rectangles. So, for i=0,1,2,…,n,

let P={xi}

be a regular partition of [a,b].

Then, for i=1,2,…,n,

choose a point xi*∈[xi−1,xi],

and on each interval [xi−1,xi]

construct a rectangle that extends vertically from g(xi*)

to f(xi*).

[link](a) shows the rectangles when xi*

is selected to be the left endpoint of the interval and n=10.

[link](b) shows a representative rectangle in detail.

Use this calculator to learn more about the areas between two curves.

This figure has three graphs. The first graph has two curves, one over the other. In between the curves is a rectangle. The top of the rectangle is on the upper curve labeled “f(x*)” and the bottom of the rectangle is on the lower curve and labeled “g(x*)”. The second graph, labeled “(a)”, has two curves on the graph. The higher curve is labeled “f(x)” and the lower curve is labeled “g(x)”. There are two boundaries on the x-axis labeled a and b. There is shaded area between the two curves bounded by lines at x=a and x=b. The third graph, labeled “(b)” has two curves one over the other. The first curve is labeled “f(x*)” and the lower curve is labeled “g(x*)”. There is a shaded rectangle between the two. The width of the rectangle is labeled as “delta x”.

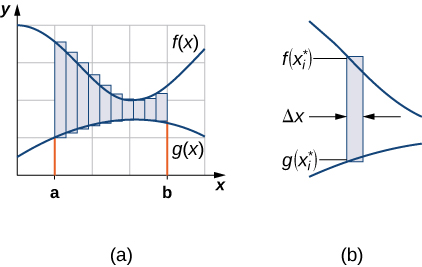
The height of each individual rectangle is f(xi*)−g(xi*)

and the width of each rectangle is Δx.

Adding the areas of all the rectangles, we see that the area between the curves is approximated by

A≈∑i=1n[f(xi*)−g(xi*)]Δx.

This is a Riemann sum, so we take the limit as n→∞

and we get

A=limn→∞∑i=1n[f(xi*)−g(xi*)]Δx=∫ab[f(x)−g(x)]dx.

These findings are summarized in the following theorem.

Finding the Area between Two Curves

Let f(x)

and g(x)

be continuous functions such that f(x)≥g(x)

over an interval [a,b].

Let R

denote the region bounded above by the graph of f(x),

below by the graph of g(x),

and on the left and right by the lines x=a

and x=b,

respectively. Then, the area of R

is given by

A=∫ab[f(x)−g(x)]dx.

We apply this theorem in the following example.

Finding the Area of a Region between Two Curves 1

If R is the region bounded above by the graph of the function f(x)=x+4

and below by the graph of the function g(x)=3−x2

over the interval [1,4],

find the area of region R.

The region is depicted in the following figure.

This figure is has two linear graphs in the first quadrant. They are the functions f(x) = x+4 and g(x)= 3-x/2. In between these lines is a shaded region, bounded above by f(x) and below by g(x). The shaded area is between x=1 and x=4.

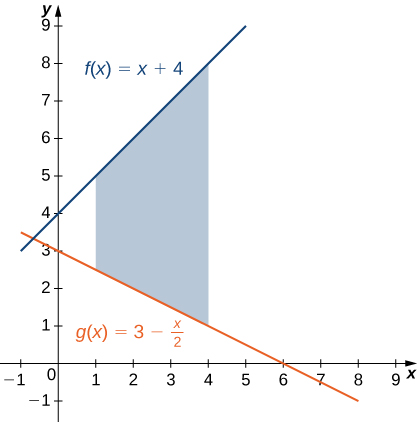
We have

A=∫ab[f(x)−g(x)]dx=∫14[(x+4)−(3−x2)]dx=∫14[3x2+1]dx=[3x24+x]\|14=(16−74)=574.

The area of the region is 574units2.

If R

is the region bounded by the graphs of the functions f(x)=x2+5

and g(x)=x+12

over the interval [1,5],

find the area of region R.

12

units2

Hint

Graph the functions to determine which function’s graph forms the upper bound and which forms the lower bound, then follow the process used in [link].

In [link], we defined the interval of interest as part of the problem statement. Quite often, though, we want to define our interval of interest based on where the graphs of the two functions intersect. This is illustrated in the following example.

Finding the Area of a Region between Two Curves 2

If R

is the region bounded above by the graph of the function f(x)=9−(x/2)2

and below by the graph of the function g(x)=6−x,

find the area of region R.

The region is depicted in the following figure.

This figure is has two graphs in the first quadrant. They are the functions f(x) = 9-(x/2)^2 and g(x)= 6-x. In between these graphs, an upside down parabola and a line, is a shaded region, bounded above by f(x) and below by g(x).

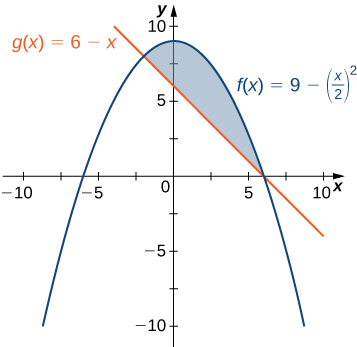
We first need to compute where the graphs of the functions intersect. Setting f(x)=g(x),

we get

f(x)=g(x)9−(x2)2=6−x9−x24=6−x36−x2=24−4xx2−4x−12=0(x−6)(x+2)=0.

The graphs of the functions intersect when x=6

or x=−2,

so we want to integrate from −2

to 6.

Since f(x)≥g(x)

for −2≤x≤6,

we obtain

A=∫ab[f(x)−g(x)]dx=∫−26[9−(x2)2−(6−x)]dx=∫−26[3−x24+x]dx=[3x−x312+x22]\|−26=643.

The area of the region is 64/3

units2.

If R is the region bounded above by the graph of the function f(x)=x

and below by the graph of the function g(x)=x4,

find the area of region R.

310

unit2

Hint

Use the process from [link].

Areas of Compound Regions

So far, we have required f(x)≥g(x)

over the entire interval of interest, but what if we want to look at regions bounded by the graphs of functions that cross one another? In that case, we modify the process we just developed by using the absolute value function.

Finding the Area of a Region between Curves That Cross

Let f(x)

and g(x)

be continuous functions over an interval [a,b].

Let R

denote the region between the graphs of f(x)

and g(x),

and be bounded on the left and right by the lines x=a

and x=b,

respectively. Then, the area of R

is given by

A=∫ab\|f(x)−g(x)\|dx.

In practice, applying this theorem requires us to break up the interval [a,b]

and evaluate several integrals, depending on which of the function values is greater over a given part of the interval. We study this process in the following example.

Finding the Area of a Region Bounded by Functions That Cross

If R is the region between the graphs of the functions f(x)=sinx

and g(x)=cosx

over the interval [0,π],

find the area of region R.

The region is depicted in the following figure.

This figure is has two graphs. They are the functions f(x) = sinx and g(x)= cosx. They are both periodic functions that resemble waves. There are two shaded areas between the graphs. The first shaded area is labeled “R1” and has g(x) above f(x). This region begins at the y-axis and stops where the curves intersect. The second region is labeled “R2” and begins at the intersection with f(x) above g(x). The shaded region stops at x=pi.

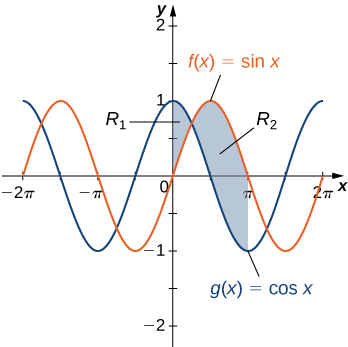
The graphs of the functions intersect at x=π/4.

For x∈[0,π/4],

cosx≥sinx,

so

\|f(x)−g(x)\|=\|sinx−cosx\|=cosx−sinx.

On the other hand, for x∈[π/4,π],

sinx≥cosx,

so

\|f(x)−g(x)\|=\|sinx−cosx\|=sinx−cosx.

Then

A=∫ab\|f(x)−g(x)\|dx=∫0π\|sinx−cosx\|dx=∫0π/4(cosx−sinx)dx+∫π/4π(sinx−cosx)dx=[sinx+cosx]\|0π/4+[−cosx−sinx]\|π/4π=(2−1)+(1+2)=22.

The area of the region is 22

units2.

If R is the region between the graphs of the functions f(x)=sinx

and g(x)=cosx

over the interval [π/2,2π],

find the area of region R.

2+22

units2

Hint

The two curves intersect at x=(5π)/4.

Finding the Area of a Complex Region

Consider the region depicted in [link]. Find the area of R.

This figure is has two graphs in the first quadrant. They are the functions f(x) = x^2 and g(x)= 2-x. In between these graphs is a shaded region, bounded to the left by f(x) and to the right by g(x). All of which is above the x-axis. The region is labeled R. The shaded area is between x=0 and x=2.

As with [link], we need to divide the interval into two pieces. The graphs of the functions intersect at x=1

(set f(x)=g(x)

and solve for x), so we evaluate two separate integrals: one over the interval [0,1]

and one over the interval [1,2].

Over the interval [0,1],

the region is bounded above by f(x)=x2

and below by the x-axis, so we have

A1=∫01x2dx=x33\|01=13.

Over the interval [1,2],

the region is bounded above by g(x)=2−x

and below by the x-axis,

so we have

A2=∫12(2−x)dx=[2x−x22]\|12=12.

Adding these areas together, we obtain

A=A1+A2=13+12=56.

The area of the region is 5/6

units2.

Consider the region depicted in the following figure. Find the area of R.

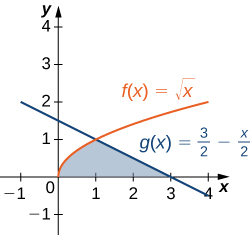
This figure is has two graphs in the first quadrant. They are the functions f(x) = squareroot of x and g(x)= 3/2 – x/2. In between these graphs is a shaded region, bounded to the left by f(x) and to the right by g(x). All of which is above the x-axis. The shaded area is between x=0 and x=3.

53

units2

Hint

The two curves intersect at x=1.

Regions Defined with Respect to y

In [link], we had to evaluate two separate integrals to calculate the area of the region. However, there is another approach that requires only one integral. What if we treat the curves as functions of y,

instead of as functions of x?

Review [link]. Note that the left graph, shown in red, is represented by the function y=f(x)=x2.

We could just as easily solve this for x

and represent the curve by the function x=v(y)=y.

(Note that x=−y

is also a valid representation of the function y=f(x)=x2

as a function of y.

However, based on the graph, it is clear we are interested in the positive square root.) Similarly, the right graph is represented by the function y=g(x)=2−x,

but could just as easily be represented by the function x=u(y)=2−y.

When the graphs are represented as functions of y,

we see the region is bounded on the left by the graph of one function and on the right by the graph of the other function. Therefore, if we integrate with respect to y,

we need to evaluate one integral only. Let’s develop a formula for this type of integration.

Let u(y)

and v(y)

be continuous functions over an interval [c,d]

such that u(y)≥v(y)

for all y∈[c,d].

We want to find the area between the graphs of the functions, as shown in the following figure.

This figure is has two graphs in the first quadrant. They are the functions v(y) and u(y). In between these graphs is a shaded region, bounded to the left by v(y) and to the right by u(y). The region is labeled R. The shaded area is between the horizontal boundaries of y=c and y=d.

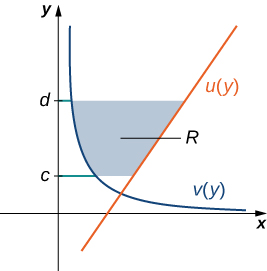
This time, we are going to partition the interval on the y-axis

and use horizontal rectangles to approximate the area between the functions. So, for i=0,1,2,…,n,

let Q={yi}

be a regular partition of [c,d].

Then, for i=1,2,…,n,

choose a point yi*∈[yi−1,yi],

then over each interval [yi−1,yi]

construct a rectangle that extends horizontally from v(yi*)

to u(yi*).

[link](a) shows the rectangles when yi*

is selected to be the lower endpoint of the interval and n=10.

[link](b) shows a representative rectangle in detail.

This figure is has three graphs. The first figure has two curves. They are the functions v(y*) and u(y*). In between these curves is a horizontal rectangle. The second figure labeled “(a)”, is a shaded region, bounded to the left by v(y) and to the right by u(y). The shaded area is between the horizontal boundaries of y=c and y=d. This shaded area is broken into rectangles between the curves. The third figure, labeled “(b)”, is the two curves v(y*) and u(y*). In between the curves is a horizontal rectangle with width delta y.

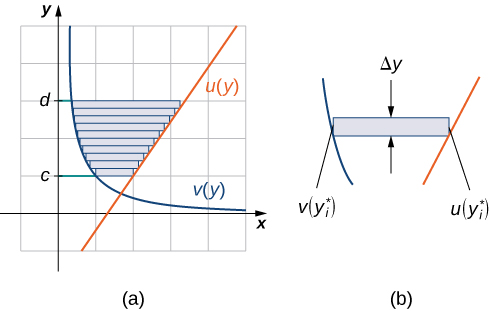
The height of each individual rectangle is Δy

and the width of each rectangle is u(yi*)−v(yi*).

Therefore, the area between the curves is approximately

A≈∑i=1n[u(yi*)−v(yi*)]Δy.

This is a Riemann sum, so we take the limit as n→∞,

obtaining

A=limn→∞∑i=1n[u(yi*)−v(yi*)]Δy=∫cd[u(y)−v(y)]dy.

These findings are summarized in the following theorem.

Finding the Area between Two Curves, Integrating along the *y*-axis

Let u(y)

and v(y)

be continuous functions such that u(y)≥v(y)

for all y∈[c,d].

Let R

denote the region bounded on the right by the graph of u(y),

on the left by the graph of v(y),

and above and below by the lines y=d

and y=c,

respectively. Then, the area of R

is given by

A=∫cd[u(y)−v(y)]dy.
Integrating with Respect to *y*

Let’s revisit [link], only this time let’s integrate with respect to y.

Let R

be the region depicted in [link]. Find the area of R

by integrating with respect to y.

This figure is has two graphs in the first quadrant. They are the functions f(x) = x^2 and g(x)= 2-x. In between these graphs is a shaded region, bounded to the left by f(x) and to the right by g(x). All of which is above the x-axis. The region is labeled R. The shaded area is between x=0 and x=2.

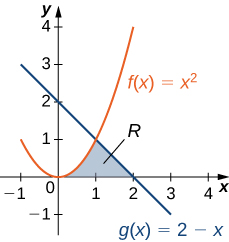
We must first express the graphs as functions of y.

As we saw at the beginning of this section, the curve on the left can be represented by the function x=v(y)=y,

and the curve on the right can be represented by the function x=u(y)=2−y.

Now we have to determine the limits of integration. The region is bounded below by the x-axis, so the lower limit of integration is y=0.

The upper limit of integration is determined by the point where the two graphs intersect, which is the point (1,1),

so the upper limit of integration is y=1.

Thus, we have [c,d]=[0,1].

Calculating the area of the region, we get

A=∫cd[u(y)−v(y)]dy=∫01[(2−y)−y]dy=[2y−y22−23y3/2]\|01=56.

The area of the region is 5/6

units2.

Let’s revisit the checkpoint associated with [link], only this time, let’s integrate with respect to y.

Let be the region depicted in the following figure. Find the area of R

by integrating with respect to y.

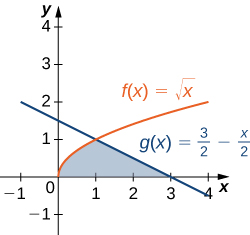
This figure is has two graphs in the first quadrant. They are the functions f(x) = squareroot of x and g(x)= 3/2 – x/2. In between these graphs is a shaded region, bounded to the left by f(x) and to the right by g(x). All of which is above the x-axis. The shaded area is between x=0 and x=3.

53

units2

Hint

Follow the process from the previous example.

Key Concepts

Key Equations

For the following exercises, determine the area of the region between the two curves in the given figure by integrating over the x-axis.

y=x2−3andy=1

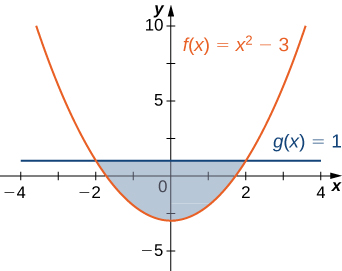
This figure is has two graphs. They are the functions f(x) = x^2-3and g(x)=1. In between these graphs is a shaded region, bounded above by g(x) and below by f(x). The shaded area is between x=-2 and x=2.

323
y=x2andy=3x+4

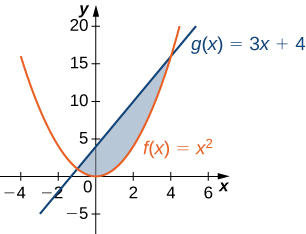
This figure is has two graphs. They are the functions f(x) = x^2 and g(x)= 3x+4. In between these graphs is a shaded region, bounded above by g(x) and below by g(x).

For the following exercises, split the region between the two curves into two smaller regions, then determine the area by integrating over the x-axis.

Note that you will have two integrals to solve.

y=x3

and y=x2+x

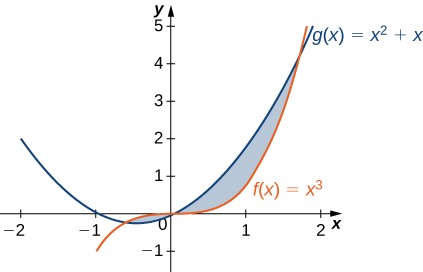
This figure is has two graphs. They are the functions f(x) = x^3 and g(x)= x^2+x. These graphs intersect twice. The regions between the intersections are shaded. The first region is bounded above by f(x) and below by g(x). The second region is bounded above by g(x) and below by f(x).

1312
y=cosθ

and y=0.5,

for 0≤θ≤π

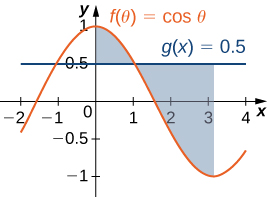
This figure is has two graphs. They are the functions f(theta) = cos(theta) and g(x)= 0.5. These graphs intersect twice. The regions between the intersections are shaded. The first region is bounded above by f(x) and below by g(x). The second region is bounded above by g(x) and below by f(x).

For the following exercises, determine the area of the region between the two curves by integrating over the y-axis.

x=y2andx=9

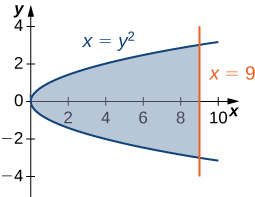
This figure is has two graphs. They are the equations x=y^2 and x=9. The region between the graphs is shaded. It is horizontal, between the y-axis and the line x=9.

36
y=xandx=y2

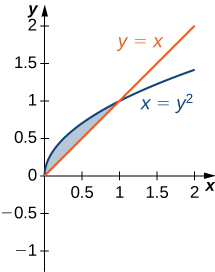
This figure is has two graphs. They are the equations y=x and x=y^2. The region between the graphs is shaded, bounded above by x=y^2 and below by y=x.

For the following exercises, graph the equations and shade the area of the region between the curves. Determine its area by integrating over the x-axis.

y=x2andy=−x2+18x

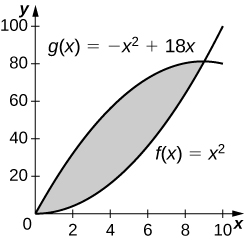
This figure is has two graphs. They are the functions f(x)=x^2 and g(x)=-x^2+18x. The region between the graphs is shaded, bounded above by g(x) and below by f(x). It is in the first quadrant.

243 square units

y=1x,y=1x2,andx=3
y=cosx

and y=cos2x

on x=[−π,π]

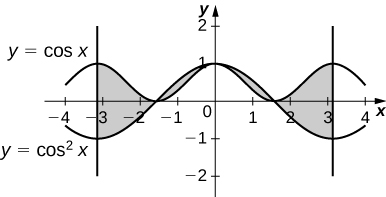
This figure is has two graphs. They are the functions y=cos(x) and y=cos^2(x). The graphs are periodic and resemble waves. There are four regions created by intersections of the curves. The areas are shaded.

4

y=ex,y=e2x−1,andx=0
y=ex,y=e−x,x=−1andx=1

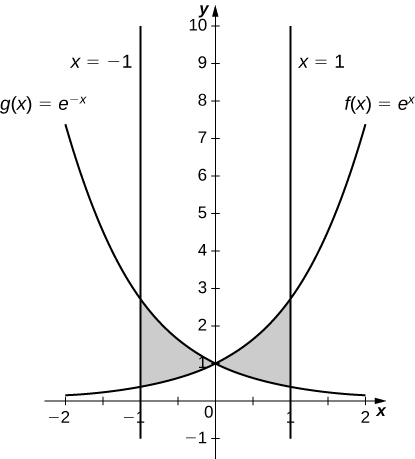
This figure is has two graphs. They are the functions f(x)=e^x and g(x)=e^-x. There are two shaded regions. In the second quadrant the region is bounded by x=-1, g(x) above and f(x) below. The second region is in the first quadrant and is bounded by f(x) above, g(x) below, and x=1.

2(e−1)2e
y=e,y=ex,andy=e−x
y=\|x\|andy=x2

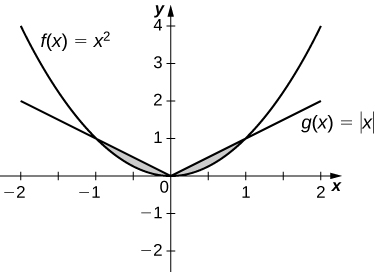
This figure is has two graphs. They are the functions f(x)=x^2 and g(x)=absolute value of x. There are two shaded regions. The first region is in the second quadrant and is between g(x) above and f(x) below. The second region is in the first quadrant and is bounded above by g(x) and below by f(x).

13

For the following exercises, graph the equations and shade the area of the region between the curves. If necessary, break the region into sub-regions to determine its entire area.

y=sin(πx),y=2x,andx>0
y=12−x,y=x,andy=1

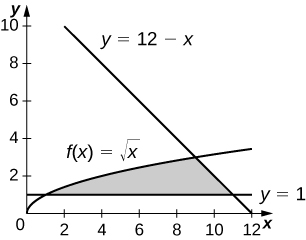
This figure is has three graphs. They are the functions f(x)=squareroot of x, y=12-x, and y=1. The region between the graphs is shaded, bounded above and to the left by f(x), above and to the right by the line y=12-x, and below by the line y=1. It is in the first quadrant.

343
y=sinx

and y=cosx

over x=[−π,π]

y=x3andy=x2−2x

over x=[−1,1]

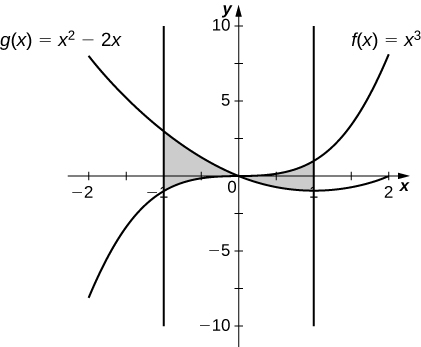
This figure is has two graphs. They are the functions f(x)=x^3 and g(x)=x^2-2x. There are two shaded regions between the graphs. The first region is bounded to the left by the line x=-2, above by g(x) and below by f(x). The second region is bounded above by f(x), below by g(x) and to the right by the line x=2.

52
y=x2+9andy=10+2x

over x=[−1,3]

y=x3+3x

and y=4x

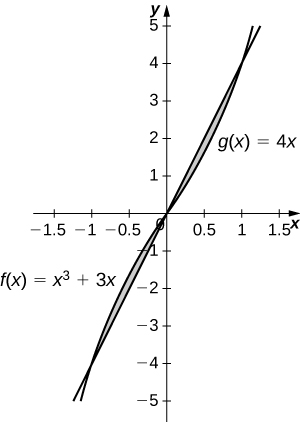
This figure is has two graphs. They are the functions f(x)=x^3+3x and g(x)=4x. There are two shaded regions between the graphs. The first region is bounded above by f(x) and below by g(x). The second region is bounded above by g(x), below by f(x).

12

For the following exercises, graph the equations and shade the area of the region between the curves. Determine its area by integrating over the y-axis.

x=y3andx=3y−2
x=2yandx=y3−y

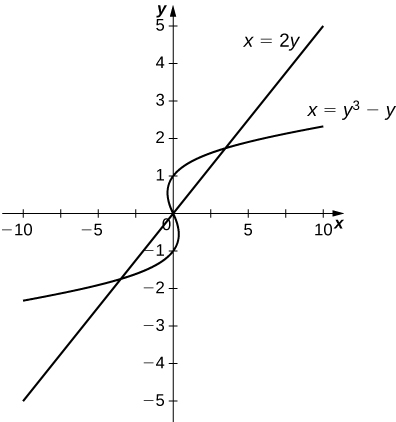
This figure is has two graphs. They are the equations x=2y and x=y^3-y. The graphs intersect in the third quadrant and again in the first quadrant forming two closed regions in between them.

92
x=−3+y2andx=y−y2
y2=xandx=y+2

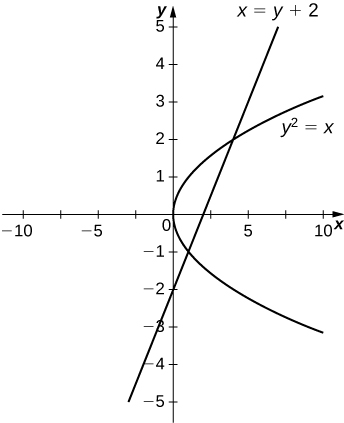
This figure is has two graphs. They are the equations x=y+2 and y^2=x. The graphs intersect, forming a region in between them

92
x=\|y\|and2x=−y2+2
x=siny,x=cos(2y),y=π/2,andy=−π/2

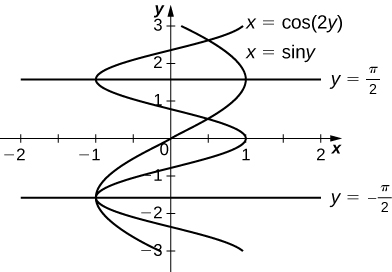
This figure is has two graphs. They are the equations x=cos(y) and x=sin(y). The graphs intersect, forming two regions bounded above by the line y=pi/2 and below by the line y=-pi/2.

332

For the following exercises, graph the equations and shade the area of the region between the curves. Determine its area by integrating over the x-axis or y-axis, whichever seems more convenient.

x=y4andx=y5
y=xex,y=ex,x=0,andx=1

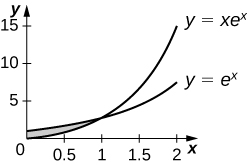
This figure is has two graphs. They are the equations y=xe^x and y=e^x. The graphs intersect, forming a region in between them in the first quadrant.

e−2
y=x6andy=x4
x=y3+2y2+1andx=−y2+1

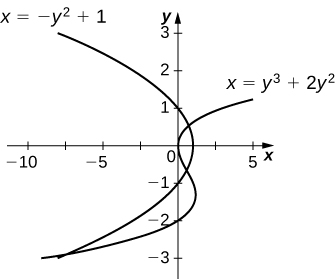
This figure is has two graphs. They are the equations x=-y^2+1 and x=y^3+2y^2. The graphs intersect, forming two regions in between them.

274
y=\|x\|andy=x2−1
y=4−3xandy=1x

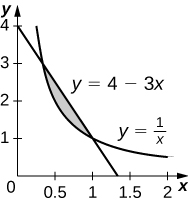
This figure is has two graphs. They are the equations y=4-3x and y=1/x. The graphs intersect, having region between them shaded. The region is in the first quadrant.

43−ln(3)
y=sinx,x=−π/6,x=π/6,andy=cos3x
y=x2−3x+2andy=x3−2x2−x+2

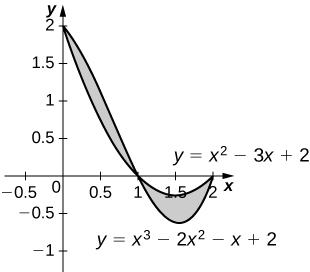
This figure is has two graphs. They are the equations y=x^2-3x+2 and y=x^3-2x^2-x+2. The graphs intersect, having region between them shaded.

12
y=2cos3(3x),y=−1,x=π4,andx=−π4
y+y3=xand2y=x

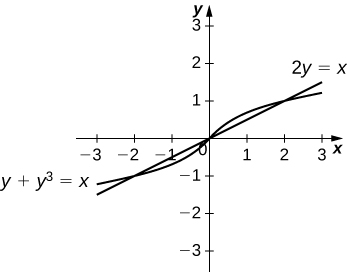
This figure is has two graphs. They are the equations 2y=x and y+y^3=x. The graphs intersect, forming two regions. The regions are shaded.

12
y=1−x2andy=x2−1
y=cos−1x,y=sin−1x,x=−1,andx=1

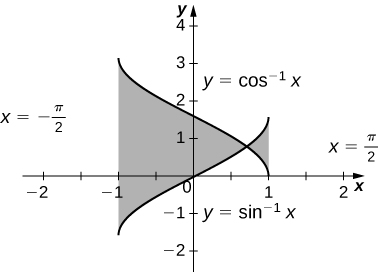
This figure is has two graphs. They are the equations y=arccos(x) and y=arcsin (x). The graphs intersect, forming two regions. The first region is bounded to the left by x=-1. The second region is bounded to the right by x=1. Both regions are shaded.

−2(2−π)

For the following exercises, find the exact area of the region bounded by the given equations if possible. If you are unable to determine the intersection points analytically, use a calculator to approximate the intersection points with three decimal places and determine the approximate area of the region.

[T] x=eyandy=x−2

[T] y=x2andy=1−x2

1.067

[T] y=3x2+8x+9and3y=x+24

[T] x=4−y2andy2=1+x2

0.852

[T] x2=y3andx=3y

[T] y=sin3x+2,y=tanx,x=−1.5,andx=1.5

7.523

[T] y=1−x2andy2=x2

[T] y=1−x2andy=x2+2x+1

3π−412

[T] x=4−y2andx=1+3y+y2

[T] y=cosx,y=ex,x=−π,andx=0

1.429

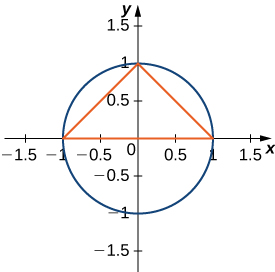
The largest triangle with a base on the x-axis

that fits inside the upper half of the unit circle y2+x2=1

is given by y=1+x

and y=1−x.

See the following figure. What is the area inside the semicircle but outside the triangle?

This figure is has the graph of a circle with center at the origin and radius of 1. There is a triangle inscribed with base on the x-axis from -1 to 1 and the third corner at the point y=1.

A factory selling cell phones has a marginal cost function C(x)=0.01x2−3x+229,

where x

represents the number of cell phones, and a marginal revenue function given by R(x)=429−2x.

Find the area between the graphs of these curves and x=0.

What does this area represent?

$33,333.33

total profit for 200

cell phones sold

An amusement park has a marginal cost function C(x)=1000e−x+5,

where x

represents the number of tickets sold, and a marginal revenue function given by R(x)=60−0.1x.

Find the total profit generated when selling 550

tickets. Use a calculator to determine intersection points, if necessary, to two decimal places.

The tortoise versus the hare: The speed of the hare is given by the sinusoidal function H(t)=1−cos((πt)/2)

whereas the speed of the tortoise is T(t)=(1/2)tan−1(t/4),

where t

is time measured in hours and the speed is measured in miles per hour. Find the area between the curves from time t=0

to the first time after one hour when the tortoise and hare are traveling at the same speed. What does it represent? Use a calculator to determine the intersection points, if necessary, accurate to three decimal places.

3.263

mi represents how far ahead the hare is from the tortoise

The tortoise versus the hare: The speed of the hare is given by the sinusoidal function H(t)=(1/2)−(1/2)cos(2πt)

whereas the speed of the tortoise is T(t)=t,

where t

is time measured in hours and speed is measured in kilometers per hour. If the race is over in 1

hour, who won the race and by how much? Use a calculator to determine the intersection points, if necessary, accurate to three decimal places.

For the following exercises, find the area between the curves by integrating with respect to x

and then with respect to y.

Is one method easier than the other? Do you obtain the same answer?

y=x2+2x+1andy=−x2−3x+4
34324
y=x4andx=y5
x=y2−2andx=2y
43

For the following exercises, solve using calculus, then check your answer with geometry.

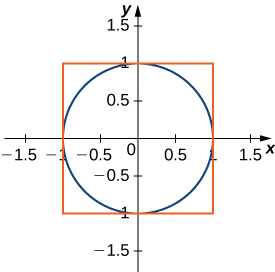
Determine the equations for the sides of the square that touches the unit circle on all four sides, as seen in the following figure. Find the area between the perimeter of this square and the unit circle. Is there another way to solve this without using calculus?

This figure is the graph of a circle centered at the origin with radius of 1. There is a circumscribed square around the circle.

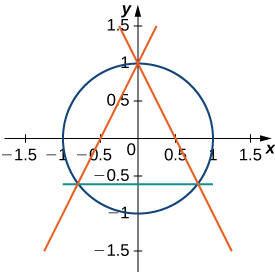
Find the area between the perimeter of the unit circle and the triangle created from y=2x+1,y=1−2x

and y=−35,

as seen in the following figure. Is there a way to solve this without using calculus?

This figure is the graph of a circle centered at the origin with radius of 1. There are three lines intersecting the circle. The lines intersect the circle at three points to form a triangle within the circle.

π−3225
Creative Commons License
This work is licensed under a Creative Commons Attribution 4.0 International License.

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1

Attribution: