Integrals Resulting in Inverse Trigonometric Functions
- Integrate functions resulting in inverse trigonometric functions
In this section we focus on integrals that result in inverse trigonometric functions. We have worked with these functions before. Recall from Functions and Graphs that trigonometric functions are not one-to-one unless the domains are restricted. When working with inverses of trigonometric functions, we always need to be careful to take these restrictions into account. Also in Derivatives, we developed formulas for derivatives of inverse trigonometric functions. The formulas developed there give rise directly to integration formulas involving inverse trigonometric functions.
Integrals that Result in Inverse Sine Functions
Let us begin this last section of the chapter with the three formulas. Along with these formulas, we use substitution to evaluate the integrals. We prove the formula for the inverse sine integral.
Rule: Integration Formulas Resulting in Inverse Trigonometric Functions
The following integration formulas yield inverse trigonometric functions:
-
-
-
Proof
Let
Then
Now let’s use implicit differentiation. We obtain
For
Thus, applying the Pythagorean identity
we have
This gives
Then for
we have
□
Evaluating a Definite Integral Using Inverse Trigonometric Functions
Evaluate the definite integral
We can go directly to the formula for the antiderivative in the rule on integration formulas resulting in inverse trigonometric functions, and then evaluate the definite integral. We have
Find the antiderivative of
Finding an Antiderivative Involving an Inverse Trigonometric Function
Evaluate the integral
Substitute
Then
and we have
Applying the formula with
we obtain
Find the indefinite integral using an inverse trigonometric function and substitution for
Hint
Use the formula in the rule on integration formulas resulting in inverse trigonometric functions.
Evaluating a Definite Integral
Evaluate the definite integral
The format of the problem matches the inverse sine formula. Thus,
Integrals Resulting in Other Inverse Trigonometric Functions
There are six inverse trigonometric functions. However, only three integration formulas are noted in the rule on integration formulas resulting in inverse trigonometric functions because the remaining three are negative versions of the ones we use. The only difference is whether the integrand is positive or negative. Rather than memorizing three more formulas, if the integrand is negative, simply factor out −1 and evaluate the integral using one of the formulas already provided. To close this section, we examine one more formula: the integral resulting in the inverse tangent function.
Finding an Antiderivative Involving the Inverse Tangent Function
Find an antiderivative of
Comparing this problem with the formulas stated in the rule on integration formulas resulting in inverse trigonometric functions, the integrand looks similar to the formula for
So we use substitution, letting
then
and
Then, we have
Use substitution to find the antiderivative of
Hint
Use the solving strategy from [link] and the rule on integration formulas resulting in inverse trigonometric functions.
Applying the Integration Formulas
Find the antiderivative of
Apply the formula with
Then,
Find the antiderivative of
Hint
Follow the steps in [link].
Evaluating a Definite Integral
Evaluate the definite integral
Use the formula for the inverse tangent. We have
Evaluate the definite integral
Hint
Follow the procedures from [link] to solve the problem.
Key Concepts
- Formulas for derivatives of inverse trigonometric functions developed in Derivatives of Exponential and Logarithmic Functions lead directly to integration formulas involving inverse trigonometric functions.
- Use the formulas listed in the rule on integration formulas resulting in inverse trigonometric functions to match up the correct format and make alterations as necessary to solve the problem.
- Substitution is often required to put the integrand in the correct form.
Key Equations
- Integrals That Produce Inverse Trigonometric Functions
In the following exercises, evaluate each integral in terms of an inverse trigonometric function.
In the following exercises, find each indefinite integral, using appropriate substitutions.
Explain the relationship
Is it true, in general, that
So,
They differ by a constant.
Explain the relationship
Is it true, in general, that
Explain what is wrong with the following integral:
is not defined as a real number when
Explain what is wrong with the following integral:
In the following exercises, solve for the antiderivative
of f with
then use a calculator to graph f and the antiderivative over the given interval
Identify a value of C such that adding C to the antiderivative recovers the definite integral
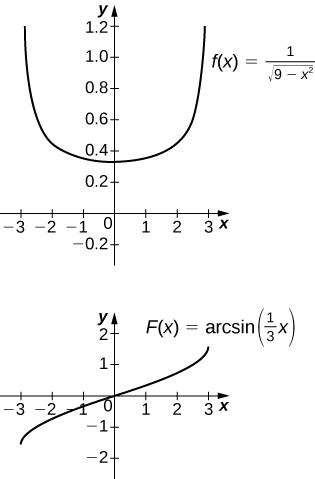
The antiderivative is
Taking
recovers the definite integral.
[T]
over
![Two graphs. The first shows the function f(x) = cos(x) / (4 + sin(x)^2). It is an oscillating function over [-6, 6] with turning points at roughly (-3, -2.5), (0, .25), and (3, -2.5), where (0,.25) is a local max and the others are local mins. The second shows the function F(x) = .5 * arctan(.5*sin(x)), which also oscillates over [-6,6]. It has turning points at roughly (-4.5, .25), (-1.5, -.25), (1.5, .25), and (4.5, -.25).](../resources/CNX_Calc_Figure_05_07_203.jpg)
The antiderivative is
Taking
recovers the definite integral.
[T]
over
In the following exercises, compute the antiderivative using appropriate substitutions.
In the following exercises, use a calculator to graph the antiderivative
with
over the given interval
Approximate a value of C, if possible, such that adding C to the antiderivative gives the same value as the definite integral
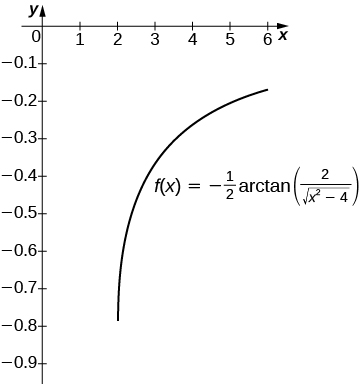
The antiderivative is
Taking
recovers the definite integral over
[T]
over
[T]
over
![The graph of f(x) = arctan(x sin(x)) over [-6,6]. It has five turning points at roughly (-5, -1.5), (-2,1), (0,0), (2,1), and (5,-1.5).](../resources/CNX_Calc_Figure_05_07_207.jpg)
The general antiderivative is
Taking
recovers the definite integral.
[T]
over
![A graph of the function f(x) = arctan(ln(x)) over (0, 2]. It is an increasing curve with x-intercept at (1,0).](../resources/CNX_Calc_Figure_05_07_209.jpg)
The general antiderivative is
Taking
recovers the definite integral.
[T]
over
In the following exercises, compute each integral using appropriate substitutions.
In the following exercises, compute each definite integral.
For
compute
and evaluate
the area under the graph of
on
For
compute
and evaluate
the area under the graph of
over
Use the substitution
and the identity
to evaluate
(Hint: Multiply the top and bottom of the integrand by
Using the hint, one has
Set
Then,
and the integral is
If one uses the identity
then this can also be written
[T] Approximate the points at which the graphs of
and
intersect, and approximate the area between their graphs accurate to three decimal places.
47. [T] Approximate the points at which the graphs of
and
intersect, and approximate the area between their graphs accurate to three decimal places.
The left endpoint estimate with
is 2.796 and these decimals persist for
Use the following graph to prove that
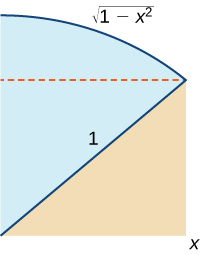
Chapter Review Exercises
True or False. Justify your answer with a proof or a counterexample. Assume all functions
and
are continuous over their domains.
If
for all
then the right-hand rule underestimates the integral
Use a graph to justify your answer.
If
for all
then
All continuous functions have an antiderivative.
Evaluate the Riemann sums
for the following functions over the specified interval. Compare your answer with the exact answer, when possible, or use a calculator to determine the answer.
exact answer: 4
exact answer: 5.870
Evaluate the following integrals.
Find the antiderivative.
Find the derivative.
The following problems consider the historic average cost per gigabyte of RAM on a computer.
| Year | 5-Year Change ($) |
{: valign=”top”}|———-
| 1980 | 0 |
{: valign=”top”}| 1985 | −5,468,750 |
{: valign=”top”}| 1990 | −755,495 |
{: valign=”top”}| 1995 | −73,005 |
{: valign=”top”}| 2000 | −29,768 |
{: valign=”top”}| 2005 | −918 |
{: valign=”top”}| 2010 | −177 |
{: valign=”top”}{: .unnumbered summary=”A table with two columns and eight rows. The first column has the label “Year” and the values 1980, 1985, 1990, 1995, 2000, 2005, and 2010. The second column has the label “5-Tear Change ($)” and the values 0, -5,468,750, -755,495, -73,005, -29,768, -918, and -177.” data-label=””}
If the average cost per gigabyte of RAM in 2010 is $12, find the average cost per gigabyte of RAM in 1980.
The average cost per gigabyte of RAM can be approximated by the function
where
is measured in years since 1980, and
is cost in US$. Find the average cost per gigabyte of RAM for 1980 to 2010.
Find the average cost of 1GB RAM for 2005 to 2010.
The velocity of a bullet from a rifle can be approximated by
where
is seconds after the shot and
is the velocity measured in feet per second. This equation only models the velocity for the first half-second after the shot:
What is the total distance the bullet travels in 0.5 sec?
What is the average velocity of the bullet for the first half-second?

This work is licensed under a Creative Commons Attribution 4.0 International License.
You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution:

![Two graphs. The first shows the function f(x) = cos(x) / (4 + sin(x)^2). It is an oscillating function over [-6, 6] with turning points at roughly (-3, -2.5), (0, .25), and (3, -2.5), where (0,.25) is a local max and the others are local mins. The second shows the function F(x) = .5 * arctan(.5*sin(x)), which also oscillates over [-6,6]. It has turning points at roughly (-4.5, .25), (-1.5, -.25), (1.5, .25), and (4.5, -.25).](../resources/CNX_Calc_Figure_05_07_203.jpg)

![The graph of f(x) = arctan(x sin(x)) over [-6,6]. It has five turning points at roughly (-5, -1.5), (-2,1), (0,0), (2,1), and (5,-1.5).](../resources/CNX_Calc_Figure_05_07_207.jpg)
![A graph of the function f(x) = arctan(ln(x)) over (0, 2]. It is an increasing curve with x-intercept at (1,0).](../resources/CNX_Calc_Figure_05_07_209.jpg)

