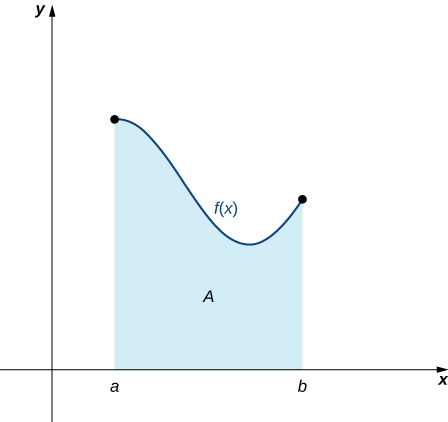
Archimedes was fascinated with calculating the areas of various shapes—in other words, the amount of space enclosed by the shape. He used a process that has come to be known as the method of exhaustion, which used smaller and smaller shapes, the areas of which could be calculated exactly, to fill an irregular region and thereby obtain closer and closer approximations to the total area. In this process, an area bounded by curves is filled with rectangles, triangles, and shapes with exact area formulas. These areas are then summed to approximate the area of the curved region.
In this section, we develop techniques to approximate the area between a curve, defined by a function
and the x-axis on a closed interval
Like Archimedes, we first approximate the area under the curve using shapes of known area (namely, rectangles). By using smaller and smaller rectangles, we get closer and closer approximations to the area. Taking a limit allows us to calculate the exact area under the curve.
Let’s start by introducing some notation to make the calculations easier. We then consider the case when
is continuous and nonnegative. Later in the chapter, we relax some of these restrictions and develop techniques that apply in more general cases.
As mentioned, we will use shapes of known area to approximate the area of an irregular region bounded by curves. This process often requires adding up long strings of numbers. To make it easier to write down these lengthy sums, we look at some new notation here, called sigma notation (also known as summation notation). The Greek capital letter
sigma, is used to express long sums of values in a compact form. For example, if we want to add all the integers from 1 to 20 without sigma notation, we have to write
We could probably skip writing a couple of terms and write
which is better, but still cumbersome. With sigma notation, we write this sum as
which is much more compact.
Typically, sigma notation is presented in the form
where
describes the terms to be added, and the i is called the index. Each term is evaluated, then we sum all the values, beginning with the value when
and ending with the value when
For example, an expression like
is interpreted as
Note that the index is used only to keep track of the terms to be added; it does not factor into the calculation of the sum itself. The index is therefore called a dummy variable. We can use any letter we like for the index. Typically, mathematicians use i, j, k, m, and n for indices.
Let’s try a couple of examples of using sigma notation.
for
Write in sigma notation and evaluate the sum of terms 2i for
Use the solving steps in [link] as a guide.
The properties associated with the summation process are given in the following rule.
Let
and
represent two sequences of terms and let c be a constant. The following properties hold for all positive integers n and for integers m, with
We prove properties 2. and 3. here, and leave proof of the other properties to the Exercises.
2. We have
3. We have
□
A few more formulas for frequently found functions simplify the summation process further. These are shown in the next rule, for sums and powers of integers, and we use them in the next set of examples.
Write using sigma notation and evaluate:
for
for
we can break the expression into three terms.
Find the sum of the values of
for
15,550
Use the properties of sigma notation to solve the problem.
Find the sum of the values of
over the integers
Using the formula, we have
Evaluate the sum indicated by the notation
440
Use the rule on sum and powers of integers.
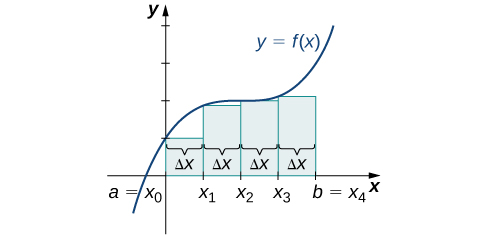
Now that we have the necessary notation, we return to the problem at hand: approximating the area under a curve. Let
be a continuous, nonnegative function defined on the closed interval
We want to approximate the area A bounded by
above, the x-axis below, the line
on the left, and the line
on the right ([link]).

How do we approximate the area under this curve? The approach is a geometric one. By dividing a region into many small shapes that have known area formulas, we can sum these areas and obtain a reasonable estimate of the true area. We begin by dividing the interval
into n subintervals of equal width,
We do this by selecting equally spaced points
with
and
for
We denote the width of each subinterval with the notation Δx, so
and
for
This notion of dividing an interval
into subintervals by selecting points from within the interval is used quite often in approximating the area under a curve, so let’s define some relevant terminology.
A set of points
for
with
which divides the interval
into subintervals of the form
is called a partition of
If the subintervals all have the same width, the set of points forms a regular partition of the interval
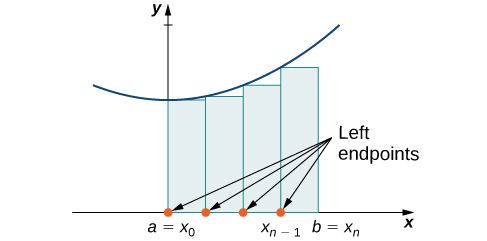
We can use this regular partition as the basis of a method for estimating the area under the curve. We next examine two methods: the left-endpoint approximation and the right-endpoint approximation.
On each subinterval
(for
construct a rectangle with width Δx and height equal to
which is the function value at the left endpoint of the subinterval. Then the area of this rectangle is
Adding the areas of all these rectangles, we get an approximate value for A ([link]). We use the notation Ln to denote that this is a left-endpoint approximation of A using n subintervals.
The second method for approximating area under a curve is the right-endpoint approximation. It is almost the same as the left-endpoint approximation, but now the heights of the rectangles are determined by the function values at the right of each subinterval.
Construct a rectangle on each subinterval
only this time the height of the rectangle is determined by the function value
at the right endpoint of the subinterval. Then, the area of each rectangle is
and the approximation for A is given by
The notation
indicates this is a right-endpoint approximation for A ([link]).
![In the right-endpoint approximation of area under a curve, the height of each rectangle is determined by the function value at the right of each subinterval. Note that the right-endpoint approximation differs from the left-endpoint approximation in [link]. A diagram showing the right-endpoint approximation of area under a curve. Under a parabola with vertex on the y axis and above the x axis, rectangles are drawn between a=x0 on the origin and b = xn. The rectangles have endpoints at a=x0, x1, x2…x(n-1), and b = xn, spaced equally. The height of each rectangle is determined by the value of the given function at the right endpoint of the rectangle.](../resources/CNX_Calc_Figure_05_01_002.jpg)
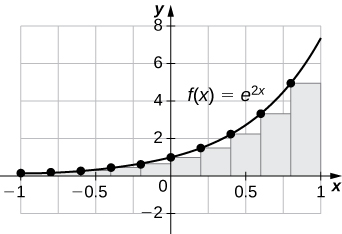
The graphs in [link] represent the curve
In graph (a) we divide the region represented by the interval
into six subintervals, each of width 0.5. Thus,
We then form six rectangles by drawing vertical lines perpendicular to
the left endpoint of each subinterval. We determine the height of each rectangle by calculating
for
The intervals are
We find the area of each rectangle by multiplying the height by the width. Then, the sum of the rectangular areas approximates the area between
and the x-axis. When the left endpoints are used to calculate height, we have a left-endpoint approximation. Thus,
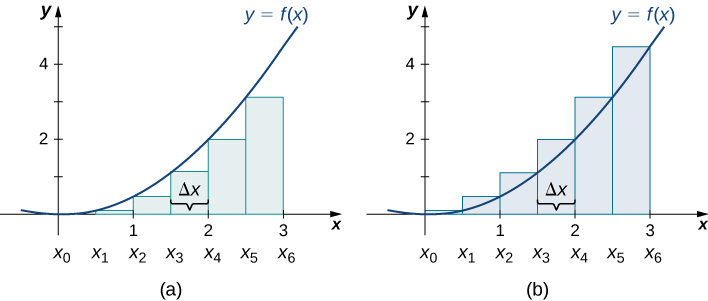
In [link](b), we draw vertical lines perpendicular to
such that
is the right endpoint of each subinterval, and calculate
for
We multiply each
by Δx to find the rectangular areas, and then add them. This is a right-endpoint approximation of the area under
Thus,
Use both left-endpoint and right-endpoint approximations to approximate the area under the curve of
on the interval
use
First, divide the interval
into n equal subintervals. Using
This is the width of each rectangle. The intervals
are shown in [link]. Using a left-endpoint approximation, the heights are
Then,
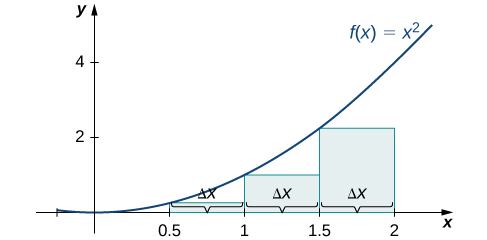
The right-endpoint approximation is shown in [link]. The intervals are the same,
but now use the right endpoint to calculate the height of the rectangles. We have
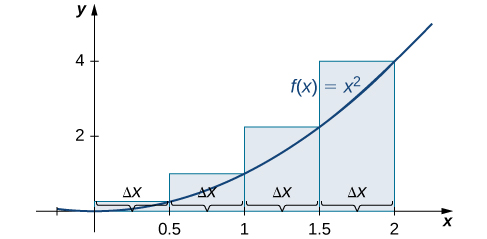
The left-endpoint approximation is 1.75; the right-endpoint approximation is 3.75.
Looking at [link] and the graphs in [link], we can see that when we use a small number of intervals, neither the left-endpoint approximation nor the right-endpoint approximation is a particularly accurate estimate of the area under the curve. However, it seems logical that if we increase the number of points in our partition, our estimate of A will improve. We will have more rectangles, but each rectangle will be thinner, so we will be able to fit the rectangles to the curve more precisely.
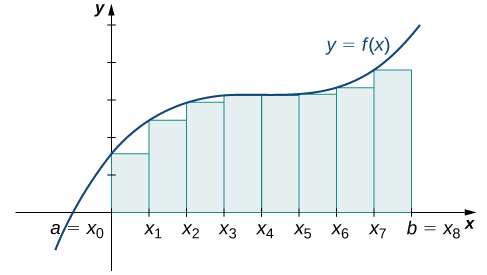
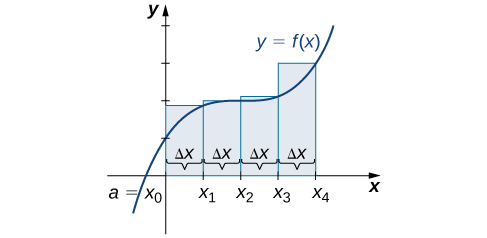
We can demonstrate the improved approximation obtained through smaller intervals with an example. Let’s explore the idea of increasing n, first in a left-endpoint approximation with four rectangles, then eight rectangles, and finally 32 rectangles. Then, let’s do the same thing in a right-endpoint approximation, using the same sets of intervals, of the same curved region. [link] shows the area of the region under the curve
on the interval
using a left-endpoint approximation where
The width of each rectangle is
The area is approximated by the summed areas of the rectangles, or
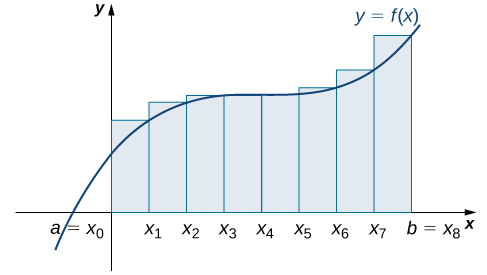
[link] shows the same curve divided into eight subintervals. Comparing the graph with four rectangles in [link] with this graph with eight rectangles, we can see there appears to be less white space under the curve when
This white space is area under the curve we are unable to include using our approximation. The area of the rectangles is
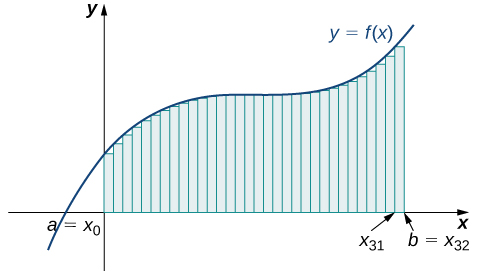
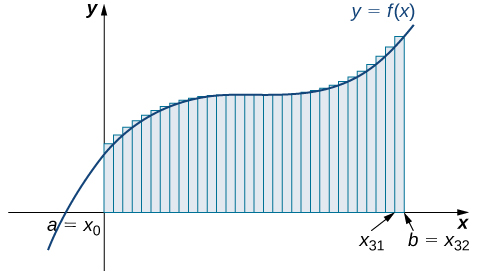
The graph in [link] shows the same function with 32 rectangles inscribed under the curve. There appears to be little white space left. The area occupied by the rectangles is
We can carry out a similar process for the right-endpoint approximation method. A right-endpoint approximation of the same curve, using four rectangles ([link]), yields an area
Dividing the region over the interval
into eight rectangles results in
The graph is shown in [link]. The area is
Last, the right-endpoint approximation with
is close to the actual area ([link]). The area is approximately
Based on these figures and calculations, it appears we are on the right track; the rectangles appear to approximate the area under the curve better as n gets larger. Furthermore, as n increases, both the left-endpoint and right-endpoint approximations appear to approach an area of 8 square units. [link] shows a numerical comparison of the left- and right-endpoint methods. The idea that the approximations of the area under the curve get better and better as n gets larger and larger is very important, and we now explore this idea in more detail.
| Values of n | Approximate Area Ln | Approximate Area Rn |
|---|---|---|
| 7.5 | 8.5 | |
| 7.75 | 8.25 | |
| 7.94 | 8.06 |
So far we have been using rectangles to approximate the area under a curve. The heights of these rectangles have been determined by evaluating the function at either the right or left endpoints of the subinterval
In reality, there is no reason to restrict evaluation of the function to one of these two points only. We could evaluate the function at any point ci in the subinterval
and use
as the height of our rectangle. This gives us an estimate for the area of the form
A sum of this form is called a Riemann sum, named for the 19th-century mathematician Bernhard Riemann, who developed the idea.
Let
be defined on a closed interval
and let P be a regular partition of
Let Δx be the width of each subinterval
and for each i, let
be any point in
A Riemann sum is defined for
as
Recall that with the left- and right-endpoint approximations, the estimates seem to get better and better as n get larger and larger. The same thing happens with Riemann sums. Riemann sums give better approximations for larger values of n. We are now ready to define the area under a curve in terms of Riemann sums.
Let
be a continuous, nonnegative function on an interval
and let
be a Riemann sum for
Then, the area under the curve
on
is given by
See a graphical demonstration of the construction of a Riemann sum.
Some subtleties here are worth discussing. First, note that taking the limit of a sum is a little different from taking the limit of a function
as x goes to infinity. Limits of sums are discussed in detail in the chapter on Sequences and Series; however, for now we can assume that the computational techniques we used to compute limits of functions can also be used to calculate limits of sums.
Second, we must consider what to do if the expression converges to different limits for different choices of
Fortunately, this does not happen. Although the proof is beyond the scope of this text, it can be shown that if
is continuous on the closed interval
then
exists and is unique (in other words, it does not depend on the choice of
We look at some examples shortly. But, before we do, let’s take a moment and talk about some specific choices for
Although any choice for
gives us an estimate of the area under the curve, we don’t necessarily know whether that estimate is too high (overestimate) or too low (underestimate). If it is important to know whether our estimate is high or low, we can select our value for
to guarantee one result or the other.
If we want an overestimate, for example, we can choose
such that for
for all
In other words, we choose
so that for
is the maximum function value on the interval
If we select
in this way, then the Riemann sum
is called an upper sum. Similarly, if we want an underestimate, we can choose
so that for
is the minimum function value on the interval
In this case, the associated Riemann sum is called a lower sum. Note that if
is either increasing or decreasing throughout the interval
then the maximum and minimum values of the function occur at the endpoints of the subintervals, so the upper and lower sums are just the same as the left- and right-endpoint approximations.
Find a lower sum for
on
let
subintervals.
With
over the interval
We can list the intervals as
Because the function is decreasing over the interval
[link] shows that a lower sum is obtained by using the right endpoints.
![The graph of f(x)=10−x2 is set up for a right-endpoint approximation of the area bounded by the curve and the x-axis on [1,2], and it shows a lower sum. The graph of f(x) = 10 − x^2 from 0 to 2. It is set up for a right-end approximation of the area bounded by the curve and the x axis on [1, 2], labeled a=x0 to x4. It shows a lower sum.](../resources/CNX_Calc_Figure_05_01_014.jpg)
The Riemann sum is
The area of 7.28 is a lower sum and an underestimate.
on
let
![A graph of the function f(x) = 10 − x^2 from 0 to 2. It is set up for a right endpoint approximation over the area [1,2], which is labeled a=x0 to x4. It is an upper sum.](../resources/CNX_Calc_Figure_05_01_015.jpg)
is decreasing on
so the maximum function values occur at the left endpoints of the subintervals.
Find a lower sum for
over the interval
let
Let’s first look at the graph in [link] to get a better idea of the area of interest.
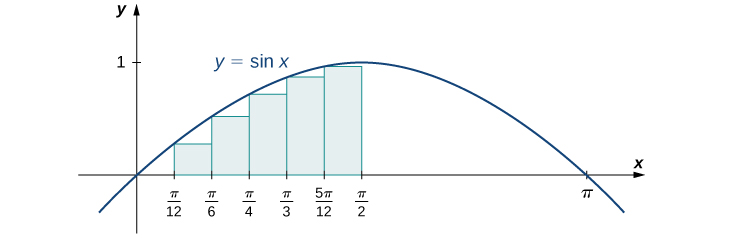
The intervals are
and
Note that
is increasing on the interval
so a left-endpoint approximation gives us the lower sum. A left-endpoint approximation is the Riemann sum
We have
is useful for expressing long sums of values in compact form.
the process of dividing the interval into n equal parts, extending a rectangle to the graph of the function, calculating the areas of the series of rectangles, and then summing the areas yields an approximation of the area of that region.
and can be used to estimate the area under the curve
Left- and right-endpoint approximations are special kinds of Riemann sums where the values of
are chosen to be the left or right endpoints of the subintervals, respectively.
at which the function is evaluated, often with an eye to obtaining a lower sum or an upper sum.
State whether the given sums are equal or unequal.
and
and
and
and
a. They are equal; both represent the sum of the first 10 whole numbers. b. They are equal; both represent the sum of the first 10 whole numbers. c. They are equal by substituting
d. They are equal; the first sum factors the terms of the second.
In the following exercises, use the rules for sums of powers of integers to compute the sums.
Suppose that
and
In the following exercises, compute the sums.
In the following exercises, use summation properties and formulas to rewrite and evaluate the sums.
Let
denote the left-endpoint sum using n subintervals and let
denote the corresponding right-endpoint sum. In the following exercises, compute the indicated left and right sums for the given functions on the indicated interval.
L4 for
on
R4 for
on
L6 for
on
R6 for
on
R4 for
on
L4 for
on
R4 for
on
L8 for
on
Compute the left and right Riemann sums—L4 and R4, respectively—for
on
Compute their average value and compare it with the area under the graph of f.
Compute the left and right Riemann sums—L6 and R6, respectively—for
on
Compute their average value and compare it with the area under the graph of f.
The graph of f is a triangle with area 9.
Compute the left and right Riemann sums—L4 and R4, respectively—for
on
and compare their values.
Compute the left and right Riemann sums—L6 and R6, respectively—for
on
and compare their values.
They are equal.
Express the following endpoint sums in sigma notation but do not evaluate them.
L30 for
on
L10 for
on
R20 for
on
R100 for
on
In the following exercises, graph the function then use a calculator or a computer program to evaluate the following left and right endpoint sums. Is the area under the curve between the left and right endpoint sums?
[T] L100 and R100 for
on the interval
[T] L100 and R100 for
on the interval
![A graph of the given function on the interval [0, 1]. It is set up for a left endpoint approximation and is an underestimate because the function is increasing. Ten rectangles are shown for visual clarity, but this behavior persists for more rectangles.](../resources/CNX_Calc_Figure_05_01_207.jpg)
The plot shows that the left Riemann sum is an underestimate because the function is increasing. Similarly, the right Riemann sum is an overestimate. The area lies between the left and right Riemann sums. Ten rectangles are shown for visual clarity. This behavior persists for more rectangles.
[T] L50 and R50 for
on the interval
[T] L100 and R100 for
on the interval
![A graph of the given function over [-1,1] set up for a left endpoint approximation. It is an underestimate since the function is increasing. Ten rectangles are shown for visual clarity, but this behavior persists for more rectangles.](../resources/CNX_Calc_Figure_05_01_209.jpg)
The left endpoint sum is an underestimate because the function is increasing. Similarly, a right endpoint approximation is an overestimate. The area lies between the left and right endpoint estimates.
[T] L50 and R50 for
on the interval
[T] L100 and R100 for
on the interval
The plot shows that the left Riemann sum is an underestimate because the function is increasing. Ten rectangles are shown for visual clarity. This behavior persists for more rectangles.
Let tj denote the time that it took Tejay van Garteren to ride the jth stage of the Tour de France in 2014. If there were a total of 21 stages, interpret
Let
denote the total rainfall in Portland on the jth day of the year in 2009. Interpret
The sum represents the cumulative rainfall in January 2009.
Let
denote the hours of daylight and
denote the increase in the hours of daylight from day
to day j in Fargo, North Dakota, on the jth day of the year. Interpret
To help get in shape, Joe gets a new pair of running shoes. If Joe runs 1 mi each day in week 1 and adds
mi to his daily routine each week, what is the total mileage on Joe’s shoes after 25 weeks?
The total mileage is
The following table gives approximate values of the average annual atmospheric rate of increase in carbon dioxide (CO2) each decade since 1960, in parts per million (ppm). Estimate the total increase in atmospheric CO2 between 1964 and 2013.
| Decade | Ppm/y |
|---|---|
| 1964–1973 | 1.07 |
| 1974–1983 | 1.34 |
| 1984–1993 | 1.40 |
| 1994–2003 | 1.87 |
| 2004–2013 | 2.07 |
The following table gives the approximate increase in sea level in inches over 20 years starting in the given year. Estimate the net change in mean sea level from 1870 to 2010.
| Starting Year | 20-Year Change |
|---|---|
| 1870 | 0.3 |
| 1890 | 1.5 |
| 1910 | 0.2 |
| 1930 | 2.8 |
| 1950 | 0.7 |
| 1970 | 1.1 |
| 1990 | 1.5 |
Add the numbers to get 8.1-in. net increase.
The following table gives the approximate increase in dollars in the average price of a gallon of gas per decade since 1950. If the average price of a gallon of gas in 2010 was $2.60, what was the average price of a gallon of gas in 1950?
| Starting Year | 10-Year Change |
|---|---|
| 1950 | 0.03 |
| 1960 | 0.05 |
| 1970 | 0.86 |
| 1980 | −0.03 |
| 1990 | 0.29 |
| 2000 | 1.12 |
The following table gives the percent growth of the U.S. population beginning in July of the year indicated. If the U.S. population was 281,421,906 in July 2000, estimate the U.S. population in July 2010.
| Year | % Change/Year |
|---|---|
| 2000 | 1.12 |
| 2001 | 0.99 |
| 2002 | 0.93 |
| 2003 | 0.86 |
| 2004 | 0.93 |
| 2005 | 0.93 |
| 2006 | 0.97 |
| 2007 | 0.96 |
| 2008 | 0.95 |
| 2009 | 0.88 |
(Hint: To obtain the population in July 2001, multiply the population in July 2000 by 1.0112 to get 284,573,831.)
309,389,957
In the following exercises, estimate the areas under the curves by computing the left Riemann sums, L8.
[T] Use a computer algebra system to compute the Riemann sum,
for
for
on
[T] Use a computer algebra system to compute the Riemann sum, LN, for
for
on
[T] Use a computer algebra system to compute the Riemann sum, LN, for
for
on
Compare these estimates with π.
In the following exercises, use a calculator or a computer program to evaluate the endpoint sums RN and LN for
How do these estimates compare with the exact answers, which you can find via geometry?
[T]
on the interval
and
By symmetry of the graph, the exact area is zero.
[T]
on the interval
In the following exercises, use a calculator or a computer program to evaluate the endpoint sums RN and LN for
[T]
on the interval
which has an exact area of
[T]
on the interval
which has an exact area of
Explain why, if
and f is increasing on
that the left endpoint estimate is a lower bound for the area below the graph of f on
If
is a subinterval of
under one of the left-endpoint sum rectangles, then the area of the rectangle contributing to the left-endpoint estimate is
But,
for
so the area under the graph of f between c and d is
plus the area below the graph of f but above the horizontal line segment at height
which is positive. As this is true for each left-endpoint sum interval, it follows that the left Riemann sum is less than or equal to the area below the graph of f on
Explain why, if
and f is decreasing on
that the left endpoint estimate is an upper bound for the area below the graph of f on
Show that, in general,
and
The left sum has a term corresponding to
and the right sum has a term corresponding to
In
any term corresponding to
occurs once with a plus sign and once with a minus sign, so each such term cancels and one is left with
Explain why, if f is increasing on
the error between either LN or RN and the area A below the graph of f is at most
For each of the three graphs:
for the area enclosed by the curve by adding the areas of the squares enclosed completely by the curve.
for the area by adding to
the areas
of the squares enclosed partially by the curve.
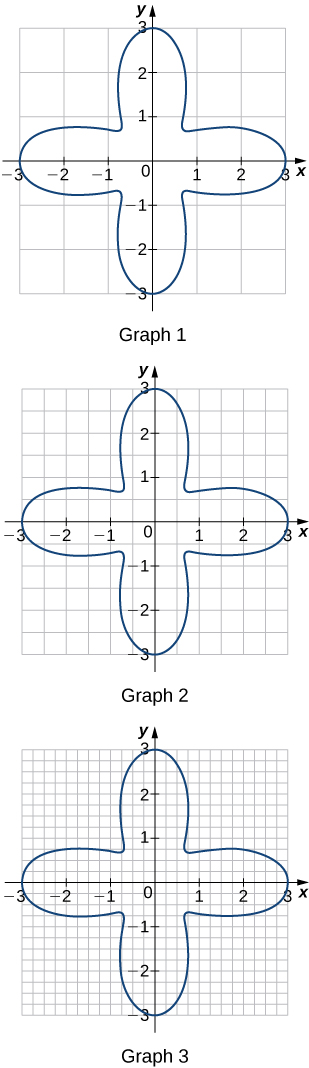
Graph 1: a.
b.
Graph 2: a.
b.
Graph 3: a.
b.
In the previous exercise, explain why
gets no smaller while
gets no larger as the squares are subdivided into four boxes of equal area.
A unit circle is made up of n wedges equivalent to the inner wedge in the figure. The base of the inner triangle is 1 unit and its height is
The base of the outer triangle is
and the height is
Use this information to argue that the area of a unit circle is equal to π.
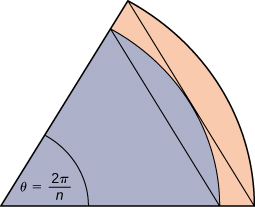
Let A be the area of the unit circle. The circle encloses n congruent triangles each of area
so
Similarly, the circle is contained inside n congruent triangles each of area
so
As
so we conclude
Also, as
so we also have
By the squeeze theorem for limits, we conclude that
on each subinterval
on each subinterval

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: