At this point, we have seen how to calculate derivatives of many functions and have been introduced to a variety of their applications. We now ask a question that turns this process around: Given a function
how do we find a function with the derivative
and why would we be interested in such a function?
We answer the first part of this question by defining antiderivatives. The antiderivative of a function
is a function with a derivative
Why are we interested in antiderivatives? The need for antiderivatives arises in many situations, and we look at various examples throughout the remainder of the text. Here we examine one specific example that involves rectilinear motion. In our examination in Derivatives of rectilinear motion, we showed that given a position function
of an object, then its velocity function
is the derivative of
—that is,
Furthermore, the acceleration
is the derivative of the velocity
—that is,
Now suppose we are given an acceleration function
but not the velocity function
or the position function
Since
determining the velocity function requires us to find an antiderivative of the acceleration function. Then, since
determining the position function requires us to find an antiderivative of the velocity function. Rectilinear motion is just one case in which the need for antiderivatives arises. We will see many more examples throughout the remainder of the text. For now, let’s look at the terminology and notation for antiderivatives, and determine the antiderivatives for several types of functions. We examine various techniques for finding antiderivatives of more complicated functions later in the text (Introduction to Techniques of Integration).
At this point, we know how to find derivatives of various functions. We now ask the opposite question. Given a function
how can we find a function with derivative
If we can find a function
derivative
we call
an antiderivative of
A function
is an antiderivative of the function
if
for all
in the domain of
Consider the function
Knowing the power rule of differentiation, we conclude that
is an antiderivative of
since
Are there any other antiderivatives of
Yes; since the derivative of any constant
is zero,
is also an antiderivative of
Therefore,
and
are also antiderivatives. Are there any others that are not of the form
for some constant
The answer is no. From Corollary
of the Mean Value Theorem, we know that if
and
are differentiable functions such that
then
for some constant
This fact leads to the following important theorem.
Let
be an antiderivative of
over an interval
Then,
the function
is also an antiderivative of
over
is an antiderivative of
over
there is a constant
for which
over
In other words, the most general form of the antiderivative of
over
is
We use this fact and our knowledge of derivatives to find all the antiderivatives for several functions.
For each of the following functions, find all antiderivatives.
then
is an antiderivative of
Therefore, every antiderivative of
is of the form
for some constant
and every function of the form
is an antiderivative of
For
and
For
and
Therefore,
Thus,
is an antiderivative of
Therefore, every antiderivative of
is of the form
for some constant
and every function of the form
is an antiderivative of
so
is an antiderivative of
Therefore, every antiderivative of
is of the form
for some constant
and every function of the form
is an antiderivative of
then
is an antiderivative of
Therefore, every antiderivative of
is of the form
for some constant
and every function of the form
is an antiderivative of
Find all antiderivatives of
What function has a derivative of
We now look at the formal notation used to represent antiderivatives and examine some of their properties. These properties allow us to find antiderivatives of more complicated functions. Given a function
we use the notation
or
to denote the derivative of
Here we introduce notation for antiderivatives. If
is an antiderivative of
we say that
is the most general antiderivative of
and write
The symbol
is called an integral sign, and
is called the indefinite integral of
Given a function
the indefinite integral of
denoted
is the most general antiderivative of
If
is an antiderivative of
then
The expression
is called the integrand and the variable
is the variable of integration.
Given the terminology introduced in this definition, the act of finding the antiderivatives of a function
is usually referred to as integrating
For a function
and an antiderivative
the functions
where
is any real number, is often referred to as the family of antiderivatives of
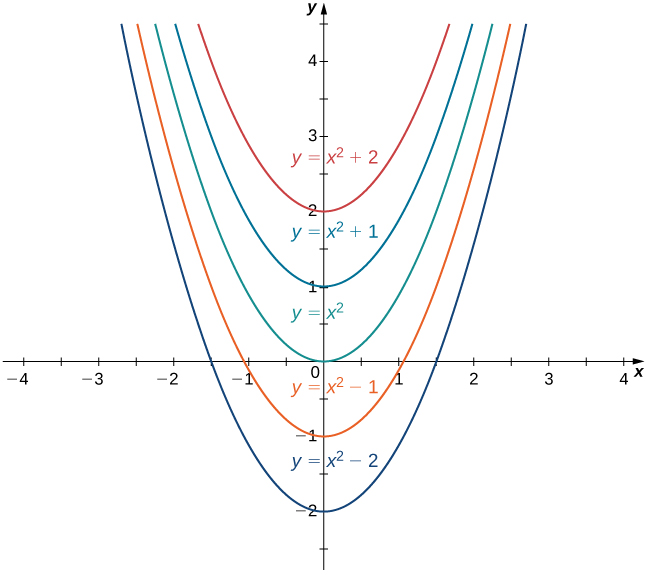
For example, since
is an antiderivative of
and any antiderivative of
is of the form
we write
The collection of all functions of the form
where
is any real number, is known as the family of antiderivatives of
[link] shows a graph of this family of antiderivatives.

For some functions, evaluating indefinite integrals follows directly from properties of derivatives. For example, for
which comes directly from
This fact is known as the power rule for integrals.
For
Evaluating indefinite integrals for some other functions is also a straightforward calculation. The following table lists the indefinite integrals for several common functions. A more complete list appears in Appendix B.
| Differentiation Formula | Indefinite Integral |
|---|---|
| for | |
From the definition of indefinite integral of
we know
if and only if
is an antiderivative of
Therefore, when claiming that
it is important to check whether this statement is correct by verifying that
Each of the following statements is of the form
Verify that each statement is correct by showing that
the statement
is correct.
Note that we are verifying an indefinite integral for a sum. Furthermore,
and
are antiderivatives of
and
respectively, and the sum of the antiderivatives is an antiderivative of the sum. We discuss this fact again later in this section.
Therefore, the statement
is correct.
Note that we are verifying an indefinite integral for a product. The antiderivative
is not a product of the antiderivatives. Furthermore, the product of antiderivatives,
is not an antiderivative of
since
In general, the product of antiderivatives is not an antiderivative of a product.
Verify that
Calculate
In [link], we listed the indefinite integrals for many elementary functions. Let’s now turn our attention to evaluating indefinite integrals for more complicated functions. For example, consider finding an antiderivative of a sum
In [link]a. we showed that an antiderivative of the sum
is given by the sum
—that is, an antiderivative of a sum is given by a sum of antiderivatives. This result was not specific to this example. In general, if
and
are antiderivatives of any functions
and
respectively, then
Therefore,
is an antiderivative of
and we have
Similarly,
In addition, consider the task of finding an antiderivative of
where
is any real number. Since
for any real number
we conclude that
These properties are summarized next.
Let
and
be antiderivatives of
and
respectively, and let
be any real number.
Sums and Differences
Constant Multiples
From this theorem, we can evaluate any integral involving a sum, difference, or constant multiple of functions with antiderivatives that are known. Evaluating integrals involving products, quotients, or compositions is more complicated (see [link]b. for an example involving an antiderivative of a product.) We look at and address integrals involving these more complicated functions in Introduction to Integration. In the next example, we examine how to use this theorem to calculate the indefinite integrals of several functions.
Evaluate each of the following indefinite integrals:
From the second part of [link], each coefficient can be written in front of the integral sign, which gives
Using the power rule for integrals, we conclude that
Then, to evaluate the integral, integrate each of these terms separately. Using the power rule, we have
Then, use the fact that
is an antiderivative of
to conclude that
Therefore,
Evaluate
Integrate each term in the integrand separately, making use of the power rule.
We look at techniques for integrating a large variety of functions involving products, quotients, and compositions later in the text. Here we turn to one common use for antiderivatives that arises often in many applications: solving differential equations.
A differential equation is an equation that relates an unknown function and one or more of its derivatives. The equation
is a simple example of a differential equation. Solving this equation means finding a function
with a derivative
Therefore, the solutions of [link] are the antiderivatives of
If
is one antiderivative of
every function of the form
is a solution of that differential equation. For example, the solutions of
are given by
Sometimes we are interested in determining whether a particular solution curve passes through a certain point
—that is,
The problem of finding a function
that satisfies a differential equation
with the additional condition
is an example of an initial-value problem. The condition
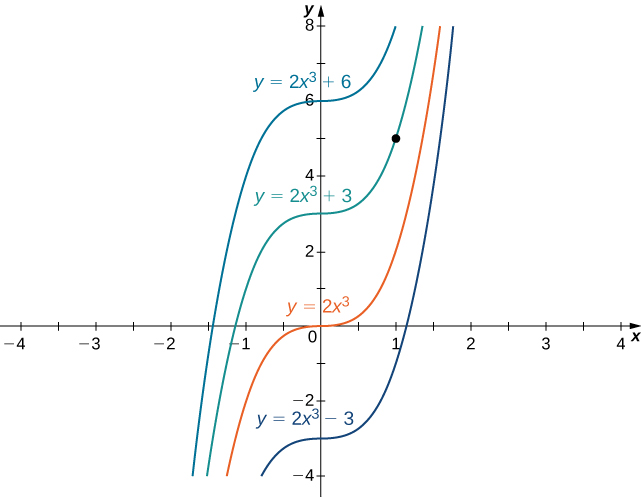
is known as an initial condition. For example, looking for a function
that satisfies the differential equation
and the initial condition
is an example of an initial-value problem. Since the solutions of the differential equation are
to find a function
that also satisfies the initial condition, we need to find
such that
From this equation, we see that
and we conclude that
is the solution of this initial-value problem as shown in the following graph.
Solve the initial-value problem
First we need to solve the differential equation. If
then
Next we need to look for a solution
that satisfies the initial condition. The initial condition
means we need a constant
such that
Therefore,
The solution of the initial-value problem is
Solve the initial value problem
Find all antiderivatives of
Initial-value problems arise in many applications. Next we consider a problem in which a driver applies the brakes in a car. We are interested in how long it takes for the car to stop. Recall that the velocity function
is the derivative of a position function
and the acceleration
is the derivative of the velocity function. In earlier examples in the text, we could calculate the velocity from the position and then compute the acceleration from the velocity. In the next example we work the other way around. Given an acceleration function, we calculate the velocity function. We then use the velocity function to determine the position function.
A car is traveling at the rate of
ft/sec
mph) when the brakes are applied. The car begins decelerating at a constant rate of
ft/sec2.
be the time (in seconds) after the brakes are first applied. Let
be the acceleration of the car (in feet per seconds squared) at time
Let
be the velocity of the car (in feet per second) at time
Let
be the car’s position (in feet) beyond the point where the brakes are applied at time
The car is traveling at a rate of
Therefore, the initial velocity is
ft/sec. Since the car is decelerating, the acceleration is
The acceleration is the derivative of the velocity,
Therefore, we have an initial-value problem to solve:
Integrating, we find that
Since
Thus, the velocity function is
To find how long it takes for the car to stop, we need to find the time
such that the velocity is zero. Solving
we obtain
sec.
sec. We know the velocity
is the derivative of the position
Consider the initial position to be
Therefore, we need to solve the initial-value problem
Integrating, we have
Since
the constant is
Therefore, the position function is
After
sec, the position is
ft.
Suppose the car is traveling at the rate of
ft/sec. How long does it take for the car to stop? How far will the car travel?
is an antiderivative of
then every antiderivative of
is of the form
for some constant
requires us first to find the set of antiderivatives of
and then to look for the particular antiderivative that also satisfies the initial condition.
For the following exercises, show that
are antiderivatives of
For the following exercises, find the antiderivative of the function.
For the following exercises, find the antiderivative
of each function
For the following exercises, evaluate the integral.
For the following exercises, solve the initial value problem.
For the following exercises, find two possible functions
given the second- or third-order derivatives.
Answers may vary; one possible answer is
Answers may vary; one possible answer is
A car is being driven at a rate of
mph when the brakes are applied. The car decelerates at a constant rate of
ft/sec2. How long before the car stops?
sec
In the preceding problem, calculate how far the car travels in the time it takes to stop.
You are merging onto the freeway, accelerating at a constant rate of
ft/sec2. How long does it take you to reach merging speed at
mph?
sec
Based on the previous problem, how far does the car travel to reach merging speed?
A car company wants to ensure its newest model can stop in
sec when traveling at
mph. If we assume constant deceleration, find the value of deceleration that accomplishes this.
ft/sec2
A car company wants to ensure its newest model can stop in less than
ft when traveling at
mph. If we assume constant deceleration, find the value of deceleration that accomplishes this.
For the following exercises, find the antiderivative of the function, assuming
[T]
[T]
[T]
[T]
[T]
[T]
For the following exercises, determine whether the statement is true or false. Either prove it is true or find a counterexample if it is false.
If
is the antiderivative of
then
is the antiderivative of
True
If
is the antiderivative of
then
is the antiderivative of
If
is the antiderivative of
then
is the antiderivative of
False
If
is the antiderivative of
then
is the antiderivative of
True or False? Justify your answer with a proof or a counterexample. Assume that
is continuous and differentiable unless stated otherwise.
If
and
then there exists at least one point
such that
True, by Mean Value Theorem
If
there is a maximum or minimum at
There is a function such that
and
(A graphical “proof” is acceptable for this answer.)
True
There is a function such that there is both an inflection point and a critical point for some value
Given the graph of
determine where
is increasing or decreasing.
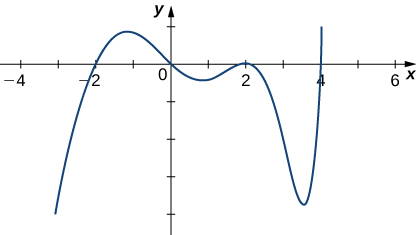
Increasing:
decreasing:
The graph of
is given below. Draw
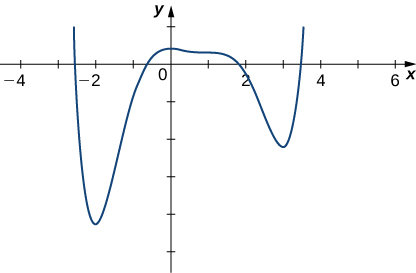
Find the linear approximation
to
near
Find the differential of
and evaluate for
with
Find the critical points and the local and absolute extrema of the following functions on the given interval.
over
Critical point:
absolute minimum:
absolute maximum:
over
Determine over which intervals the following functions are increasing, decreasing, concave up, and concave down.
Increasing:
decreasing:
concave up:
concave down:
Increasing:
decreasing:
concave up:
concave down: nowhere
Evaluate the following limits.
Use Newton’s method to find the first two iterations, given the starting point.
Find the antiderivatives
of the following functions.
Graph the following functions by hand. Make sure to label the inflection points, critical points, zeros, and asymptotes.
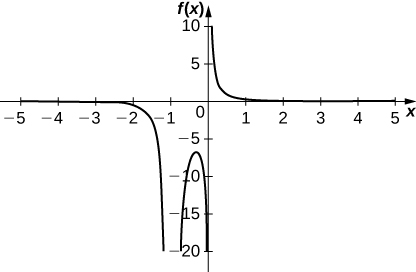
Inflection points: none; critical points:
zeros: none; vertical asymptotes:
horizontal asymptote:
A car is being compacted into a rectangular solid. The volume is decreasing at a rate of
m3/sec. The length and width of the compactor are square, but the height is not the same length as the length and width. If the length and width walls move toward each other at a rate of
m/sec, find the rate at which the height is changing when the length and width are
m and the height is
m.
The height is decreasing at a rate of
m/sec
A rocket is launched into space; its kinetic energy is given by
where
is the kinetic energy in joules,
is the mass of the rocket in kilograms, and
is the velocity of the rocket in meters/second. Assume the velocity is increasing at a rate of
m/sec2 and the mass is decreasing at a rate of
kg/sec because the fuel is being burned. At what rate is the rocket’s kinetic energy changing when the mass is
kg and the velocity is
m/sec? Give your answer in mega-Joules (MJ), which is equivalent to
J.
The famous Regiomontanus’ problem for angle maximization was proposed during the
th century. A painting hangs on a wall with the bottom of the painting a distance
feet above eye level, and the top
feet above eye level. What distance
(in feet) from the wall should the viewer stand to maximize the angle subtended by the painting,
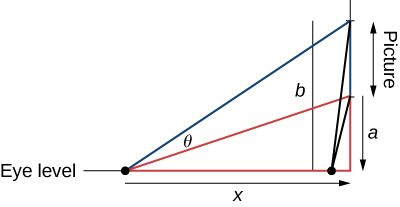
feet
An airline sells tickets from Tokyo to Detroit for
There are
seats available and a typical flight books
seats. For every
decrease in price, the airline observes an additional five seats sold. What should the fare be to maximize profit? How many passengers would be onboard?
such that
for all
in the domain of
is an antiderivative of
is the indefinite integral of
we use the notation
to denote the indefinite integral of
that satisfies the differential equation
together with the initial condition

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: