Newton’s Method

In many areas of pure and applied mathematics, we are interested in finding solutions to an equation of the form f(x)=0.

For most functions, however, it is difficult—if not impossible—to calculate their zeroes explicitly. In this section, we take a look at a technique that provides a very efficient way of approximating the zeroes of functions. This technique makes use of tangent line approximations and is behind the method used often by calculators and computers to find zeroes.

Describing Newton’s Method

Consider the task of finding the solutions of f(x)=0.

If f

is the first-degree polynomial f(x)=ax+b,

then the solution of f(x)=0

is given by the formula x=−ba.

If f

is the second-degree polynomial f(x)=ax2+bx+c,

the solutions of f(x)=0

can be found by using the quadratic formula. However, for polynomials of degree 3

or more, finding roots of f

becomes more complicated. Although formulas exist for third- and fourth-degree polynomials, they are quite complicated. Also, if f

is a polynomial of degree 5

or greater, it is known that no such formulas exist. For example, consider the function

f(x)=x5+8x4+4x3−2x−7.

No formula exists that allows us to find the solutions of f(x)=0.

Similar difficulties exist for nonpolynomial functions. For example, consider the task of finding solutions of tan(x)−x=0.

No simple formula exists for the solutions of this equation. In cases such as these, we can use Newton’s method to approximate the roots.

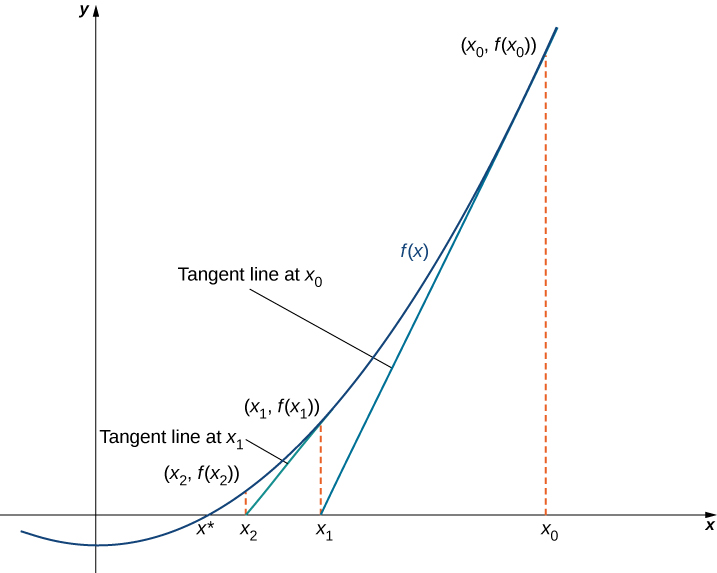
Newton’s method makes use of the following idea to approximate the solutions of f(x)=0.

By sketching a graph of f,

we can estimate a root of f(x)=0.

Let’s call this estimate x0.

We then draw the tangent line to f

at x0.

If f′(x0)≠0,

this tangent line intersects the x

-axis at some point (x1,0).

Now let x1

be the next approximation to the actual root. Typically, x1

is closer than x0

to an actual root. Next we draw the tangent line to f

at x1.

If f′(x1)≠0,

this tangent line also intersects the x

-axis, producing another approximation, x2.

We continue in this way, deriving a list of approximations: x0,x1,x2,….

Typically, the numbers x0,x1,x2,…

quickly approach an actual root x*,

as shown in the following figure.

This function f(x) is drawn with points (x0, f(x0)), (x1, f(x1)), and (x2, f(x2)) marked on the function. From (x0, f(x0)), a tangent line is drawn, and it strikes the x axis at x1. From (x0, f(x0)), a tangent line is drawn, and it strikes the x axis at x2. If a tangent line were drawn from (x2, f(x2)), it appears that it would come very close to x*, which is the actual root. Each tangent line drawn in this order appears to get closer and closer to x*.

Now let’s look at how to calculate the approximations x0,x1,x2,….

If x0

is our first approximation, the approximation x1

is defined by letting (x1,0)

be the x

-intercept of the tangent line to f

at x0.

The equation of this tangent line is given by

y=f(x0)+f′(x0)(x−x0).

Therefore, x1

must satisfy

f(x0)+f′(x0)(x1−x0)=0.

Solving this equation for x1,

we conclude that

x1=x0−f(x0)f′(x0).

Similarly, the point (x2,0)

is the x

-intercept of the tangent line to f

at x1.

Therefore, x2

satisfies the equation

x2=x1−f(x1)f′(x1).

In general, for n>0,xn

satisfies

xn=xn−1−f(xn−1)f′(xn−1).

Next we see how to make use of this technique to approximate the root of the polynomial f(x)=x3−3x+1.

Finding a Root of a Polynomial

Use Newton’s method to approximate a root of f(x)=x3−3x+1

in the interval [1,2].

Let x0=2

and find x1,x2,x3,x4,

and x5.

From [link], we see that f

has one root over the interval (1,2).

Therefore x0=2

seems like a reasonable first approximation. To find the next approximation, we use [link]. Since f(x)=x3−3x+1,

the derivative is f′(x)=3x2−3.

Using [link] with n=1

(and a calculator that displays 10

digits), we obtain

x1=x0−f(x0)f′(x0)=2−f(2)f′(2)=2−39≈1.666666667.

To find the next approximation, x2,

we use [link] with n=2

and the value of x1

stored on the calculator. We find that

x2=x1=f(x1)f′(x1)≈1.548611111.

Continuing in this way, we obtain the following results:

x1≈1.666666667x2≈1.548611111x3≈1.532390162x4≈1.532088989x5≈1.532088886x6≈1.532088886.

We note that we obtained the same value for x5

and x6.

Therefore, any subsequent application of Newton’s method will most likely give the same value for xn.

The function f(x) = x3 – 3x + 1 is drawn. It has roots between −2 and −1, 0 and 1, and 1 and 2.

Letting x0=0,

let’s use Newton’s method to approximate the root of f(x)=x3−3x+1

over the interval [0,1]

by calculating x1

and x2.

x1≈0.33333333,x2≈0.347222222
Hint

Use [link].

Newton’s method can also be used to approximate square roots. Here we show how to approximate 2.

This method can be modified to approximate the square root of any positive number.

Finding a Square Root

Use Newton’s method to approximate 2

([link]). Let f(x)=x2−2,

let x0=2,

and calculate x1,x2,x3,x4,x5.

(We note that since f(x)=x2−2

has a zero at 2,

the initial value x0=2

is a reasonable choice to approximate 2.)

For f(x)=x2−2,f′(x)=2x.

From [link], we know that

xn=xn−1−f(xn−1)f′(xn−1)=xn−1−x2n−1−22xn−1=12xn−1+1xn−1=12(xn−1+2xn−1).

Therefore,

x1=12(x0+2x0)=12(2+22)=1.5x2=12(x1+2x1)=12(1.5+21.5)≈1.416666667.

Continuing in this way, we find that

x1=1.5x2≈1.416666667x3≈1.414215686x4≈1.414213562x5≈1.414213562.

Since we obtained the same value for x4

and x5,

it is unlikely that the value xn

will change on any subsequent application of Newton’s method. We conclude that 2≈1.414213562.

The function y = x2 – 2 is drawn. A dashed line comes up from x0 = 2, and a tangent line is drawn down from there. It touches x1 = 1.5, which is near x* = the square root of 2.

Use Newton’s method to approximate 3

by letting f(x)=x2−3

and x0=3.

Find x1

and x2.

x1=2,x2=1.75
Hint

For f(x)=x2−3,

[link] reduces to xn=xn−12+32xn−1.

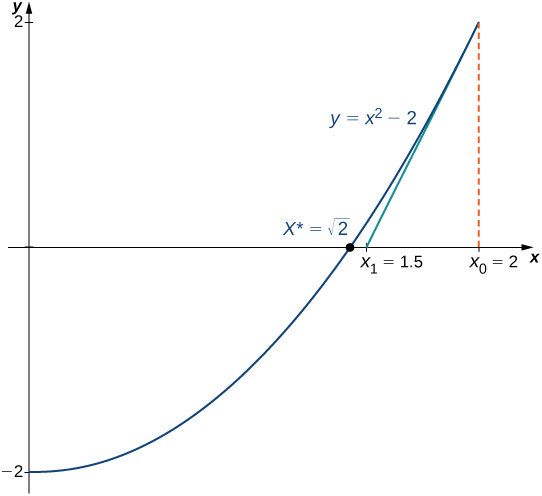
When using Newton’s method, each approximation after the initial guess is defined in terms of the previous approximation by using the same formula. In particular, by defining the function F(x)=x−[f(x)f′(x)],

we can rewrite [link] as xn=F(xn−1).

This type of process, where each xn

is defined in terms of xn−1

by repeating the same function, is an example of an iterative process. Shortly, we examine other iterative processes. First, let’s look at the reasons why Newton’s method could fail to find a root.

Failures of Newton’s Method

Typically, Newton’s method is used to find roots fairly quickly. However, things can go wrong. Some reasons why Newton’s method might fail include the following:

  1. At one of the approximations xn,

    the derivative

    f′

    is zero at

    xn,

    but

    f(xn)≠0.

    As a result, the tangent line of

    f

    at

    xn

    does not intersect the

    x

    -axis. Therefore, we cannot continue the iterative process.

  2. The approximations x0,x1,x2,…

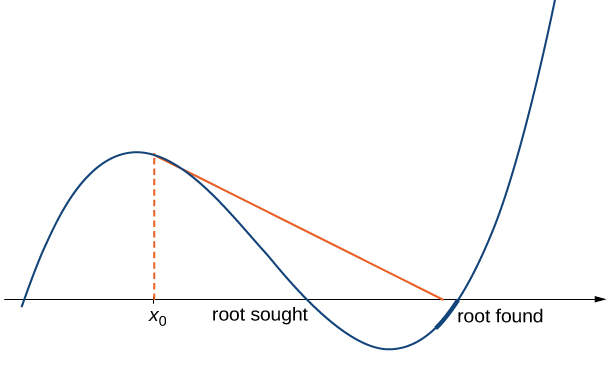
    may approach a different root. If the function

    f

    has more than one root, it is possible that our approximations do not approach the one for which we are looking, but approach a different root (see [link]). This event most often occurs when we do not choose the approximation

    x0

    close enough to the desired root.

  3. The approximations may fail to approach a root entirely. In [link], we provide an example of a function and an initial guess x0

    such that the successive approximations never approach a root because the successive approximations continue to alternate back and forth between two values.

A function is drawn with two roots, labeled root sought and root found. A point x0 is chosen such that when the tangent of x0 is taken, even though it is nearer to the root sought, the tangent points to the root found.

When Newton’s Method Fails

Consider the function f(x)=x3−2x+2.

Let x0=0.

Show that the sequence x1,x2,…

fails to approach a root of f.

For f(x)=x3−2x+2,

the derivative is f′(x)=3x2−2.

Therefore,

x1=x0−f(x0)f′(x0)=0−f(0)f′(0)=−2−2=1.

In the next step,

x2=x1−f(x1)f′(x1)=1−f(1)f′(1)=1−11=0.

Consequently, the numbers x0,x1,x2,…

continue to bounce back and forth between 0

and 1

and never get closer to the root of f

which is over the interval [−2,−1]

(see [link]). Fortunately, if we choose an initial approximation x0

closer to the actual root, we can avoid this situation.

The function f(x) = x3 – 2x + 2 is drawn, which has a root between −2 and −1. The tangent from x = 0 goes to x = 1, and the tangent from x = 1 goes to x = 0.

For f(x)=x3−2x+2,

let x0=−1.5

and find x1

and x2.

x1≈−1.842105263,x2≈−1.772826920
Hint

Use [link].

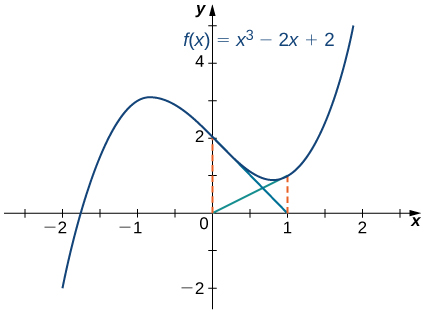
From [link], we see that Newton’s method does not always work. However, when it does work, the sequence of approximations approaches the root very quickly. Discussions of how quickly the sequence of approximations approach a root found using Newton’s method are included in texts on numerical analysis.

Other Iterative Processes

As mentioned earlier, Newton’s method is a type of iterative process. We now look at an example of a different type of iterative process.

Consider a function F

and an initial number x0.

Define the subsequent numbers xn

by the formula xn=F(xn−1).

This process is an iterative process that creates a list of numbers x0,x1,x2,…,xn,….

This list of numbers may approach a finite number x*

as n

gets larger, or it may not. In [link], we see an example of a function F

and an initial guess x0

such that the resulting list of numbers approaches a finite value.

Finding a Limit for an Iterative Process

Let F(x)=12x+4

and let x0=0.

For all n≥1,

let xn=F(xn−1).

Find the values x1,x2,x3,x4,x5.

Make a conjecture about what happens to this list of numbers x1,x2,x3…,xn,…

as n→∞.

If the list of numbers x1,x2,x3,…

approaches a finite number x*,

then x*

satisfies x*=F(x*),

and x*

is called a fixed point of F.

If x0=0,

then

x1=12(0)+4=4x2=12(4)+4=6x3=12(6)+4=7x4=12(7)+4=7.5x5=12(7.5)+4=7.75x6=12(7.75)+4=7.875x7=12(7.875)+4=7.9375x8=12(7.9375)+4=7.96875x9=12(7.96875)+4=7.984375.

From this list, we conjecture that the values xn

approach 8.

[link] provides a graphical argument that the values approach 8

as n→∞.

Starting at the point (x0,x0),

we draw a vertical line to the point (x0,F(x0)).

The next number in our list is x1=F(x0).

We use x1

to calculate x2.

Therefore, we draw a horizontal line connecting (x0,x1)

to the point (x1,x1)

on the line y=x,

and then draw a vertical line connecting (x1,x1)

to the point (x1,F(x1)).

The output F(x1)

becomes x2.

Continuing in this way, we could create an infinite number of line segments. These line segments are trapped between the lines F(x)=x2+4

and y=x.

The line segments get closer to the intersection point of these two lines, which occurs when x=F(x).

Solving the equation x=x2+4,

we conclude they intersect at x=8.

Therefore, our graphical evidence agrees with our numerical evidence that the list of numbers x0,x1,x2,…

approaches x*=8

as n→∞.

The function F(x) = (1/2)x + 4 is graphed along with y = x. From x0, which appears to be at the origin, a line is drawn to the function F(x) at x1 = F(x0). Then a line is drawn to the right from here to the line y = x, at which point a line is drawn up to x2 = F(x1). Then a line is drawn to the right from here to the line y = x, at which point a line is drawn up to x3 = F(x2). Continuing this process would converge on the two lines’ intersection point at x* = 8.

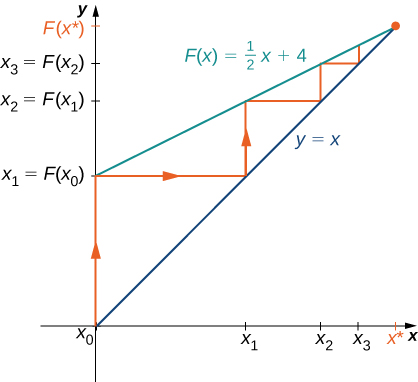
Consider the function F(x)=13x+6.

Let x0=0

and let xn=F(xn−1)

for n≥2.

Find x1,x2,x3,x4,x5.

Make a conjecture about what happens to the list of numbers x1,x2,x3,…xn,…

as n→∞.

x1=6,x2=8,x3=263,x4=809,x5=24227;x*=9
Hint

Consider the point where the lines y=x

and y=F(x)

intersect.

Iterative Processes and Chaos

Iterative processes can yield some very interesting behavior. In this section, we have seen several examples of iterative processes that converge to a fixed point. We also saw in [link] that the iterative process bounced back and forth between two values. We call this kind of behavior a 2

-cycle. Iterative processes can converge to cycles with various periodicities, such as 2−cycles,4−cycles

(where the iterative process repeats a sequence of four values), 8-cycles, and so on.

Some iterative processes yield what mathematicians call chaos. In this case, the iterative process jumps from value to value in a seemingly random fashion and never converges or settles into a cycle. Although a complete exploration of chaos is beyond the scope of this text, in this project we look at one of the key properties of a chaotic iterative process: sensitive dependence on initial conditions. This property refers to the concept that small changes in initial conditions can generate drastically different behavior in the iterative process.

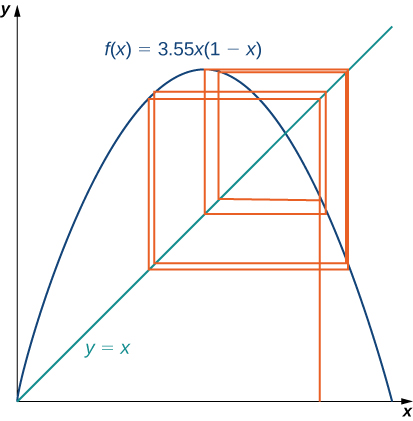
Probably the best-known example of chaos is the Mandelbrot set (see [link]), named after Benoit Mandelbrot (1924–2010), who investigated its properties and helped popularize the field of chaos theory. The Mandelbrot set is usually generated by computer and shows fascinating details on enlargement, including self-replication of the set. Several colorized versions of the set have been shown in museums and can be found online and in popular books on the subject.

A very complicated and organic looking fractal.

In this project we use the logistic map

f(x)=rx(1−x),wherex∈[0,1]andr>0

as the function in our iterative process. The logistic map is a deceptively simple function; but, depending on the value of r,

the resulting iterative process displays some very interesting behavior. It can lead to fixed points, cycles, and even chaos.

To visualize the long-term behavior of the iterative process associated with the logistic map, we will use a tool called a cobweb diagram. As we did with the iterative process we examined earlier in this section, we first draw a vertical line from the point (x0,0)

to the point (x0,f(x0))=(x0,x1).

We then draw a horizontal line from that point to the point (x1,x1),

then draw a vertical line to (x1,f(x1))=(x1,x2),

and continue the process until the long-term behavior of the system becomes apparent. [link] shows the long-term behavior of the logistic map when r=3.55

and x0=0.2.

(The first 100

iterations are not plotted.) The long-term behavior of this iterative process is an 8

-cycle.

In the first quadrant, f(x) = 3.55x(1 – x) is graphed as is y = x. From some point on the x axis, a line is drawn up to the line y = x, at which point it turns to be horizontal and continues until it touches the outside edge of f(x), at which point it turns again to be vertical until it each the line y = x. This process continues a number of times and creates an interesting series of boxes.

  1. Let r=0.5

    and choose

    x0=0.2.

    Either by hand or by using a computer, calculate the first

    10

    values in the sequence. Does the sequence appear to converge? If so, to what value? Does it result in a cycle? If so, what kind of cycle (for example,

    2−cycle,4−cycle.)?
  2. What happens when r=2?
  3. For r=3.2

    and

    r=3.5,

    calculate the first

    100

    sequence values. Generate a cobweb diagram for each iterative process. (Several free applets are available online that generate cobweb diagrams for the logistic map.) What is the long-term behavior in each of these cases?

  4. Now let r=4.

    Calculate the first

    100

    sequence values and generate a cobweb diagram. What is the long-term behavior in this case?

  5. Repeat the process for r=4,

    but let

    x0=0.201.

    How does this behavior compare with the behavior for

    x0=0.2?

Key Concepts

For the following exercises, write Newton’s formula as xn+1=F(xn)

for solving f(x)=0.

f(x)=x2+1
f(x)=x3+2x+1
F(xn)=xn−xn3+2xn+13xn2+2
f(x)=sinx
f(x)=ex
F(xn)=xn−exnexn
f(x)=x3+3xex

For the following exercises, solve f(x)=0

using the iteration xn+1=xn−cf(xn),

which differs slightly from Newton’s method. Find a c

that works and a c

that fails to converge, with the exception of c=0.

f(x)=x2−4,

with x0=0

\|c\|>0.5

fails, \|c\|≤0.5

works

f(x)=x2−4x+3,

with x0=2

What is the value of “c”

for Newton’s method?

c=1f′(xn)

For the following exercises, start at

a. x0=0.6

and

b. x0=2.

Compute x1

and x2

using the specified iterative method.

xn+1=xn2−12
xn+1=2xn(1−xn)

a. x1=1225,x2=312625;

b. x1=−4,x2=−40

xn+1=xn
xn+1=1xn

a. x1=1.291,x2=0.8801;

b. x1=0.7071,x2=1.189

xn+1=3xn(1−xn)
xn+1=xn2+xn−2

a. x1=−2625,x2=−1224625;

b. x1=4,x2=18

xn+1=12xn−1
xn+1=\|xn\|

a. x1=610,x2=610;

b. x1=2,x2=2

For the following exercises, solve to four decimal places using Newton’s method and a computer or calculator. Choose any initial guess x0

that is not the exact root.

x2−10=0
x4−100=0
3.1623or−3.1623
x2−x=0
x3−x=0
0,−1or1
x+5cos(x)=0
x+tan(x)=0,

choose x0∈(−π2,π2)

0
11−x=2
1+x+x2+x3+x4=2
0.5188or−1.2906
x3+(x+1)3=103
x=sin2(x)
0

For the following exercises, use Newton’s method to find the fixed points of the function where f(x)=x;

round to three decimals.

sinx
tan(x)

on x=(π2,3π2)

4.493
ex−2
ln(x)+2
0.159,3.146

Newton’s method can be used to find maxima and minima of functions in addition to the roots. In this case apply Newton’s method to the derivative function f′(x)

to find its roots, instead of the original function. For the following exercises, consider the formulation of the method.

To find candidates for maxima and minima, we need to find the critical points f′(x)=0.

Show that to solve for the critical points of a function f(x),

Newton’s method is given by xn+1=xn−f′(xn)f″(xn).

What additional restrictions are necessary on the function f?

We need f

to be twice continuously differentiable.

For the following exercises, use Newton’s method to find the location of the local minima and/or maxima of the following functions; round to three decimals.

Minimum of f(x)=x2+2x+4

Minimum of f(x)=3x3+2x2−16

x=0

Minimum of f(x)=x2ex

Maximum of f(x)=x+1x

x=−1

Maximum of f(x)=x3+10x2+15x−2

Maximum of f(x)=x−x3x

x=5.619

Minimum of f(x)=x2sinx,

closest non-zero minimum to x=0

Minimum of f(x)=x4+x3+3x2+12x+6

x=−1.326

For the following exercises, use the specified method to solve the equation. If it does not work, explain why it does not work.

Newton’s method, x2+2=0

Newton’s method, 0=ex

There is no solution to the equation.

Newton’s method, 0=1+x2

starting at x0=0

Solving xn+1=−xn3

starting at x0=−1

It enters a cycle.

For the following exercises, use the secant method, an alternative iterative method to Newton’s method. The formula is given by

xn=xn−1−f(xn−1)xn−1−xn−2f(xn−1)−f(xn−2).

Find a root to 0=x2−x−3

accurate to three decimal places.

Find a root to 0=sinx+3x

accurate to four decimal places.

0

Find a root to 0=ex−2

accurate to four decimal places.

Find a root to ln(x+2)=12

accurate to four decimal places.

−0.3513

Why would you use the secant method over Newton’s method? What are the necessary restrictions on f?

For the following exercises, use both Newton’s method and the secant method to calculate a root for the following equations. Use a calculator or computer to calculate how many iterations of each are needed to reach within three decimal places of the exact answer. For the secant method, use the first guess from Newton’s method.

f(x)=x2+2x+1,x0=1

Newton: 11

iterations, secant: 16

iterations

f(x)=x2,x0=1
f(x)=sinx,x0=1

Newton: three iterations, secant: six iterations

f(x)=ex−1,x0=2
f(x)=x3+2x+4,x0=0

Newton: five iterations, secant: eight iterations

In the following exercises, consider Kepler’s equation regarding planetary orbits, M=E−εsin(E),

where M

is the mean anomaly, E

is eccentric anomaly, and ε

measures eccentricity.

Use Newton’s method to solve for the eccentric anomaly E

when the mean anomaly M=π3

and the eccentricity of the orbit ε=0.25;

round to three decimals.

Use Newton’s method to solve for the eccentric anomaly E

when the mean anomaly M=3π2

and the eccentricity of the orbit ε=0.8;

round to three decimals.

E=4.071

The following two exercises consider a bank investment. The initial investment is $10,000.

After 25

years, the investment has tripled to $30,000.

Use Newton’s method to determine the interest rate if the interest was compounded annually.

Use Newton’s method to determine the interest rate if the interest was compounded continuously.

4.394%

The cost for printing a book can be given by the equation C(x)=1000+12x+(12)x2/3.

Use Newton’s method to find the break-even point if the printer sells each book for $20.

Glossary

iterative process
process in which a list of numbers x0,x1,x2,x3…

is generated by starting with a number

x0

and defining

xn=F(xn−1)

for

n≥1
Newton’s method
method for approximating roots of f(x)=0;

using an initial guess

x0;

each subsequent approximation is defined by the equation

xn=xn−1−f(xn−1)f′(xn−1)
Creative Commons License
This work is licensed under a Creative Commons Attribution 4.0 International License.

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1

Attribution: