Maxima and Minima

Given a particular function, we are often interested in determining the largest and smallest values of the function. This information is important in creating accurate graphs. Finding the maximum and minimum values of a function also has practical significance because we can use this method to solve optimization problems, such as maximizing profit, minimizing the amount of material used in manufacturing an aluminum can, or finding the maximum height a rocket can reach. In this section, we look at how to use derivatives to find the largest and smallest values for a function.

Absolute Extrema

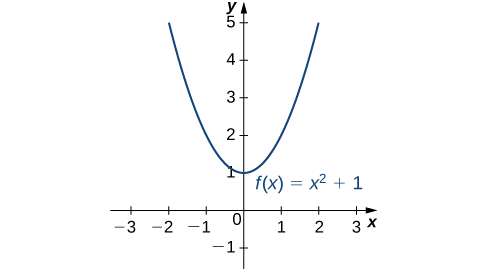
Consider the function f(x)=x2+1

over the interval (−∞,∞).

As x→±∞,

f(x)→∞.

Therefore, the function does not have a largest value. However, since x2+1≥1

for all real numbers x

and x2+1=1

when x=0,

the function has a smallest value, 1, when x=0.

We say that 1 is the absolute minimum of f(x)=x2+1

and it occurs at x=0.

We say that f(x)=x2+1

does not have an absolute maximum (see the following figure).

The function f(x) = x2 + 1 is graphed, and its minimum of 1 is seen to be at x = 0.

Definition

Let f

be a function defined over an interval I

and let c∈I.

We say f

has an absolute maximum on I

at c

if f(c)≥f(x)

for all x∈I.

We say f

has an absolute minimum on I

at c

if f(c)≤f(x)

for all x∈I.

If f

has an absolute maximum on I

at c

or an absolute minimum on I

at c,

we say f

has an absolute extremum on I

at c.

Before proceeding, let’s note two important issues regarding this definition. First, the term absolute here does not refer to absolute value. An absolute extremum may be positive, negative, or zero. Second, if a function f

has an absolute extremum over an interval I

at c,

the absolute extremum is f(c).

The real number c

is a point in the domain at which the absolute extremum occurs. For example, consider the function f(x)=1/(x2+1)

over the interval (−∞,∞).

Since

f(0)=1≥1x2+1=f(x)

for all real numbers x,

we say f

has an absolute maximum over (−∞,∞)

at x=0.

The absolute maximum is f(0)=1.

It occurs at x=0,

as shown in [link](b).

A function may have both an absolute maximum and an absolute minimum, just one extremum, or neither. [link] shows several functions and some of the different possibilities regarding absolute extrema. However, the following theorem, called the Extreme Value Theorem, guarantees that a continuous function f

over a closed, bounded interval [a,b]

has both an absolute maximum and an absolute minimum.

This figure has six parts a, b, c, d, e, and f. In figure a, the line f(x) = x3 is shown, and it is noted that it has no absolute minimum and no absolute maximum. In figure b, the line f(x) = 1/(x2 + 1) is shown, which is near 0 for most of its length and rises to a bump at (0, 1); it has no absolute minimum, but does have an absolute maximum of 1 at x = 0. In figure c, the line f(x) = cos x is shown, which has absolute minimums of −1 at ±π, ±3π, … and absolute maximums of 1 at 0, ±2π, ±4π, …. In figure d, the piecewise function f(x) = 2 – x2 for 0 ≤ x < 2 and x – 3 for 2 ≤ x ≤ 4 is shown, with absolute maximum of 2 at x = 0 and no absolute minimum. In figure e, the function f(x) = (x – 2)2 is shown on [1, 4], which has absolute maximum of 4 at x = 4 and absolute minimum of 0 at x = 2. In figure f, the function f(x) = x/(2 − x) is shown on [0, 2), with absolute minimum of 0 at x = 0 and no absolute maximum.

Extreme Value Theorem

If f

is a continuous function over the closed, bounded interval [a,b],

then there is a point in [a,b]

at which f

has an absolute maximum over [a,b]

and there is a point in [a,b]

at which f

has an absolute minimum over [a,b].

The proof of the extreme value theorem is beyond the scope of this text. Typically, it is proved in a course on real analysis. There are a couple of key points to note about the statement of this theorem. For the extreme value theorem to apply, the function must be continuous over a closed, bounded interval. If the interval I

is open or the function has even one point of discontinuity, the function may not have an absolute maximum or absolute minimum over I.

For example, consider the functions shown in [link](d), (e), and (f). All three of these functions are defined over bounded intervals. However, the function in graph (e) is the only one that has both an absolute maximum and an absolute minimum over its domain. The extreme value theorem cannot be applied to the functions in graphs (d) and (f) because neither of these functions is continuous over a closed, bounded interval. Although the function in graph (d) is defined over the closed interval [0,4],

the function is discontinuous at x=2.

The function has an absolute maximum over [0,4]

but does not have an absolute minimum. The function in graph (f) is continuous over the half-open interval [0,2),

but is not defined at x=2,

and therefore is not continuous over a closed, bounded interval. The function has an absolute minimum over [0,2),

but does not have an absolute maximum over [0,2).

These two graphs illustrate why a function over a bounded interval may fail to have an absolute maximum and/or absolute minimum.

Before looking at how to find absolute extrema, let’s examine the related concept of local extrema. This idea is useful in determining where absolute extrema occur.

Local Extrema and Critical Points

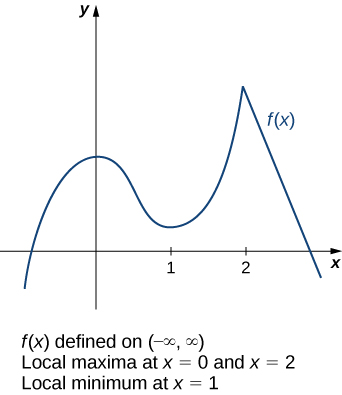
Consider the function f

shown in [link]. The graph can be described as two mountains with a valley in the middle. The absolute maximum value of the function occurs at the higher peak, at x=2.

However, x=0

is also a point of interest. Although f(0)

is not the largest value of f,

the value f(0)

is larger than f(x)

for all x

near 0. We say f

has a local maximum at x=0.

Similarly, the function f

does not have an absolute minimum, but it does have a local minimum at x=1

because f(1)

is less than f(x)

for x

near 1.

The function f(x) is shown, which curves upward from quadrant III, slows down in quadrant II, achieves a local maximum on the y-axis, decreases to achieve a local minimum in quadrant I at x = 1, increases to a local maximum at x = 2 that is greater than the other local maximum, and then decreases rapidly through quadrant IV.

Definition

A function f

has a local maximum at c

if there exists an open interval I

containing c

such that I

is contained in the domain of f

and f(c)≥f(x)

for all x∈I.

A function f

has a local minimum at c

if there exists an open interval I

containing c

such that I

is contained in the domain of f

and f(c)≤f(x)

for all x∈I.

A function f

has a local extremum at c

if f

has a local maximum at c

or f

has a local minimum at c.

Note that if f

has an absolute extremum at c

and f

is defined over an interval containing c,

then f(c)

is also considered a local extremum. If an absolute extremum for a function f

occurs at an endpoint, we do not consider that to be a local extremum, but instead refer to that as an endpoint extremum.

Given the graph of a function f,

it is sometimes easy to see where a local maximum or local minimum occurs. However, it is not always easy to see, since the interesting features on the graph of a function may not be visible because they occur at a very small scale. Also, we may not have a graph of the function. In these cases, how can we use a formula for a function to determine where these extrema occur?

To answer this question, let’s look at [link] again. The local extrema occur at x=0,

x=1,

and x=2.

Notice that at x=0

and x=1,

the derivative f′(x)=0.

At x=2,

the derivative f′(x)

does not exist, since the function f

has a corner there. In fact, if f

has a local extremum at a point x=c,

the derivative f′(c)

must satisfy one of the following conditions: either f′(c)=0

or f′(c)

is undefined. Such a value c

is known as a critical point and it is important in finding extreme values for functions.

Definition

Let c

be an interior point in the domain of f.

We say that c

is a critical point of f

if f′(c)=0

or f′(c)

is undefined.

As mentioned earlier, if f

has a local extremum at a point x=c,

then c

must be a critical point of f.

This fact is known as Fermat’s theorem.

Fermat’s Theorem

If f

has a local extremum at c

and f

is differentiable at c,

then f′(c)=0.

Proof

Suppose f

has a local extremum at c

and f

is differentiable at c.

We need to show that f′(c)=0.

To do this, we will show that f′(c)≥0

and f′(c)≤0,

and therefore f′(c)=0.

Since f

has a local extremum at c,

f

has a local maximum or local minimum at c.

Suppose f

has a local maximum at c.

The case in which f

has a local minimum at c

can be handled similarly. There then exists an open interval I

such that f(c)≥f(x)

for all x∈I.

Since f

is differentiable at c,

from the definition of the derivative, we know that

f′(c)=limx→cf(x)−f(c)x−c.

Since this limit exists, both one-sided limits also exist and equal f′(c).

Therefore,

f′(c)=limx→c+f(x)−f(c)x−c,

and

f′(c)=limx→c−f(x)−f(c)x−c.

Since f(c)

is a local maximum, we see that f(x)−f(c)≤0

for x

near c.

Therefore, for x

near c,

but x>c,

we have f(x)−f(c)x−c≤0.

From [link] we conclude that f′(c)≤0.

Similarly, it can be shown that f′(c)≥0.

Therefore, f′(c)=0.

□

From Fermat’s theorem, we conclude that if f

has a local extremum at c,

then either f′(c)=0

or f′(c)

is undefined. In other words, local extrema can only occur at critical points.

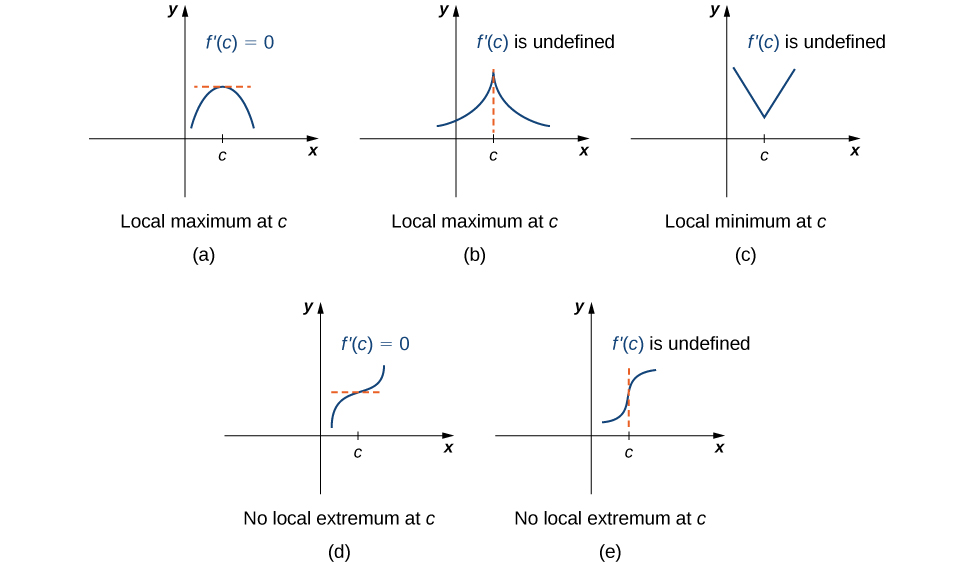
Note this theorem does not claim that a function f

must have a local extremum at a critical point. Rather, it states that critical points are candidates for local extrema. For example, consider the function f(x)=x3.

We have f′(x)=3x2=0

when x=0.

Therefore, x=0

is a critical point. However, f(x)=x3

is increasing over (−∞,∞),

and thus f

does not have a local extremum at x=0.

In [link], we see several different possibilities for critical points. In some of these cases, the functions have local extrema at critical points, whereas in other cases the functions do not. Note that these graphs do not show all possibilities for the behavior of a function at a critical point.

This figure has five parts a, b, c, d, and e. In figure a, a parabola is shown facing down in quadrant I; there is a horizontal tangent line at the local maximum marked f’(c) = 0. In figure b, there is a function drawn with an asymptote at c, meaning that the function increases toward infinity on both sides of c; it is noted that f’(c) is undefined. In figure c, a version of the absolute value graph is shown that has been shifted so that its minimum is in quadrant I with x = c. It is noted that f’(c) is undefined. In figure d, a version of the function f(x) = x3 is shown that has been shifted so that its inflection point is in quadrant I with x = c. Its inflection point at (c, f(c)) has a horizontal line through it, and it is noted that f’(c) = 0. In figure e, a version of the function f(x) = x1/3 is shown that has been shifted so that its inflection point is in quadrant I with x = c. Its inflection point at (c, f(c)) has a vertical line through it, and it is noted that f’(c) is undefined.

Later in this chapter we look at analytical methods for determining whether a function actually has a local extremum at a critical point. For now, let’s turn our attention to finding critical points. We will use graphical observations to determine whether a critical point is associated with a local extremum.

Locating Critical Points

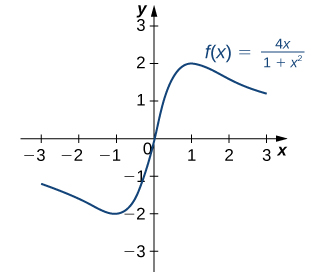
For each of the following functions, find all critical points. Use a graphing utility to determine whether the function has a local extremum at each of the critical points.

  1. f(x)=13x3−52x2+4x
  2. f(x)=(x2−1)3
  3. f(x)=4x1+x2
  1. The derivative f′(x)=x2−5x+4

    is defined for all real numbers

    x.

    Therefore, we only need to find the values for

    x

    where

    f′(x)=0.

    Since

    f′(x)=x2−5x+4=(x−4)(x−1),

    the critical points are

    x=1

    and

    x=4.

    From the graph of

    f

    in [link], we see that

    f

    has a local maximum at

    x=1

    and a local minimum at

    x=4.

    The function f(x) = (1/3) x3 – (5/2) x2 + 4x is graphed. The function has local maximum at x = 1 and local minimum at x = 4.

  2. Using the chain rule, we see the derivative is
    f′(x)=3(x2−1)2(2x)=6x(x2−1)2.

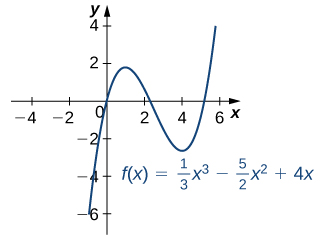
    Therefore,

    f

    has critical points when

    x=0

    and when

    x2−1=0.

    We conclude that the critical points are

    x=0,±1.

    From the graph of

    f

    in [link], we see that

    f

    has a local (and absolute) minimum at

    x=0,

    but does not have a local extremum at

    x=1

    or

    x=−1.

    The function f(x) = (x2 − 1)3 is graphed. The function has local minimum at x = 0, and inflection points at x = ±1.

  3. By the chain rule, we see that the derivative is
    f′(x)=(1+x24)−4x(2x)(1+x2)2=4−4x2(1+x2)2.

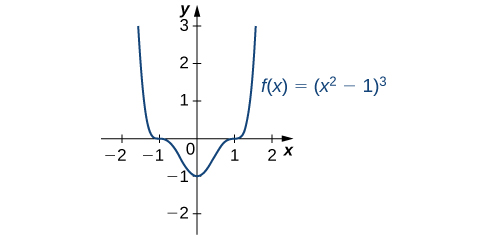
    The derivative is defined everywhere. Therefore, we only need to find values for

    x

    where

    f′(x)=0.

    Solving

    f′(x)=0,

    we see that

    4−4x2=0,

    which implies

    x=±1.

    Therefore, the critical points are

    x=±1.

    From the graph of

    f

    in [link], we see that

    f

    has an absolute maximum at

    x=1

    and an absolute minimum at

    x=−1.

    Hence,

    f

    has a local maximum at

    x=1

    and a local minimum at

    x=−1.

    (Note that if

    f

    has an absolute extremum over an interval

    I

    at a point

    c

    that is not an endpoint of

    I,

    then

    f

    has a local extremum at

    c.)

    The function f(x) = 4x/(1 + x2) is graphed. The function has local/absolute maximum at x = 1 and local/absolute minimum at x = −1.

Find all critical points for f(x)=x3−12x2−2x+1.

x=−23, x=1
Hint

Calculate f′(x).

Locating Absolute Extrema

The extreme value theorem states that a continuous function over a closed, bounded interval has an absolute maximum and an absolute minimum. As shown in [link], one or both of these absolute extrema could occur at an endpoint. If an absolute extremum does not occur at an endpoint, however, it must occur at an interior point, in which case the absolute extremum is a local extremum. Therefore, by [link], the point c

at which the local extremum occurs must be a critical point. We summarize this result in the following theorem.

Location of Absolute Extrema

Let f

be a continuous function over a closed, bounded interval I.

The absolute maximum of f

over I

and the absolute minimum of f

over I

must occur at endpoints of I

or at critical points of f

in I.

With this idea in mind, let’s examine a procedure for locating absolute extrema.

Problem-Solving Strategy: Locating Absolute Extrema over a Closed Interval

Consider a continuous function f

defined over the closed interval [a,b].

  1. Evaluate f

    at the endpoints

    x=a

    and

    x=b.
  2. Find all critical points of f

    that lie over the interval

    (a,b)

    and evaluate

    f

    at those critical points.

  3. Compare all values found in (1) and (2). From [link], the absolute extrema must occur at endpoints or critical points. Therefore, the largest of these values is the absolute maximum of f.

    The smallest of these values is the absolute minimum of

    f.

Now let’s look at how to use this strategy to find the absolute maximum and absolute minimum values for continuous functions.

Locating Absolute Extrema

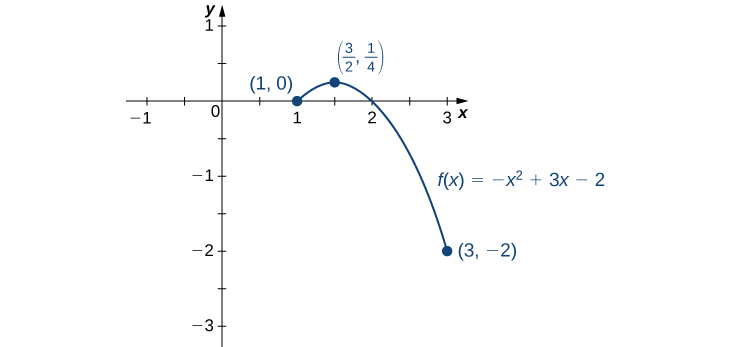
For each of the following functions, find the absolute maximum and absolute minimum over the specified interval and state where those values occur.

  1. f(x)=−x2+3x−2

    over

    [1,3].
  2. f(x)=x2−3x2/3

    over

    [0,2].
  1. Step 1. Evaluate f

    at the endpoints

    x=1

    and

    x=3.
    f(1)=0andf(3)=−2

    Step 2. Since

    f′(x)=−2x+3, f′

    is defined for all real numbers

    x.

    Therefore, there are no critical points where the derivative is undefined. It remains to check where

    f′(x)=0.

    Since

    f′(x)=−2x+3=0

    at

    x=32

    and

    32

    is in the interval

    [1,3], f(32)

    is a candidate for an absolute extremum of

    f

    over

    [1,3].

    We evaluate

    f(32)

    and find

    f(32)=14.

    Step 3. We set up the following table to compare the values found in steps 1 and 2.

    x
    f(x)
    Conclusion  
    {: valign=”top”} ———-
    0  
    0
     
    32
    14
    Absolute maximum
    3
    −2
    Absolute minimum

    From the table, we find that the absolute maximum of

    f

    over the interval [1, 3] is

    14,

    and it occurs at

    x=32.

    The absolute minimum of

    f

    over the interval [1, 3] is

    −2,

    and it occurs at

    x=3

    as shown in the following graph.

    The function f(x) = – x2 + 3x – 2 is graphed from (1, 0) to (3, −2), with its maximum marked at (3/2, 1/4).

  2. Step 1. Evaluate f

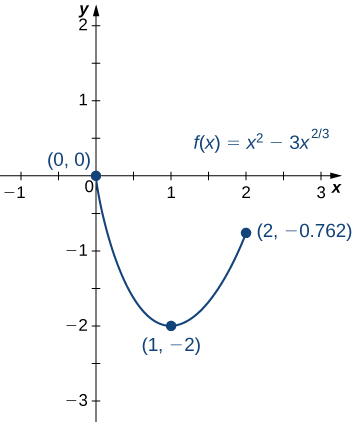
    at the endpoints

    x=0

    and

    x=2.
    f(0)=0andf(2)=4−343≈−0.762

    Step 2. The derivative of

    f

    is given by

    f′(x)=2x−2x1/3=2x4/3−2x1/3

    for

    x≠0.

    The derivative is zero when

    2x4/3−2=0,

    which implies

    x=±1.

    The derivative is undefined at

    x=0.

    Therefore, the critical points of

    f

    are

    x=0,1,−1.

    The point

    x=0

    is an endpoint, so we already evaluated

    f(0)

    in step 1. The point

    x=−1

    is not in the interval of interest, so we need only evaluate

    f(1).

    We find that

    f(1)=−2.

    Step 3. We compare the values found in steps 1 and 2, in the following table.

    x
    f(x)
    Conclusion  
    {: valign=”top”} ———-
    0  
    0
    Absolute maximum
    1
    −2
    Absolute minimum
    2
    −0.762
     

    We conclude that the absolute maximum of

    f

    over the interval [0, 2] is zero, and it occurs at

    x=0.

    The absolute minimum is −2, and it occurs at

    x=1

    as shown in the following graph.

    The function f(x) = x2 – 3x2/3 is graphed from (0, 0) to (2, −0.762), with its minimum marked at (1, −2).

Find the absolute maximum and absolute minimum of f(x)=x2−4x+3

over the interval [1,4].

The absolute maximum is 3

and it occurs at x=4.

The absolute minimum is −1

and it occurs at x=2.

Hint

Look for critical points. Evaluate f

at all critical points and at the endpoints.

At this point, we know how to locate absolute extrema for continuous functions over closed intervals. We have also defined local extrema and determined that if a function f

has a local extremum at a point c,

then c

must be a critical point of f.

However, c

being a critical point is not a sufficient condition for f

to have a local extremum at c.

Later in this chapter, we show how to determine whether a function actually has a local extremum at a critical point. First, however, we need to introduce the Mean Value Theorem, which will help as we analyze the behavior of the graph of a function.

Key Concepts

In precalculus, you learned a formula for the position of the maximum or minimum of a quadratic equation y=ax2+bx+c,

which was m=−b(2a).

Prove this formula using calculus.

If you are finding an absolute minimum over an interval [a,b],

why do you need to check the endpoints? Draw a graph that supports your hypothesis.

Answers may vary

If you are examining a function over an interval (a,b),

for a

and b

finite, is it possible not to have an absolute maximum or absolute minimum?

When you are checking for critical points, explain why you also need to determine points where f(x)

is undefined. Draw a graph to support your explanation.

Answers will vary

Can you have a finite absolute maximum for y=ax2+bx+c

over (−∞,∞)?

Explain why or why not using graphical arguments.

Can you have a finite absolute maximum for y=ax3+bx2+cx+d

over (−∞,∞)

assuming a is non-zero? Explain why or why not using graphical arguments.

No; answers will vary

Let m

be the number of local minima and M

be the number of local maxima. Can you create a function where M>m+2?

Draw a graph to support your explanation.

Is it possible to have more than one absolute maximum? Use a graphical argument to prove your hypothesis.

Since the absolute maximum is the function (output) value rather than the x value, the answer is no; answers will vary

Is it possible to have no absolute minimum or maximum for a function? If so, construct such a function. If not, explain why this is not possible.

[T] Graph the function y=eax.

For which values of a,

on any infinite domain, will you have an absolute minimum and absolute maximum?

When a=0

For the following exercises, determine where the local and absolute maxima and minima occur on the graph given. Assume domains are closed intervals unless otherwise specified.

![The function graphed starts at (−4, 60), decreases rapidly to (−3, −40), increases to (−1, 10) before decreasing slowly to (2, 0), at which point it increases rapidly to (3, 30).](/calculus-book/resources/CNX_Calc_Figure_04_03_201.jpg)
![The function graphed starts at (−2.2, 10), decreases rapidly to (−2, −11), increases to (−1, 5) before decreasing slowly to (1, 3), at which point it increases to (2, 7), and then decreases to (3, −20).](/calculus-book/resources/CNX_Calc_Figure_04_03_202.jpg)

Absolute minimum at 3; Absolute maximum at −2.2; local minima at −2, 1; local maxima at −1, 2

![The function graphed starts at (−3, −1), increases rapidly to (−2, 0.7), decreases to (−1, −0.25) before decreasing slowly to (1, 0.25), at which point it decreases to (2, 0.7), and then increases to (3, 1).](/calculus-book/resources/CNX_Calc_Figure_04_03_203.jpg)
![The function graphed starts at (−2.5, 1), decreases rapidly to (−2, −1.25), increases to (−1, 0.25) before decreasing slowly to (0, 0.2), at which point it increases slowly to (1, 0.25), then decreases rapidly to (2, −1.25), and finally increases to (2.5, 1).](/calculus-book/resources/CNX_Calc_Figure_04_03_204.jpg)

Absolute minima at −2, 2; absolute maxima at −2.5, 2.5; local minimum at 0; local maxima at −1, 1

For the following problems, draw graphs of f(x),

which is continuous, over the interval [−4,4]

with the following properties:

Absolute maximum at x=2

and absolute minima at x=±3

Absolute minimum at x=1

and absolute maximum at x=2

Answers may vary.

Absolute maximum at x=4,

absolute minimum at x=−1,

local maximum at x=−2,

and a critical point that is not a maximum or minimum at x=2

Absolute maxima at x=2

and x=−3,

local minimum at x=1,

and absolute minimum at x=4

Answers may vary.

For the following exercises, find the critical points in the domains of the following functions.

y=4x3−3x
y=4x−x2
x=1
y=1x−1
y=ln(x−2)

None

y=tan(x)
y=4−x2
x=0
y=x3/2−3x5/2
y=x2−1x2+2x−3

None

y=sin2(x)
y=x+1x
x=−1,1

For the following exercises, find the local and/or absolute maxima for the functions over the specified domain.

f(x)=x2+3

over [−1,4]

y=x2+2x

over [1,4]

Absolute maximum: x=4,

y=332;

absolute minimum: x=1,

y=3
y=(x−x2)2

over [−1,1]

y=1(x−x2)

over [0,1]

Absolute minimum: x=12,

y=4
y=9−x

over [1,9]

y=x+sin(x)

over [0,2π]

Absolute maximum: x=2π,

y=2π;

absolute minimum: x=0,

y=0
y=x1+x

over [0,100]

y=\|x+1\|+\|x−1\|

over [−3,2]

Absolute maximum: x=−3;

absolute minimum: −1≤x≤1,

y=2
y=x−x3

over [0,4]

y=sinx+cosx

over [0,2π]

Absolute maximum: x=π4,

y=2;

absolute minimum: x=5π4,

y=−2
y=4sinθ−3cosθ

over [0,2π]

For the following exercises, find the local and absolute minima and maxima for the functions over (−∞,∞).

y=x2+4x+5

Absolute minimum: x=−2,

y=1
y=x3−12x
y=3x4+8x3−18x2

Absolute minimum: x=−3,

y=−135;

local maximum: x=0,

y=0;

local minimum: x=1,

y=−7
y=x3(1−x)6
y=x2+x+6x−1

Local maximum: x=1−22,

y=3−42;

local minimum: x=1+22,

y=3+42
y=x2−1x−1

For the following functions, use a calculator to graph the function and to estimate the absolute and local maxima and minima. Then, solve for them explicitly.

[T] y=3x1−x2

Absolute maximum: x=22,

y=32;

absolute minimum: x=−22,

y=−32

[T] y=x+sin(x)

[T] y=12x5+45x4+20x3−90x2−120x+3

Local maximum: x=−2,

y=59;

local minimum: x=1,

y=−130

[T] y=x3+6x2−x−30x−2

[T] y=4−x24+x2

Absolute maximum: x=0,

y=1;

absolute minimum: x=−2,2,

y=0

A company that produces cell phones has a cost function of C=x2−1200x+36,400,

where C

is cost in dollars and x

is number of cell phones produced (in thousands). How many units of cell phone (in thousands) minimizes this cost function?

A ball is thrown into the air and its position is given by h(t)=−4.9t2+60t+5m.

Find the height at which the ball stops ascending. How long after it is thrown does this happen?

h=924549m, t=30049s

For the following exercises, consider the production of gold during the California gold rush (1848–1888). The production of gold can be modeled by G(t)=(25t)(t2+16),

where t

is the number of years since the rush began (0≤t≤40)

and G

is ounces of gold produced (in millions). A summary of the data is shown in the following figure.

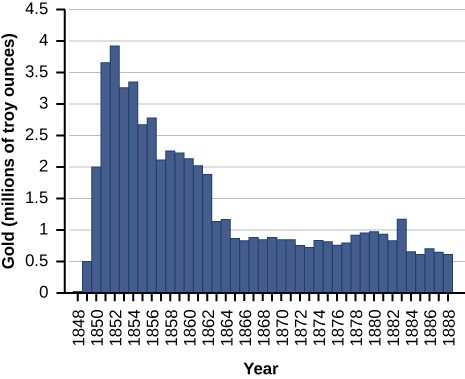
The bar graph shows gold (in millions of troy ounces) per year, starting in 1848 and ending in 1888. In 1848, the bar graph shows 0.05; in 1849, 0.5; in 1850, 2; in 1851, 3.6; in 1852, 3.9; in 1853, 3.3; in 1854, 3.4; in 1855, 2.6; in 1856, 2.75; in 1857, 2.1; in 1858, 2.2; in 1859, 2.15; in 1860, 2.1; in 1861, 2; in 1862, 1.8; in 1863, 1.1; in 1864, 1.15; in 1865, 0.9; in 1866, 0.85; in 1867, 0.9; in 1868, 0.85; in 1869, 0.9; in 1870, 0.85; in 1871, 0.85; in 1872, 0.75; in 1873, 0.7; in 1874, 0.8; in 1875, 0.75; in 1876, 0.7; in 1877, 0.73; in 1878, 0.9; in 1879, 0.95; in 1880, 1; in 1881, 0.95; in 1882, 0.85; in 1883, 1.1; in 1884, 0.6; in 1885, 0.55; in 1886, 0.65; in 1887, 0.6; and in 1888, 0.55.

Find when the maximum (local and global) gold production occurred, and the amount of gold produced during that maximum.

Find when the minimum (local and global) gold production occurred. What was the amount of gold produced during this minimum?

The global minimum was in 1848, when no gold was produced.

Find the critical points, maxima, and minima for the following piecewise functions.

y={x2−4x0≤x≤1x2−41<x≤2
y={x2+1x≤1x2−4x+5x>1

Absolute minima: x=0,

x=2, y=1;

local maximum at x=1,

y=2

For the following exercises, find the critical points of the following generic functions. Are they maxima, minima, or neither? State the necessary conditions.

y=ax2+bx+c,

given that a>0

y=(x−1)a,

given that a>1

No maxima/minima if a

is odd, minimum at x=1

if a

is even

Glossary

absolute extremum
if f

has an absolute maximum or absolute minimum at

c,

we say

f

has an absolute extremum at

c
absolute maximum
if f(c)≥f(x)

for all

x

in the domain of

f,

we say

f

has an absolute maximum at

c
absolute minimum
if f(c)≤f(x)

for all

x

in the domain of

f,

we say

f

has an absolute minimum at

c
critical point
if f′(c)=0

or

f′(c)

is undefined, we say that

c

is a critical point of

f
extreme value theorem
if f

is a continuous function over a finite, closed interval, then

f

has an absolute maximum and an absolute minimum

Fermat’s theorem
if f

has a local extremum at

c,

then

c

is a critical point of

f
local extremum
if f

has a local maximum or local minimum at

c,

we say

f

has a local extremum at

c
local maximum
if there exists an interval I

such that

f(c)≥f(x)

for all

x∈I,

we say

f

has a local maximum at

c
local minimum
if there exists an interval I

such that

f(c)≤f(x)

for all

x∈I,

we say

f

has a local minimum at

c
Creative Commons License
This work is licensed under a Creative Commons Attribution 4.0 International License.

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1

Attribution: