We have just seen how derivatives allow us to compare related quantities that are changing over time. In this section, we examine another application of derivatives: the ability to approximate functions locally by linear functions. Linear functions are the easiest functions with which to work, so they provide a useful tool for approximating function values. In addition, the ideas presented in this section are generalized later in the text when we study how to approximate functions by higher-degree polynomials Introduction to Power Series and Functions.
Consider a function
that is differentiable at a point
Recall that the tangent line to the graph of
at
is given by the equation
For example, consider the function
at
Since
is differentiable at
and
we see that
Therefore, the tangent line to the graph of
at
is given by the equation
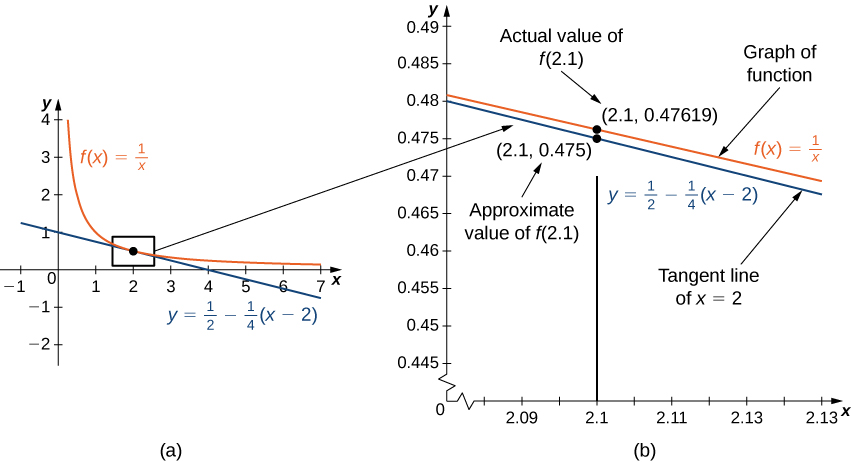
[link](a) shows a graph of
along with the tangent line to
at
Note that for
near 2, the graph of the tangent line is close to the graph of
As a result, we can use the equation of the tangent line to approximate
for
near 2. For example, if
the
value of the corresponding point on the tangent line is
The actual value of
is given by
Therefore, the tangent line gives us a fairly good approximation of
([link](b)). However, note that for values of
far from 2, the equation of the tangent line does not give us a good approximation. For example, if
the
-value of the corresponding point on the tangent line is
whereas the value of the function at
is

In general, for a differentiable function
the equation of the tangent line to
at
can be used to approximate
for
near
Therefore, we can write
We call the linear function
the linear approximation, or tangent line approximation, of
at
This function
is also known as the linearization of
at
To show how useful the linear approximation can be, we look at how to find the linear approximation for
at
Find the linear approximation of
at
and use the approximation to estimate
Since we are looking for the linear approximation at
using [link] we know the linear approximation is given by
We need to find
and
Therefore, the linear approximation is given by [link].
Using the linear approximation, we can estimate
by writing
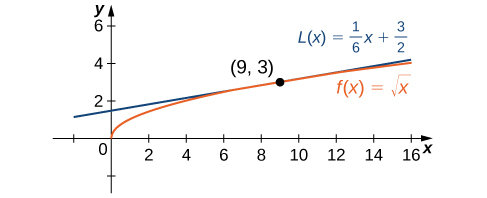
Using a calculator, the value of
to four decimal places is 3.0166. The value given by the linear approximation, 3.0167, is very close to the value obtained with a calculator, so it appears that using this linear approximation is a good way to estimate
at least for
near
At the same time, it may seem odd to use a linear approximation when we can just push a few buttons on a calculator to evaluate
However, how does the calculator evaluate
The calculator uses an approximation! In fact, calculators and computers use approximations all the time to evaluate mathematical expressions; they just use higher-degree approximations.
Find the local linear approximation to
at
Use it to approximate
to five decimal places.
2.00833
Find the linear approximation of
at
and use it to approximate
First we note that since
rad is equivalent to
using the linear approximation at
seems reasonable. The linear approximation is given by
We see that
Therefore, the linear approximation of
at
is given by [link].
To estimate
using
we must first convert
to radians. We have
radians, so the estimate for
is given by
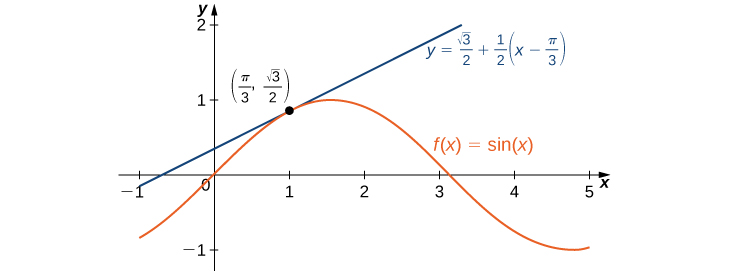
Find the linear approximation for
at
Linear approximations may be used in estimating roots and powers. In the next example, we find the linear approximation for
at
which can be used to estimate roots and powers for real numbers near 1. The same idea can be extended to a function of the form
to estimate roots and powers near a different number
Find the linear approximation of
at
Use this approximation to estimate
The linear approximation at
is given by
Because
the linear approximation is given by [link](a).
We can approximate
by evaluating
when
We conclude that
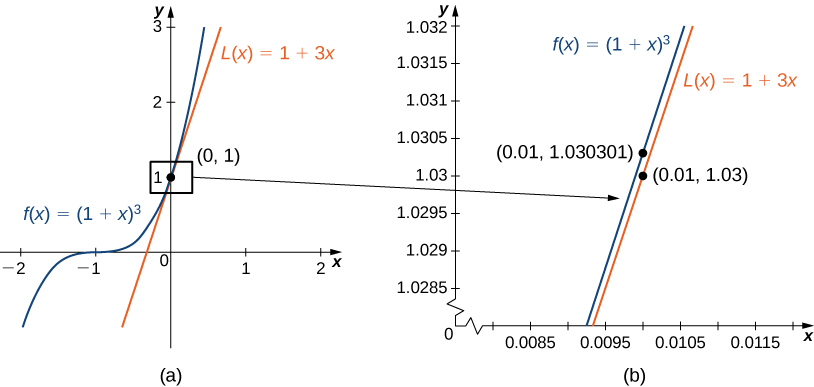
Find the linear approximation of
at
without using the result from the preceding example.
We have seen that linear approximations can be used to estimate function values. They can also be used to estimate the amount a function value changes as a result of a small change in the input. To discuss this more formally, we define a related concept: differentials. Differentials provide us with a way of estimating the amount a function changes as a result of a small change in input values.
When we first looked at derivatives, we used the Leibniz notation
to represent the derivative of
with respect to
Although we used the expressions dy and dx in this notation, they did not have meaning on their own. Here we see a meaning to the expressions dy and dx. Suppose
is a differentiable function. Let dx be an independent variable that can be assigned any nonzero real number, and define the dependent variable
by
It is important to notice that
is a function of both
and
The expressions dy and dx are called differentials. We can divide both sides of [link] by
which yields
This is the familiar expression we have used to denote a derivative. [link] is known as the differential form of [link].
For each of the following functions, find dy and evaluate when
and
The key step is calculating the derivative. When we have that, we can obtain dy directly.
we know
and therefore
When
and
This gives us
When
and
For
find
We now connect differentials to linear approximations. Differentials can be used to estimate the change in the value of a function resulting from a small change in input values. Consider a function
that is differentiable at point
Suppose the input
changes by a small amount. We are interested in how much the output
changes. If
changes from
to
then the change in
is
(also denoted
and the change in
is given by
Instead of calculating the exact change in
however, it is often easier to approximate the change in
by using a linear approximation. For
near
can be approximated by the linear approximation
Therefore, if
is small,
That is,
In other words, the actual change in the function
if
increases from
to
is approximately the difference between
and
where
is the linear approximation of
at
By definition of
this difference is equal to
In summary,
Therefore, we can use the differential
to approximate the change in
if
increases from
to
We can see this in the following graph.
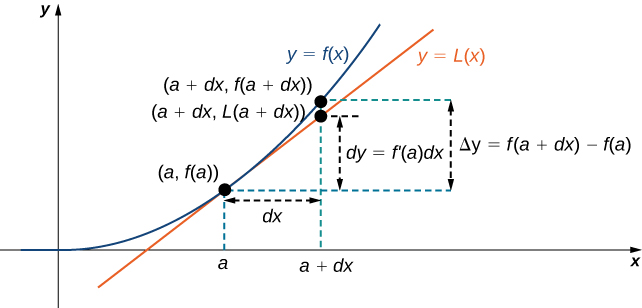
We now take a look at how to use differentials to approximate the change in the value of the function that results from a small change in the value of the input. Note the calculation with differentials is much simpler than calculating actual values of functions and the result is very close to what we would obtain with the more exact calculation.
Let
Compute
and dy at
if
The actual change in
if
changes from
to
is given by
The approximate change in
is given by
Since
we have
For
find
and
at
if
Any type of measurement is prone to a certain amount of error. In many applications, certain quantities are calculated based on measurements. For example, the area of a circle is calculated by measuring the radius of the circle. An error in the measurement of the radius leads to an error in the computed value of the area. Here we examine this type of error and study how differentials can be used to estimate the error.
Consider a function
with an input that is a measured quantity. Suppose the exact value of the measured quantity is
but the measured value is
We say the measurement error is dx (or
As a result, an error occurs in the calculated quantity
This type of error is known as a propagated error and is given by
Since all measurements are prone to some degree of error, we do not know the exact value of a measured quantity, so we cannot calculate the propagated error exactly. However, given an estimate of the accuracy of a measurement, we can use differentials to approximate the propagated error
Specifically, if
is a differentiable function at
the propagated error is
Unfortunately, we do not know the exact value
However, we can use the measured value
and estimate
In the next example, we look at how differentials can be used to estimate the error in calculating the volume of a box if we assume the measurement of the side length is made with a certain amount of accuracy.
Suppose the side length of a cube is measured to be 5 cm with an accuracy of 0.1 cm.
cm. Therefore,
The volume of a cube is given by
which leads to
Using the measured side length of 5 cm, we can estimate that
Therefore,
If the side length is actually 5.1 cm, then the volume of the cube is
Therefore, the actual volume of the cube is between 117.649 and 132.651. Since the side length is measured to be 5 cm, the computed volume is
Therefore, the error in the computed volume is
That is,
We see the estimated error
is relatively close to the actual potential error in the computed volume.
Estimate the error in the computed volume of a cube if the side length is measured to be 6 cm with an accuracy of 0.2 cm.
The volume measurement is accurate to within
The measurement error dx
and the propagated error
are absolute errors. We are typically interested in the size of an error relative to the size of the quantity being measured or calculated. Given an absolute error
for a particular quantity, we define the relative error as
where
is the actual value of the quantity. The percentage error is the relative error expressed as a percentage. For example, if we measure the height of a ladder to be 63 in. when the actual height is 62 in., the absolute error is 1 in. but the relative error is
or
By comparison, if we measure the width of a piece of cardboard to be 8.25 in. when the actual width is 8 in., our absolute error is
in., whereas the relative error is
or
Therefore, the percentage error in the measurement of the cardboard is larger, even though 0.25 in. is less than 1 in.
An astronaut using a camera measures the radius of Earth as 4000 mi with an error of
mi. Let’s use differentials to estimate the relative and percentage error of using this radius measurement to calculate the volume of Earth, assuming the planet is a perfect sphere.
If the measurement of the radius is accurate to within
we have
Since the volume of a sphere is given by
we have
Using the measured radius of 4000 mi, we can estimate
To estimate the relative error, consider
Since we do not know the exact value of the volume
use the measured radius
to estimate
We obtain
Therefore the relative error satisfies
which simplifies to
The relative error is 0.06 and the percentage error is
Determine the percentage error if the radius of Earth is measured to be 3950 mi with an error of
mi.
7.6%
Use the fact that
to find
can be approximated at
by the linear function
if
changes from
to
then
is an approximation for the change in
The actual change in
is
can lead to an error in a calculated quantity
The error in the calculated quantity is known as the propagated error. The propagated error can be estimated by
we estimate
What is the linear approximation for any generic linear function
Determine the necessary conditions such that the linear approximation function is constant. Use a graph to prove your result.
Explain why the linear approximation becomes less accurate as you increase the distance between
and
Use a graph to prove your argument.
When is the linear approximation exact?
The linear approximation exact when
is linear or constant.
For the following exercises, find the linear approximation
to
near
for the function.
[T]
[T]
[T]
[T]
[T]
[T]
For the following exercises, compute the values given within 0.01 by deciding on the appropriate
and
and evaluating
Check your answer using a calculator.
[T]
[T]
0.02
[T]
[T]
[T]
[T]
For the following exercises, determine the appropriate
and
and evaluate
Calculate the numerical error in the linear approximations that follow.
error,
error,
error,
For the following exercises, find the differential of the function.
For the following exercises, find the differential and evaluate for the given
and
For the following exercises, find the change in volume
or in surface area
if the sides of a cube change from 10 to 10.1.
if the sides of a cube change from
to
if the radius of a sphere changes from
by
if the radius of a sphere changes from
by
if a circular cylinder with
changes height from 3 cm to
if a circular cylinder of height 3 changes from
to
For the following exercises, use differentials to estimate the maximum and relative error when computing the surface area or volume.
A spherical golf ball is measured to have a radius of
with a possible measurement error of
What is the possible change in volume?
A pool has a rectangular base of 10 ft by 20 ft and a depth of 6 ft. What is the change in volume if you only fill it up to 5.5 ft?
ft3
An ice cream cone has height 4 in. and radius 1 in. If the cone is 0.1 in. thick, what is the difference between the volume of the cone, including the shell, and the volume of the ice cream you can fit inside the shell?
For the following exercises, confirm the approximations by using the linear approximation at
is an independent variable that can be assigned any nonzero real number; the differential
is defined to be
the equation
is the differential form of the derivative of
with respect to
is the linear approximation of
at
resulting from a measurement error dx
for a particular quantity,
is the relative error.
at
is defined using the equation of the tangent line, the linear approximation of
at
is also known as the tangent line approximation to
at

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1
Attribution: