Derivatives of Exponential and Logarithmic Functions

So far, we have learned how to differentiate a variety of functions, including trigonometric, inverse, and implicit functions. In this section, we explore derivatives of exponential and logarithmic functions. As we discussed in Introduction to Functions and Graphs, exponential functions play an important role in modeling population growth and the decay of radioactive materials. Logarithmic functions can help rescale large quantities and are particularly helpful for rewriting complicated expressions.

Derivative of the Exponential Function

Just as when we found the derivatives of other functions, we can find the derivatives of exponential and logarithmic functions using formulas. As we develop these formulas, we need to make certain basic assumptions. The proofs that these assumptions hold are beyond the scope of this course.

First of all, we begin with the assumption that the function $B\left(x\right)=b^x,b>0,$

is defined for every real number and is continuous. In previous courses, the values of exponential functions for all rational numbers were defined—beginning with the definition of $b^n,$

where $n$

is a positive integer—as the product of $b$

multiplied by itself $n$

times. Later, we defined $b^0=1,b^{\text{−}n}=\frac{1}{b^n},$

for a positive integer $n,$

and $b^{s\text{/}t}=(\sqrt[t]{b}{)}^s$

for positive integers $s$

and $t.$

These definitions leave open the question of the value of $b^r$

where $r$

is an arbitrary real number. By assuming the continuity of $B\left(x\right)=b^x,b>0,$

we may interpret $b^r$

as $\underset{x\to r}{\text{lim}}{b}^x$

where the values of $x$

as we take the limit are rational. For example, we may view $4^{\pi }$

as the number satisfying

As we see in the following table, $4^{\pi }\approx 77.88.$

We also assume that for $B\left(x\right)=b^x,b>0,$

the value $B^{\prime }\left(0\right)$

of the derivative exists. In this section, we show that by making this one additional assumption, it is possible to prove that the function $B\left(x\right)$

is differentiable everywhere.

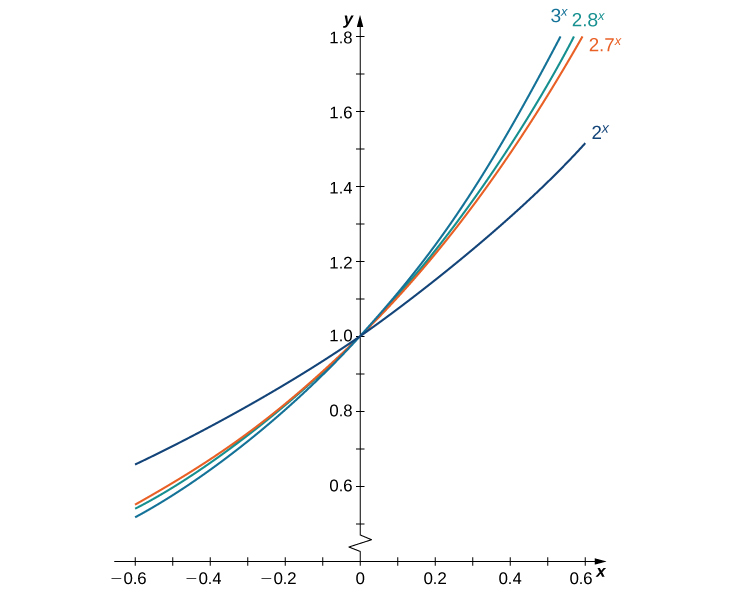
We make one final assumption: that there is a unique value of $b>0$

for which $B^{\prime }\left(0\right)=1.$

We define $e$

to be this unique value, as we did in Introduction to Functions and Graphs. [link] provides graphs of the functions $y=2^x,y=3^x,y={2.7}^x,$

and $y={2.8}^x.$

A visual estimate of the slopes of the tangent lines to these functions at 0 provides evidence that the value of e lies somewhere between 2.7 and 2.8. The function $E\left(x\right)=e^x$

is called the natural exponential function. Its inverse, $L\left(x\right)={\text{log}}_{e}x=\text{ln}x$

is called the natural logarithmic function.

For a better estimate of $e,$

we may construct a table of estimates of $B^{\prime }\left(0\right)$

for functions of the form $B\left(x\right)=b^x.$

Before doing this, recall that

for values of $x$

very close to zero. For our estimates, we choose $x=0.00001$

and $x=\mathrm{-0.00001}$

to obtain the estimate

See the following table.

The evidence from the table suggests that $2.7182<e<2.7183.$

The graph of $E\left(x\right)=e^x$

together with the line $y=x+1$

are shown in [link]. This line is tangent to the graph of $E\left(x\right)=e^x$

at $x=0.$

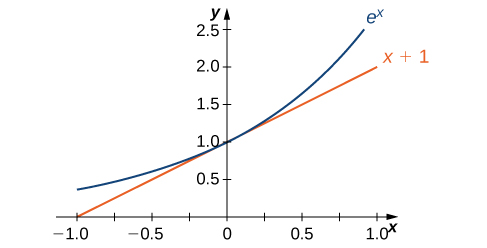
Now that we have laid out our basic assumptions, we begin our investigation by exploring the derivative of $B\left(x\right)=b^x,b>0.$

Recall that we have assumed that $B^{\prime }\left(0\right)$

exists. By applying the limit definition to the derivative we conclude that

Turning to $B^{\prime }\left(x\right),$

we obtain the following.

We see that on the basis of the assumption that $B\left(x\right)=b^x$

is differentiable at $0,B\left(x\right)$

is not only differentiable everywhere, but its derivative is

For $E\left(x\right)=e^x,E^{\prime }\left(0\right)=1.$

Thus, we have $E^{\prime }\left(x\right)=e^x.$

(The value of $B^{\prime }\left(0\right)$

for an arbitrary function of the form $B\left(x\right)=b^x,b>0,$

will be derived later.)

Derivative of the Logarithmic Function

Now that we have the derivative of the natural exponential function, we can use implicit differentiation to find the derivative of its inverse, the natural logarithmic function.

Proof

If $x>0$

and $y=\text{ln}x,$

then $e^y=x.$

Differentiating both sides of this equation results in the equation

Solving for $\frac{dy}{dx}$

yields

Finally, we substitute $x=e^y$

to obtain

We may also derive this result by applying the inverse function theorem, as follows. Since $y=g(x)=\text{ln}x$

is the inverse of $f\left(x\right)=e^x,$

by applying the inverse function theorem we have

Using this result and applying the chain rule to $h\left(x\right)=\text{ln}\left(g\left(x\right)\right)$

yields

□

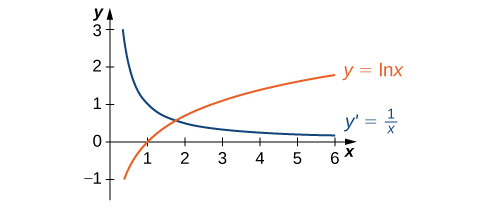
The graph of $y=\text{ln}x$

and its derivative $\frac{dy}{dx}=\frac{1}{x}$

are shown in [link].

Now that we can differentiate the natural logarithmic function, we can use this result to find the derivatives of $y=lo{g}_{b}x$

and $y=b^x$

for $b>0,b\ne 1.$

Proof

If $y={\text{log}}_{b}x,$

then $b^y=x.$

It follows that $\text{ln}\left(b^y\right)=\text{ln}x.$

Thus $y\text{ln}b=\text{ln}x.$

Solving for $y,$

we have $y=\frac{\text{ln}x}{\text{ln}b}.$

Differentiating and keeping in mind that $\text{ln}b$

is a constant, we see that

The derivative in [link] now follows from the chain rule.

If $y=b^x,$

then $\text{ln}y=x\text{ln}b.$

Using implicit differentiation, again keeping in mind that $\text{ln}b$

is constant, it follows that $\frac{1}{y}\frac{dy}{dx}=\text{ln}b.$

Solving for $\frac{dy}{dx}$

and substituting $y=b^x,$

we see that

The more general derivative ([link]) follows from the chain rule.

□

Logarithmic Differentiation

At this point, we can take derivatives of functions of the form $y={\left(g\left(x\right)\right)}^n$

for certain values of $n,$

as well as functions of the form $y=b^{g(x)},$

where $b>0$

and $b\ne 1.$

Unfortunately, we still do not know the derivatives of functions such as $y=x^x$

or $y=x^{\pi }.$

These functions require a technique called logarithmic differentiation, which allows us to differentiate any function of the form $h\left(x\right)=g{\left(x\right)}^{f(x)}.$

It can also be used to convert a very complex differentiation problem into a simpler one, such as finding the derivative of $y=\frac{x\sqrt{2x+1}}{e^x{\text{sin}}^{3}x}.$

We outline this technique in the following problem-solving strategy.

Key Concepts

• On the basis of the assumption that the exponential function $y=b^x,b>0$

  is continuous everywhere and differentiable at 0, this function is differentiable everywhere and there is a formula for its derivative.

• We can use a formula to find the derivative of $y=\text{ln}x,$

  and the relationship

  ${\text{log}}_{b}x=\frac{\text{ln}x}{\text{ln}b}$

  allows us to extend our differentiation formulas to include logarithms with arbitrary bases.

• Logarithmic differentiation allows us to differentiate functions of the form $y=g{(x)}^{f(x)}$

  or very complex functions by taking the natural logarithm of both sides and exploiting the properties of logarithms before differentiating.

Key Equations

• Derivative of the natural exponential function

  ---

  $\frac{d}{dx}\left(e^{g(x)}\right)=e^{g(x)}{g}^{\prime }\left(x\right)$
• Derivative of the natural logarithmic function

  ---

  $\frac{d}{dx}\left(\text{ln}g\left(x\right)\right)=\frac{1}{g(x)}{g}^{\prime }\left(x\right)$
• Derivative of the general exponential function

  ---

  $\frac{d}{dx}\left(b^{g\left(x\right)}\right)=b^{g(x)}{g}^{\prime }\left(x\right)\text{ln}b$
• Derivative of the general logarithmic function

  ---

  $\frac{d}{dx}\left({\text{log}}_{b}g\left(x\right)\right)=\frac{g^{\prime }\left(x\right)}{g\left(x\right)\text{ln}b}$

Chapter Review Exercises

True or False? Justify the answer with a proof or a counterexample.

Use the limit definition of the derivative to exactly evaluate the derivative.

Find the derivatives of the following functions.

Find the following derivatives of various orders.

Find the equation of the tangent line to the following equations at the specified point.

Draw the derivative for the following graphs.

The following questions concern the water level in Ocean City, New Jersey, in January, which can be approximated by $w\left(t\right)=1.9+2.9\text{cos}\left(\frac{\pi }{6}t\right),$

where t is measured in hours after midnight, and the height is measured in feet.

The following questions consider the wind speeds of Hurricane Katrina, which affected New Orleans, Louisiana, in August 2005. The data are displayed in a table.

You can also download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1

Attribution:

• For questions regarding this license, please contact partners@openstaxcollege.org.
• If you use this textbook as a bibliographic reference, then you should cite it as follows: OpenStax College, Calculus. OpenStax CNX. http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1.
• If you redistribute this textbook in a print format, then you must include on every physical page the following attribution: "Download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1."
• If you redistribute part of this textbook, then you must retain in every digital format page view (including but not limited to EPUB, PDF, and HTML) and on every physical printed page the following attribution: "Download for free at http://cnx.org/contents/9a1df55a-b167-4736-b5ad-15d996704270@5.1."